经历操作过程 抽象数学模型——人教版教材“表内除法”单元整体设计的教学实践研究

□李 芳 李露茜 邵汉民

人教版教材二年级下册“表内除法”分为两个教学单元，包含三个方面，分别是除法的含义、除法运算（用乘法口诀求商）和用除法运算解决问题。首先，从整体分析的视角，可以把这两个教学单元整合到一起进行梳理，从而发现其内在的编写结构。其次，从整体设计的视角，提出可以改进的地方。最后，把改进之处付诸实践，形成除法意义、除法运算与用除法运算解决问题相互融合的一个整体。

一、梳理——了解教材的编写特点

人教版教材在二年级下册第二、第四单元分别编排了“表内除法（一）”“表内除法（二）”，从整体分析，主要包括三个板块，第一个板块是“除法的初步认识”，第二个板块是“用2～6 的乘法口诀求商”，第三个板块是“用7～9的乘法口诀求商”。把两个教学单元的教学内容看成一个整体，主要包括三个方面的具体内容——除法的初步认识、除法运算（用乘法口诀求商）和用除法运算解决问题。笔者从教学内容与情境创设两个维度对教材进行梳理，以帮助教师理解教材编写的特点。

（一）单元学习层次清晰

从教材的编排结构看，三个方面的教学内容既相互独立，又层层推进。图1是教材编排的具体结构与对应的例题分布［注：带*的是表内除法（二）中的例题］。

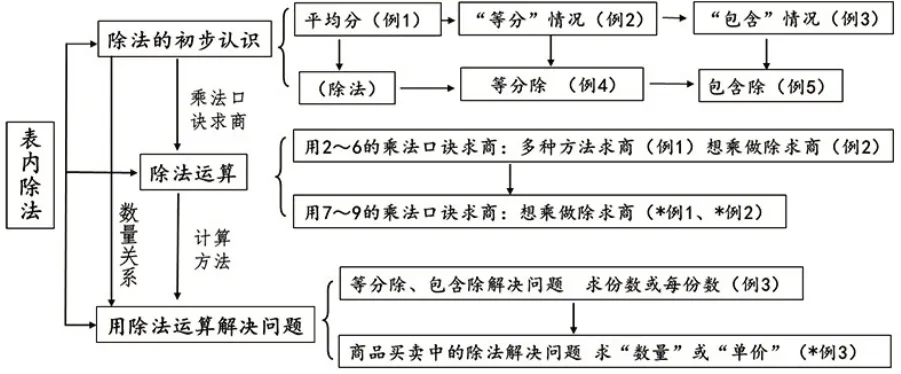
图1

从图1可以发现，“表内除法”三个方面的教学内容十分清晰，其中“除法的初步认识”是其他两个方面教学内容的基础。“用乘法口诀求商”是在“除法的初步认识”中的平均分物的基础上优化而成。“用除法运算解决问题”中的数量关系来源于“除法的初步认识”，而列式计算求商来源于“用乘法口诀求商”。

（二）联系实际创设情境

仔细分析教材中的例题，每一个例题都创设了贴近学生生活实际的情境，而“平均分物”又是它们共同的主题。第二单元“表内除法（一）”设计了“全班同学春游前，平均分零食”的主题图，具体用“分糖果”“平均分橘子”“平均分饼干”等情境作为例题来学习“平均分”概念。其中“平均分橘子”“平均分饼干”情境分别体现现实生活中两种平均分物的情况，即“等分（分配）”和“包含”，从而让学生充分地体会到“平均分”来源于现实生活。

除法可以看成对“平均分”过程和结果的记录。因此，教材中创设了“把12 个竹笋平均放在4 个盘里，每盘放（）个”和“20个竹笋，每4个放一盘，能放（）盘”两个问题情境。第一个问题情境属于平均分物的“等分（分配）”情况，第二个问题情境则是平均分物的“包含”情况。这样的问题情境编排分为四个层次：首先进行平均分的操作活动；接着用语言描述什么是平均分；然后用除法算式表示平均分的过程和结果；最后介绍除法算式中各部分的名称。

“用乘法口诀求商”的情境分成两类，一类是“数数”模型下的除法运算，另一类则是“矩阵”模型下的除法运算，用“一图式三算式（一个乘法算式、两个除法算式）”的方式进行呈现，即根据乘法与除法的关系，由一个乘法算式引出两个除法算式，并用乘法口诀推算除法的商。

两个单元中各有一个例题是“用除法运算解决问题”，每个例题的情境相对独立。第二单元“表内除法（一）”要解决的问题是“用笼屉放粽子”，第四单元“表内除法（二）”要解决的问题是商品买卖中求玩具的“单价”或“数量”。结合具体情境对问题进行抽象概括，形成解决此类问题的数量关系。

从“除法的初步认识”“用乘法口诀求商”和“用除法运算解决问题”这三个方面创设的情境中可知，它们的情境是相对独立的。“除法的初步认识”创设的主要是“平均分食物”这样的情境，便于采用实物或学具进行具体操作。“用乘法口诀求商”中，除了第二单元中的例1“猴妈妈分桃子”沿用之前的“平均分食物”的情境，其他的三个例题均采用“数数模型”或“矩阵模型”，先用乘法计算得到总数，再由乘法算式引出除法算式，最后用统一的乘法口诀计算出结果。“用除法运算解决问题”创设的两个情境“用笼屉放粽子”和“小朋友买玩具”，与前面的两个情境完全不同，这两个情境具有社会气息，更贴近日常的劳动与生活。

通过以上的单元梳理可以发现，整个“表内除法”教学内容的编排具有学习层次清晰、例题情境设计多样与不同学习内容情境独立等特点。这些特点既有值得在教学中充分展现的地方，也有可以改进之处。

二、反思——提出改进的具体内容

对于上述编排特点，笔者进行进一步反思，并发现问题，提出了一些可以改进的具体内容。

（一）发现割裂处

图1 的教材梳理结构图把教学内容清晰地划分为三个方面，它们既相对独立又密切联系。但是，教材在具体编排时，没能很好地体现出其中的联系。在“除法的初步认识”中，教材采用操作活动让学生学习“平均分”与“除法的含义”，却没有借机呈现除法算式中各部分的含义，并引导学生以此提炼出数量关系。或许编者认为不需要在此时引导学生学习另外两方面内容。

“用乘法口诀求商”实际上是依据除法是乘法的逆运算，利用表内乘法口诀求商，即“想乘做除”，从而实现除法运算与乘法运算的一致性。但是，仔细分析“用除法运算解决问题”的两个例题，在分析数量关系时，这两个例题并没有与相应的乘法解决问题进行关联，从而无法让学生感受到，除法解决问题的数量关系实质上是通过在乘法解决问题的数量关系中逆向思考所得的。也就是说，没有实现“用除法运算解决问题”与“用乘法运算解决问题”在数量关系上的结构化。

（二）实现一致性

从单元整体设计的视角，可以把“除法的初步认识”“用乘法口诀求商”与“用除法运算解决问题”进行整体构思，有机融合。具体而言，在“除法的初步认识”中，可以把“相同减数连减”与“除法运算”构建起联系，把“除法运算”当作“相同减数连减”的一种简便运算；然后在说明除法中各部分的含义时概括出除法算式表示的数量关系；计算除法的商则可以与乘法口诀相联系，最终实现除法的初步认识、除法运算的一致性。

图2中，从“分物情境”到“除法”的过程实际上也是用除法运算解决问题的过程。因此，把学习“除法含义”与用除法运算解决问题融为一体，可以更好地体现用除法运算解决问题中的“数量关系”与“除法含义”具有一致性。

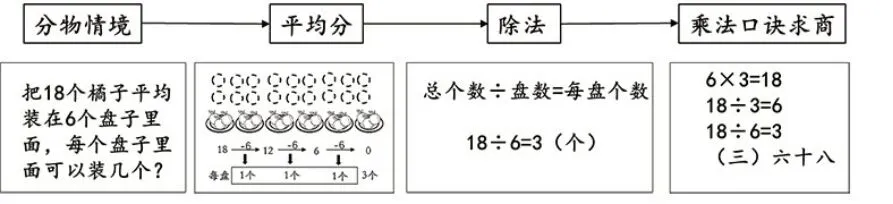
图2

（三）达成结构化

除法是乘法的逆运算，乘除法在内在结构上是相通的。因此，除法概念学习中的数量关系应与利用乘法口诀求商的除法运算相结合。在教学“用除法运算解决问题”时，可以让学生把学习的重点放在与二年级上册学习的用乘法运算解决问题构建联系上，形成用乘除法运算解决问题的基本结构。

如在第二单元的解决问题中，先创设用乘法解决问题的情境，让学生通过画一画（画出示意图）、列一列（列出数量关系）、算一算（列式解答算出结果）的方法解决问题（如图3）。再请学生观察图3中的已知信息与问题，并提出问题：能否通过交换其中的信息与问题，把它变成用除法运算解决问题？请学生自主改编，并按照用乘法解决问题的步骤自主解答。第四单元中的解决问题也可以采用同样的设计思路。

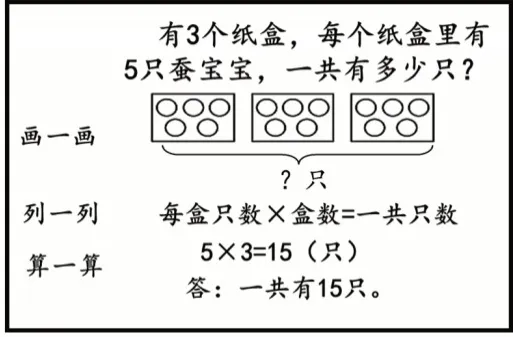
图3

基于以上思考，“除法的含义”与“用除法运算解决问题”从数量关系的视角实现了联通，“除法运算”与“乘法运算”通过乘法口诀发现了共同的计算方法，“用除法运算解决问题”与“用乘法运算解决问题”在数量关系上找到了联系，从而实现了“含义、方法、应用”这三者的有机融合。

三、实践——落实改进的教学思路

通过反思，笔者寻找到了在单元学习时可以改进的地方，即实现“除法的含义”“用乘法口诀求商”与“用除法运算解决问题”在情境创设、操作活动上的一致性，以及用乘法运算解决问题与用除法运算解决问题在数量关系上的结构化。那么，在实践中如何真正落实呢？我们需要进一步改进教学思路。

（一）“三者融合”学习含义

如何实现“除法的含义”“用乘法口诀求商”与“用除法运算解决问题”在情境创设、操作活动上的一致性？笔者以“用除法运算解决问题”为基本活动，让学生经历操作活动、连减记录与除法优化这样三个步骤，学习除法的含义。

教师先用板贴的形式出示6颗糖果，并提出要求：把它们分给三个同学，可以怎样分？学生操作后形成（1，1，4）（1，2，3）和（2，2，2）这样三种分法，比较后概括出分得“一样多”就是“平均分”。接着出示“平均分”中“等分”与“包含”两种情况的问题情境：（1）把18个橘子平均装在6个盘子里面，每个盘子里面可以装几个？（2）有18 个橘子，每个盘子装6 个，可以装这样的几盘？按照“分一分”“减一减”“数一数”这样三个步骤，学生发现“等分”中“分一分”时“每次取6个橘子”，是为了“每盘放一个”；而“包含”中“分一分”时“每次取6个橘子”，是为了“装一盘”。最后数出“每盘里面的个数”或者“装的盘数”，就可以得出结果（如图4）。

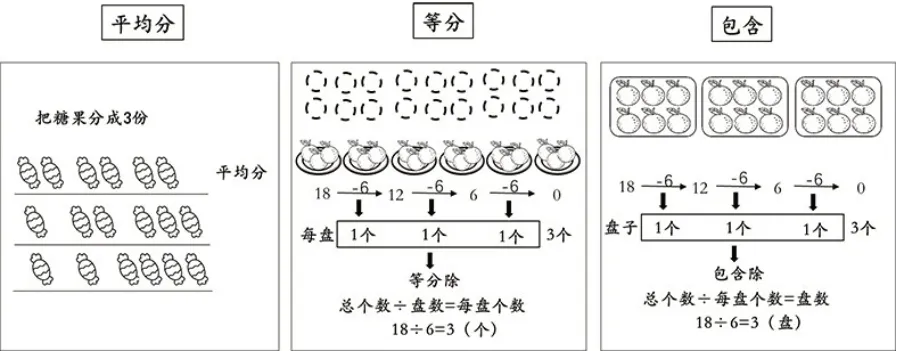
图4

显然，如果一直用“相同减数连减”的形式表示平均分，就会十分麻烦，尤其是分的次数增多时。因此，需要从“相同减数连减”的过程中提取出关键的数据，用新的运算符号进行连接，除法的记录以及数量关系就在这样的过程中逐步形成了。图4中的等分除与包含除就在这样的思路中产生。

（二）“想乘做除”学习计算

两个教学单元的标题都叫作“表内除法”，这里的“表”就是“乘法口诀表”，即用“乘法口诀”与乘除法的关系，推算出除法的商。这种思路在教学“除法”概念之一的“等分除”时已经让学生结合具体例子进行过尝试。即当学生利用“分一分”的方法求出“10÷2”和“10÷5”的结果后，让学生想一想，是否有办法不用画图“分一分”，也可以直接得到结果，学生自然地联想到二年级上册学习的表内乘法口诀——“二五一十”，推算出商。也就是从第2课时学习“除法的含义”时就开始让学生利用乘法口诀求商。

依照这样的教学思路，在第2课时“等分除”和第3课时“包含除”这两种除法含义的学习过程中，让学生结合除法各部分含义的学习，学习用“乘法口诀”进行计算。其中第2课时用到的乘法口诀是“2～6的乘法口诀”，第3课时用到的乘法口诀是“7～9的乘法口诀”。这样将除法的含义与除法的运算相融合，把用操作活动与连减得到结果优化为用“乘法口诀”推算出商，能够及时形成除法与乘法在运算中的内在联系。

（三）“由乘引除”解决问题

把两个教学单元整合成一个单元，并把解决问题的两个例题安排在前后连接的两个课时中，均由“用乘法运算解决问题”的数量关系引入。

如在“解决问题（2）”的教学中，先让学生依据信息提出问题，求出“总元数”（如图5）。那么，之后该如何“由乘引除”，用除法运算解决问题呢？从图5中的图式可以发现，还有每个皮球的价格这一个信息没有被利用，由此可以提出问题：（1）乐乐带的钱可以买多少个皮球？另外，每辆汽车的价格被乐乐挡住了，也可以在添加信息后作为问题提出；（2）乐乐带的钱可以买4辆汽车，每辆汽车多少元？在解决以上两个问题的过程中，概括出商品买卖中用除法运算解决问题的数量关系。

图5

上述教学把“除法”学习的三个方面有机融合，消除了三个方面的界线，从而让学生完整经历“除法”产生、形成、完善与应用的过程。

除法运算是四则运算的最后一种运算，教师在教学时可以充分利用学生已有的生活经验和知识基础。利用生活经验，安排具体的操作活动，让学生认识到“除法”中“平均分”的操作方法；利用知识基础，可以更好地把新知学习建立在已有旧知的基础上，探寻新旧知识之间的联系，形成内涵更加丰富的除法含义，让学生更好地体会除法与乘法的联系。