基于均分过程 构建除法模型——人教版教材二年级下册“等分除”教学实践研究

□李 君 汪秋霞 沈小青

在“平均分”教学中，用“相同减数连减”的形式表示“平均分”，可以直观地表示出平均分的过程，但是分得的结果却需要重新数一数。有时分的次数比较多时，书写记录会比较烦琐。为进一步提炼平均分的过程与结果，可以用“除法算式”对其进行优化，让学生借助“等分”的连减形式，概括出除法的“等分除”含义与表达形式。基于这样的思考，笔者进行了教学实践。

一、提炼含义，形成除法模型

当采用“相同减数连减”后“数出”结果的方法教学“平均分”时，已经有学生意识到可以用“除法算式”进行记录。顺着学生的思维，教师可以提出设想，形成除法模型。

（一）阅读审题，概括信息

教师用课件出示信息：熊猫要分竹笋，它想把24个竹笋平均放在4个盘子里（如图1）。要求学生阅读信息并进行解释。教师提问：“24指的是什么？4 又指的是什么？”引导学生解释“24”是竹笋的“总数”，“4”是盘子的数量。教师追问：“根据这些信息可以提出什么数学问题？”学生依据经验提出：平均每个盘子里放几个？

图1

上述信息与问题是根据教材“除法的初步认识”中的例4 改编的。原题中竹笋是“12 个”，现在改为“24 个”，主要是为了让学生感受有时用连减的形式记录平均分有一定的复杂性。

（二）连减操作，体会复杂

根据学生的学习经验，解决这个问题可以采用连减的形式。教师用课件演示平均分的过程，让学生用连减的形式进行记录，形成图2的解答过程。

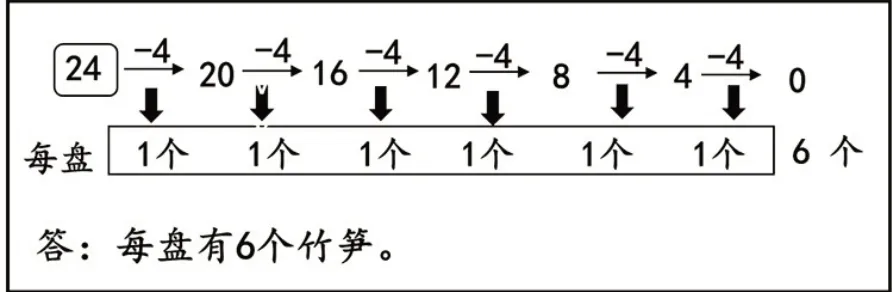
图2

用连减的形式记录平均分，可以直观地展示平均分的过程。但是，当平均分的次数较多时，记录起来就比较麻烦，这时就体现出用除法算式进行记录的必要性。

（三）优化模型，重构关系

教师引导学生观察连减过程，并提问：“哪些数特别重要？它们分别表示什么意思？”学生通过观察、思考，指出“24”表示总个数，“4”表示盘数，“6”表示每盘个数。教师根据学生的回答，顺势添上除号与等号，得到除法算式，与用连减的形式记录形成对应关系（如图3）。

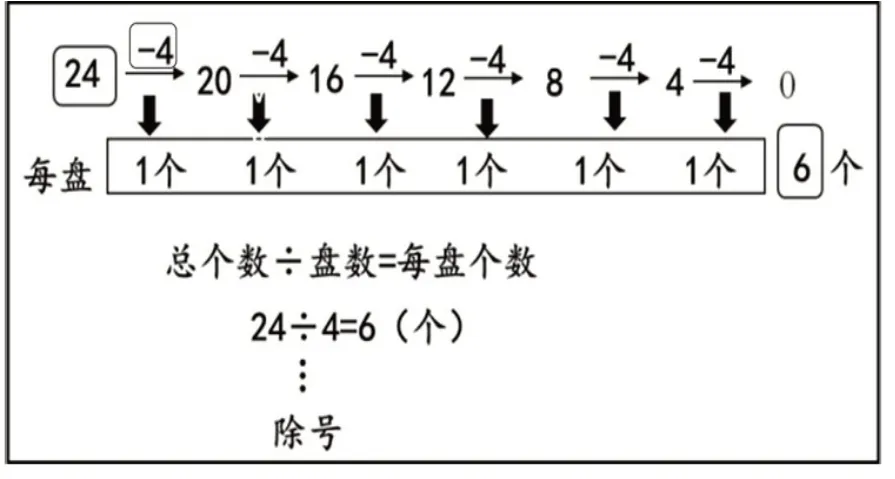
图3

教师用板书形式呈现出除法算式与数量关系后，请学生进一步说说每个数的含义，并示范相应的读法。最后概括出这个除法算式的含义：把24平均分成4份，每份是多少？

这样得到的除法算式，并不是一个简单的计算式子，而是对“平均分”操作过程的记录，更是对“相同减数连减”记录的优化。同时，依据具体情境说明除法算式各部分的名称，并列出数量关系，也使得除法算式中各部分的含义更具有现实意义。

二、结合例子，深化除法认识

相比于用连减的形式表示平均分的过程，用除法算式表示更加简捷。但是，因为这是新知，所以教师需要结合例子，让学生进一步明白除法算式中每一部分的含义。

（一）回顾旧知，丰富例子

教师依次出示学生学习平均分时的两个题目，以及相应的连减算式。请学生重新概括当中每个数的含义，提炼出数量关系，并用除法算式进行表示。

教师出示两个题目：（1）把18个橘子平均装在6个盘子里面，每个盘子里面可以装几个？（2）今天是三八妇女节，插花小队准备把24朵花平均分成8份，让小队的8 名成员带回家给妈妈，每位妈妈将收到多少朵花？

教师可以指出这是我们学习“平均分”时的两个问题，分别用连减的形式表示平均分的过程。教师依次出示图4、图5，让学生圈出重要的信息，然后模仿除法算式的表示形式，写出数量关系与除法算式（如图6）。

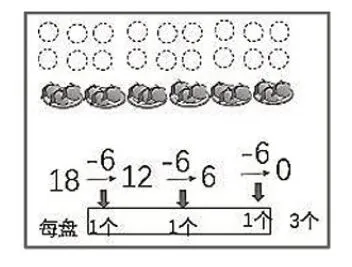
图4

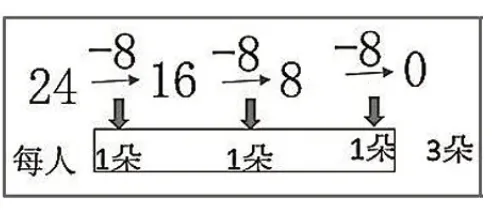
图5

图6

在“平均分”教学的基础上进行概括，既丰富了平均分的例子，也可以更好地体现用除法算式表示平均分的优势。

（二）比较归纳，提炼关系

很显然，以上三个平均分的问题都是“等分除”的问题，教师要让学生进一步观察图3 与图6 中的三个除法算式以及相应的数量关系，引导学生思考：这三个除法算式有什么相同的地方？形成“等分除”的一般数量关系：总数÷份数=每份数。同时，形成“等分除”的一般表示形式：把“总数”平均分成“若干份”，求“每份”是多少。进一步指出除法中的“总数”“份数”与“每份数”，分别叫作“被除数”“除数”“商”，像上面这样的形式就叫“等分除”。

把“等分除”作为除法学习的切入点，结合具体例子，从除法含义、数量关系与除法各部分的名称三个方面进行概括，可以让学生形成对除法的多层次认识。

（三）运用关系，解决问题

如何省略连减的表达，直接用除法表示平均分的过程？这要求学生结合题意，理解各个信息的含义，提炼出数量关系，再列式计算，最后画图验证。

教师出示题组：（1）有10根小棒，平均分成2份，每份有多少根？（2）有10根小棒，平均分成5份，每份有多少根？先请学生阅读题目，说一说两道题目中有什么相同点与不同点。学生指出这两道题目都要把10根小棒平均分，但是分成的份数不相同，且都可以用“总根数÷份数=每份根数”解决问题。再请学生依据列出的数量关系列式解答，最后用画小棒图的方式进行验证，形成如图7的解答过程。

教师通过回顾旧知与列举题组，让学生不断地积累由“等分”到“等分除”的记录过程，丰富“等分除”的例子，理解“等分除”的含义，概括出“等分除”的数量关系。

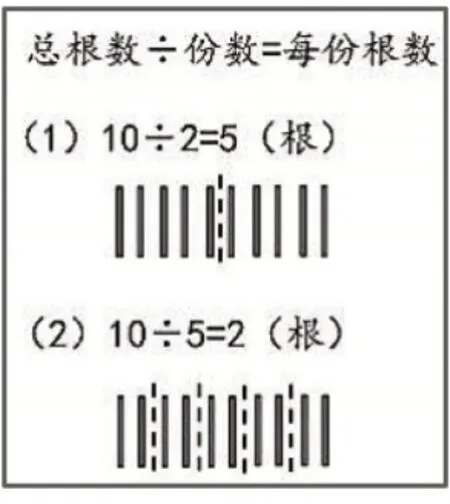
图7

三、分层练习，加深除法理解

从用连减形式表示平均分到用除法算式表示平均分，学生逐步理解了除法中“等分除”的含义。那么，如何计算除法的商？如何依据已知信息列出除法算式？如何依据除法算式编出相应的解决问题呢？这就需要设计相应的练习，加深学生对除法的理解。

（一）想乘做除，应用联系

教师让学生判断图7 中两个除法算式的商是否正确，提问：“有没有办法直接验证商是否正确？”学生思考后，运用乘法口诀“二五一十”进行验证。教师板书乘法口诀后，追问：“在这句乘法口诀中，积是除法中的什么？口诀中的乘数呢？”引导学生指出，乘法口诀中的“积”是除法中的“被除数”，“一个乘数”是除法中的“除数”，“另一个乘数”是除法中的“商”。利用这样的发现，让学生说一说，图3与图6 中的商分别可以利用哪一句口诀求出。学生回答后，教师出示如下的除法计算题，请学生边想口诀边填写结果：（1）30÷5=（）；（2）30÷6=（）；（3）36÷6=（）；（4）36÷（）=（）。其中第（4）题是开放题，学生体会到一句乘法口诀一般可以转化为两个除法算式，如“四九三十六”可以转化为“36÷4=9”“36÷9=4”。

（二）选择信息提出问题

解决“等分除”的问题，其基本结构是已知总数与份数，求每份数。但在具体情境中，三个量需要做到前后联系。为提升学生的审题能力，教师出示图8 中的三组问题，让学生先阅读审题，把有联系的信息与问题用线连接起来，再列式解答。

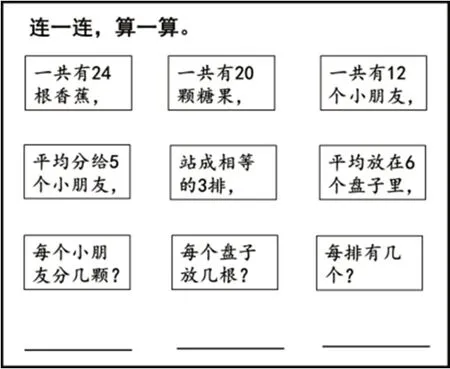
图8

（三）依据算式，自主编题

依据题目中的信息与问题，列出数量关系，再解决问题，是结合具体例子认识除法含义的过程。在此基础上，教师出示抽象的除法算式，让学生自主创设情境，自编相应的解决问题，经历由抽象的算式联想到具体的数量关系的过程。

例如“12÷3=4”是图8 中求每排有几个小朋友的除法算式，想一想，依据这一个算式，还可以解决怎样的问题？引导学生结合生活实际，根据例题的结构特征，模仿创编数学应用问题，体会算式的抽象性与数量关系的具体性。

在练习巩固阶段，通过有层次的专项练习，让学生形成“想乘算除”的除法运算意识，养成依据关键词分析信息与信息、信息与问题之间的联系，提炼数量关系，再列式解答的解决问题的习惯。

总之，从上述教学过程中可以发现，除法运算是平均分表达形式的优化。从运算意义上来讲，与减法特别是相同减数连减有密切的联系；就计算而言，又与乘法有联系。在本内容的教学中，除法含义的表达形式和各部分的名称，由连减形式的表达提炼而出；而除法的运算则让学生联系乘法口诀，用“想乘算除”的方法进行计算。由此，学生充分地体会到除法的产生建立在旧知的再认识与再利用的基础之上。