基于协同训练SVR 的脆性材料亚表面微裂纹深度预测

任闯　盛鑫　牛凤丽　朱永伟

关键词 脆性材料；亚表面损伤；支持向量回归；小样本；协同训练；粒子群优化支持向量回归

中图分类号 TG58; TG732 文献标志码 A

文章编号 1006-852X（2023）06-0704-08

DOI 码 10.13394/j.cnki.jgszz.2023.0006

收稿日期 2023-01-10 修回日期 2023-03-03

脆性材料的断裂韧性小，在固结磨料研磨阶段容易引入损伤[1]，尤其是其加工表面下的微裂纹。亚表面微裂纹的存在，不仅影响后续工序加工余量的确定，而且决定着工件的性能和服役寿命[2]。因此，准确检测研磨阶段引入的亚表面微裂纹深度有着重要的意义。

目前，常用的亚表面微裂纹检测方法有差动腐蚀法[3]、角度抛光法[4]、磁流变抛光斑点法[5] 等破坏性检测方法以及X 射线衍射法[6]、共聚焦激光扫描法[7] 等非破坏性检测方法2 类。但这2 类检测方法都存在一定的局限性[8]，破坏性检测方法容易引入新的损伤且操作烦琐， 非破坏性检测方法对设备的精密度要求较高等。

脆性材料的亚表面微裂纹深度是衡量其加工质量的重要指标，随着计算机技术的发展，研究人员将机器学习模型运用到脆性材料加工质量的预测中。机器学习模型立足于实验数据，如遗传算法优化的BP（backpropagation，BP）神经网络[9]、RBF（radial basis function，RBF） 神经网络[10]、支持向量回归（ support vector regression，SVR）[11] 等。上述模型的机器学习属于传统的监督学习，往往需要大量的标记数据，但现实环境中标记数据难以获取，限制了模型的学习能力；而半监督学习能利用标记数据以及未标记数据对模型进行训练和改进，进而提高模型的性能。在半监督学习的常用范式中[12-14]，以协同训练算法应用最为广泛。ZHOU 等[15]首次提出协同训练回归算法，给出了未标记数据的置信度评估方法， 并以KNN（ k-nearest neighbor， KNN）为学习器验证了算法的有效性；李东等[16] 采用奇偶分组的方法划分标记数据集，同时采用RPLS（recursivepartial least-square， RPLS） 和RBP（ recursive backpropagation， RBP） 2 种不同的学习器构建协同训练RPLS-RBP 混合回归模型，提高了其在非线性问题中的泛化能力。

目前，对协同训练回归算法应用的研究，大都建立在标记数据较为充足的基础上，而现有脆性材料固结磨料研磨下的亚表面微裂纹深度数据样本极少。因此，为提高脆性材料亚表面微裂纹深度的预测精度，以带有亚表面微裂纹深度的数据作为标记数据，提出一种针对小样本数据的协同训练SVR 模型。分析不同初始标记训练集划分方法对测试集均方误差的影响，并实验验证模型的泛化性能，以期证明所建模型可对不同脆性材料研磨产生的亚表面微裂纹深度进行较为准确的预测。

2 模型训练与评价

2.1 样本选择与模型训练

建立脆性材料亚表面微裂纹深度预测模型的前提是确定模型的输入参数、输出参数以及数据集。王建彬[19] 指出，影响脆性材料研磨加工特性的主要因素是材料的莫氏硬度、弹性模量以及断裂韧性。其次，在脆性材料研磨过程中，磨粒粒径以及研磨压力也对工件的亚表面损伤有着不可忽视的影响[20]。因此，将上述5 个因素作为模型的输入参数，研磨产生的亚表面微裂纹深度作为输出参数。训练与测试数据来源于课题组固结磨料研磨脆性材料实验[1-2， 4， 20-22]，涉及6 种典型的脆性材料，硬脆材料包括K9 玻璃、石英玻璃、镁铝尖晶石和蓝宝石，软脆材料包括铌酸锂和硫化锌。

亚表面微裂纹深度由角度抛光法测得，为贴近实际的应用场景，将实验所得亚表面微裂纹深度在1.00 μm以下的数据剔除掉，选出26 组标记数据。其中：表1为亚表面微裂纹深度训练样本集，包括21 组数据；表2为亚表面微裂纹深度测试样本集，包含5 组数据。未标记样本（即不包含亚表面微裂纹深度的研磨数据）集有38 组，部分未标记数据集如表3 所示。

协同训练需要先将训练集的标记数据分成具有差异性的2 组，并分别建立回归模型。传统的随机划分法并不适用于本文的小样本数据条件。因此，采取2种划分方法对表1 的标记数据集进行划分：一为分开划分法，根据脆性材料的莫氏硬度是否大于6.0 来划分，此方法可直观体现2 个训练集的差异；二为混合划分法，具体操作是将表1 的1～10 组作为标记数据集L1，11～21 组作为标记数据集L2，此方法可使2 个数据集均包含所有材料数据的全局信息。2 种方法均可划分出2 个具有差异的初始数据集，为后续协同训练算法的进行打下基础。

数据划分完成后，对模型进行训练。设置迭代次数为15 次，由于训练集数据在迭代过程中不断变化，因此以表2 的测试集数据在2 个学习器上的均方误差MSE 值为观察指标，得到MSE 随迭代次数的变化曲线图2。图2 表明：最初迭代时，2 种方法的2 个学习器在测试集中的MSE 值均有较大差别，这是由初始训练集的差异导致的；随着迭代进行，学习器1 的MSE 都是先急剧下降再趨于平缓，而学习器2 的MSE 则都是平缓下降再趋于平稳。说明2 种划分方法都可使模型在测试集的MSE 值减小，这是因为高置信度未标记样本的加入改善了其泛化性能。

图2 也表明了2 种划分方法的优劣：图2a 中2 个学习器最初的MSE 分别为5.79 和0.98，最终分别收敛于1.15 和0.35 附近；图2b 中2 个学习器最初的MSE 分别为4.02 和1.13，而最终分别收敛于2.00 和0.70 附近。这说明分开划分法下的2 个学习器虽然最初的预测结果相差较大，但最终的预测结果相差反而变小，且均能收敛至更小的MSE 值。这是因为分开划分法下的2 个初始训练集差异更大，建立的初始学习器差异更大，而这种差异有利于协同训练的进行，此结果与ZHOU 等[15]的理论一致。

MSE 和MAPE 值越小，说明模型的泛化能力越好，模型对测试集的预测越准确可靠。

2.3 预测结果及分析

为证明分开划分法下协同训练SVR 模型对小样本数据预测的先进性，选取监督学习PSO-SVR 模型作为對比，对表2 的测试样本集进行预测。图3 为2 种模型的预测误差，表4 为2 种模型的评价指标结果。

图3 直观表明协同训练SVR 模型预测的绝对百分比误差MAPE 最大值仅为19.49%，且误差浮动更稳定；而PSO-SVR 模型预测的绝对百分比误差最大值可达31.19%。表4 表明协同训练SVR 模型对测试集预测的MSE 和MAPE 值相比于PSO-SVR 模型的，分别减小了9% 和17%。因此，不论是对单个测试样本还是对整个测试集的预测，协同训练SVR 模型的预测结果更为可靠及稳定。

3 实验验证

以硬脆材料微晶玻璃（莫氏硬度为6.5）和软脆材料氟化钙（莫氏硬度为4.0）为研磨加工对象，用角度抛光法检测研磨后工件的亚表面微裂纹深度，并与协同训练SVR 模型的预测值对比。这2 种材料的莫氏硬度、弹性模量、断裂韧性参数组合在训练集中未被学习，因而可很好地证明模型的泛化性能。

3.1 研磨制样

2 种材料的验证样本集如表5 所示。其中， 1#与2#研磨压力不同，1#与3#磨粒粒径不同，2#与4#材料参数不同。微晶玻璃为中空的圆环形结构， 其外径为65.0 mm，内径为20.0 mm，厚为1.0 mm；氟化钙是直径为25.4 mm，厚为8.0 mm 的圆片。将相应粒径的金刚石固结于树脂基体中制成固结磨料垫，按照表5 设定的研磨压力，对2 种材料工件在ZDHP-30 平面精密环抛机上进行研磨实验。实验前先用油石修整磨料垫，使金刚石磨粒出露。研磨液为含有0.3% OP-10 乳化剂的水溶液，以提高磨料垫的湿润性。必要的研磨工艺参数见表6，表6 中参数相比于磨粒粒径及研磨压力，对研磨产生的亚表面微裂纹深度的影响较小[21]，可将其设为常用值。因氟化钙较软，因此其研磨时间应适量缩短。

3.2 亚表面微裂纹深度检测

采用角度抛光法对研磨后的工件进行亚表面微裂纹深度检测，角度抛光法的具体操作见文献[4]。角度抛光实验同样在ZDHP-30 平面精密环抛机上进行，具体抛光工艺参数见表7。

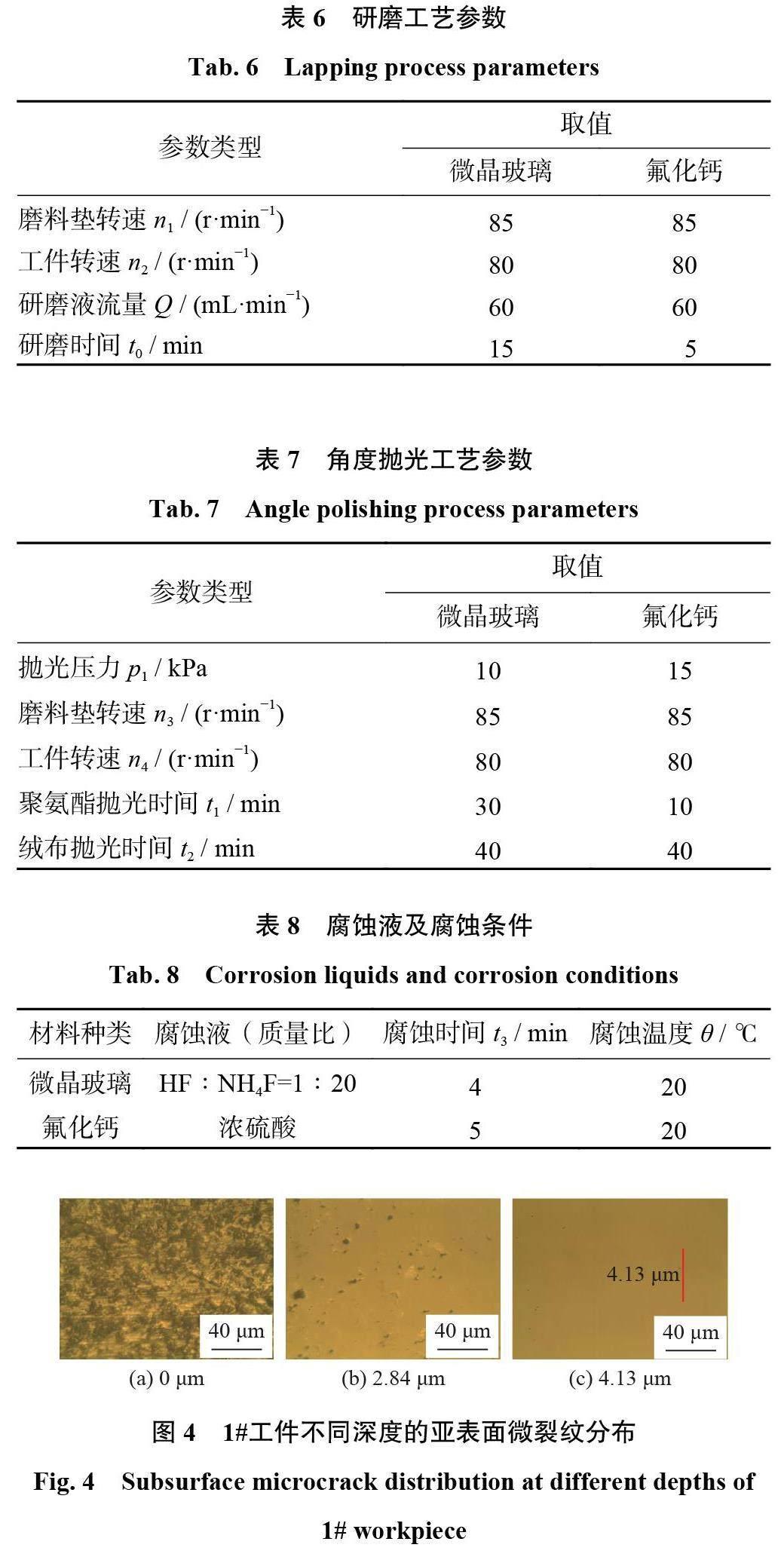
抛光后按照表8 的腐蚀条件对工件的抛光斜面进行腐蚀，使微裂纹清晰显现。腐蚀完成后，将工件充分清洗、干燥。用Leica DM1750M 金相显微镜观察微裂纹，结果如图4、图5 所示。图4 为实验1#工件不同深度下的亚表面微裂纹分布情况，图4a～图4b 随着深度增加，微裂纹减少，至图4c 中的红线左侧仍有少许微裂纹，而右侧为无损区，因此红线处为微裂纹消失终点，对应的深度值4.13 μm 即为亚表面微裂纹深度。图5为其余3 组的微裂纹消失终点，对应的亚表面微裂纹深度值分别为5.03、5.67 和5.89 μm。

3.3 检测结果与预测结果对比

验证样本集的亚表面微裂纹深度检测结果与协同训练SVR 模型预测结果对比如图6 所示，表明预测值与检测值存在一定的差距，预测误差在1.2%～13.8%，其平均值仅为7.7%，低于表4 测试集样本的平均预测误差值12.5%。此结果说明对于标记的训练数据集外的脆性材料种类，协同训练SVR 模型具有更好的容错与泛化性能，可根据材料参数准确预测其研磨加工产生的亚表面微裂纹深度，实现了建模目标。

4 结论

将现有的少许固结磨料研磨脆性材料亚表面微裂纹深度数据作为标记数据集，构建半监督的协同训练SVR 预测模型，并开展实验验证模型的泛化性能，得出如下结论：

（1）采用分开划分法和混合划分法对标记数据集进行划分，均可使协同训练SVR 模型在测试集的均方误差MSE 值减小；且分开划分法可使学习器收敛至更小的MSE 值，效果更优。

（2）协同训练SVR 模型预测的绝对百分比误差MAPE 最大值仅为19.49%。相比于监督学习PSO-SVR模型， 其在测试集的MSE 和MAPE 值分别减小了9%和17%，且预测误差更为稳定。

（3）以标记数据集中不包含的脆性材料微晶玻璃和氟化钙为实验对象，用角度抛光法检测其研磨后的亚表面微裂纹深度，检测值与模型预测值接近，预测误差在1.2%～13.8%，表明协同训练SVR 模型能对不同脆性材料研磨后的亚表面微裂纹深度进行较为准确稳定的预测。

作者简介

朱永伟，男，1967 年生，教授、博士生导师。主要研究方向：精密及超精密加工、表面工程等。

E-mail： meeywzhu@nuaa.edu.cn

（编辑：周万里）