二维MXene材料热输运性质的分子动力学模拟研究

汪鑫　安盟　陈海峰

摘要：MXene材料作为储能材料，在超级电容器中具有广泛的应用前景，其热传导和力学性能对超级电容器的性能和安全使用至关重要.本文利用分子动力学模拟研究了三种MXene材料的热输运和力学性质；还研究了二维MXene材料在工作过程中，其温度和形变对材料热导率的影响，并基于声子态密度探究了热导率变化的物理机制；同时，利用径向分布函数分析了不同应变下材料微观结构变化.研究表明，二维MXene材料热导率随着温度升高而降低，且应变越大热导率越低.本研究对MXene材料在超级电容器中的应用提供理论指导.

关键词：二维MXene材料; 分子动力学模拟； 热导率； 温度； 应变

中图分类号：TK124文献标志码： A

Study on molecular dynamics simulation of thermal transport

properties in two-dimensional MXene materials

WANG Xin， AN Meng CHEN Hai-feng（College of Mechanical and Electrical Engineering， Shaanxi University of Science & Technology， Xi′an 710021， China）

Abstract：MXene materials have promising application prospects as energy storage materials in supercapacitors，the heat conduction and mechanical properties of materials are very important for the performance and safety of supercapacitors.In this study，the thermal transport and mechanical properties of three kinds of MXene materials were studied by Molecular dynamics simulation; the effects of temperature and deformation on the thermal conductivity of two-dimensional MXene materials were also studied，the physical mechanism of the change of thermal conductivity was investigated based on the density of state of phonons; the microstructure of the materials under different strain was analyzed by Radial distribution function.The results show that the thermal conductivity of two-dimensional MXene materials decreases with the increase of temperature and decreases with the increase of strain.This study provides theoretical guidance for the application of MXene materials in supercapacitors.

Key words：two-dimensional MXene materials; molecular dynamics simulation; thermal conductivity; temperature; strain

0引言

2011年德雷塞爾大学Yury Gogotsi教授发现MXenes材料［1］.二维过渡金属碳化物、碳氮化物和氮化物由于其优异的性能，例如高本征电子和离子电导率、高比表面积以及丰富的氧化还原活性位点，被认为是储能领域非常有前景的新材料［2］.MXenes的通式为M_n+1X_nT_x（n=1-4），其中T_x表示源自合成过程的官能团［3］.二维MXene主要通过化学蚀刻MAX相中的A族元素（B、Al等）来制备，利用MAX相中A原子的弱结合力来选择性的去除A原子层，进而获得一种新型的二维纳米层状材料［4］.采用超声波等手段将多层MXenes剥落得到与石墨烯形貌相似的单层结构.Ti₃C₂T_x（T_x=-F，-O，-OH）是迄今为止报道最早且应用最广泛的二维MXene材料，研究发现这类材料也是水电解质中MXene层之间离子插层的合适材料［5］.作为电极材料在H₂SO₄电解质中的可以达到1 500 F·cm^-3的容量密度，实现高容量电容［6］.与传统的电极材料（包括过渡金属氧化物、导电聚合物和氧化还原活性有机分子）相比，MXene电极不仅具有良好的电容性，且具有更好的循环性，在超级电容器的应用具有广阔的前景［7］.

Xu等［8］将MXene作为电极材料利用分子动力学的方法研究电容器的循环稳定性以及电化学性质，但是对于电容器热传导问题没有进行一个深入的研究.然而，在电场的作用下超级电容器的电极电阻和介质会存在损耗，使得电容器发热，电容器内部温度升高，导致电容器的电化学性能发生变化.同时，长期受热会使介质加速老化，缩减电容器的寿命，严重时可造成为热击穿，致使电容器损坏，对相关设备的稳定运行有极大的影响.因此，对于电极材料热输运的研究就显得尤为重要.

经典分子动力学模拟方法已被广泛应用于研究二维材料热输运性质.在经典分子动力学模拟中，经验力场描述了原子间相互作用力.模拟体系中原子轨迹是通过求解牛顿运动方程获得.本文采用经典分子动力学模拟计算二维MXene材料的热导率和力学性质.研究了温度和应变对MXene材料热导率的影响规律及热输运机制.此外，本文还研究了不同MXene结构和应变率对力学性质的影响规律.本研究对于MXene基器件的热管理设计和应用具有重要意义［9］，同时也有助于理解二维材料结构对热输运的调控机制.

1模型与方法

1.1模型的建立

MXene是由MAX相刻蚀除去层间Al原子后得到的层状材料，本文构建了三种二维MXene结构材料（如图1所示），分别为Ti₂C、Ti₃C₂和Ti₄C₃ ［10］.模拟系统的宽度和长度分别为3.07 nm和 25 nm.其中第一性原理优化的单层Ti₃C₂厚度为0.8 nm［11］.

图1是三种单层MXene材料的分子结构，其中，蓝色实心球代表Ti原子，绿色实心球代表C原子.从图中可观察到，结构中Ti原子和C原子形成共价键Ti-C，且每个Ti原子与其周围四个C原子通过Ti-C共价键连接，形成有序的网状结构.实验制备的多层结构样品中通常存在残余应力，这些应力往往会影响MXene材料的导热性能.本文主要探究单层MXene材料，探究不同单层结构材料本征热导率，力争为设计不同需求MXene材料提供理论指导.

1.2模拟方法

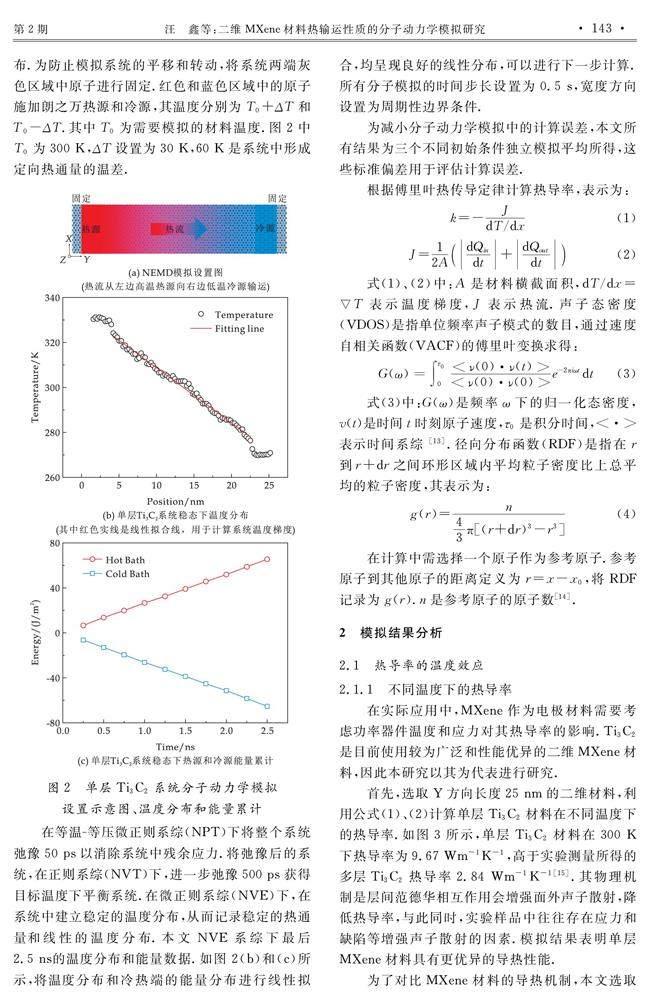
非平衡分子动力学（NEMD）模拟方法被广泛用于计算微纳米尺度和体块材料热导率［12］.本文基于NEMD方法计算三种不同结构的单层MXene热导率.本文选取经验力场MEAM来描述MXene中原子间相互作用力.如图2 （a）所示，系统的总长度为25 nm，沿着热流方向（Y方向）将系统均分为100个区域，用于统计记录系统温度分布.为防止模拟系统的平移和转动，将系统两端灰色区域中原子进行固定.红色和蓝色区域中的原子施加朗之万热源和冷源，其温度分别为T₀+ΔT和T₀-ΔT.其中T₀为需要模拟的材料温度.图2中T₀为300 K，ΔT设置为30 K，60 K是系统中形成定向热通量的温差.

在等温-等压微正则系综（NPT）下将整个系统弛豫50 ps以消除系统中残余应力.将弛豫后的系统，在正则系综（NVT）下，进一步弛豫500 ps获得目标温度下平衡系统.在微正则系综（NVE）下，在系统中建立稳定的温度分布，从而记录稳定的热通量和线性的温度分布.本文NVE系综下最后2.5 ns的温度分布和能量数据.如图2（b）和（c）所示，将温度分布和冷热端的能量分布进行线性拟合，均呈现良好的线性分布，可以进行下一步计算.所有分子模拟的时间步长设置为0.5 s，宽度方向设置为周期性边界条件.

为减小分子动力学模拟中的计算误差，本文所有结果为三个不同初始条件独立模拟平均所得，这些标准偏差用于评估计算误差.

根据傅里叶热传导定律计算热导率，表示为：

2模拟结果分析

2.1热导率的温度效应

2.1.1不同温度下的热导率

在实际应用中，MXene作为电极材料需要考虑功率器件温度和应力对其热导率的影响.Ti₃C₂是目前使用较为广泛和性能优异的二维MXene材料，因此本研究以其为代表进行研究.

首先，选取Y方向长度25 nm的二维材料，利用公式（1）、（2）计算单层Ti₃C₂材料在不同温度下的热导率.如图3所示，单层Ti₃C₂材料在300 K下热导率为9.67 Wm-1K^-1，高于实验测量所得的多层Ti₃C₂热导率2.84 Wm-1K^-1［15］.其物理机制是层间范德华相互作用会增强面外声子散射，降低热导率，与此同时，实验样品中往往存在应力和缺陷等增强声子散射的因素.模拟结果表明单层MXene材料具有更优异的导热性能.

为了对比MXene材料的导热机制，本文选取了其他两种MXene材料Ti₂C和Ti₄C₃.图3为三种MXene材料在200 K、300 K、400 K和500 K的热导率.三种材料热导率均随温度升高而降低，其主要原因温度升高，三声子散射强度不断增加，降低声子平均自由程，进而降低热导率［16］.Chen等［17］在二硫化钼纳米片和碳纳米管中也发现相似的变化趋势.相比之下，很容易发现Ti₃C₂在三种材料中表现出更加优越的导热性能.

2.1.2Ti₃C₂导热机制分析

如图4所示，利用公式（3）计算出温度为200 K（蓝色曲线）、300 K（绿色曲线）、400 K（橙色曲线）、500 K（红色曲线）下材料的VDOS并进行归一化处理，研究声子振动来探究温度变化是如何影响热导率.

VDOS的縱坐标对应的是参与振动的声子数目，横坐标代表声子在频域中的位置.通过晶格动力学可知，声子是热的载流子，在不同的频率位置参与振动，并将能量依次传递.MXene材料在低频部分存在大量且尖锐的峰，在高频部分也存在少量的峰.由此可知，大部分声子集中在低频区域进行振动，并且高频部分也存在一定数量的声子进行振动，热量输运过程中所有频率的声子都会通过振动参与热量的传递，只是低频部分的声子占据传热的主导地位.由图4可知，20 THz处声子频率随着温度的升高而降低，声子平均自由程也会减小.由热导率计算公式κ=1/3cvl可知，声子平均自由程的降低会导致热导率下降.

此外，整个频率范围内的峰值强度也随着温度的升高而降低.由图4可知，温度为200 K时蓝色曲线显示出更加尖锐的峰，500 K时红色曲线的峰值大幅下降.由于峰值强度的降低代表着声子参与振动的数目减少，所传递的热量也会随之下降，最终导致热导率的降低.

2.2应力應变

2.2.1材料的力学性能

由于MXene电极材料的工作温度是不断变化，材料的体积会随着温度的变化而改变，产生一定的应变，所以研究材料的应力-应变对其在实际中的应用有着重要的意义.应力-应变的方法已经被广泛使用在其他二维材料如石墨烯纳米片热导率调控中［18］.

本次研究在Y方向（初始长度为25 nm）引入的一个单轴拉伸的外力.图5是对二维MXene材料施加三种不同应变速率0.01 ps^-1、0.02 ps^-1、0.04 ps-1进行拉伸模拟，然后记录材料的应力应变.由图5可知，材料屈服点随着应变速率的增大而后移，最大应力也发生改变.影响屈服强度的外在因素有三种，分别是温度、应变速率、应力状态.本研究只改变材料拉伸的应变速率，保持温度和应力状态不变.当应变速率增大时，响应应变所需的时间就减短，这样就会使得应变更加局部化，因此整体材料发生应变就会需要更大的应力，所以会呈现出材料的屈服极限向后移动，最大应力增大的现象.

本文研究二维材料在弹性阶段热导率的变化.由图5可知，不同应变速率的拉伸对二维材料的弹性阶段（杨氏模量）没有明显的影响，所以后续的研究选取应变速率0.01 ps^-1进行计算，对整个材料热导率的变化结果不会产生明显的影响［19］.

如图6所示，对三种材料进行同一应变率下拉伸模拟.由图可知，Ti2C的杨氏模量最大，但是结合材料的热导率，得出Ti₃C₂的力学和热传导的综合性能相比于其他两种材料更加优越，杨氏模量的大小并不能直接影响热导率，结构的复杂性也对热导率有着一定的影响.

2.2.2应力应变对热导率的影响

为了进一步研究材料达到屈服极限之前的弹性形变范围内热导率的变化，固定拉伸速率0.01 ps-1，控制拉伸时间达到所需要计算的应变.本研究计算Ti₃C₂在0.02、0.04、0.06、0.08四种不同应变下材料的热导率，其结果如图7所示.由图可知，二维材料在不同应变下的热导率是随着应变的增加而减小.这是因为材料初始状态十分平整没有褶皱，不会出现在拉伸初期热导率增加的现象，反而是应力增大原子振动的幅度增大，增加声子非简谐性振动和声子的散射，导致热传导受限制.当应变达到0.08时，材料的热导率只有0.5 Wm-1K-1，通过插图观察材料在原始状态的均匀分布和应变为0.08时材料产生三处裂纹.材料表面的缺陷会增加声子散射，造成了材料热导率下降的结果.

为研究拉伸过程中材料的形态变化，利用公式（4）计算拉伸前后的径向分布函数图（RDF），其结果如图8所示.由图可知，MXene材料中Ti原子与最近的C原子之间的距离为2.25 ?，最近的Ti原子之间的距离和最近的C原子之间的距离相同，都为3 ?，并且在3.75 ?处发现第二个C原子，材料本身是有序排列，Ti原子与C原子之间的距离也是固定的.

图8为Ti₃C₂材料在无应变和应变为0.08时的RDF.峰值代表参考原子附近目标原子的出现的概率，材料应变达到0.08时全范围内峰值强度都在下降.因为材料本身是有一定的弹性，拉伸过后参考原子附近的目标原子数量变少，但是在第一峰值所在的位置没有明显的变化.在3.75 ?处第二个Ti-C峰的位置向右略微移动，Ti原子与第二位置C原子之间的距离增大，且较远距离处的峰逐渐变宽并趋于平缓.可以预测到当应变继续增大，远距离的峰开始将会逐渐消失，直至材料完全断裂后，峰值达到零点.

为进一步探究结构变化对热导率的影响，计算了单层Ti₃C₂材料在不同应变下的VDOS.如图9所示，材料拉伸前后的VDOS并且在全频率范围内的峰值强度都有所下降.由图可知，Ti原子的VDOS主要处在5 THz附近，很容易发现随着拉伸应变增大，Ti原子的峰值逐渐降低，表明在这个频率范围内参与传热的声子数目减少.C原子的VDOS主要处于高频范围（>14 THz）尤其是当应变达到0.08时多组尖锐的峰已经消失并逐渐趋于平缓，发现材料表面裂纹会声子振动从而影响热传递，导致热输运能力下降，相应的热导率也会减小.

3结论

（1）本文采用非平衡分子动力学方法研究了二维MXene材料的热输运性质，结果发现温度增加降低材料热导率，同时发现温度升高造成三声子散射，降低声子平均自由程，从而降低热导率.

（2）拉伸应变的模拟结果发现二维MXene材料在拉伸过程中表面发生一定的裂纹，基于RDF和VDOS分析了材料结构改变和热传导的改变机制.应力破坏了MXene材料晶体结构，出现更多的乱序结构，非简谐性声子增强，声子散射加剧，热导率降低.

（3）本研究将为二维MXene材料在功率器件的热管理设计和使用提供理论参考.

参考文献

［1］ Anasori B，Lukatskaya M R，Gogotsi Y.2D metal carbides and nitrides （MXenes） for energy storage［J］.Nature Reviews Materials，2017，2（2）：16 098.

［2］ Naguib M，Mochalin V N，Barsoum M W，et al.25 th anniversary article：MXenes：A new family of two-dimensional materials［J］.Adv.Mater.，2014，26（7）：992-1 005.

［3］ Shao H，Xu K，Wu Y C，et al.Unraveling the charge storage mechanism of Ti₃C₂Tx MXene electrode in acidic electrolyte［J］.ACS Energy Letters，2020，5（9）：287-380.

［4］ 鄭伟，孙正明，张培根，等.二维纳米材料MXene的研究进展［J］.材料导报，2017，31（5）：13-26.

［5］ 陈逸钊，刘存生.新型二维材料Ti₃C₂Tx的合成及其在电池中的应用研究进展［J］.功能材料，2022，53（9）：09 025-09 034.

［6］ Lukatskaya M R，Kota S，Lin Z，et al.Ultra-high-rate pseudocapacitive energy storage in two-dimensional transition metal carbides［J］.Nature Energy，2017，2（8）：17 105.

［7］ Lukatskaya M R，Mashtalir O，Ren C E，et al.Cation intercalation and high volumetric capacitance of two-dimensional titanium carbide［J］.Science，2013，341（6 153）：1 502-1 505.

［8］ Xu K，Merlet C，Lin Z，et al.Effects of functional groups and anion size on the charging mechanisms in layered electrode materials［J］.Energy Storage Materials，2020，33：460-469.

［9］ 时志强.新型微晶炭的结构与电化学电容特性［J］.物理化学学报，2008，24（2）：237-242.

［10］ Ibrahim Y，Mohamed A，Abdelgawad A M，et al.The recent advances in the mechanical properties of self-standing two-dimensional MXene-based nanostructures：Deep insights into the supercapacitor［J］.Nanomaterials （Basel），2020，10（10）：1 916.

［11］ H G.Effect of surface termination on the lattice thermal conductivity of monolayer Ti₃C₂Tz MXenes［J］.J.Appl.Phys.，2019，126：065 101.

［12］ Bao H，Chen J，Gu X，et al.A review of simulation methods in micro/nanoscale heat conduction［J］.ES Energy & Environment，2018，1：16-55.

［13］ Wan X，Demir B，An M，et al.Thermal conductivities and mechanical properties of epoxy resin as a function of the degree of cross-linking［J］.International Journal of Heat and Mass Transfer，2021，180：121 821.

［14］ Li S，Yu X，Bao H，et al.High thermal conductivity of bulk epoxy resin by bottom-Up parallel-linking and strain：A molecular dynamics study［J］.The Journal of Physical Chemistry C，2018，122（24）：13 140-131 407.

［15］ Chen L.Measurement and analysis of thermal conductivity of Ti（3）C（2）Tx MXene films［J］.Materials （Basel），2018，11（9）：1 701.

［16］ Wei Z，Yang J，Chen W，et al.Phonon mean free path of graphite along thec-axis［J］.Applied Physics Letters，2014，104（8）：081 903 .

［17］ Chen D，Chen H，Hu S，et al.Influence of atomic-scale defect on thermal conductivity of single-layer MoS2 sheet［J］.Journal of Alloys and Compounds，2020，831：154 875.

［18］ Li X，Maute K，Dunn M L，et al.Strain effects on the thermal conductivity of nanostructures［J］.Physical Review B，2010，81（24）：245 318.

［19］ S.Milad，Hatam Lee，Ali Rajabpour，et al.Mechanical behaviors of titanium nitride and carbide MXenes：A molecular dynamics study［J］.Applied Surface Science，2021，566：150.

【责任编辑：蒋亚儒】