波纹深度对波纹管气动噪声特性的影响

徐春龙 李皖

摘要 基于大涡模拟（large eddy simulation，LES）和FWH声比拟方法，仿真计算了波纹管气动噪声的三维模型，结果与理论值和实验测量相符合。对波纹深度进行了参数化计算分析，结果表明：①空气流过波纹管时，在波纹节点处绝对压力出现极大值，在波纹腹点处出现极小值;②随着轴向距离的增加，气动噪声的表面声压时均值增大;③随着波纹管波纹深度的增大，声压级和功率谱密度均值呈现先增大后减小的趋势。其数值计算方法对管道噪声处理有潜在应用价值。

关键词 大涡模拟；FWH声比拟方法；气动噪声

中图分类号：O422.8  DOI：10.16152/j.cnki.xdxbzr.2023-01-007

The influence of corrugation depth on aerodynamic noisecharacteristics of corrugated pipes

XU Chunlong1， LI Wan2

（1.College of Science， Changan University， Xian 710064，  China;

2.School of Electronics and Control Engineering， Changan University， Xian 710064， China）

Abstract Based on the method of LES （large eddy simulation） and FWH （Ffowcs Williams-Hawkings）， the aerodynamic noise of corrugated tubes in 3D model was simulated and calculated， which was consistent with the theoretical value and experimental value. Comparing the results of parametric calculation and analysis of corrugated depth， the research results show that： ① when the air flowing through corrugated tubes， the maximum of the absolute pressure appears at the corrugated pitch point and the minimum appears at the corrugated ventral point. ② The average of surface sound pressure of aerodynamic noise increases as the axial distance increasing. ③ The sound pressure level and the mean power spectral density first increase and then decrease as the corrugated depth increasing. The numerical calculation method in this paper has potential application value in the field of duct noise processing.

Keywords LES; FWH sound comparison method; aerodynamic noise

空氣以一定的速度流过波纹管时会产生湍流并发出响亮的声音，这种现象常见于通风系统内的管道、排水管道以及汽笛等［1-3］。波纹管气动噪声现象会导致较强的声压级和较高的噪声频率，对周围环境造成噪声污染，甚至会对管道设备带来安全隐患［4-7］。波纹管气动噪声研究是国内外研究者关注的热点。杨党国等人采用数值法探究了空腔自激振荡发声机理，得到了典型空腔模型的气动噪声特性［8］。孟令雅等人采用FWH声比拟法和边界元法，对管道噪声声源进行了数值计算［9］。Crawford研究了波纹管气动噪声的基频，提出了基于无摩擦流的波纹管气动噪声预测理论［10］。Nakamura等人实验测量了波纹管的声振荡现象，发现了波纹管气动噪声导致剪切层的不稳定性现象，从而导致了流声耦合系统的自激振荡现象［11］。王光学等人基于转捩模型和声比拟方法研究了圆柱噪声的产生机理［12］。根据前人研究可知，波纹管发声现象产生的机理尚不明确。

本文基于前人对波纹管不同几何结构内的流动及其导致的声学现象的研究，利用ANSYS Fluent软件，采用LES湍流模型和FWH声比拟方法，结合波纹管气动噪声理论和实验测量结果，对波纹管三维模型进行了气动噪声仿真计算，并研究了波纹管内流动特性和声学特性，对波纹深度进行了参数化仿真，探究了波纹管的结构和发声机理。

2 波纹管气动噪声实验与仿真计算

2.1 波纹管气动噪声实验

波纹管气动噪声实验测量使用的设备主要包括波纹管（AD16200mm）、AEROPRO1200W手提式鼓风机、TASCAM DR-40高保真数字录音机、AS-H8风速仪、VC824声级计、铁架台等，实验装置如图1所示。

实验测量中，将波纹管沿水平方向固定于铁架台上，保证其与台面平行，调节鼓风机风口平面与波纹管入口平面平行。启动鼓风机并缓慢调节风速，连续可调最高至25 m／s，当波纹管出现明显且稳定的波纹管噪声时，在测量点用录音机录音，每个频段重复测量3～5次，记录数据。对实验数据用Matlab自编程序进行傅里叶变换处理分析，得到波纹管气动噪声声压级频谱图与峰值频率。

2.2 建立波纹管三维模型

根据实验用波纹管的实际尺寸，建立波纹管几何模型，进行网格划分并清洗网格，建模模型如图2所示。其中：L为波纹管长度；h为波纹深度；r为波纹管管口半径；d1为波纹宽度，d2为波纹间距。设置波纹管及内部流体为计算域， 空气入口速度大小为20 m／s，方向沿Z轴正方向。设置时间步长Δt=0.000 01 s，先计算4 000步至稳定状态，开启FWH声学模块，再计算6 000步至0.1 s。设置监测点坐标时与实验测量位置坐标保持一致。

2.3 流场分析

对绝对压力沿Z轴方向进行分析，结果如图3A所示，表明沿Z轴方向上波纹管各点的绝对压力整体随距离的增加而降低，且在波纹节点处的绝对压力出现极大值，腹点处出现极小值，在管口第1个波纹节点处出现最大值。对空气流速沿Y轴方向的分布进行分析，结果如图3B所示，表明波纹管内速度场的分布由管径中心至管壁，速度呈现梯度分布，越靠近波纹管管壁速度越小。

波纹管三维模型下的速度场仿真结果如图4所示，可见空气沿波纹管流动过程中，在波纹腹点出现速度极大值，在波纹节点出现速度极小值。分析YOZ切面速度云图可知，在波纹管上游，空气流动较为稳定，而下游出现扰动和湍流，下游的扰动导致了波纹管气动噪声现象的产生。

2.4 声学分析

对波纹管声压脉动时均值分析结果如图5所示，可见表面声压脉动时均值随着沿Z轴方向距离的增大而逐渐增大，表明了波纹管气动噪声的声源域主要集中在下游区域［16-18］。

将实验测量结果用Matlab自编程序进行快速傅里叶变换，获得波纹管噪声频谱图，与模拟计算结果对比如图6A所示，对比结果显示声压级的实验值和数值计算值整体趋势基本一致，在100～5 500 kHz频段范围内，数值计算结果能较为准确地预测气动噪声的声压级。

波纹管气動噪声频率的理论预测值由Cumings模型及其共振频率公式给出，理论值、实验测量值以及数值计算值对比如图6B所示，f1～f11为噪声峰值频率。结果显示LES联合FWH数值计算结果较为准确。

2.5 波纹深度影响分析

基于以上的仿真计算方法，研究了波纹深度对波纹管气动噪声特性的影响。在空气流速一定条件下，选用不同波纹管的几何参数如表1所示。

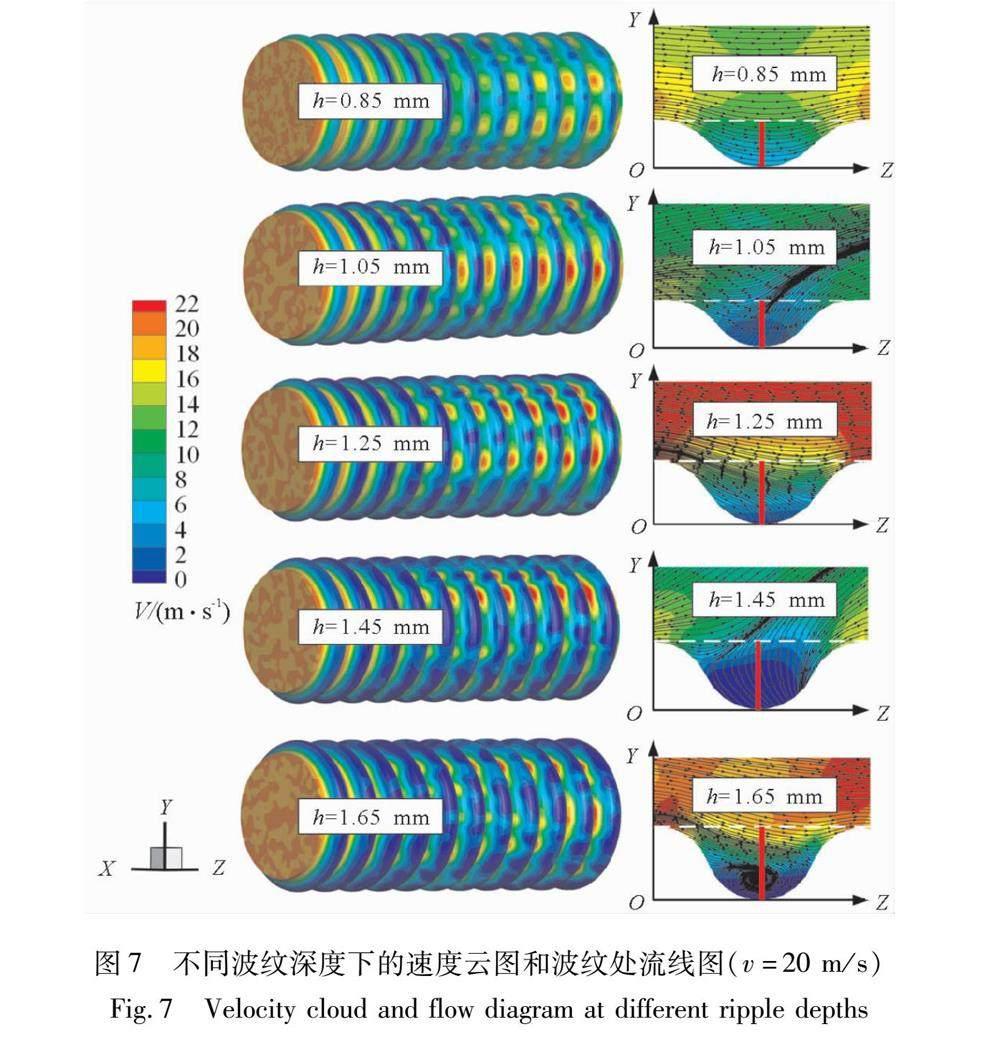
用LES联合FWH数值计算的方法对所选5种不同波纹深度的波纹管进行气动噪声分析。图7是在空气流速v=20 m/s时，改波纹深度得到的不同波纹管速度场分布情况。分析可知，当波纹深度较小时，波纹管上游区域几乎呈层流状态，在下游局部区域出现明显的扰动;当增大波纹深度时，下游区域处速度扰动增大;当波纹深度为1.25 mm时，波纹管下游扰动最为明显。通过放大观察波纹节点处的YOZ切面流线图可知，当波纹深度较小时，波纹节点处的空气呈层流状态，随着波纹深度的增大，波纹节点处的流逐渐紊乱，且逐渐产生旋涡。

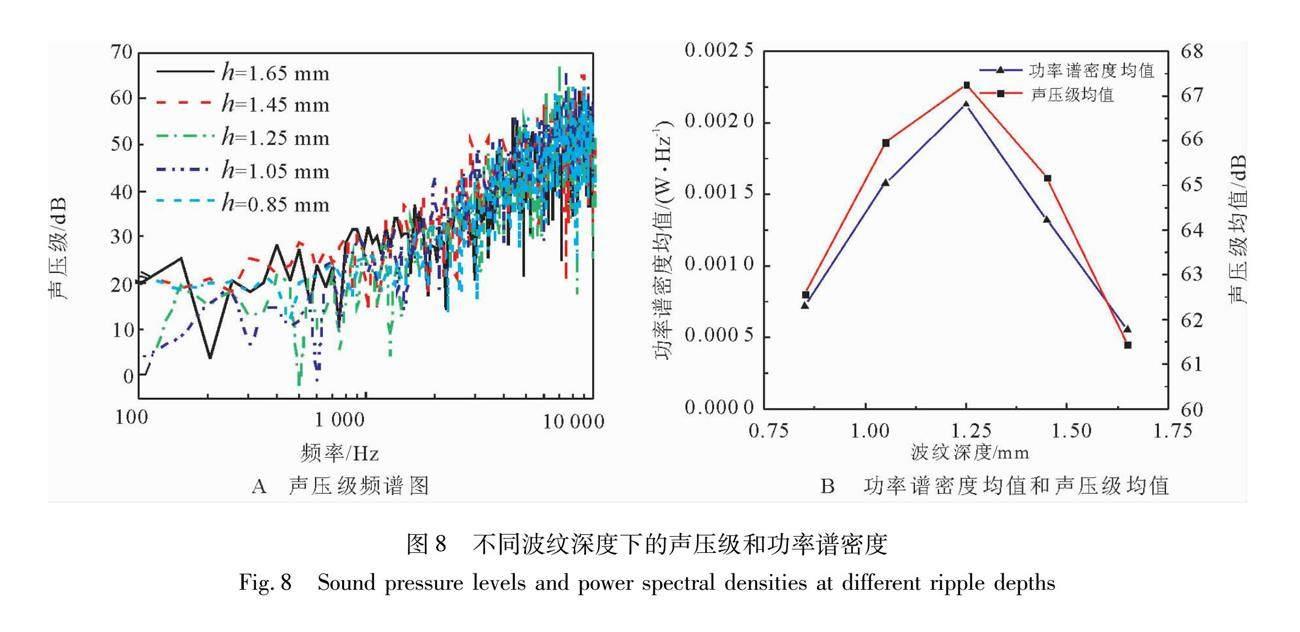
图8A是波纹深度对声压级频谱展开的影响，  随着深度的增大， 波纹管气动噪声的声压级频谱整体分布趋势一致。 图8B是波纹深度对功率谱密度和声压级均值的影响， 深度最小时， 波纹管的功率谱密度均值在0.000 75 W／Hz附近，声压级均值约为62.5 dB;深度增大，功率谱密度均值和声压级均值也随之增大;深度为1.25 mm时，功率谱密度均值超过0.002 W／Hz，增幅超过一倍，声压级均值约为67 dB;深度继续增大时，功率谱密度均值和声压级均值开始降低;深度为1.65 mm时，功率谱密度均值最低，为0.000 6 W／Hz，而声压级均值约为61.5 dB。

3 结语

本文使用LES湍流模型和FWH声比拟方法对波纹管三维模型进行了气动噪声仿真计算，验证了LES联合FHW声比拟方法的准确性和可行性。同时，对不同波纹管的波纹深度进行了参数化仿真计算，结果表明，波纹管气动噪声现象产生时，压力会在波纹处出现波动，绝对压力随轴向距离增大而逐渐降低，声源位于管壁下游区域，离出口端越近，表面声压时均值越大;随着波纹深度的增加，功率谱密度和声压级均值先增大后减小，在特定值出现最大值。本文使用的LES联合FHW数值仿真计算方法对工业领域中管道输运波纹管气动噪声具有参考意义。

参考文献

［1］ RAJAVEL B， PRASAD M G. Acoustics of corrugated pipes： A review［J］. Applied Mechanics Reviews，2013，65（5）：050801.

［2］ HUANG J Y， ZHANG K， LI H Y， et al. Numerical simulation of aerodynamic noise and noise reduction of range hood［J］. Applied Acoustics， 2021， 175（3）：107806.

［3］ CHEN B Q， WANG Y D. Active aerodynamic noise control research for supersonic aircraft cavity by nonlinear numerical simulation［J］.The International Journal of Electrical Engineering & Education， 2021：002072092199658.

［4］ GUO H， WANG Y S， ZHU F， et al. Multi-field coupling prediction for improving aeroacoustic performance of muffler based on LES and FWH acoustic analogy methods［J］. International Journal of Aeroacoustics， 2021，20（3/4）：414-436.

［5］ 郭玉婷，郝惠娣，吴煜斌，等.叶片型空穴射流清洗器结构的数值模拟研究［J］.西北大学学报（自然科学版），2016，46（4）：530-534.

GUO Y T， HAO H D， WU Y B， et al. Numerical simulation study on structure of blade-type cavitation jet cleaner［J］.Journal of Northwest University（Natural Science Edition）， 2016，46（4）：530-534.

［6］ 淡勇，刘晓东，袁娜.超高压管道有限元分析和强度评定［J］.西北大学学报（自然科学版），2007，37（3）：420-424.

DAN Y， LIU X D， YUAN N. Finite element analysis and strength evaluation of ultra-high-pressure pipeline［J］.Journal of Northwest University（Natural Science Edition）， 2007， 37（3）：420-424.

［7］ 刘昌华，殷海龙，白瑞峰，等.基于有限元与神经网络的含裂纹缺陷管道安全性分析［J］.西北大学学报（自然科学版），2021，51（4）：615-620.

LIU C H， YIN H L， BAI R F， et al. Safety analysis of pipeline with crack defects based on finite element and neural network［J］.Journal of Northwest University（Natural Science Edition）， 2021， 51（4）：615-620.

［8］ 杨党国，李建强，梁锦敏.基于CFD和气动声学理论的空腔自激振荡发声机理［J］.空气动力学学报，2010，28（6）：724-730.

YANG D G， LI J Q， LIANG J M. Cavity self-excited oscillation sound mechanism based on CFD and aeroacoustics theory［J］.Chinese Journal of Aerodynamics， 2010， 28（6）：724-730.

［9］ 孟令雅，劉翠伟，李玉星，等.输气管道气动噪声产生机制及其分析方法［J］.中国石油大学学报（自然科学版），2012，36（6）：128-136.

MENG L Y， LIU C W， LI Y X， et al. Mechanism and analysis method of aerodynamic noise generation of gas pipeline［J］.Journal of China University of Petroleum（Natural Science Edition）， 2012， 36（6）：128-136.

［10］CRAWFORD F S. Singing corrugated pipes［J］.The Journal of the Acoustical Society of America， 1975， 58（S1）：S2.

［11］NAKAMURA Y， FUKAMACHI N. Sound generation in corrugated tubes［J］. Fluid Dynamics Research， 1991， 7（5/6）：255-261.

［12］王光学， 王圣业， 葛明明，等. 基于转捩模型及声比拟方法的高精度圆柱分离涡/涡致噪声模拟［J］.物理学报， 2018， 67（19）：194701.

WANG G X， WANG S Y， GE M M， et al. High-precision cylindrical separation vortex/vortex noise simulation based on transfer model and acoustic analogy method［J］.Acta Physica Sinica， 2018， 67（19）：194701.

［13］MTAIS O. Large-eddy simulations of turbulence［M］.Berlin Heidelberg：Springer，2001.

［14］FFOWCS WILLIAMS J E，HAWKINGS D L. Sound generation by turbulence and surfaces in arbitrary motion［J］.Philosophical Transactions of the Royal Society of London Series A， Mathematical and Physical Sciences， 1969，264：321-342.

［15］孙晓峰，周盛.气动声学［M］.北京：国防工业出版社，1994：25-27，77-81.

［16］王畅畅， 王国玉， 黄彪，等. 可压缩空化流动空穴演化及压力脉动特性实验研究［J］.力学学报， 2019，51（5）： 1296-1309.

WANG C C， WANG G Y， HUANG B， et al. Experimental study on cavitation evolution and pressure pulsation characteristics of compressible cavitation flow［J］.Chinese Journal of Theoretical and Applied Mechanics， 2019，51（5）： 1296-1309.

［17］王巍， 张庆典， 唐滔，等. 射流对绕水翼云空化流动抑制机理研究［J］.力学学报， 2020，52（1）： 12-23.

WANG W， ZHANG Q D， TANG T， et al. Study on the suppression mechanism of jet cavitation flow around hydrofoil［J］.Chinese Journal of Theoretical and Applied Mechanics， 2020，52（1）： 12-23.

［18］马丽璇， 李恩义， 孙书霞，等. 跨声速空腔声学特性数值模拟［J］.中国民航大学学报， 2020， 38（5）： 10-16.

MA L X， LI E Y， SUN S X， et al. Numerical simulation of acoustic characteristics of transsonic cavity［J］.Journal of Civil Aviation University of China， 2020， 38（5）： 10-16.

（编 辑 李 静）