基于LED的光量子理论测量普朗克常量陈霞

孙太宇 何宇飞 林凡宸 梁晓森 冯列峰

摘 要 普朗克常量在物理学中具有非常重要的意义，可根据LED的光量子理论，对普朗克常量进行测量。LED是一种常见的半导体器件，其电学特性和光学特性容易受到温度的影响。本文利用自制的可调恒温器对LED进行控温，测量了不同温度下LED的阈值电压和峰值波长。实验表明，随着LED温度的升高，其阈值电压降低，同时峰值波长红移。基于光量子理论，进一步对LED的阈值电压和峰值波长进行数据处理，将阈值电压和频率做直线拟合，从拟合直线的斜率得到普朗克常量。

关键词 普朗克常量;发光二极管;伏安特性;峰值波长

普朗克常量是物理学中极其重要的一个常量，它是联系物质的粒子性与波动性的重要参数，是量子世界和可观测量子效应的基本标志。它的精确测定对于质量计量的物理基准建立、量子效应精密测量及早期宇宙大爆炸物理特性研究等都有重要意义[1]。特别是在第26届国际计量大会上，基于普朗克常量重新定义了质量的单位千克，标志着国际单位制全面进入量子化时代[2]。测量普朗克常量的方法主要有：光电效应方法[3]，根据爱因斯坦光电效应方程，通过测量截止电压和入射光频率之间的线性关系来计算普朗克常量;黑体辐射方法[4]，根据黑体辐射强度的频率分布，进行分析后可通过玻耳兹曼常数计算得出普朗克常量;玻尔理论方法[5]，根据玻尔的氢原子理论，通过测量原子跃迁时辐射出光子的波长，并确定光子跃迁前后的能级，即可得出普朗克常量。此外还有：量子霍尔效应方法[6]、基布尔秤测量方法[7]、电压天平测量方法[8]等。其中，利用光电效应测量普朗克常量是大学物理实验中非常经典的方法。但是，光电管中的暗电流等因素会对测量结果产生影响。在文献[9]和文献[10]中，提出了基于LED的伏安特性及光谱特性测量普朗克常量的方法。该方法采用单色LED，元器件容易获得，价格低廉，操作简单方便。通过测量LED 的阈值电压和峰值波长，得到普朗克常量。但是结果表明，在LED 发光发热的过程中，会导致阈值电压和峰值波长的漂移，造成普朗克常量的测量结果误差较大。这是因为LED 属于电致发光器件，与传统光源的发光原理不同，传统光源通过辐射散热，但是LED 不能通过这种方式散热，从而导致器件温度容易升高，严重影响LED 的光通量、寿命以及可靠性，因此采用LED 测量普朗克常量时，考虑温升的影响有着重要的实际意义。

本文中，利用自制的可调恒温器，将不同颜色LED器件封闭其中，在充分考虑温升效应后，详细测量了LED的伏安特性以及光谱特性，并通过对数据拟合，精确计算出了普朗克常量。

1 实验原理和装置

发光二极管的核心是PN 结，由含有镓、砷等物质的材料制成，是一种非线性元器件，其伏安特性与一般的二极管相似。当对LED 外加反向电压时，只有微安量级的反向电流;当反向电压超过击穿电压时，LED被击穿损坏。当LED的外加正向电压低于阈值电压时，LED 不导通，几乎没有电流，也不发光;当LED 的外加正向电压高于阈值电压时，LED 内的电子和空穴复合，同时以辐射光量子的形式释放能量。

根据LED 的光量子理论，电子和空穴复合时，电场力对电子做的功W =eUth，辐射出的光量子的能量E=hν，在不计能量损失的情况下，电场力对电子做的功全部转化为光量子的能量W =E，由此可得hν=eUth，即h=eUth/ν，其中，e 为电子的电荷量，Uth 为LED的阈值电压，h 为普朗克常量，ν 是光量子的频率。再根据光速c 和波长λ、频率ν 的关系c=λν，可得普朗克常量的计算公式为

由此可见，精确测量出LED 的阈值电压Uth和波长λ 是计算普朗克常量h 的关键。但值得注意的是，温度变化会影响LED的伏安特性、波长、光通量、照度、寿命以及可靠性等。在电流一定时，温度越高，LED 的电压越低。此外，温度升高还会导致LED 发光红移。这些都会影响普朗克常量测量结果的准确性。因此，对于实际工作中的LED器件，必须考虑温度对器件电学和光学特性的影响。测量不同温度下，LED 的阈值电压和峰值波长，得出阈值电压和发光频率的线性关系，从拟合直线的斜率计算出普朗克常量。

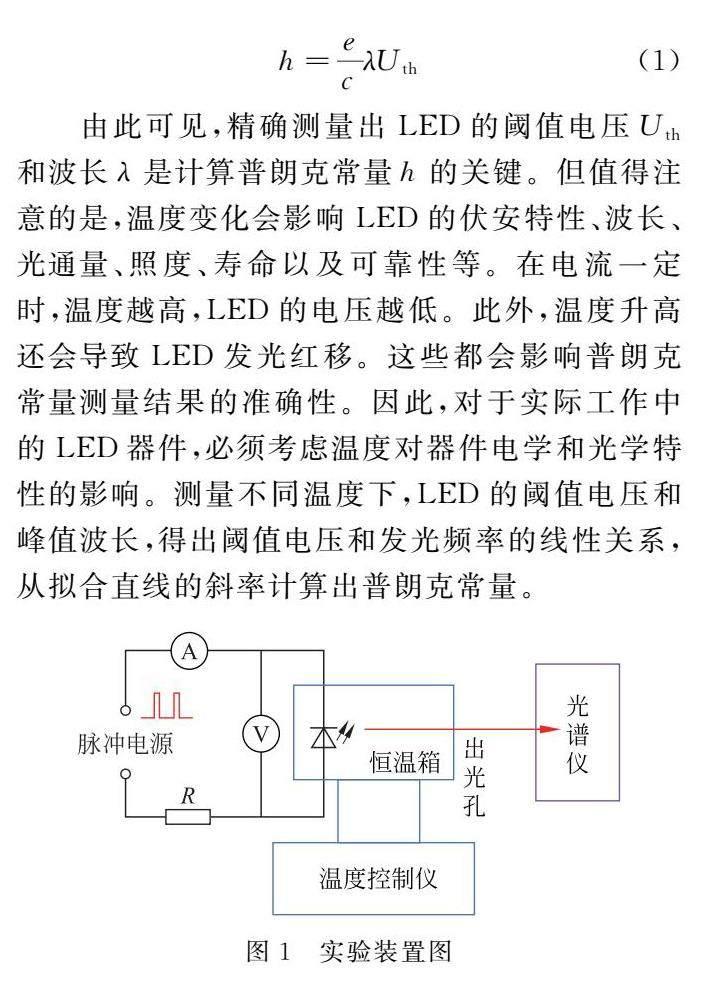
采用单色LED、利利普 AG1022 信号发生器、固纬GDM-8341数字万用表、港东WGD-5型多功能光栅光谱仪、自制可调恒温器搭建普朗克常量测量装置，如图1所示。实验中选用1W 的LED灯珠，蓝光LED的工作电压约为3V，额定电流约为350mA;红光LED的工作电压约为2V，额定电流约为350mA。选用脉冲电源，在较小占空比的脉冲直流驱动下，LED芯片温度无法升高且近似等于温控室温度[11]。在测量过程中，LED始终置于恒温箱内。将LED的正向电压由零开始缓慢增大，记录相应的电压和电流，可得到不同温度下的LED伏安特性曲线。在伏安特性测量电路中，选用数字万用表的直流电压5V 挡，分辨率为0.1mV;直流电流500mA 挡，分辨率为0.01mA。光栅光谱仪的波长扫描范围为200.0～800.0nm，扫描间隔0.1nm。在不同温度下测出LED的峰值波长。

本实验的控温装置是利用废旧仪器改造而成的。利用固体导热系数测量仪，设计制作可调恒温器。将实验室淘汰报废的老旧设备进行改造，用于物理实验是非常有意义的。随着科学技术的不断发展，有的仪器设备因性能不良或产品更新换代而被淘汰，有的仪器设备因年久失修零件老化、到了使用的年限而报废。在教学型实验室中，这些淘汰或报废的仪器数量随着经济社会的发展逐年增多。虽然这类仪器设备被淘汰或报废，但它们在实验教学中仍有余热可以发挥，充分利用这些废旧仪器设备，能够在培养学生的创新精神和创新能力方面起到很大的作用。

固体导热系数测量仪，因仪器达到使用年限，设备老化性能不良，且已有新型智能产品对其更新换代而被淘汰。虽然该仪器已经不能完成原来的实验教学任务，但是仪器中的加热装置仍然是可以使用的。对该设备中的加热装置进行再利用，增加了定制的亚克力板和保温盒，自制了可调恒温器。自制可调恒温器包括上下两部分，上方恒温箱，下方温度控制仪。被测LED置于上方恒温箱内，恒温箱内放置温度传感器，通过下方的温度控制儀进行调控，实现恒温条件。在恒温箱侧壁开一小孔，可以通过小孔观察LED 的发光情况，也可以通过小孔透出的光，用光栅光谱仪测量LED的波长。温度控制仪位于恒温箱下方，由定制的亚克力板作为仪器盒，内部置有加热电源、温差电偶等元件，仪器盒正面的面板设置数字温度显示屏。改造完成的自制可调恒温器如图2所示，控温方式为铂电阻温度传感器PID控温，控温区间为室温约110.0℃，控温精度为0.1℃。

2 实验结果分析

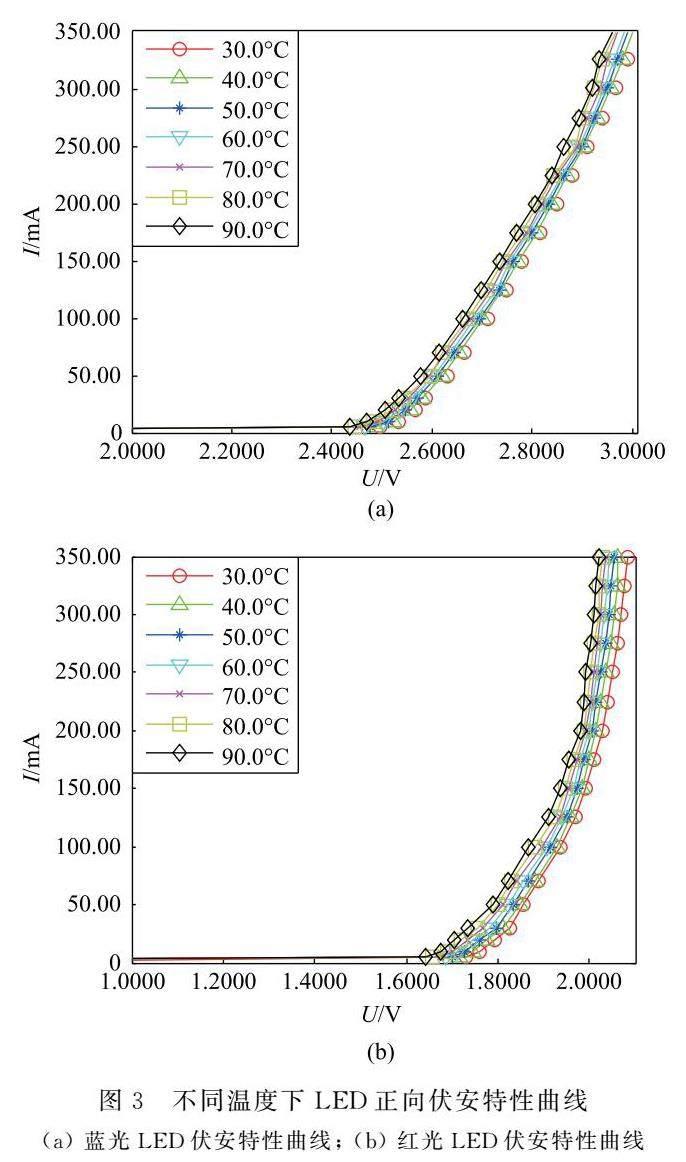
在本实验中，将LED置于自制可调恒温器内控制温度，测量LED正向伏安特性。为便于分析，本文以10.0℃为间隔，测量了从30.0～90.0℃范围内LED的电流和电压，绘制出各温度下的伏安特性曲线簇。图3（a）是蓝光LED 在不同温度下的伏安特性曲线。同样的方法，测量了红光LED从30.0～90.0℃范围内的电流和电压，绘制出各温度下的伏安特性曲线簇。图3（b）是红光LED在不同温度下的伏安特性曲线。

从图中可以看出，LED 的伏安特性曲线随着温度的升高而向低压偏移，说明阈值电压降低。在不同电流下的电压随温度升高而减小的幅度有所不同，当电流比较小时，电压随温度升高而减小的幅度较小，当电流比较大时，电压随温度升高而减小的幅度较大。这是因为，当LED导通后正常发光时其内阻几乎可以忽略不计，并且I-U 数据具有良好的线性关系，因此利用这段工作区的曲线变化趋势可以确定LED正向导通的阈值电压。

选取LED 伏安曲线工作区的电流和电压数据进行直线拟合，拟合出的直线与横轴的交点即为阈值电压。以蓝光LED 在温度为30.0℃时的伏安特性曲线为例，如图4所示。选取电流I≥200.00mA 的数据点，对其进行直线拟合，拟合出的直线与横轴的交点即为阈值电压。同样的方法，选取温度为40.0～90.0℃时蓝光LED伏安曲线工作区的电流和电压的数据，分别进行直线拟合，求出相应温度下的阈值电压。表1 给出了30.0～90.0℃蓝光LED 的阈值电压。图5（a）给出蓝光LED 阈值电压随温度的变化曲线。从图中可以看出，随着温度的升高，LED 的阈值电压逐渐降低。

用光栅光谱仪测量LED的峰值波长。将蓝光LED置于自制可调恒温器内，控制温度为30.0℃，通过恒温箱侧壁的出光孔，观察LED 的发光情况，用光栅光谱仪进行波长扫描，测量出蓝光LED在30.0℃ 时的峰值波长。同样的方法，可得到40.0～90.0℃时蓝光LED 的峰值波长。表1给出了30.0～90.0℃ 时蓝光LED 的峰值波长。图5（b）给出蓝光LED 峰值波长随温度的变化曲线。从图中可以看出，随着温度的升高，LED 的峰值波长发生红移。

进一步，选取不同温度下红光LED伏安曲线工作区的电流和电压的数据，分别进行直线拟合， 求出相应温度下的阈值电压。表1给出了30.0～90.0℃红光LED 的阈值电压。图5（a）给出红光LED阈值电压随温度的变化曲线。从图中可以看出，红光LED的阈值电压随着温度的升高逐渐降低。用光栅光谱仪测量不同温度下红光LED的峰值波长。

表1给出了30.0～90.0℃红光LED 的峰值波长。图5（b）给出了红光LED 峰值波长随温度的变化曲线。从图中可以看出，红光LED的峰值波长随着温度的升高发生红移。

根据测量得到的不同温度下的阈值电压，以及不同温度下的峰值波长，将相同温度下的阈值电压和峰值波长一一对应起来。并将波长、频率和光速的关系ν=c/λ，代入公式（1），可得阈值电压和频率呈线性关系，其表达式为

将阈值电压Uth 和频率ν 拟合直线，直线的斜率为k=h/e，即可得出普朗克常量h=ke。图6（a）和图6（b）分别给出蓝光LED和红光LED阈值电压Uth 和频率ν 拟合的直线。蓝光LED和红光LED直线斜率分别为4.0884×10-15 V/Hz和4.0858×10-15 V/Hz，计算得到的普朗克常量h 的值分别为6.541×10-34 J·s和6.537×10-34 J·s。當置信概率为95%时，用蓝光LED和红光LED测量得到的普朗克常量h 的不确定度分别为0.002×10-34 J·s和0.003×10-34 J·s，测量结果可以分别表示为h蓝=（6.541±0.002）×10-34 J·s和h红=（6.537±0.003）×10-34J·s。普朗克常量的公认值为h0= 6.626×10-34 J·s，可以看出，本文所采用的方法，考虑了温度对LED器件的影响，得到的测量结果接近理论值。

3 结语

基于LED的光量子理论测量了普朗克常量，考虑温度的变化会造成LED 的阈值电压和峰值波长漂移，通过测量不同温度下LED的伏安特性曲线，得出了阈值电压随温度的变化曲线，以及峰值波长随温度的变化曲线。结果表明，随着温度的升高，LED 的阈值电压降低，同时峰值波长红移。对LED在不同温度下的阈值电压和频率拟合直线，从拟合直线的斜率精确得到了普朗克常量。结果表明，考虑温升对LED的阈值电压和峰值波长的影响，可使普朗克常量的计算结果更加准确。

但 值得注意的是，实验中LED的电能并没有完全转化为光能，总会有部分热能产生，测量也存在着一定的误差。

参 考 文 献

[1] 邓崇林. 以量纲分析重新发现普朗克公式[J].物理与工程，2019， 29（3）：8-18.

DENG C L. Rediscovery of Plancks formula by principles ofdimensional analysis[J]. Physics and Engineering， 2019，29（3）：8-18. （in Chinese）[2] NEWELL B， CABIATI F， FISCHER J， et al. The CODATA2017 values of h， e， k， and NA for the revision of the SI[J]. Metrologia， 2018， 55（1）： 13-16.

[3] 白光富，袁升，马泽斌，等. 光电效应测普朗克常数新数据处理方法[J].物理与工程， 2013， 23（3）：4-8.

BAI G F， YUAN S， MA Z B， et al. A new data processingmethod of Planck constant measurement through photo electriceffect[J]. Physics and Engineering， 2013， 23（3）： 4-8.（in Chinese）

[4] 徐代升， 王元樟. 基于图形的黑体辐射三大基本定律关系阐述[J].物理与工程， 2012， 22（5）：8-11.

XU D S， WANG Y Z. Describing relationship of three basiclaws of black body radiation based on graph[J]. Physics andEngineering， 2012， 22（5）：8-11. （in Chinese）

[5] DAYWITT C. The Compton radius， the de Broglie radius，the Planck constant， and the Bohr orbits[J]. Progress inPhysics， 2011， 2.

[6] COHEN E R， TAYLOR B N. The 1986 adjustment of thefundamental physical constants[J]. Acta Metrologica Sinica，1987， 59（4）： 1121-1148.

[7] ROBINSON I A， KIBBLE B P. An initial measurement ofPlancks constant using the NPL Mark II watt balance[J].Metrologia， 2007， 44（6）： 427.

[8] LI S， BING H， LI Z， et al. Precisely measuring the Planckconstant by electromechanical balances[J]. Measurement，2012， 45（1）： 1-13.

[9] 王莹， 陈东生. 利用LED的量子特性设计新型普朗克常數测定仪[J]. 大学物理实验， 2012， 25（3）：3.

WANG Y， CHEN D S. Measuring Planck constant usingLED[J]. Physical Experiment of College， 2012， 25（3）：3.（in Chinese）

[10] 林智国， 鲍庆奔， 鲁晓东. 用发光二极管的电致发光过程测普朗克常量[J]. 大学物理实验， 2013， 26（1）：3.

LIN Z G， BAO Q B， LU X D. Measuring Planck constantin electroluminescent process of LED[J]. Physical Experimentof College， 2013， 26（1）： 3. （in Chinese）

[11] 何潜翔，黄建宇，陈乾.功率型LED结温测量方法的实验研究[J].物理与工程， 2020， 30（4）：112-115.

HE Q X， HUANG J Y， CHEN Q . Experimental study onjunction temperature measurement of high-power LED[J].Physics and Engineering， 2020， 30（4）：112-115. （in Chinese）