非线性动力学在磁约束核聚变约束模式转换中的应用

艾媛媛 朱浩

摘 要 非线性动力学在诸如双摆和振荡电路等本科物理教学中扮演着积极的角色。雅可比矩阵作为非线性动力学中的重要概念，常被用来分析不动点的性质。本文中我们先推导了一个二维系统中雅可比矩阵的具体形式，并将其应用到磁约束核聚变约束模式转换模型，最后延伸求解出ZCD模型中各不动点的雅可比矩阵本征值。我们随后调整了模型中的外界加热功率，并使用雅可比矩阵观察模型中非线性动力学性质的变化。经研究发现，外界加热功率的改变会使得ZCD模型极限环的大小发生变化，即功率越大极限环半径越大。极限环半径的扩大导致环与鞍点相交为一个同宿轨，诱使系统产生同宿分岔。

关键词 非线性动力学;雅可比矩阵;约束模式转换模型;同宿分岔

非線性动力学（nonlinear dynamics）是研究系统中各种运动状态的定量和定性规律的科学[1-5]。非线性动力学系统是由一个或一组非线性微分方程描述的随时间变化的系统。若想要预测一个系统的运动轨迹，我们首先需要给出它在微小时间尺度里的性质并列出动力学方程[6]。

人们对非线性问题的认识始于17 世纪。1673年惠更斯发现了非线性现象[7]。在1687年牛顿发现了运动定律和万有引力之后，数学家和物理学家开始尝试将其推广到三体问题，但是并没有取得成功。直到19世纪末，法国科学家庞加莱创立了微分方程的定性理论，为非线性动力学的发展奠定了基础[8]。他首次发现了系统的混沌行为，混沌是一种确定性系统（deterministic system）展示出敏感依赖于初始条件的非周期行为。

1963年洛伦兹在研究大气对流模型时，发现了系统蝴蝶形状的运动轨迹，这标志着混沌理论的诞生[9]。混沌理论广泛应用于各个领域，科学家们也因此发展了很多数学方法，在这个过程中Duffing方程、Van der Pol方程、Mathieu方程等著名的数学模型相继被建立，它们至今仍被人们用来研究非线性系统动力学现象的本质特征[10]。从20世纪60—70年代开始，非线性动力学理论成为一门重要的前沿学科，分岔和混沌的研究随之成为新的研究热点。非线性动力学的思想与方法已被应用到很多的新领域，比如系统生物学、经典力学和社会物理学等。

非线性方程的求解方法相较线性方程更加困难。定性方法和定量方法是研究非线性动力学的两条路径，二者缺一不可。定量方法又分为解析法和数值法。通常情况下，我们很难得到非线性方程的解析解，所以只能求解确定参数时的数值解。定性方法是运用几何的思维方式，从非线性微分方程入手，利用相图（phase plot）来描述微分方程。在相图中，我们可以研究不动点的稳定性，并预测系统随时间演化的行为。在分析具体问题时，定量地去度量稳定性是很有必要的。这需要我们在方程的不动点附近，将非线性方程线性化。在一维向量场中的不动点处，图像的斜率决定了不动点的稳定性。对于多元系统，则需要求解其雅可比矩阵来分析不动点的稳定性。据笔者了解，同时采用定性和定量分析方法研究具体多元系统非线性动力学性质的中文论文并不多。所以本文通过分析磁约束核聚变模式转换中的ZCD模型，来做一个教学式的推导以期回顾教学并延伸到科研。本文框架如下：

（1） 推导二维非线性动力学系统雅可比矩阵的具体形式。

（2） 简单介绍磁约束核聚变装置托卡马克中的L-H 约束模式转换模型。

（3） 通过调整ZCD模型中外界加热功率的参数，以实现核聚变约束模式的转换，并利用相图和雅可比矩阵分析和观察模型中各不动点非线性动力学性质的变化。

2 磁约束核聚变L-H 转换模型

核聚变是两个轻原子核结合组成一个较重原子核的过程，而其中的L-H 约束模式转换则是受控核聚变中一个重要的研究分支[11]。实现核聚变反应需要达到2亿摄氏度的高温，在高温下物质表现为等离子体态，等离子体在高温下剧烈运动，所以这对聚变反应堆的设计有着极高的要求。科学家们因此构建了多种约束等离子体的装置，其中利用磁场来约束等离子体的托卡马克装置是最为有效的。托卡马克装置的反应原理为氢元素的同位素氘（21H 或D）与氚（3 1H 或T）聚合反应生成氦（4 2He）。实现核聚变反应需要满足劳森判据（Lawson Criterion）nTeτE >1021m-3sKeV，其中n 为等离子体密度，Te 为等离子体温度，τE 为能量约束时间。虽然根据爱因斯坦质能方程计算，很少的反应物便可以释放大量的能量，但是目前在实验上等离子体的约束时间是非常短的，所以人工受控核聚变的实现需要更高的约束水平和更长的约束时间。

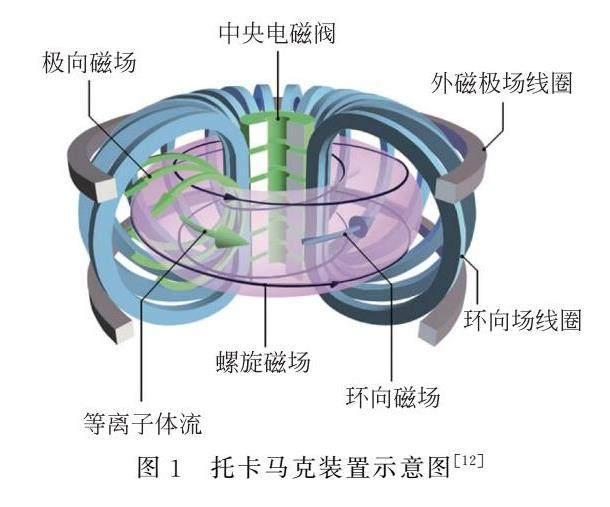
托卡马克装置是由两个主要磁场合成一个螺旋磁场，使等离子体绕磁力线做拉莫尔回旋运动。其中，一个磁场是由缠绕在圆环形真空室外面的铜线圈产生的环向磁场，另一个是由等离子体中的带电粒子电流产生的极向磁场，如图1所示。在非均匀磁场下等离子体会发生漂移[13]，等离子体之间的相互作用会产生能量输运过程。由等离子体湍流引起的输运过程称为反常输运。等离子体边缘湍流较强使得温度梯度较弱，会损失大量能量，这导致托卡马克处在一个较低的约束水平，即低约束模式（L 模式）。在1982年，ASDEX 托卡马克装置加热期间能量约束问题得到了大幅改善。Wagner等人发现在L模的基础上通过提高加热功率，并达到一定的阈值之后会实现L-H 模式转换，H 模式为高约束模式[14]。H 模式的边缘区域由于密度和温度突然增长而出现边缘输运垒，整体约束水平得到极大的提升。因此H 模式是未来反应堆的理想约束模式。

3 外界加热功率引起的同宿分岔

本节我们通过改变外界加热功率q，用非线性动力学的方法对ZCD 模型中极限环的性质做进一步研究。图2～图6为q 值不同时温度梯度N 、等离子体湍流强度E、带状流U1、测地声模U2以及加热功率q 随时间变化的图像（左侧）和系统在相空间（E， U2， N ）中的时间演化（右侧），其中箭头表征演化的方向。

图2中q 值为0.47，其图像包括了四个阶段，分别为H 模式、L模式、T模式和O模式。四个模式分别对应到相空间中我们所求解的四个不动点A 、B、C、D ，在图1（b）中已标出。我们在图1（a）中观察到，在t=6500附近带状流U1 逐渐消失，U2 随之增长，湍流E 被抑制，从而出现了一个非常稳定的极限环。在极限环状态下U1 为零，E、N 、U2 不为零。表1中显示不动点D （极限环）处本征值包含一对共轭复数，且实部为正数，轨迹螺旋运动至极限环。实际的实验中系统会通过极限环振荡模式达到H 模，H 模式为N 更高的状态。为研究控制因子q 对系统约束水平的影响，我们在图3～图6中改变了外界加热功率q，其值分别为q=0.49、q=0.52、q=0.54 和q=0.549。

我們发现在图2至图5显示的变量随时间变化的图像（a）中，随着q 值的增大，轨迹在第一个不动点A（H 模）的持续时间明显增长，q 由0.47增至0.54时，t 由约400增至约2500。但是轨迹在B 点（L模）和C 点（T 模）处的持续时间几乎不变，即H 模对于q 值的大小更为敏感。q 值的增大直接导致N 值增大，这导致带状流U2 被抑制，在（E，N ）平面中U2 的最大振幅减小，且振荡频率增加。除此之外，最明显的变化是极限环的周期和半径，它们更加依赖于外界加热功率q 值的大小。具体表现为q 值越大，极限环的周期越长，半径越大。极限环周期的延长使得系统处在H 模的时间更长，即约束时间更长;极限环半径的增大导致轨迹向（E，N ）平面和（U2，N ）平面靠近。极限环周期的变化具体体现为，U2 的振幅变化范围越来越大，最小值越来越趋近于0，湍流便不能被很好的抑制，在每个周期中湍流存在急速增长和急速下降的情况。在图5中，伴随着U2 和E 之间的相互作用，极限环与鞍点A 和鞍点B 相重合，系统发生了同宿分岔。

通过数值计算，我们在表1中看到当q=0.54时，雅可比矩阵的本征值反映不动点D 是一个鞍点，而并非图5（b）中的极限环。在同宿分岔中，随着系统中参数变化，极限环与鞍点可以彼此越来越近直至相交。环与鞍点在相交后成为一个同宿轨道。在图2（b）至图5（b）相图中我们可以看到在q 值在达到0.54之前，极限环由于周期延长越来越接近A 、B 这两个鞍点。当q 值增加至0.54时，极限环膨胀且爆裂为鞍点，同时产生一条同宿轨（见图5），q=0.54即为系统产生同宿分岔的一个阈值。由于鞍点不稳定的性质，当q 大于0.54时，鞍形连接会分裂，导致系统无法回到同宿轨道，即环被摧毁。同宿分岔是全局分岔的一种类型，其会导致相空间中轨迹的拓扑结构发生变化，而且这种变化不像局部分岔那样局限在一个小的邻域内，拓扑结构的变化可以延伸到任意大的距离。如图6（b）所示，整个系统形成了一条同宿轨道。在图6中，同宿分岔导致U1 周期振荡，湍流被更好地抑制，约束水平达到最高。

4 结语

在本科物理教学中会遇到一系列非线性微分方程的求解和分析问题，本文回顾并利用了非线性动力学中的雅可比矩阵来分析磁约束核聚变的约束模式转换模型。雅可比矩阵的本征值反应了不动点附近变量的衰减率，四维方向上的衰减率共同决定了不动点的性质，这为我们预测模型随时间的演化提供了数值依据。在ZCD 模型中，我们发现外界加热功率q 值会影响到极限环的周期，q 值越大极限环的周期越长。极限环半径的增大导致了极限环与鞍点相重合，诱使系统产生同宿分岔，出现一条同宿轨。在产生同宿分岔时，极限环状态的不动点D 与鞍点A 非常接近，导致本征值的计算结果与所绘制相图中不动点的性质不相符，雅可比矩阵可以部分解释磁约束核聚变中L-H 转换模式。在物理教学中应该注意到求解雅可比矩阵的本征值不能准确地描述轨迹的性质，需要结合相图具体分析。

参 考 文 献

[1] 刘锦，张孟.弹簧车摆的动力学模拟研究[J].物理与工程，2021，（5）：93-97.

LIU J， ZHANG M. Simulation study on the dynamics ofspring car pendulum[J]. Physics and Engineering， 2021，31（5）： 93-97. （in Chinese）

[2] 李万祥，何玮，唐恭佩.一类复摆系统的非线性动力学研究[J].华中科技大学学报：自然科学版，2007，（5）：27-30.

LI W X， HE W， TANG G P. Research on nonlinear dynamicsof a double pendulum system[J]. Journal of HuazhongUniversity of Science and Technology （Nature scied）， 2007， 35（5）： 27-30. （in Chinese）

[3] 张连芳，傅敏学，刘滢滢，等.混沌实验教学之路[J].物理与工程，2013，（1）：21-24.

ZHANG L F， FU M X， LIU Y Y， et al. The way of educationfor chaos experiment[J]. Physics and Engineering，2013， 23（1）： 21-24.（in Chinese）

[4] 李明达，董乔南，杨亚利，等.利用非线性动力学系统研究混沌现象[J].物理与工程，2019，（6）：77-84.

LI M， DONG Q N， YANG Y L， et al. Study of chaos withnonlinear dynamical system[J]. Physics and Engineering，2019， 29（6）： 77-84.（in Chinese）

[5] ZHU H， CHAPMAN S C， DENDY R O. Robustness of predator-prey models for confinement regime transitions in fusionplasmas[J]. Physics of Plasmas， 2013， 20（4）： 042302.

[6] STROGATZ S H. 非線性动力学与混沌[M]. 孙梅， 汪小帆等， 译. 北京： 机械工业出版社： 2016.

[7] 周道其. 科学家揭开惠更斯复摆钟之谜[J]. 现代物理知识，2002， 14（5）：1.

ZHOU D Q. Scientist shave solved the mystery ofHuygenscompound pendulum clock[J]. Review of World Invention，2002，14（5）： 1. （in Chinese）

[8] 陈明晖，邓明立.庞加莱微分方程定性理论研究初探———兼纪念庞加莱诞辰150周年[J].科学.2004，（1）：29-31.

CHEN M H， DENG M L. A Preliminary study on theQualitative Theory of Poincarés differential Equation—Alsocommemorating the 150th anniversary of Poincarés birth[J]. Science， 2004， 56（1）： 29-31. （in Chinese）

[9] LORENZ E N. Deterministic nonperiodic flow[J]. Journalof the Atmospheric Sciences， 1963，20（2）：130-141.

[10] 叶美盈.一种非线性动力学系统数值模拟的新方法[J].云南师范大学学报：自然科学版，2000，（2）：33-36.

YE M Y. A new approach to the numerical simulation ofnonlinear dynamics[J]. Journal of Yunan Normal University（Natural sci ed）， 2000， 20（2）： 33-36. （in Chinese）

[11] MCCRACKEN G H， STOTT P.宇宙能源———聚变[M]. 核工业西南物理研究院翻译组. 北京：原子能出版社，2008.

[12] LI S， JIANG H， REN Z， et al. Optimal tracking for a divergent-type parabolic PDE system in current profile control[C]//ZHANG X G. Abstract and Applied Analysis.New York： Hindawi Publishing Corporation， 2014： 1-8.

[13] 刘爱红，佘守宪.轴对称缓变磁场中的等离子体与磁约束原理[J].物理与工程，2002，（5）：14-17.

LIU A H， YU SH X. Plasma in slow-varying magneticfield with axial-symmetry and principle of magnetic confinement[J]. Physics and Engineering， 2002， 12（5）： 14-17. （in Chinese）

[14] WAGNER F. Regime of Improved Confinement and HighBeta in Neutral-Beam-Heated Divertor Discharges of theASDEX Tokamak[J]. Physical Review Letters， 1982， 49（19）：1408-1412.

[15] BURRELL K H. Effects of E × B velocity shear and magneticshear on turbulence and transport in magnetic confinementdevices[J]. Physics of Plasmas， 1997， 4（5）：1499-1518.

[16] MALKOV M A， DIAMOND P H. Weak hysteresis in asimplified model of the LH transition[J]. Physics of Plasmas，2009， 16（1）： 012504.