进动现象的直观解释

熊志松 程运华

摘 要 进动是刚体力学中的一项重要内容，但由于涉及复杂的定点转动问题，其数学推导过程比较繁琐，大部分教材的相关内容晦涩难懂，再加上进动现象本身的反直觉的特点，使得很多人对进动现象的规律并未真正理解。本文首先从质点的惯性入手，通过与简单的质点力学问题类比，直观地解释进动。接着，我们深入探讨回转力矩的本质，只借助简单的受力分析和计算，就推得了进动的结果，我们的方法避免了复杂的刚体力学理论计算，为理解进动提供了一种新思路。

关键词 刚体;陀螺;进动;回转力矩

旋转的刚体在受到垂直于转轴的力矩作用时，会在原有的自转上叠加一个新的转动，这就是进动现象。以一个玩具陀螺为例，一旦它绕自身轴转动后发生倾斜时，其自转轴就会绕竖直轴转动。如图1所示，陀螺绕自身转动，若自转方向为图中标出的方向（ω 旁的箭头所示），则进动角速度竖直向上。若陀螺反向自转，进动角速度也将反向。

对大多数人来说，进动现象具有反直觉的特点。陀螺明明已经倾斜了，但却并不倒下，好似有一种与重力抗衡的力往上支撑着陀螺，但这个与重力抗衡的力到底是如何产生的，看起来不那么容易找到。

在常见的大学物理和力学课本中，一般只根据角动量定理给出一个简单的解释。其基本思路是，相对于地面接触点O，重力的力矩M 沿水平方向，与刚体的自转角动量L 垂直，根据角动量定理dL=Mdt，dL 必然也沿水平方向，并时刻保持与L 垂直的关系。这样一来，刚体的角动量L 自然就绕着通过点O 的竖直轴转动起来了。若陀螺的自转轴与竖直方向的夹角为θ，设在dt 的时间内，自转轴绕竖直轴转过的角度为dφ，则角动量L的增量的大小为dL =Lsinθdφ，而dL =Mdt，联立此二式得进动角速度Ω 为

因此，刚体进动角速度与外力矩成正比，与自转角动量成反比。

显然，上面这种解释只是给出了进动满足的规律，但陀螺为什么没有倒下？ 陀螺为什么会发生进动？ 并且，既然刚体未受到竖直方向的力矩作用，为什么却获得了竖直方向的角动量呢？ 若依据理论力学的详细计算和分析，当然能解答这些问题。但由于数学计算过程相对较为复杂[1-2]，对大多数非物理专业的学生来说难度太大。为避免复杂的计算过程，一些教材仅给出定性解释。

例如，在梁昆淼编著的《力学》的“旋转的重刚体的定点运动”部分[3]，作者用回转力矩解释陀螺为什么不倒的问题，其核心点是，重力作用下的傾斜和进动各自导致一个回转力矩，前者令自转角速度转向重力矩方向，形成进动;后者抵抗重力力矩，避免了刚体倾倒。

对刚体为何转而不倒的问题，另一种常见的解释是，在随刚体进动的参考系中，刚体上的点受科里奥利力作用，从而导致一个与重力矩抗衡的力矩作用[4]。而对于刚体为什么不受进动角速度方向的力矩作用却产生进动的问题，现有的文献很少涉及。梁昆淼给出一种解释是[5]，当水平面内转动的刚体向下倾斜时，其角动量会形成一个竖直向下的分量，但由于在竖直方向系统并未受力矩作用，竖直方向的角动量应守恒，为了保证这一点，系统也会同步产生一个竖直向上角动量分量，这样就形成进动了。

本文将通过类比思想和受力分析直观地解释进动。一方面，我们从惯性的角度来理解进动。我们先通过曲线运动了解垂直于速度的力作用下的物体的运动特征，接着分析地球上空飞行器受推力作用后轨道的变化规律，基于此构造一个思想实验以解释进动。另一方面，我们通过对静止和自转的陀螺的受力分析，从力和加速度的角度理解回转力矩的本质，并通过计算陀螺上点的速度和位移直观地解释刚体产生进动的原因。

1 基于惯性的直观理解

静止的物体受到外力作用时，它将沿着力的方向运动。但若受力作用的物体有初速度，其运动方向不再只由力来决定。例如，一个沿直线运动的物体，若受到一个垂直于速度的力，它将作曲线运动，典型的例子如平抛运动。

由于质点具有水平方向初速度，在重力的加速下，质点获得了竖直速度，质点沿抛物线运动，速度沿抛物线的切线方向（见图2（c））。质点既不会被直接推到下方的一条水平线上运动（见图2（a）），也不会直接沿竖直向下的方向运动（见图2（b））。显然，这是由力与惯性共同导致的。假若质点真的沿着y 轴运动，那它的水平速度就不起作用了，相当于质点的惯性消失了！

因为有惯性，当质点的初速度与外力不在一条直线上，质点既不能沿着原来的速度方向运动，也不能沿着力的方向运动，只能沿着一条曲线运动。其实，无论力是否与速度垂直，惯性作为物体反抗外力的固有本性总是存在的，只不过看起来， 惯性对垂直力的反抗更加明显———它会使速度转向，质点的轨迹既不会直接沿着力的方向完全转过去，也不会沿着力的方向发生平移，而是成为一条曲线。典型的案例是洛伦兹力，由于它始终与速度垂直，它只能改变速度的方向，使带电粒子作匀速圆周运动。虽然粒子受到指向圆心的力，但却不会落入圆心，而是拐弯过去了，这是惯性抵抗外力作用所导致的必然结果。

类似地，刚体转动时，如果没有外力作用迫使它的转动改变，它将会一直转下去。这种惯性用转动惯量描述，它与质点的质量相对应。对没有转动的刚体来说，它完全听从外力矩的安排，例如静止的陀螺倾斜后会直接倒下。而当刚体在转动的情况下受垂直力矩作用时，它的转动方向就不沿着外力矩的方向了。陀螺进动就是这样产生的，这样的例子还有很多，例如，落在地上的圆盘之所以会旋转一会儿才会停息，也是因为重力矩与自转角动量方向不一致导致的。

但从刚体角度来解释进动并非易事，既然刚体是由质点组成的，质点的集体必然体现刚体行为，我们尝试从质点出发来解释进动。

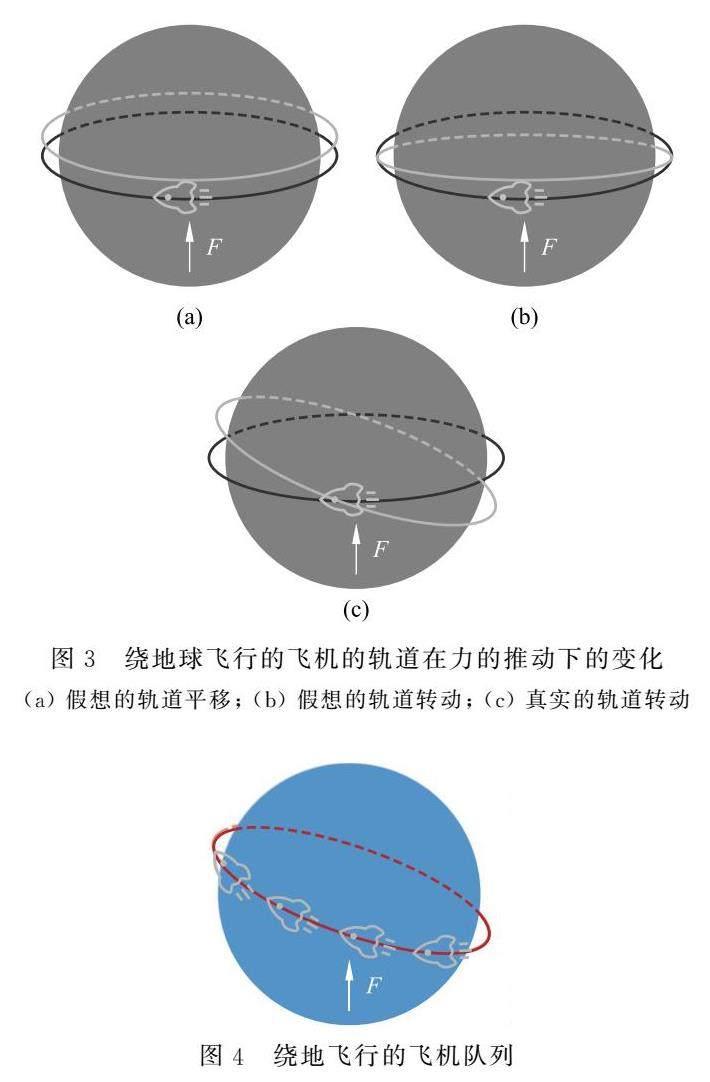
设有一架飞机沿赤道方向（如图3中深色线）绕地飞行。若每当飞机经过某点时，给它一个正北向的推力，根据质点惯性对外力的反抗作用，飞机的轨道不会直接向上平移（图3（a）中浅色线），也不会像图3（b）所示那样发生翻转，而会变为像图3（c）所示的那样斜的轨道。

实际上，一种调整卫星轨道的方法正是基于这一原理。在发射卫星时，可在靠近赤道的地方沿赤道自西向东方向发射，因为这样能充分利用赤道处地面高达465m/s的移动速度。待到卫星升空之后，可在空中再作调整，以使卫星进入预定轨道。

下面来做一个思想实验。假设有大量的飞机列队沿一条共同轨道绕地飞行，若对所有飞过一个确定点（例如图3中正前方标F 处）的飞机都施加一个向北的推力，那么这些飞机的共同轨道就会像上面那样发生倾斜，如图4所示。现假想这些飞机是在一个中空的管状巨环内列队飞行，巨环套在地球上，环自身质量不计，则飞机沿环内飞行就相当于巨环在绕地球旋转。若在环的某处施加一个向北的推力，并在地球背面正对处施加一个向南的推力，那么这个由飞机组成的巨环也会发生同样的倾斜。更一般的，若考虑一个充满流动液体的管子，或者更直接地，考虑一个旋转的金属环，当它受到同样的推力时也会发生类似的倾斜，如图5所示。

由此可见，当你试图转动一个正在旋转的物体的转轴时，它仿佛总是不太听话。上面这个环就是这样，它并没有沿着这个推力的方向转动———推力的力矩的方向水平向左，而是绕另一个垂直的方向转起来了！ 看起来的效果是，你推的那个力的作用点，好像神不知鬼不觉的往前移动了四分之一圆周，然后在那个位置起作用。

注意，上面说作用点“往前移动”时之所以用“好像”二字，因为这只是一种帮助理解的说法，实际力作用点并未移动。根据刚体力学中滑移矢量的概念，要保持作用效果不变，力的作用点不能随便移到其他点，只能沿着力的作用线方向滑移。对转动的环上的一对推力来说，若移动它们的作用点到另一条直径的两端，环的运动情况必将不同。所以，转动的环受力也是滑移矢量，其作用点并非真的移动了。

这种转动的物体由于受到垂直于转轴的力矩作用而形成的运动就是进动。它看起来反直觉，但其实是很自然的，因为任何自转的物体总可看作无数个绕轴自转的环聚合而成，每个环又可被看作由无数个沿着环运动的点（无限小的飞机）组成的，根据上面的思想实验，每个点在推力的作用下的轨道倾斜是显而易见的，这将导致物体的整体发生进动。

综上所述，质点的惯性构成刚体的惯性，与质量反抗力的作用类似，转动惯量也反抗外力矩的作用，当刚体所受力矩与自转角动量方向垂直时，刚体不会绕力矩的方向发生转动，而是绕另一个与之垂直的方向发生转动，即形成进动。

2 从力与加速度来解释

为什么刚体不绕外力矩的方向转动，而是绕与外力矩垂直的方向转动呢？ 从上面环的例子中，我们看到，真正导致环转动的力相当于作用在沿环移动四分之一圆周后对应的位置。换句话说，力虽然在某个位置施加了作用，但其作用点却好像瞬间沿环的自转方向移动了四分之一的圆周！ 在那个新的位置产生的力矩正好相对于外力力矩转过90°的角，也就是与外力矩垂直的方向，这个力矩被称作回转力矩。

显然，只有当环在自转时，才会导致回转力矩。那么，为什么转动的刚体就会产生这种神奇的作用转移，从而导致回转力矩呢？ 下面我们从受力分析的角度来仔细探讨这背后的玄机。

为简单起见，设陀螺由轻杆和质量均匀的轮子构成，且作为自转轴的轻杆是水平的。先考虑陀螺没有自转的情形，轮子受重力矩作用，如图6所示，下面换一个角度来看这个重力矩。

我们知道，力偶作用导致力矩，例如回转力矩就是基于科里奥利力系的力偶形成的。因此，任何力矩总可看作力偶，也等效为力或力系作用。故陀螺所受重力矩导致在盘上各点受到不同的力！ 对于轮子的上半部分，会受到一个向右的力，而对轮子的下半部分，则会受到一个向左的力。但你可能觉得奇怪：重力向下，怎么会导致向左和向右的力呢？ 因为陀螺上各点并不是孤立的，除了重力，它们还受到约束力，从而使陀螺轮上的点的受力有不同的轴向分量，下面给出详细分析。

如图7所示，当陀螺处于水平的瞬间，轮上各点速度为零，所以也就没有法向加速度;但由于重力矩作用，根据刚体的转动定理，陀螺具有角加速度。设该角加速度为β，则各点的切向加速度为aτ=βr，其中r 是对应点绕O 轴的转动半径。据此，轮子上的点受到的切向外力为maτ=mβr。设轮子的半径为R，以轮子最高点对应的轮半径作為起始位置，轮子边缘上相对起始位置转过θ 角的点受到的切向力的轴向分量为maτRcosθ/r，即mβRcosθ。

由此可见，轮上个点的轴向位移与轴向力的方向相反。这看起来有点违反直觉，但实际情况的确如此。

为了说明这一点，我们来仔细分析轮子边缘最上方的点的情况。图11是进动陀螺（见图9）的俯视图。在某个时刻t，轮子顶点（图中灰点）速度方向水平向左，如图中间部分所示;而在之前的某个时刻t-Δt，这个点处在轮的右端，那时轮子正从左侧绕进动轴转过来，如图左侧部分所示;在之后的t+Δt 时刻，该点已运动到轮的左端，而那时轮子已经摆到右侧，如图右侧部分所示。若把该点在三个时刻的位置用光滑的曲线连起来，将得到一条往上凸起的曲线。由此可见，当点位于顶点时，它离转轴O 最近，也就是说，它的位移是指向O 的，而此处的轴向力是背离O 的。可见，力与位移的方向的确相反。

实际上，考虑到这些点一方面在随轮子自转，现在又在进动，综合来看，这些点在作曲线运动，那么曲线运动必然受到向心力的作用，而向心力总是指向曲线的曲率中心的，既然最高点处的轴向力指向远离O 的方向，它作为向心力所决定的曲线运动的曲率中心当然也在远离O 的那一侧了。

3 结语

本文通过将刚体的运动与质点运动的类比，将进动理解为刚体惯性的所导致的结果，在此基础上，我们构建了一个思想实验来理解进动现象。当转动的刚体受垂直于角动量的外力矩作用时，其作用效果相当于一个未自转的刚体在垂直的方向受到一个力偶作用，这导致了回转力矩。进一步地，我们基于力和运动的简单计算，深入理解回转力矩的本质，通过分析陀螺上各点的速度和位移的分布情况，直观地解释了陀螺进动的物理机制。

参 考 文 献

[1] 江先国.对称陀螺运动的简明分析方法[J].大学物理，1988（10）：5-8.

JIANG X G. A concise analysis method of symmetric gyromotion[J]. College Physics，1988（10）： 5-8. （in Chinese）

[2] 梁昆淼.令人困惑的定点转动[J].大学物理，2010，29（9）：55-58.

LIANG K M. Confusing fixed-point rotation[J]. CollegePhysics， 2010， 29（9）： 55-58. （in Chinese）

[3] 梁昆淼.力学上册[M].4版.北京：高等教育出版社，2010.

[4] 刘斌.力学[M].合肥：中国科学技术大学出版社，2013.

[5] 梁昆淼.旋转的陀螺为什么不倒[J].物理教学，1980（3）：12-13.

LIANG K M. Why does the spinning top not fall down[J].Physics Teaching， 1980（3）： 12-13. （in Chinese）