电磁/液压制退机对火炮运动特性的对比分析

张伽博，李强，张超，孙志群

(1.中北大学 机电工程学院，山西 太原 030051；2.中国船舶集团有限公司第七一三研究所，河南 郑州 450015)

电磁制退机是一种采用电磁阻尼缓冲技术的火炮反后坐装置,与传统的液压制退机相比较,具有工作噪声低、无液体介质、结构简单等天然优势,避免了传统反后坐装置密封失效、介质空化、零件寿命短等弊端,因此具有更高的可靠性与更低的维护难度,是一种新型的高效反后坐装置。

电磁阻尼缓冲技术最早应用于低速、低载的汽车缓震、轨道制动领域,其基本制动原理与特性已得到国内外学者的广泛研究,并逐渐被应用于火炮反后坐领域。李子轩等[1-2]提出了一种永磁式电磁制退机,并考虑强冲击载荷下的去磁现象,建立了基于改进指数的去磁模型与矢量磁滞模型,通过冲击试验与有限元仿真等方式对电磁制退机的制动特性进行了研究与优化;黄通等[3]提出了一种新型电磁制退机结构方案,对电磁制退机的制动特性进行了研究,并通过调控负载阻值实现了后坐阻力与后坐运动特性的控制;沈艳萍等[4]针对永磁式制退机建立多目标后坐阻力优化模型并通过现代优化计算方法减弱了去磁效应影响下后坐阻力曲线马鞍特征;谢子豪等[5]针对永磁式制退机在不同布置方式下对炮口振动的影响进行对比性研究,通过数值模拟方法得到了炮口水平角、高低角位移与高低齿弧、衬瓦的接触力。

综上可知,国内学者对电磁制退机的制动特性已经进行了深入的研究。为了解电磁制退机对火炮运动特性的影响,笔者针对某口径火炮设计一种圆筒型永磁式制退机,替代原节制杆制退机,建立单火炮发射动力学模型,利用动力学软件搭建刚柔耦合仿真模型,通过分析部分动态响应结果,对采用永磁式电磁制退机与节制杆式液压制退机的火炮运动特性进行对比分析。

1 电磁制退机工作原理

圆筒型永磁式制退机主要由初级与次级构成,如图1所示,永磁式制退机初级包含永磁体、磁靴及连接件,次级包含导体筒与导磁筒,图中N、S表示永磁体轴向充磁方向相反。当火炮后坐运动开始时,初级与次级发生相对运动,在导体筒内部出现感生涡流,涡流的感应磁场与永磁体磁场互相作用产生电磁阻尼力[6],即电磁制退机力。

2 反后坐装置分析设计

2.1 反后坐装置参数

针对某口径火炮的后坐运动特性要求,在相同的射击载荷与后坐质量下,为保证永磁式制退机与节制杆制退机工况下火炮的运动位移、时间一致,圆筒型永磁式制退机主要结构参数如表1所示。

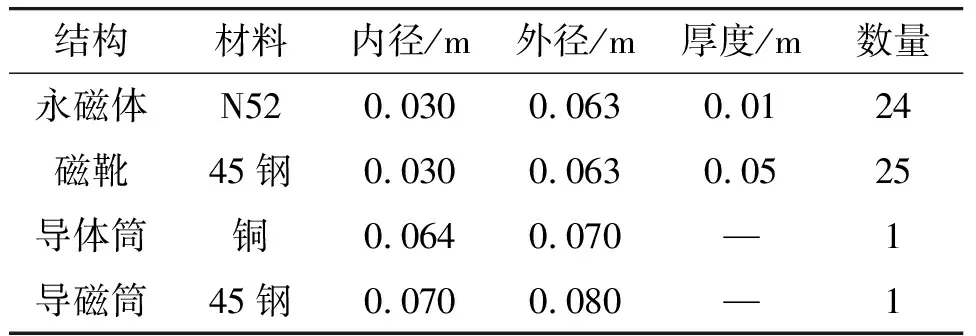
表1 圆筒型永磁式制退机结构参数

在上述结构参数下,考虑导体筒的集肤效应[7-8],永磁式制退机的制退力计算模型为

(1)

式中:N为永磁体数量;σ为导体筒材料的导电率;v为初级与次级的相对运动速度;τ为磁极厚度;τm为永磁体厚度;Br为导体筒空气间隙处的磁感应强度;r0导体筒外径;ri为导体筒内径;δ为导体筒表面的穿透深度。

节制杆制退机主要结构参数如表2所示。

表2 节制杆制退机结构参数

在上述结构参数下,节制杆制退机力的计算模型为[9]

(2)

火炮反后坐装置采用弹簧式复进机,其初力F0为2 kN,弹簧等效刚度K为20 kN/m,复进机力计算模型为

Ff=F0+K·x,

(3)

式中,x为后坐部分位移。

火炮射击时,后坐部分后坐、复进运动的动力学方程为

(4)

式中:火炮后坐部分质量mh=130 kg;Fpt为炮膛合力;FR为运动阻力,包含制退机力Fh、复进机力Ff、摩擦力Fmc与重力沿运动方向分力Fz,即

FR=Fh+Ff+Fmc±Fz.

(5)

2.2 反后坐装置运动分析

火炮射击时的炮膛合力曲线如图2所示。

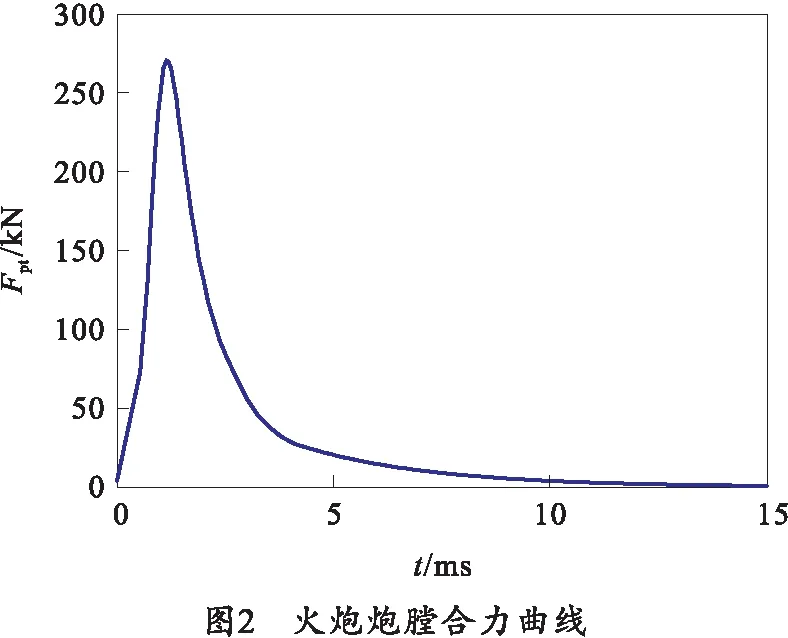
依据式(1)～(5),以后坐方向为速度正方向,分别对永磁式制退机与节制杆制退机下的火炮后坐附近运动进行计算,得到火炮在0°射角下的位移、速度变化规律,如图3、4所示。

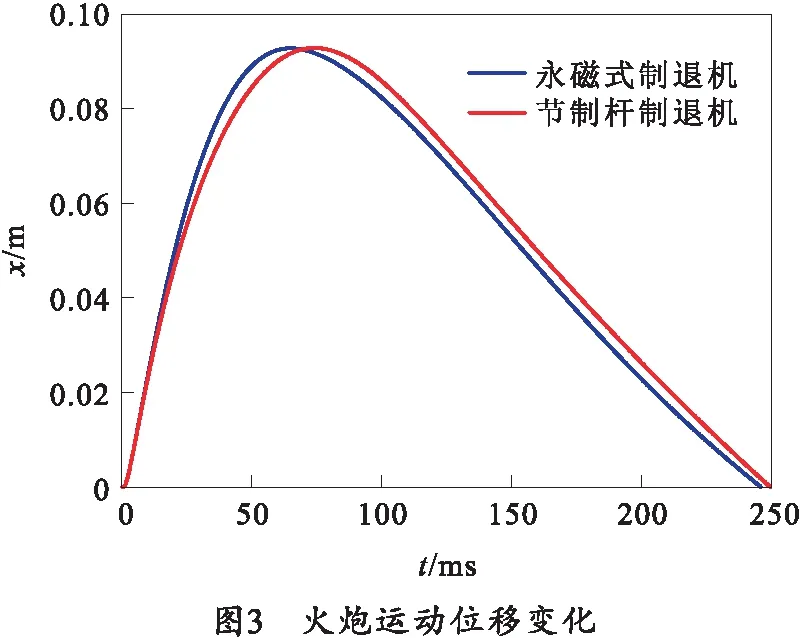
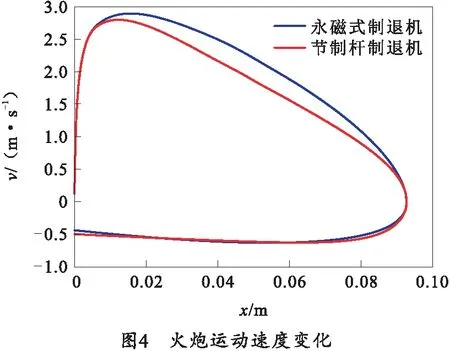
由图3、4可知,采用永磁式制退机与节制杆制退机火炮运动位移与速度变化差别较小。在后坐加速阶段,采用永磁式制退机,后坐速度峰值更高。在后坐减速阶段,采用永磁式制退机速度曲线的充满度比采用节制杆制退机更好,始终维持更大的后坐速度,因此所用后坐时间更短。在复进阶段,采用永磁式制退机在复进加速阶段整体速度小于采用节制杆制退机,两种制退机下火炮复进至0.06 m处均达到复进速度峰值,火炮运动诸元如表3所示。

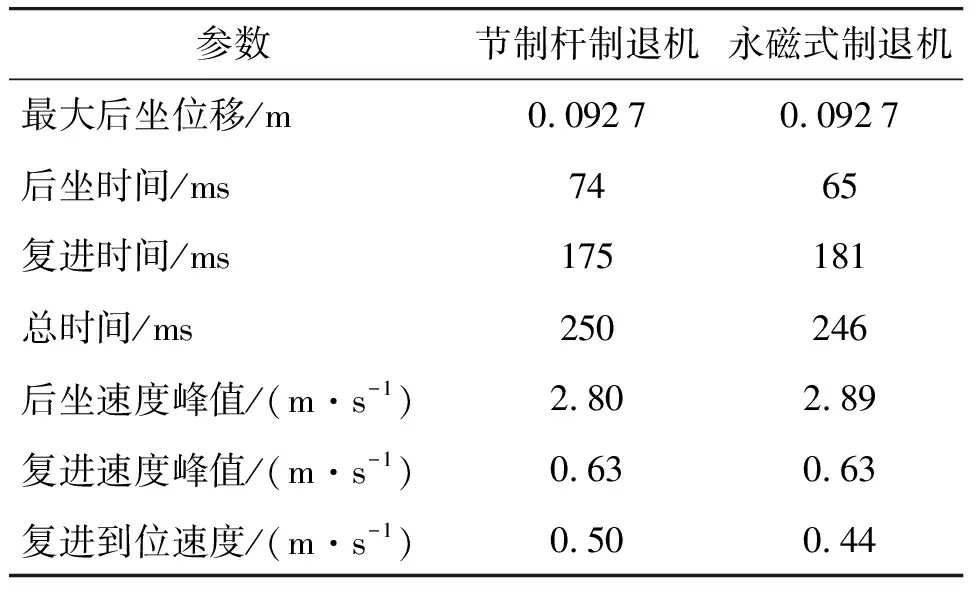
表3 0°射角下火炮运动诸元

由式(1)、(2)可知,当结构参数确定时,永磁式制退机的制退力受运动速度v与导体筒空气间隙处磁感应强度Br的共同影响,因此在火炮炮膛合力的强冲击载荷作用下,相比于节制杆制退机,永磁式制退机具有更好的阻尼力平台效应,如图5所示。

由图5可知,在后坐阶段,永磁式制退机力在达到峰值后缓慢降低,在90%的后坐行程内制退机力始终保持在3.5 kN以上,节制杆制退机力在达到峰值后迅速降低;在复进阶段,永磁式制退机力在复进加速阶段增长更加剧烈,剩余行程内力值变化更加平缓,各阶段制退机力峰值如表4所示。

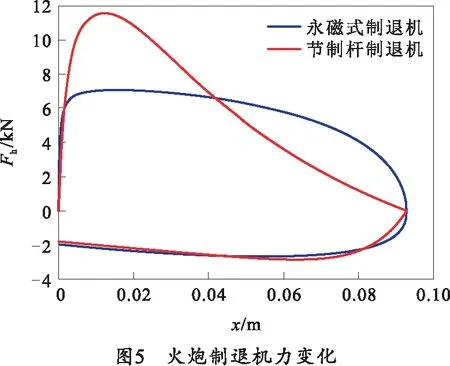
表4 0°射角下制退机力变化情况

由以上分析可知,在整个运动行程内,永磁式制退机力的峰值低且变化平缓,因此能在最大行程范围内保持较高的制退能力,节制杆制退机力峰值高,对制退机构件的强度设计有更高要求。

3 动力学仿真分析

由式(5)可知,火炮运动阻力的变化趋势主要受复进机力与制退机力影响,而复进机力为位移的线性函数,因此平台效应更为显著的制退机力可以使运动阻力在火炮运动行程内趋于平缓,从而改善炮身与炮架之间的相互作用,提升火炮的后坐稳定性。为验证这一特性,对某口径火炮进行刚柔耦合模型的搭建,利用有限元及动力学分析软件对两种工况下的火炮运动进行仿真。

3.1 柔性体模型

利用有限元分析软件ABAQUS对火炮运动部分进行基于lanczos法的模态分析[10],并设置MPC耦合结点生成子结构,最终得到模型的中性文件。各柔性部件材料及单元类型如表5所示,火炮柔性部件的前10阶约束模态如表6所示。

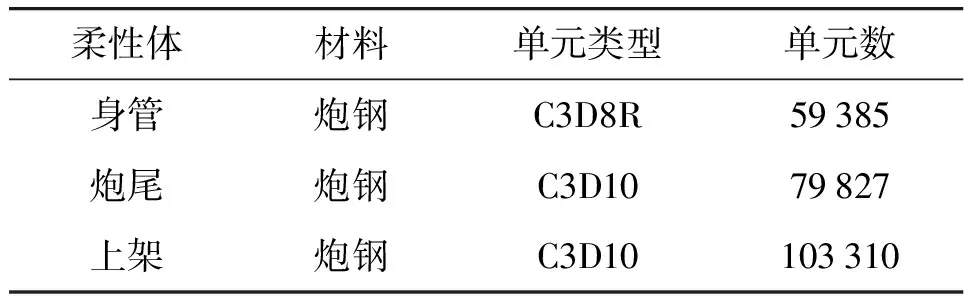
表5 柔性体有限元参数

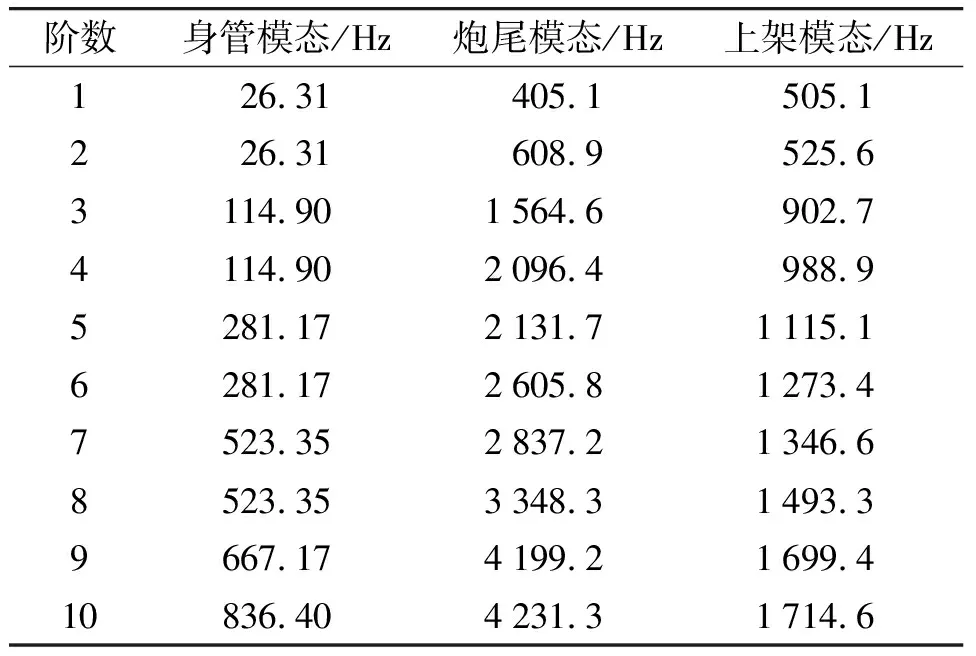
表6 火炮柔性部件约束模态

3.2 动力学模型

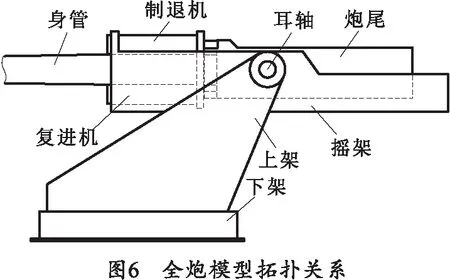
利用中性文件生成身管与后坐部分柔性体,搭建刚柔耦合模型,全炮模型拓扑关系如图6所示。在膛底施加炮膛合力,在反后坐装置对应位置施加如式(1)～(3)所示的制退机力、复进机力以及摩擦力,并考虑身管的初始挠度,分别对0°、15°和45°射角工况进行求解。

对于建立的刚柔耦合模型,ADAMS软件在集成约束方程后可以自动建立系统的微分代数方程,并将二阶微分方程降阶为一阶微分方程直接求解,该方程为Index3微分方程[11]:

(6)

式中:P为系统的广义动量;H为外力的坐标转换矩阵。

4 运动特性对比

4.1 炮口位移情况

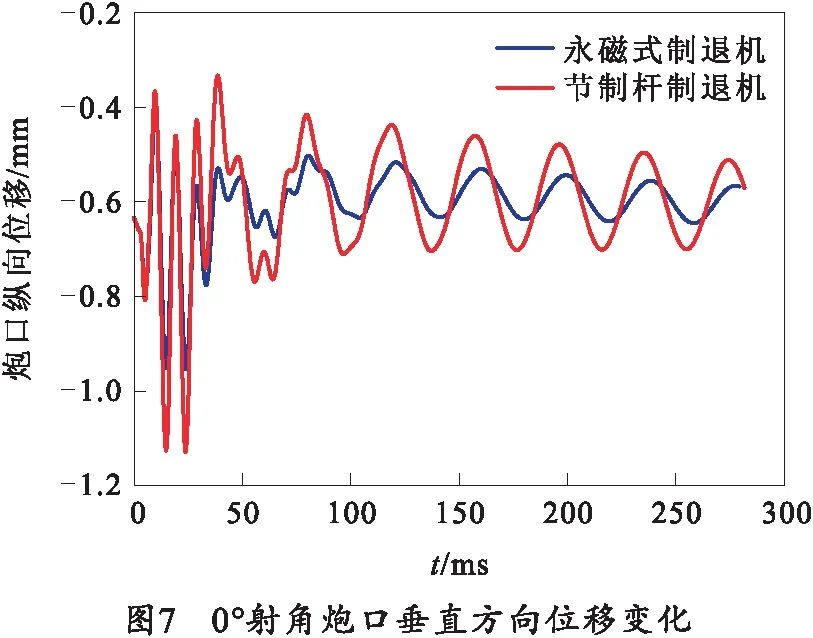
当身管在重力作用下振动幅值衰减至10%时,身管的初始挠度为0.66 mm,以此时刻为时间零点,0°射角下炮口垂直方向位移变化如图7所示。由图7可知,在0°射角下,火炮采用永磁式制退机与采用节制杆制退机相比,炮口垂直方向振动频率相近,幅值差异较大。在后坐阶段,二者变化比较剧烈,在复进阶段幅值变化趋于平缓。

对0°、15°和45°射角工况下炮口振动幅值变化特征进行提取,得到如图8～10所示的振动幅值变化。

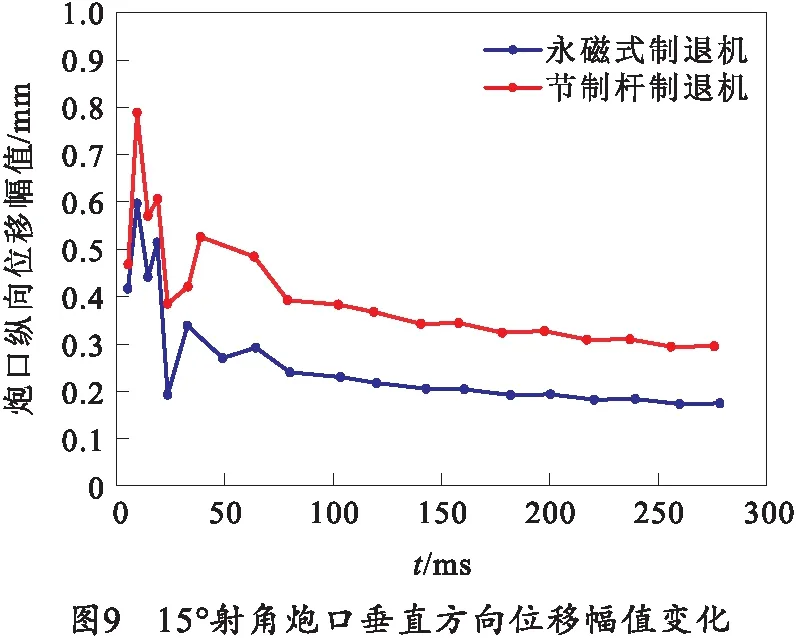
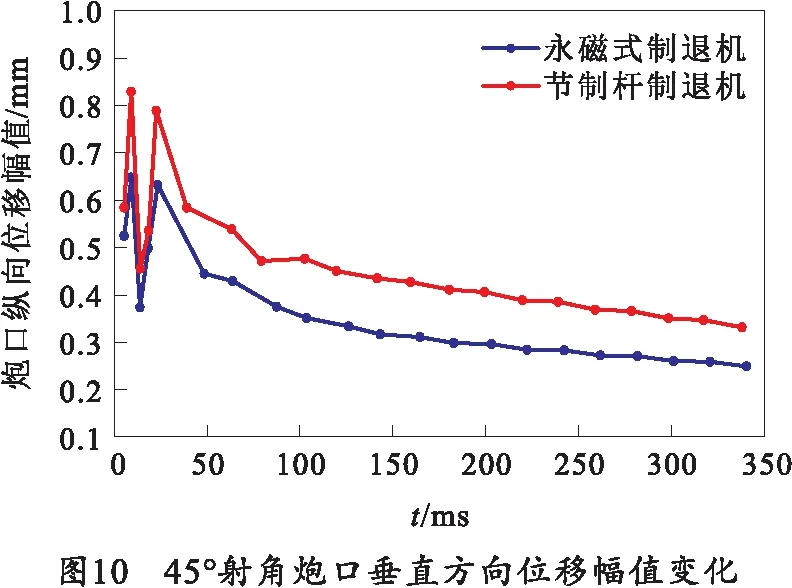
由图8～10可知,相同射角下,采用永磁式制退机时炮口振动幅值更小,在0°、15°与45°的不同射角下,与采用节制杆制退机相比,炮口平均振动幅值分别降低43%、34%与22%,各时刻对应幅值如表7所示。

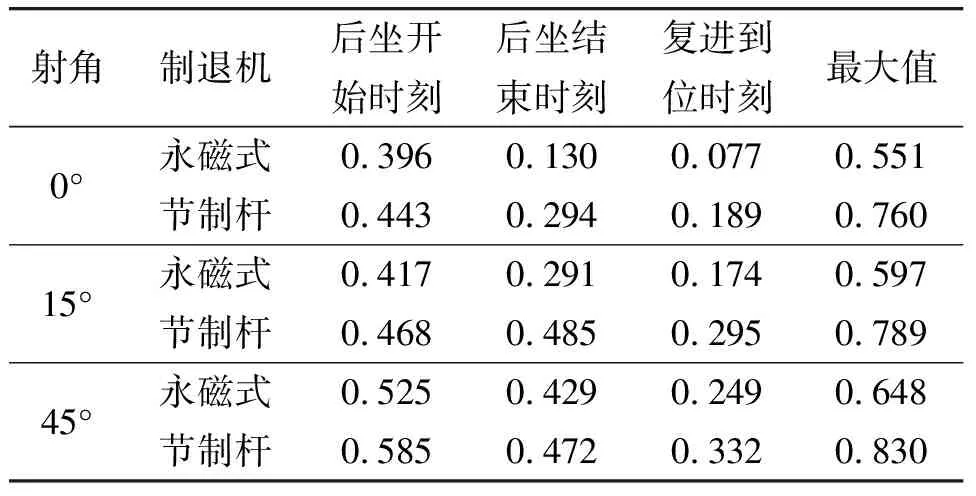
表7 炮口垂直方向位移幅值变化情况 mm

4.2 耳轴载荷情况

对0°、15°和45°射角工况下的耳轴载荷进行提取,得到如图11～13所示的耳轴所受力矩变化。由图11～13可知,耳轴处所受力矩在射击开始后迅速增大,并以振荡形式逐渐减小,最终回归至0左右。在0°、15°与45°的不同射角下,与采用节制杆制退机相比,采用永磁式制退机时耳轴所受最大力矩分别降低29%、31%与33%,力矩波动范围分别缩减23%、26%与25%,耳轴所受力矩情况如表8所示。

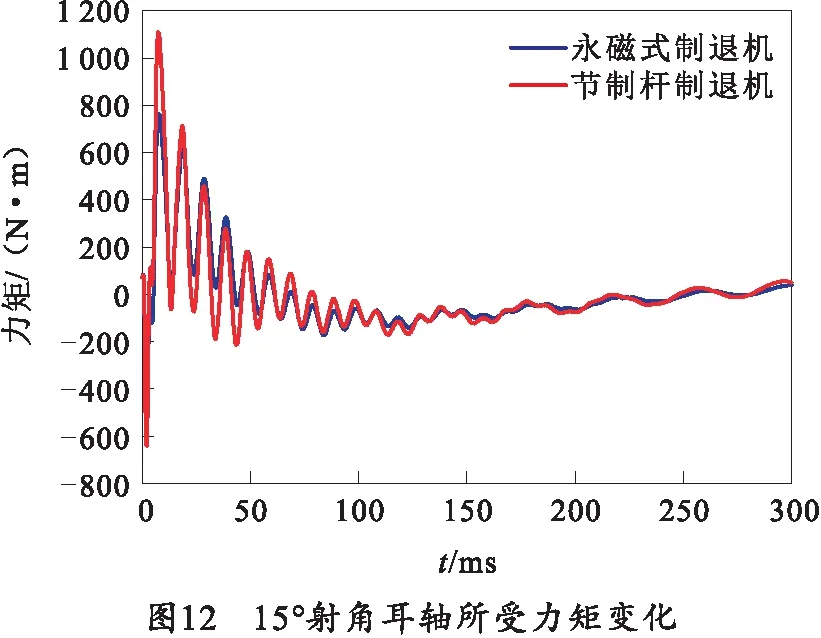
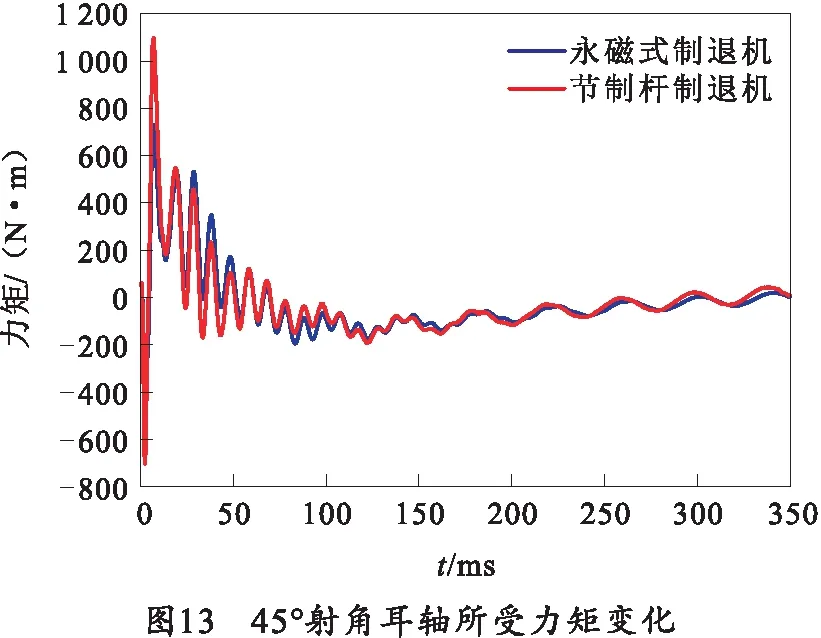
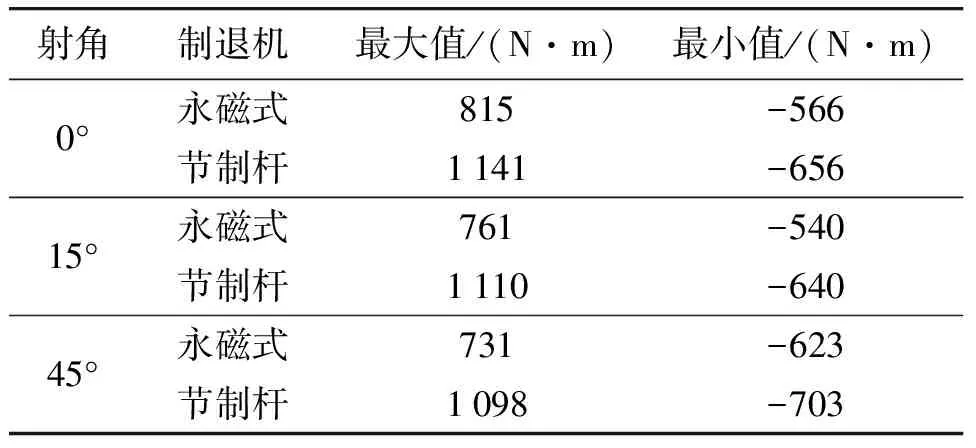
表8 耳轴所受力矩情况

5 结论

通过对某口径火炮的后坐复进运动进行分析,发现在相同的运动位移与时间下,永磁式制退机力的平台效应更加显著;通过刚柔耦合动力学仿真对采用永磁式制退机与原节制杆制退机下的炮口位移与耳轴载荷变化情况进行了分析,得到如下结论:

1)相同发射载荷下,永磁式制退机对炮口位移的影响更小,在0°、15°与45°的射角下,炮口振动幅值分别降低43%、34%与22%。

2)与采用节制杆制退机相比,永磁式制退机工况耳轴的受扭情况更优,在0°、15°与45°的射角下,耳轴处所受力矩峰值分别降低29%、31%与33%,力矩波动范围分别缩减23%、26%与25%。

因此,永磁式制退机对炮口位移和耳轴载荷的影响更小,有利于改善火炮的动态特性。