经纬仪炮膛水平穿线的切点位置估计法
2023-04-28霍李王媛高洪飞凌山珊
霍李,王媛,高洪飞,凌山珊
(中国人民解放军63853部队,吉林 白城 137001)
在火炮检测中,零线检查[1-2]、管间平行度[1,3]和炮轴一致性[4]等检测项目需要炮膛轴线对准靶板上对应的瞄准十字线竖线。通常是在火炮和靶板之间架设经纬仪,先进行经纬仪炮膛穿线使得经纬仪视轴与炮膛轴线所在的铅垂面重合,然后进行放线使得经纬仪瞄准靶板上对应的瞄准十字线,从而实现炮膛轴线对准靶板上对应的瞄准十字线竖线。另外,在炮膛轴线偏离射面的偏离角[1,4-6]、火炮俯仰半径[6]、瞄准线偏移量[1,7-8]、调炮精度[9-12]、火炮耳轴调平[13]、火炮回转中心位置标定[14]等检测项目中都是以穿线后的经纬仪视轴所在的铅垂面作为观测基准。因而,提高经纬仪炮膛穿线的精度和效率,对火炮的试验鉴定具有现实意义。
在实际操作中,通常以炮口端面中心和炮尾击针孔中心分别为炮膛轴线在炮口和炮尾的标记点,以这两个标记点的连线作为炮膛轴线。由于在穿线的过程中往往需要多次转动经纬仪和火炮的水平方向,而在火炮方向转动时,炮膛轴线上前后两个标记点的位置也会随之发生变化。这给穿线带来了困难,特别是在火炮回转轴与身管前后两个观瞄点距离相近的情况下尤其困难,甚至会出现不能实现穿线的情况。
笔者在分析经纬仪炮膛穿线实质的基础上,先估计出穿线完成后经纬仪应瞄准点的位置,再通过经纬仪对准该估计点,从而实现穿线。采用蒙特卡洛方法对穿线过程进行模拟,比较传统方法和本文方法的差异,为现场实施提供思路,为国家军用标准修订提供依据。
1 传统的经纬仪穿线法
1.1 传统方法
在距炮口正前方约两倍炮身长的位置上架设经纬仪并整平,转动火炮方向机和经纬仪,使炮口十字线、膛内分划环十字线(或击针孔中心点)同经纬仪十字线相重合[1]。图1为穿线的水平投影示意图,点O为火炮回转轴在水平面上的投影点(称为火炮回转中心),点T为经纬仪三轴中心在水平面上的投影点,点A为炮口端面中心(称为炮口标记点),点B为炮尾端面中心(称为炮尾标记点)。点A、B的连线AB为炮膛轴线。通常情况下点A、B、T三点不共线,穿线的目的是使得这三点共线。

传统的穿线方法是:经纬仪瞄准炮尾标记点B;转动火炮方向,使炮口标记点A被经纬仪瞄准;调整经纬仪望远镜焦距,观察炮尾标记点B是否被经纬仪瞄准;如果瞄准则完成穿线,如果未瞄准,则转动火炮方向使经纬仪瞄准炮尾标记点B;重复上述操作,直到只调整经纬仪望远镜焦距,就可瞄准两个标记点,便实现穿线。
1.2 传统方法的问题
在穿线的过程中,除了经纬仪点T的位置是不变的外,两个标记点A和B的位置是不断变化的,往往需要反复转动经纬仪和火炮方向机,通过逼近的方式使得这三点近似共线。
当火炮回转轴与身管前、后两个标记点的距离相近时(即lOA≈lOB),逼近效果不明显,甚至可能会出现不能穿线的情况,如图2所示。

2 经纬仪火炮穿线的实质
设火炮回转中心点O与炮膛轴线AB的垂线为OC,垂点为点C,火炮回转轴到炮膛轴线的水平距离为lOC。设穿线完成后,炮口标记点的位置为点Aq,炮尾标记点的位置为点Bq,则点Aq、Bq、T三点共线,如图3所示。
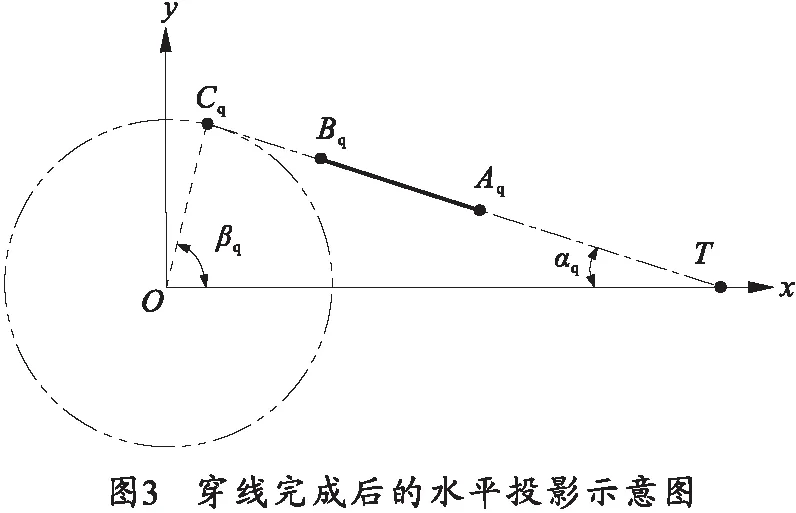
在图3中,经纬仪三轴中心点T到火炮回转中心点O的距离为lOT。则以点O为圆心、以lOC为半径的圆,与直线AqBq相切,切点为点Cq。
对给定的待测火炮来说lOCq是固定值,经纬仪布置完成后点T也固定的,因而切点Cq的位置也是固定的。只要转动火炮方向机,使垂点C与切点Cq重合,就实现了穿线。因此,穿线的实质就是使经纬仪瞄准切点Cq。
3 切点位置估计法
对具体的测量实施来说,切点的位置是固定的。如果在穿线前,能确定切点Cq的位置,经纬仪将切点Cq瞄准,转动火炮方向机使得点A或点B处于经纬仪视轴上,即可实现穿线。
如图3所示,如果能准确测量lOT和lOC,就可以算出角αq的值,即αq=arcsin(lOC/lOT)。从而在现场可使经纬仪将切点Cq瞄准,转动火炮方向机实现穿线。但是在现场,由于火炮回转轴的位置未知,并且很难准确找到垂点C的位置,因而该思路实施困难。
笔者提出了一种切点位置估计法。如图4所示,大致估计出垂点C的位置,测量两端标记点的距离lAB、炮口标记点A与垂点C的距离lAC,以及炮尾标记点B与垂点C的距离lBC。第i次转动火炮时,通过经纬仪瞄准炮身两端面标记点Ai和Bi可得到水平观测角分别为αAi和αBi,令θAiBi=αAi-αBi。估算出经纬仪瞄准点Ci对应的水平观测角αCi:
αCi=αBi-θAiBilBC/lAB.
(1)

具体穿线过程如下:
步骤1大致估计垂点C的位置,测量lAB、lAC和lBC。
步骤2调整经纬仪望远镜和火炮身管水平方向转动,使经纬仪望远镜能够观察到炮身两端的标记点。
步骤3保持火炮不动,经纬仪瞄准炮身两端标记点A0和B0可得到水平观测角分别为αA0和αB0。
步骤4按式(1)估算出经纬仪瞄准点C0对应的水平观测角αC0,将经纬仪转到该水平角位置。
步骤5保持经纬仪不动,第i次转动火炮方向机,使得经纬仪瞄准炮口标记点Ai。
步骤6保持经纬仪和火炮方向都不动,调整经纬仪望远镜焦距观察炮尾标记点Bi,判断点Bi是否被经纬仪瞄准。如果瞄准,则完成穿线;如果未瞄准,则重复步骤3~6。
4 模拟分析
4.1 数学解算
4.1.1 穿线完成后的点坐标解算
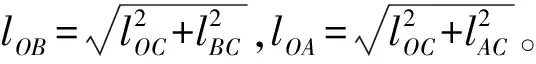
(2)
切点Cq的相对坐标(xCq,yCq)为
(3)
炮口标记点Aq(xAq,yAq)的相对坐标为
(4)
炮尾标记点Bq(xBq,yBq)的相对坐标按式(4)的规律解算。
设穿线完成后,OAq连线与x轴的夹角为βAq,则
(5)
OBq连线与x轴的夹角为βBq,可按式(5)的规律解算βBq。
4.1.2 可观测的极限位置解算
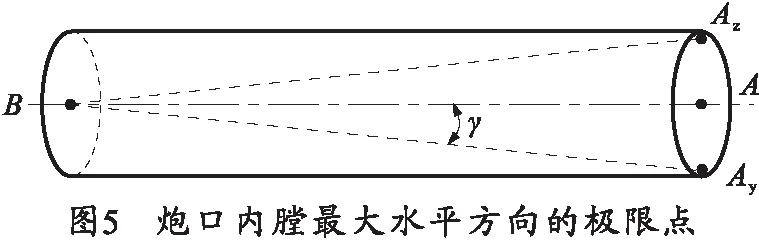
由于身管口径r的存在,在炮口端面处,最大水平方向有2个极限点,即按身管射击方向分为左极限点Az和右极限点Ay,如图5所示。直线AzB和直线AyB与炮膛轴线AB的夹角均为
γ=arctan(0.5r/lAB).
(6)
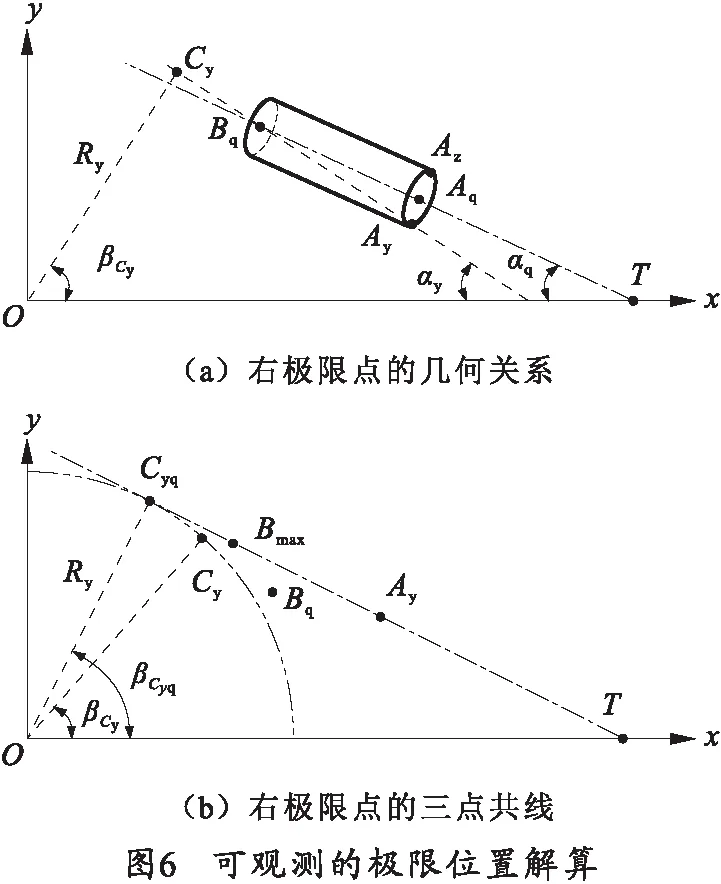
在图6(a)中,以右极限点Ay为例,穿线完成时,直线AyBq与x轴的夹角为αy,则
αy=αq+γ.
(7)
在图6(a)中,过点O作直线AyBq的垂线,垂点为点Cy,则点Cy的坐标(xCy,yCy)为
(8)
点O到直线AyBq的距离Ry为
(9)
直线OCy与x轴的夹角为
(10)
如图6(b)所示,转动火炮方向机,使得经纬仪能同时瞄准点Ay、Bmax,即点Ay、点Bmax与点T三点共线。此时点Cy绕点O逆时针旋转到点Cyq,旋转角为Δβmax=βCyq-βCy,其中βCyq为直线OCyq与x轴的夹角:
βCyq=arccos(Ry/lOT).
(11)
此时,点Bq绕点O逆时针旋转的极限位置为点Bmax。直线OBmax与x轴的夹角为
βBmax=βBq+Δβmax.
(12)
同理,可以计算出左极限点Az对应的βCz和βCzq,以及点Bq绕点O顺时针旋转的极限位置点Bmin。直线OBmin与x轴的夹角为
βBmin=βBq-Δβmin,
(13)
式中,Δβmin=βCz-βCzq。
4.1.3 炮身初始位置设定
设i为转动火炮的次数,当i=0时,为火炮准备好待穿线的初始状态。在点Bmin与点Bmax之间的圆弧上随机选取一点B0作为炮尾端观测点的初始位置。设直线OB0与x轴的夹角为βB0,直线OA0与x轴的夹角为βA0,则
(14)
式中,k为[0,1]内均匀分布的随机值。
将lOA、βA0和lOB、βB0分别代入式(3),可分别计算出炮身两端标记点的初始坐标点A0(xA0,yA0)和点B0(xB0,yB0)。
4.1.4 考虑瞄准误差的穿线
通过经纬仪望远镜能观察炮身前后十字线产生的方向瞄准随机误差为σJ。以预瞄准点Bi为例,实际瞄准线却过点B′i,如图7(a)所示。
在图7(a)中,线段BiB′i与直线TBi垂直,其长度为σJ。点B′i的坐标(xB′i,yB′i)为
(15)
式中,(xBi,yBi)为预瞄准点Bi的坐标;αBi为直线TBi与x轴的夹角,
αBi=arctan[(yBi-yT)/(xT-xBi)].
(16)
经纬仪视轴TB′i与x轴的夹角为α′Bi,可通过点B′i(xB′i,yB′i)、T(lOT,0)的坐标,按式(16)的规律解算。
如图7(b),如果瞄准炮口标记点时没有误差,则第i次转动火炮方向机,炮口标记点将与经纬仪视轴TB′i相交于点A′Bi。βA′i为直线OA′Bi与x轴的夹角,则
(17)
将lOA、βA′i代入式(3),可计算出点A′Bi的坐标(xAB′i,yAB′i)。
考虑到瞄准误差时,第i次转动火炮方向机后,炮口标记点的实际位置点Ai+1的坐标为(xAi+1,yAi+1)。过点A′Bi作直线TB′i的垂线A′BiA″i,与直线TAi+1相交于点A″i,线段A′BiA″i的长度为σJ,则可由点A′Bi的坐标、角α′Bi,按式(15)的规律计算点A″i的坐标。
按上述规律可计算出炮口标记点转到实际位置点Ai+1的坐标,以及对应的炮尾标记点的实际位置点Bi+1的坐标。
4.1.5 考虑瞄准误差的垂点位置估计
预瞄准点Ai,按式(15)的规律得到点A′i的坐标(xA′i,yA′i)。将点A′i、B′i的坐标代入式(18)解算出θA′iB′i=∠A′iTB′i。
(18)
将lAB、lBC、αBi、θA′iB′i代入式(1),估算出考虑瞄准误差时经纬仪瞄准点Ci对应的水平观测角α′Ci。
用α′Ci代替α′Bi,按前述规律计算出点Ai+1和点Bi+1的坐标。
4.1.6 炮口标记点到经纬仪视轴的距离
设穿线完成后的经纬仪视轴为TBq,过点Bq(xBq,yBq)和点T(xT,yT),其方程为ax+by+c=0。
第i次转动火炮方向机后,炮口标记点Ai(xAi,yAi)到直线TBq的垂点为ATi(xATi,yATi),则
(19)
式中,a=(yT-yBq)/(xT-xBq),b=-1,c=yT-a。
炮口标记点Ai到直线TBq的距离li为
(20)
4.2 蒙特卡洛方法实施步骤
步骤1穿线完成后的点坐标解算。按4.1.1节解算出给定条件下,穿线完成后点Aq(xAq,yAq)、Bq(xBq,yBq)、Cq(xCq,yCq)的坐标。
步骤2可观测的极限位置解算。按4.1.2节解算出给定条件下,经纬仪望远镜能观察到的炮身后端点B的2个极限位置点Bmin、点Bmax对应的夹角βBmin、βBmax。
步骤3炮身初始位置设定。按4.1.3节,在Bmin和Bmax之间的圆弧上随机选取一点B0作为炮身后端观测点,并计算出对应点A0的位置。
步骤4计算炮口标记点到经纬仪视轴的距离。传统方法按4.1.4节解算出实际位置点Ai的坐标,本文方法按4.1.5节解算出实际位置点Ai的坐标,并按4.1.5节解算出第i(i=0,1,2,…,n)次转动火炮后,炮口标记点Ai到直线TBq的距离li。
步骤5重复步骤3~4的过程m次,分别得到传统方法和本文方法在第i次转动火炮后的距离lij,其中i=0,1,…,n;j=0,1,…,m。对结果进行统计,得到第i次转动火炮后的炮口偏离均方差
(21)
4.3 比较分析
4.3.1 基本条件
基本条件:lAB=5 m;lAC=4 m;lOT=3lAB;lOC=500 mm;r=150 mm;通过经纬仪观测竖线的标准差σJ=0.2 mm;lAB的测量标准差σlAB=2 mm;lBC的估计标准差σlBC=50 mm。
k=lAC/lAB,为垂点C与炮尾标记点B的重合度。当k=1时,垂点C与炮尾标记点B的位置重合;当k≠1时,垂点C与炮尾标记点B的位置偏离;当k=0.5时,垂点C正好为炮身两端标记点A与B的中点。基本条件中,k=0.8。
随机抽样m=100 000次,得到的结果δli如表1所示。当δli≤σJ时,实现穿线。
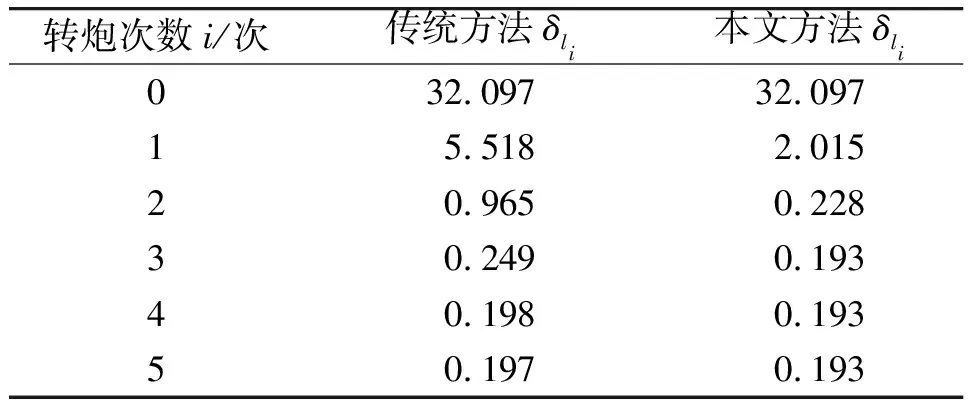
表1 基本条件下得到的δli对比 mm
从表1可以看出:在前2次转动火炮时,传统方法和本文方法都迅速收敛,但本文方法的收敛效果更好;转动火炮3次时,本文方法就能实现穿线;而传统方法需要转炮4次时才能实现穿线。
4.3.2 经纬仪观测竖线的标准差
在基本条件的基础上,分别取经纬仪观测竖线的标准差σJ为不同值时得到的炮口偏离均方差δli,结果如表2所示。
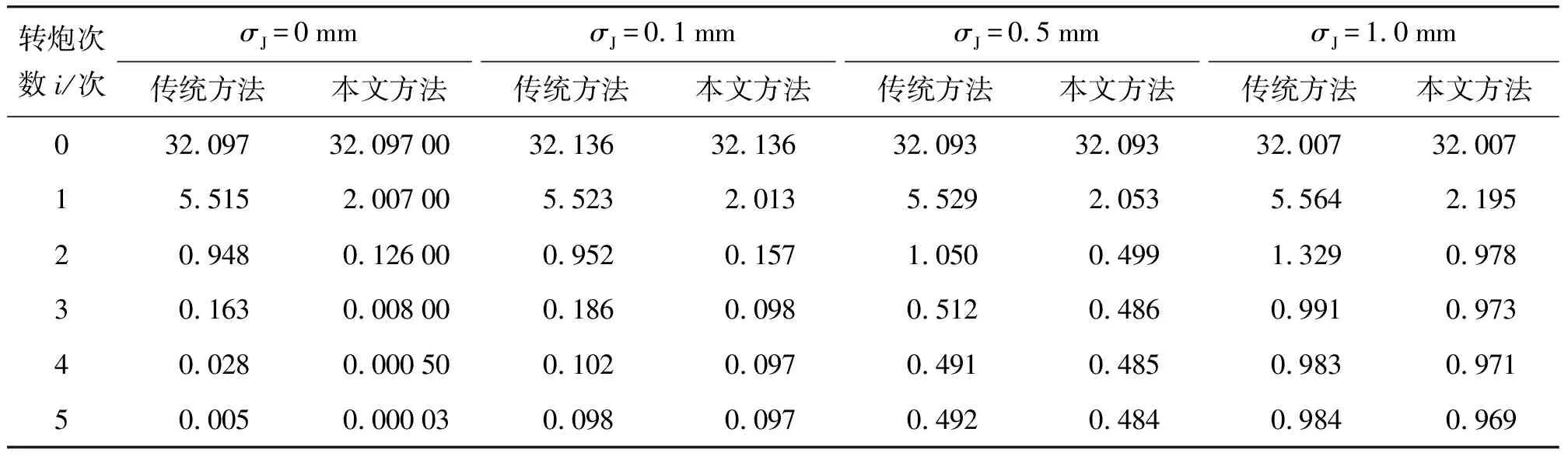
表2 经纬仪观测竖线的标准差σJ对δli结果的影响 mm
从表2可以看出:在最初的2次转动火炮时,传统方法和本文方法都迅速收敛,但本文方法的收敛效果更好;要实现δli≈σJ,传统方法一般需要转动火炮4次,而本文方法需要3次甚至2次就能达到要求,实现穿线。
4.3.3 垂点与炮尾标记点的重合度k
当k≈0.5时,传统方法收敛缓慢,甚至不能收敛,这验证了1.2节的观察结果;而本文方法不受其影响,转动火炮4次就能实现穿线。
在基本条件的基础上,取k为不同值时,得到的炮口偏离均方差δli,结果如图8所示。从图8可以看出:两种方法在k=1处的结果都最小;在k≈1时,传统方法比本文方法具有优势,甚至可以在只转动火炮1次的情况下就实现穿线;当k值偏离1越远,本文方法越有优势。

4.3.4 火炮回转轴到炮膛轴线的水平距离lOC
在基本条件的基础上,分别取火炮回转轴到炮膛轴线(或基准管轴线)的水平距离lOC为不同值时,得到的炮口偏离均方差δli,如表3所示。
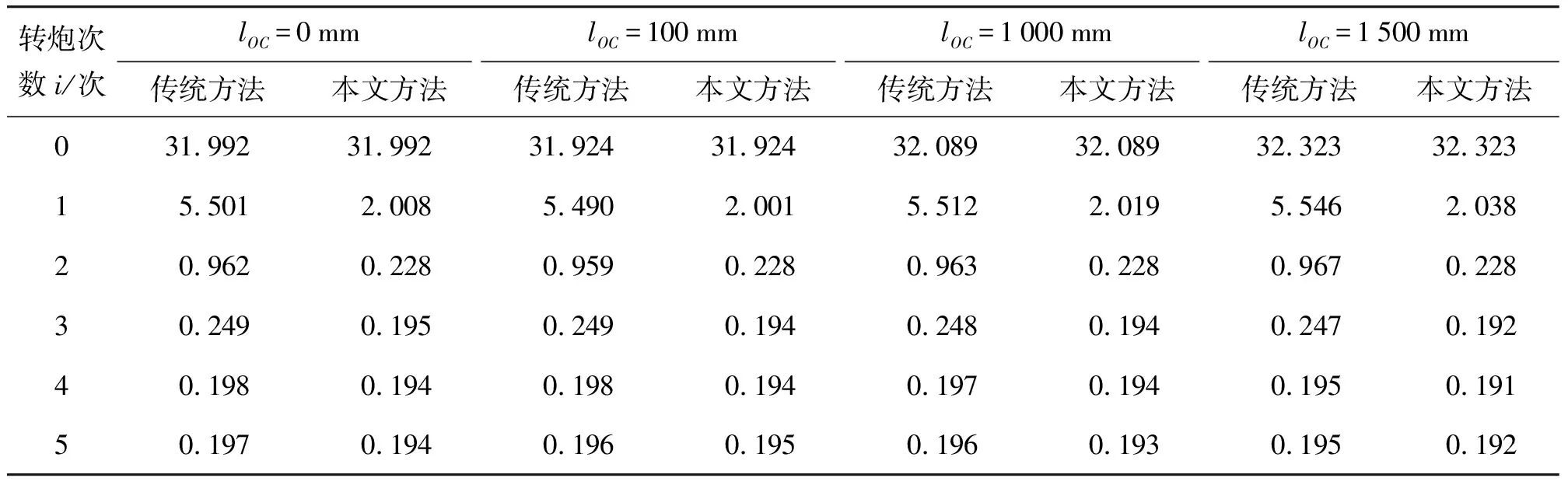
表3 火炮回转轴到炮膛轴线的水平距离lOC对δli结果的影响 mm
从表3可以看出,对同一种方法来说,lOC的大小对结果无显著影响。
4.3.5 测量标准差σlAB
在基本条件的基础上,取炮身两端标记点距离的测量标准差σlAB为不同值时,用本文方法得到的结果测量均方差δli,结果如表4所示。从表4可以看出:在σlAB≤10 mm范围内,σlAB对本文方法的结果δli无显著影响。
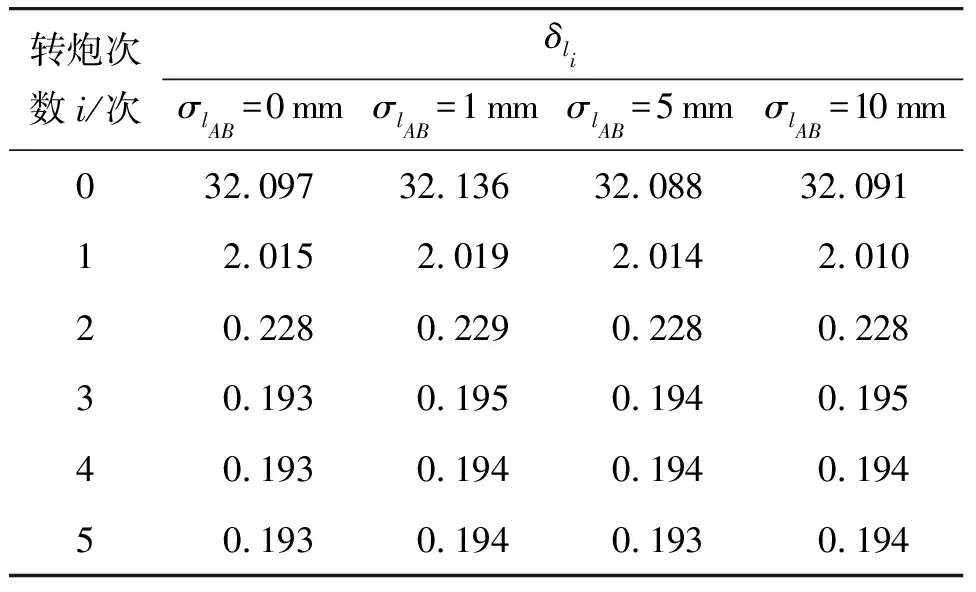
表4 测量标准差σlAB对δli的影响 mm
4.3.6 估计标准差σlBC
在基本条件的基础上,取炮尾标记点到垂点估计位置的距离lBC的标准差σlBC为不同值时,用本文方法得到的结果测量均方差δli,结果如表5所示。

表5 估计标准差σlBC对δli的影响 mm
从表5可以看出:在估计标准差σlBC≤100 mm的范围内,σlBC对结果无显著影响。
5 结束语
笔者提出的穿线方法,现场实施条件宽泛,具有普适性,通常只需转动火炮2~3次就能实现穿线,优于传统方法。特别是在火炮回转轴与身管前、后两个标记点的距离相近时,要避免采用传统方法穿线。与本文方法相比,传统方法只有在垂点与炮尾标记点的位置近似重合的情况下,才具有优势。
