谈数学概念深度教学的策略

印俊秀

摘 要：“深度”是数学教学的应然追求.唯有深化概念教学，通过深度教学深化学生理解、发展学生能力，才能从根本上提高学生的数学素养.有深度的数学概念教学应基于学生兴趣追问“知识从何而来”，基于深度理解探寻“知识的本质是什么”，基于高阶思维考量“知识去向何方”.数学概念深度教学呼唤着教师的深度探索.

关键词：深度教学；数学概念；平方差公式

1 提出问题

数学概念是在数学家反复实践与检验的基础上生成的，是构成数学知识的细胞.毋庸讳言，数学概念确实对学生数学知识结构的形成和发展十分重要，但在教学实践中，笔者发现一些教师的概念教学往往是浮光掠影，学生对数学概念的理解呈现出一种浅层化、模糊性的状态.事实上，唯有通过深化概念教学来深化学生理解、发展学生能力，才能从根本上提高学生的数学素养［1］.

如何实现概念深度教学？首先，教师需站在一个较高的层面上研究概念本身，并引领学生思考学习这个概念的原因、这个概念产生的缘由、生成的过程及与其他概念间的联系等问题，从本质上来说就是师生共同经历概念产生和发展的曲折过程，通过不断介入概念的过程因素和实践因素深化对概念的认识和理解，此时还是渗透数学文化元素的好时机.其次，在理解上述问题之后，可以通过不断介入理论因素、结果因素和证实因素，引领学生理清概念的结果，学会用数学概念解决数学问题和实际问题.最后，自然需要引导学生进一步思考概念的去向，即还能衍生出哪些新概念、新知识，这里借助猜想、证伪、证实等方法的指引可以培养学生思维的反思性、批判性和创造性.下面笔者结合“平方差公式”的概念教学，实现概念深度教学上的融会贯通.

2 数学概念深度教学策略

2.1 基于学生兴趣追问“知识从何而来”

想要促成概念教学中稳定、清晰的认知结构，首先需要明晰本节课前后概念间的逻辑体系，切实理清概念的来处.在课堂导入环节基于学生的兴趣追问“知识从何而来”，对于学生思维的唤醒、情感的深度发展具有一定的意义.这就需要教师在教学设计时整体分析和思考教学内容，这样才能在课堂导入环节以主导者的角色引领学生深入思考概念本身，以启发学生思维［2］.

片断1：温故知新导入概念

问题1：整式乘法中的多项式乘法法则是什么？请试着用不同的表达方式阐述.（学生分别从文字语言和符号语言展开描述）

追问：那这样的多项式相乘后展开都有四项吗？

问题2：数学在古希腊人的心目中是神奇的，他们对数学十分重视，也研究出很多计算技巧.下面揭示其中的一种方法：a²=（a+b）（a-b）+b².例如：297²=（297+3）×（297-3）+3²=300×294+9=88 209.你能试着用这种算法验算9²、15²、28²、99²吗？从中你能发现哪些规律？

以上案例中，教师以问题引领学生回顾多项式乘法法则和体验古希腊人计算的技巧，尽管设问的方式不同，但在激活已有认知、引发学生兴趣上效果明显.事实上，正是因为教师恰如其分地导入，才实现了知识的正向迁移；也正是因为教师恰到好处地抛出了一个有趣的算法，才引发了探索与发现，最终实现了高阶思维的自然发展.

2.2 基于深度理解探寻“知识的本质是什么”

从教育教学角度可以发现，教师在教学中最关心且投入时间最久的环节就是探寻“知识的本质是什么”.真正理解数学概念就是要理解概念的本质、类属及与其他概念间的联系，这个过程也是学生顺应新概念的过程.如果说在概念导入阶段教师已然引领学生建立起了新旧概念间的联系，那么深度理解就需要学生在教师的引导下自主探究，从而切实理解和掌握概念本质.

片断2：在自主探究中获得公式

此时，在教师的引导下，学生很快自主归纳得出公式：a²-b²=（a+b）（a-b）.

问题3：这个式子可以推导得出吗？（学生展示方法，继而，在教师的点拨下学生归纳得出了平方差公式，即（a+b）·（a-b）=a²-b².

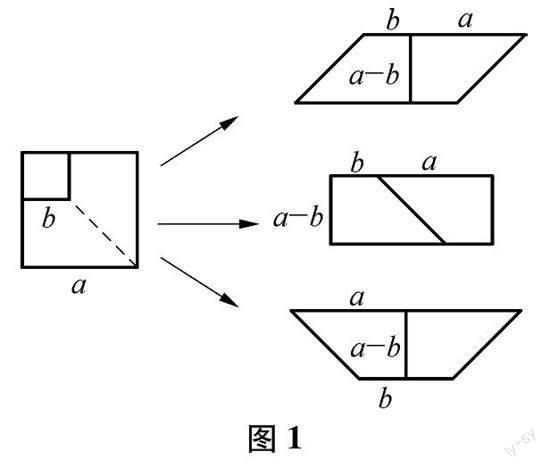
问题4：我们在“数”的角度完成了公式的推导，那下面是不是该从“形”的角度予以验证？哪里可以得出图形呢？（师生再一次共同探索，通过构造与公式相关几何图形的面积，并在GeoGebra软件下拼图，最终生成了图1所示的3种验证方法）

在教材内容结构的基础上以问题引领学生运用多项式乘法法则计算，并从“数”与“形”这两个角度着手推导和验证平方差公式，再以信息技术为辅助，给予学生多感官的刺激与体验，让学生在切身感受中深化对公式本身的理解和认识.这样的过程，不仅让学生自主获得了数学知识，还自然而然地渗透了数学思想方法，使深度教学真正指向了深度理解和创新意识.

3 基于高阶思维考量“知识去向”

深度教学理念下的概念教学并非追寻概念的深度与难度，很大程度上应是让学生在体验数学概念的过程中理解概念、建构概念、促进知识和经验的生成，发展学习力和数学核心素養.这就需要用有效的概念应用环节促使学生思维的进阶，用有效的课堂小结引领学生走向知识的更远处和思维的更深处，使知识的去向一目了然.

片断3：在概念应用中进阶思维

练习1 辨析（a+b）（a-b）=a2-b2，并分别圈出以下式子中的a和b.

（1） （x+1）（x-1）；

（2） （-x+3）（-x-3）；

（3） （2x-3y）（2x+3y）；

（4） （0.2a+1）（1-0.2a）；

（5） （x+y+z）（x+y-z）.

练习2 用平方差公式计算：

（1） （2x+1）（2x-1）；

（2） 102×98；

（3） （y+2）（y-2）-（y-1）（y+5）.

练习3 阅读材料并解决问题.

计算（2+1）（2²+1）（2⁴+1）（2⁸+1）时，东东发现适当变式原式即可出现特殊的结构，再应用平方差公式解决就简单多了.

这里练习1和练习2则是对学生公式直接应用、简化应用等的考查.而练习3具有较强的综合性且阅读信息量大，因此教师通过微课视频展示的方法，为学生更深层次理解平方差公式和更加娴熟地运用平方差公式提供辅助，同时适时地插入视频，让原本沉寂的课堂瞬间活跃起来，更重要的是为学生问题的解决适切搭建了思维的脚手架，让学生一步步地走向思维的深处.整个过程中，师与生、生与生深度交流，共同实现了思维的进阶.

片断4：在课堂小结中走向知识的更远处

问题5：请大家对今天所学的内容谈谈收获与疑惑.

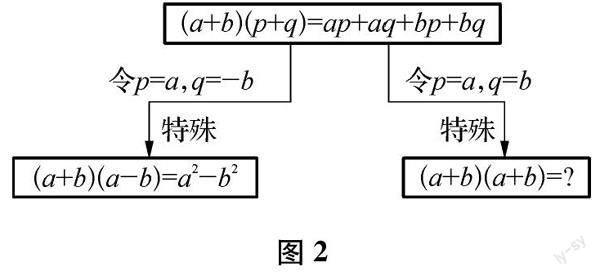
问题6：如图2，你还想探索什么问题？

追问：据a2-b2=（a+b）（a-b），你还能想到什么问题？可以从“形”的其他角度验证平方差公式吗？你能根据“雪球效应”自主编制习题并解决吗？这个问题就留到课后，下节课我们一起再来研究.

将课堂延展到课后，让学生深度思考“知识去向何处”，这样不仅可以促成完整的教学过程，还能引发学生的想象思维，让学生张开想象的翅膀，实现深度学习.

总之，深度教学模式不仅指向教师深度的“教”，还指向学生深度的“学”.在数学概念教学中，当教师深入解读概念本身，直面研究概念时，当教师意识到概念教学设计需基于学生立场时，当学生的认知结构和思维水平通过概念习得发生改变时，数学深度概念教学才真正发生，才真正意义上达到了深度教学的目的.

参考文献：

［1］ 马华平.核心问题引领，在深度學习中逼近数学本质［J］.数学教学通讯，2019（16）：4748.

［2］ 翟丽萍，吴登文.数学概念深度教学的情境创设策略［J］.小学数学教育，2016（19）：1718.