用单摆测定重力加速度实验要点评析

■山东省沂源县第一中学 杨成柱

用单摆测定当地的重力加速度是力学中的一个重要实验。用单摆测定重力加速度的原理:当摆角较小时,单摆做简谐运动,其运动周期,则,因此只要测出单摆的摆长l和周期T,就可以求出当地的重力加速度g的值。下面就这个实验中的要点做详细说明,供同学们参考。

一、单摆的制作

选用密度大、体积小的金属小球,长度约为1 m 的不可伸长的轻细线,将细线穿过金属小球上的小孔,做成单摆。

二、单摆的摆动

金属小球摆动时,摆线与竖直方向间的最大夹角不要超过5°,因为只有金属小球做小角度摆动时,单摆的周期公式才成立;同时,应保持金属小球在竖直面内摆动,而不能摆成圆锥摆。

三、摆长、周期的测量

摆长等于摆线长与摆球半径之和,用毫米刻度尺量出摆线长度l',用游标卡尺测出摆球的直径d,即可计算出摆长。

单摆的周期是摆球完成一次全振动所用的时间。在测量周期时,从摆球到达平衡位置开始计时,先测出单摆完成30 次或50 次全振动所用的总时间t,再计算出单摆的周期T,可以有效减小实验误差。

四、数据处理

1.公式法:先测出摆长l,并利用求出周期,再利用公式求出重力加速度。

2.图像法:根据测出的多组摆长l和对应的周期T,作l-T2(T2-l)图像,根据单摆周期公式得,因此l-T2(T2-l)图像应是一条过原点的直线。如图1所示,求出过原点倾斜直线的斜率k,即可利用g=4π2k求出重力加速度。

例1(2022年高考上海卷)在“用单摆测定当地的重力加速度”的实验中:

(1)摆线质量和摆球质量分别为m线和m球,摆线长为l,摆球直径为d,则( )。

A.m线≫m球,l≪d

B.m线≫m球,l≫d

C.m线≪m球,l≪d

D.m线≪m球,l≫d

(2)小明在测量后作出的T2-l图像如图2所示,则他测得的结果是g=_____m/s2。(保留2位小数)

(3)为了减小实验误差,判断应该从最高点还是最低点开始计时,并简述理由。

解析：(1)单摆模型要求用轻细线悬挂小球,不计细线质量,将摆球视为质点,因此该实验要求摆线质量远小于摆球质量,摆线长度远大于摆球直径,即m线≪m球,l≫d。

(3)因为摆球摆动到最低点时的速度达到最大,所以从最低点开始计时,误差最小。

答案：(1)D (2)9.74 (3)应从最低点开始计时,因为摆球摆动到最低点时的速度最大,计时误差最小。

命题意图：本题考查用单摆测定重力加速度实验对装置的要求,以及用图像法处理实验数据的能力和误差分析的能力。

例2在“用单摆测定当地的重力加速度”的实验中:

(1)利用如图3所示的方式测量摆长,若测出单摆的周期为T、摆线长为l、摆球直径为d,则当地的重力加速度g=____(用测出的物理量表示)。

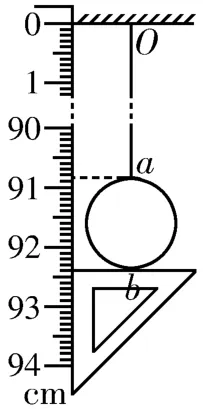
图3

(2)某同学用一个铁锁代替小球做实验。只改变摆线的长度,测量了摆线长度分别为l1和l2时单摆的周期为T1和T2,则当地的重力加速度g=____(用测出的物理量表示)。

(3)另一位同学在利用如图3所示装置测量摆长l时,每次都在小球运动到最低点b时取数,然后测量了多组实验数据作出了T2-l图像,则他得到的图像最有可能是图4中的( )。

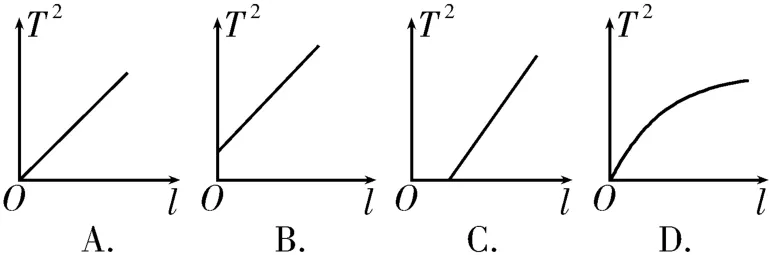
图4

解析：(1)根据单摆的周期公式T=,解得。

(2)设摆线下端到锁的重心的距离为x,根据单摆的周期公式得,解得。

(3)设小球的半径为r,根据单摆的周期公式,解得,因此他得到的T2-l图像最有可能是图4 中的C。

答案：(1)

命题意图：本题考查用单摆测定重力加速度的实验原理,以及用图像法处理实验数据的能力。

例3用单摆测定当地的重力加速度的实验装置如图5所示。

(1)下列对测量原理的理解中正确的是____。

A.由g=a可知,周期T一定时,重力加速度g与摆长l成正比

B.由g=a可知,摆长l一定时,重力加速度g与周期的平方T2成反比

C.单摆的周期T和摆长l可用实验测定,由可算出当地的重力加速度

(2)若测量得到的g值偏大,则可能是因为____。

A.组装单摆时,选择的摆球质量偏大

B.测量摆长时,将摆线长当成了摆长

C.测量周期时,把n次全振动误认为是(n+1)次全振动

(3)表1是某同学记录的实验数据,并做了部分处理。

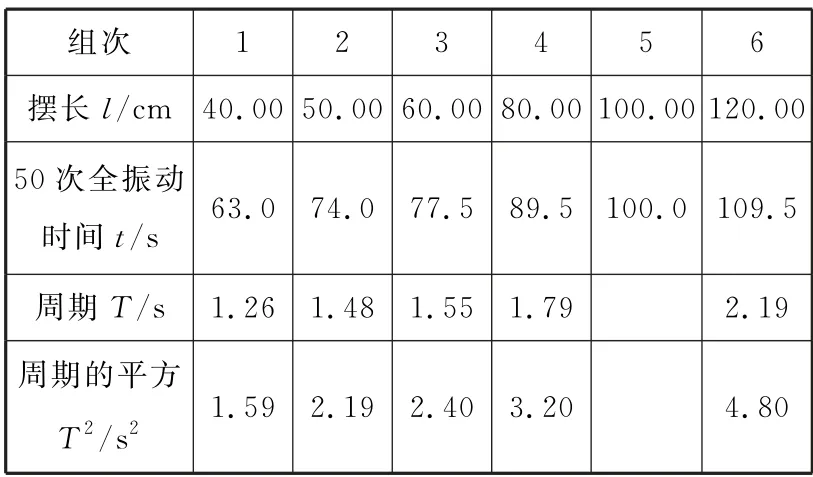
表1

请计算第5组实验中的T2=____s2。

(4)将表1中的数据输入计算机,可得到如图6所示的l-T2图像,倾斜直线经过坐标原点,斜率k=0.25。由此求得当地的重力加速度g=____m/s2。(取π2=9.87,结果保留3位有效数字)

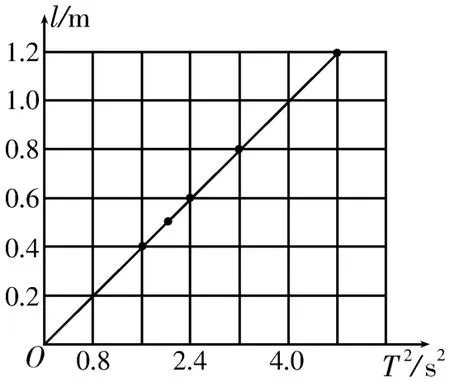
图6

解析：(1)重力加速度与单摆的摆长和周期均无关,选项A、B 错误。根据单摆的周期公式,测出单摆的摆长l与周期T,可以算出当地的重力加速度,选项C正确。

(3)根据表1中的数据可知,第5组实验中完成50次全振动所用的时间为100.0 s,则单摆的周期T=2.0 s,因此T2=4.00 s2。

答案：(1)C (2)C (3)4.00 (4)9.87

命题意图：本题考查用单摆测定重力加速度的实验原理,误差分析的能力,以及用图表法和图像法处理实验数据的能力。

1.在用单摆测定当地的重力加速度的实验中,根据多组实验数据作出T2-l图像,可以求出重力加速度g。已知某次实验中三位同学作出的T2-l图像如图7中的a、b、c所示,其中直线a和b平行,直线b和c都过原点,直线b对应的g值最接近当地重力加速度的值,则相对于直线b,下列判断中正确的是( )。

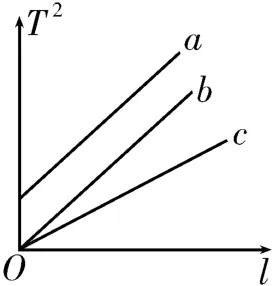
图7

A.出现直线a的原因可能是误将悬点到摆球上端的距离记为摆长l

B.出现直线c的原因可能是误将49 次全振动记为50次全振动

C.直线c对应的g值小于直线b对应的g值

D.直线a对应的g值等于直线b对应的g值

2.用如图8所示的实验装置做“用单摆测定当地的重力加速度”实验。

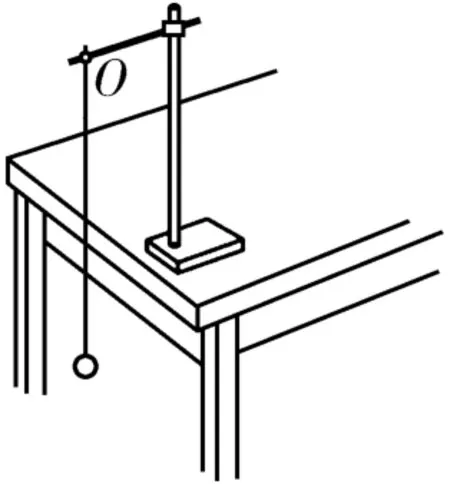
图8

(1)为了减小测量误差,下列说法中正确的是_____。

A.将钢球换成塑料球

B.从摆球经过平衡位置时开始计时

C.把摆球从平衡位置拉开一个很大的角度后释放

D.记录一次全振动的时间作为周期,根据公式计算重力加速度g

(2)某同学用质量分布不均匀的球体作摆球测定当地的重力加速度,摆球的重心不在球心,但是在球心与悬点的连线上。他仍将从悬点到球心的距离当成摆长l,通过改变摆线的长度,测得6组l和对应的周期T,画出T2-l图像如图9所示,然后在直线上选取A、B两个点,其坐标分别为,则重力加速度g=_____。

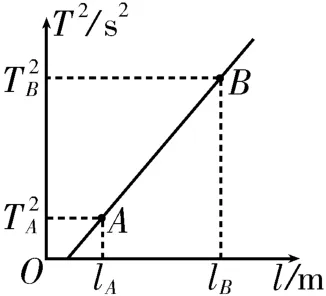
图9

参考答案：1.ABD