基于回波数据稳定性改善的雷达改善因子提升方法

钱乔龙,王 魁,陈舒敏,马振康

(1.中国船舶集团有限公司第八研究院,江苏 扬州 225101;2.解放军92692部队,广东 湛江 524067)

0 引 言

当搜索雷达执行任务时,需要在强杂波环境中检测高速运动的小目标,因此对强杂波的抑制能力就是制约搜索雷达发现小目标的重要限制因素,在现代雷达系统中,一般把对强杂波的抑制能力称为杂波改善因子。

根据资料,美军大量装备的AN/SPQ-9B低空警戒搜索雷达,具有90 dB的改善因子,在强表面杂波环境下具有很强的小目标检测能力。

1 改善因子的定义及影响因素分析

一般把杂波改善因子I定义为系统输出信杂比与输入信杂比的比值,即:

(1)

式中:Psi为输入信号功率;Pci为输入杂波功率;Pso为输出信号功率;Pco为输出杂波功率[1]。

杂波滤波器输出的杂波剩余是由多种因素引起的,一般有以下几类:

(1)外部因素:杂波特性等;

(2)雷达系统不稳定因素:雷达系统自身各种不稳定因素,如相位噪声[2]、定时抖动等;

(3)雷达接收处理系统限制因素:动目标显示器(MTI)、动目标检测器(MTD)、杂波滤波器设计性能、动态范围等。

杂波剩余功率可写为:

Pco=Pw+Px+Pj

(2)

式中:Pw为由外部因素引起的杂波剩余功率;Px为由系统不稳引起的杂波剩余功率;Pj为由接收处理限制引起的杂波剩余功率。

因此,雷达系统总的改善因子也由上述各种因素共同决定,即:

(3)

于是可推导出:

(4)

式中:Iw为只受外部因素影响时的改善因子;Ix为只受系统不稳影响时的改善因子;Ij为只受接收处理限制时的改善因子。

由上式可以看出,雷达系统总的改善因子受到3项改善因子的限制,即类似于“木桶效应”,其数值总是小于最小分项的改善因子,因此各分项改善因子常称为改善因子限制值。

2 雷达系统不稳定性影响因素分析

在3项影响改善因子的因素中,雷达系统不稳定因素主要包括信号频率稳定性、信号相位稳定性、脉冲定时抖动、脉冲宽度抖动、模数转换器(ADC)采样抖动、射频泄漏空间调制等:

(5)

式中:If为只受频率不稳影响时的改善因子;Ip为只受相位不稳影响时的改善因子;Iv为只受脉冲定时抖动时的改善因子;Ik为只受脉冲宽度抖动时的改善因子。

以脉冲定时抖动为例进行分析,定时脉冲的同步是相控阵雷达各组件单元进行发射、接收等处理的关键控制信号。作为雷达基准的脉冲,一般要求有陡峭的上升沿和下降沿,同时要求脉冲之间的时间间隔保持一致。为了减少脉冲传输过程中的损失和外部干扰,现代雷达一般使用光纤进行脉冲的传输。但是由于实际存在的噪声、光模块电路稳定性等因素影响,经过光纤传输脉冲频率或相位还是存在随机起伏,这种随机起伏就是抖动[3]。

对于相控阵雷达,如果发射触发脉冲出现这种抖动,会导致不同组件之间的发射信号产生不同的时延,对发射信号的稳定性产生影响,从而对雷达接收的回波数据稳定性产生影响。

发射定时触发脉冲抖动会对改善因子形成限制,公式如下:

(6)

式中:Δt为定时脉冲的时间抖动量;τ为发射脉冲宽度;B为发射脉冲带宽。

以现代相控阵雷达常用的光纤数字脉冲信号传输方式为例,脉冲上升沿抖动约500 ps,取τ=24 μs,Bτ=120,Δt=500 ps,则I=70 dB。

3 测试雷达系统稳定性对改善因子的影响

如上节所述,影响雷达系统稳定性的因素很多,对每种因素影响程度进行定量测量和评估,可以得到每个因素对系统改善因子的限制。然而,具体到实际的雷达设备,某些因素的测试往往较困难,但可以通过录取长时间的回波数据,对数据的稳定性进行分析,对改善因子进行计算,据此可以分析评估雷达系统总的稳定性对系统改善因子的限制。

常用的快速傅里叶变换(FFT)加窗滤波器系数和有限冲激响应(FIR)滤波器系数如图1、图2所示。

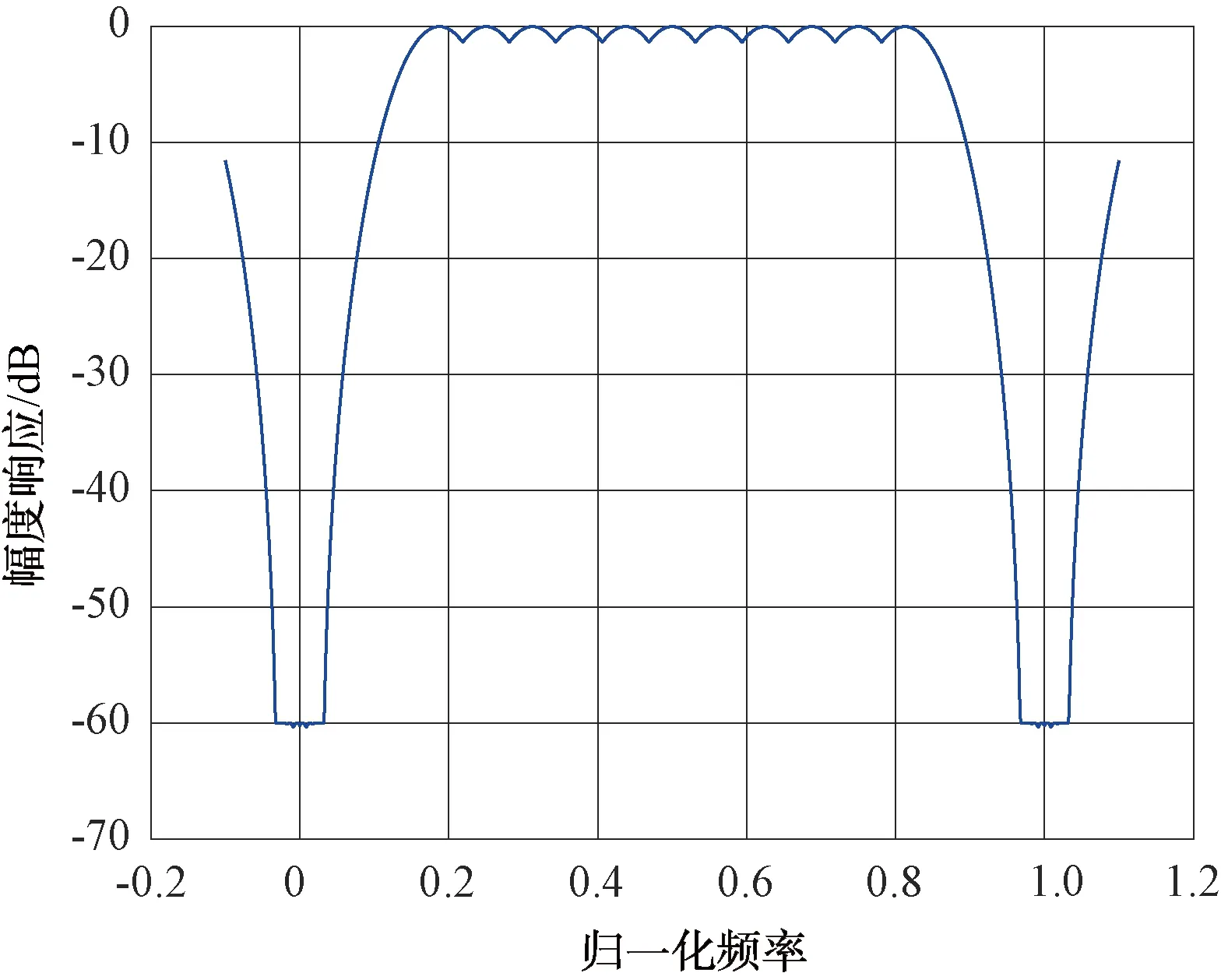
图1 FFT加窗滤波器图

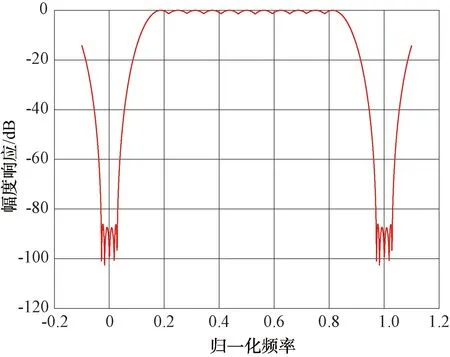
图2 FIR滤波器图

2种滤波器性能对比如图3所示。

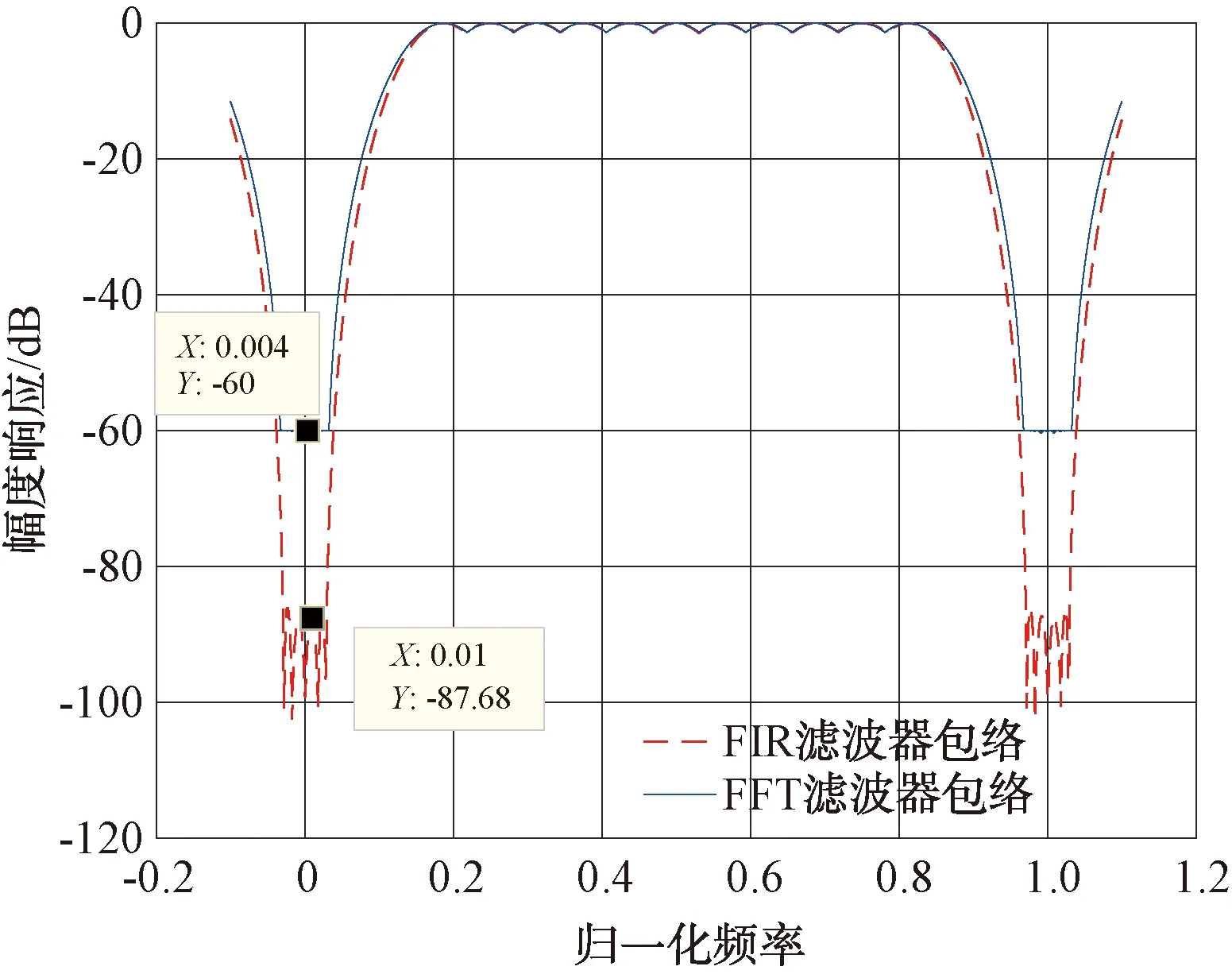
图3 2种滤波器性能对比图

选取录取的16个脉冲,进行改善因子测试,16个脉冲的幅度和相位如图4、图5所示。

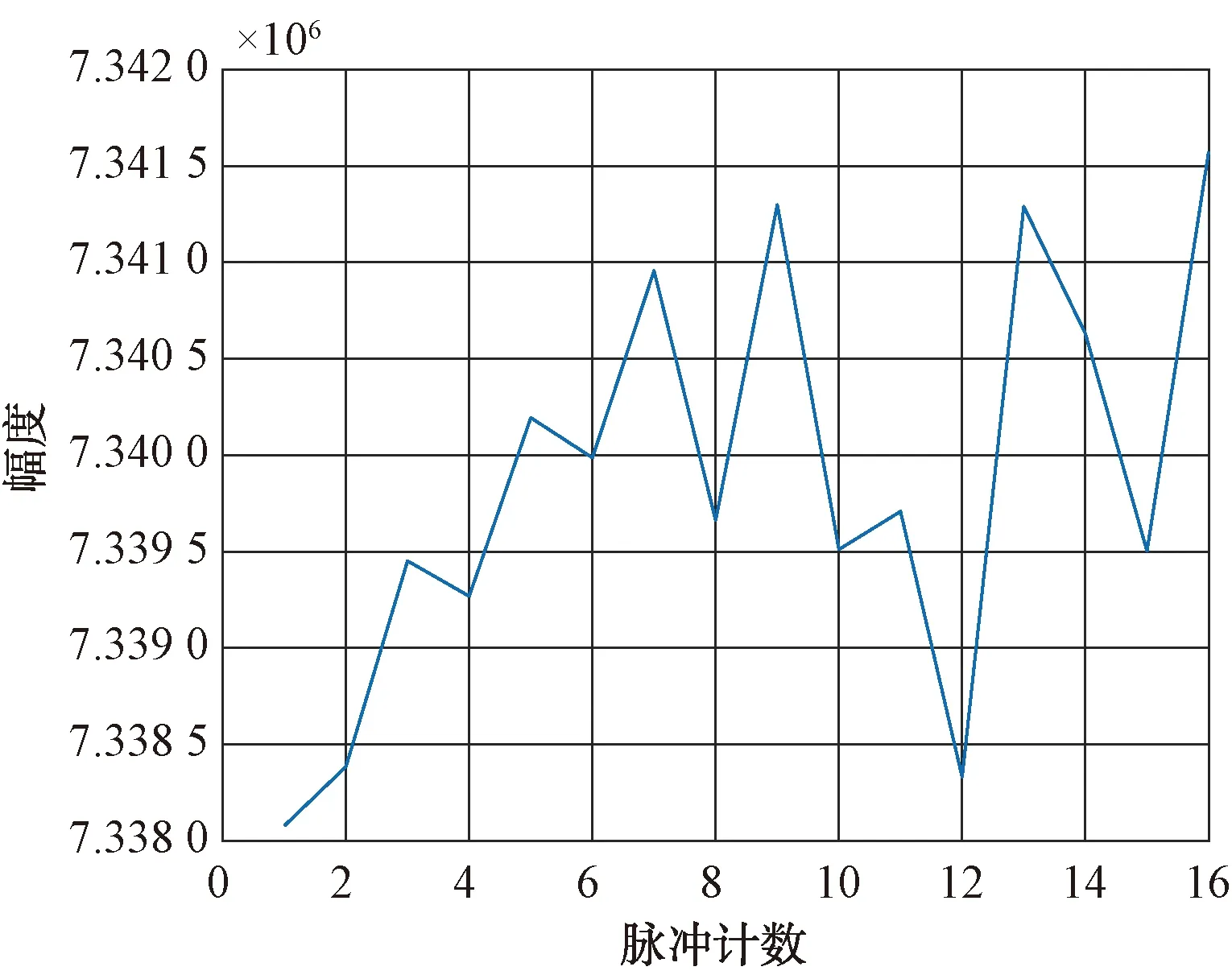
图4 16个脉冲的幅度图

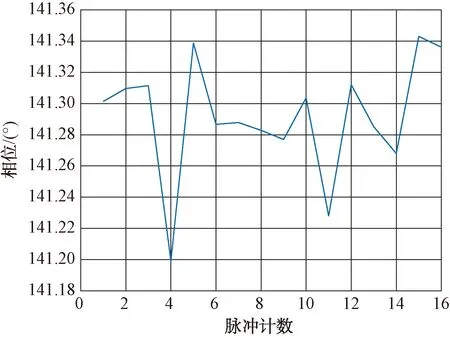
图5 16个脉冲的相位图

16个脉冲的频谱如图6所示。

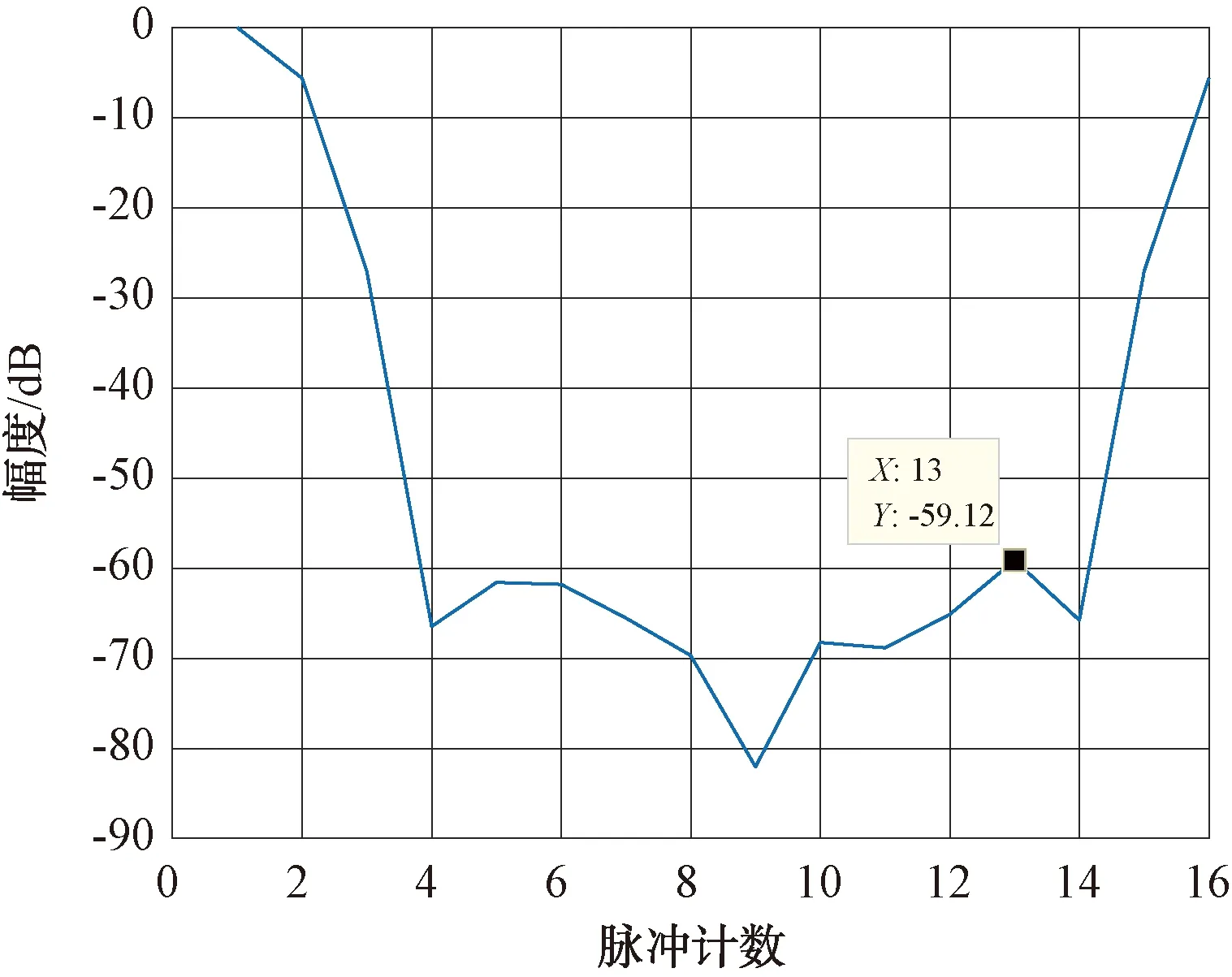
图6 16个脉冲的频谱图

FFT加窗滤波器系数处理后,改善因子为59.12 dB。

FIR滤波器系数处理后,改善因子为69.45 dB。

选取16个脉冲,只能看出短时间内的改善因子,录取长时间的数据,选取其中200个脉冲,进行改善因子均值测试,幅度抖动和相位抖动如图7、图8所示。

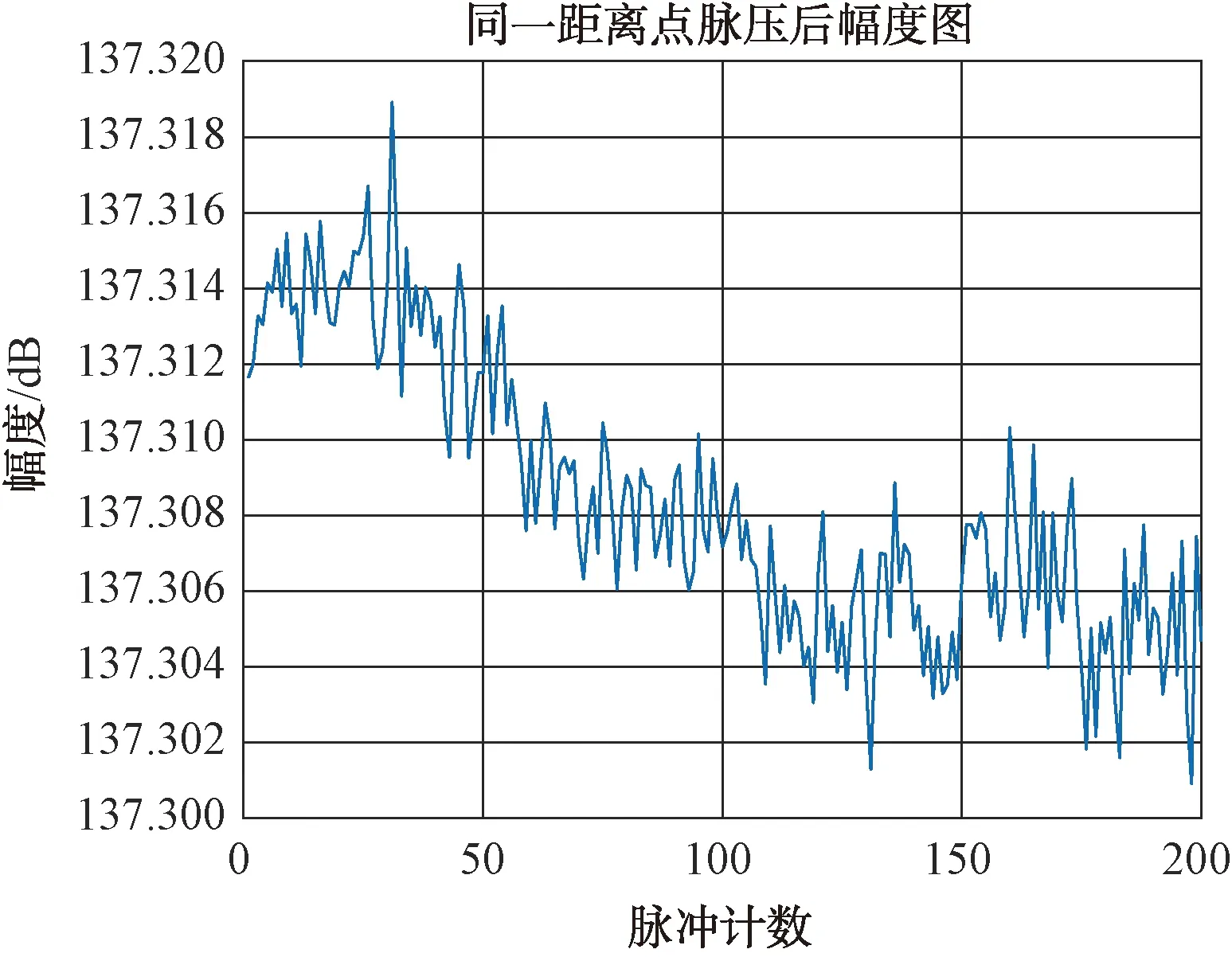
图7 200个脉冲幅度抖动图

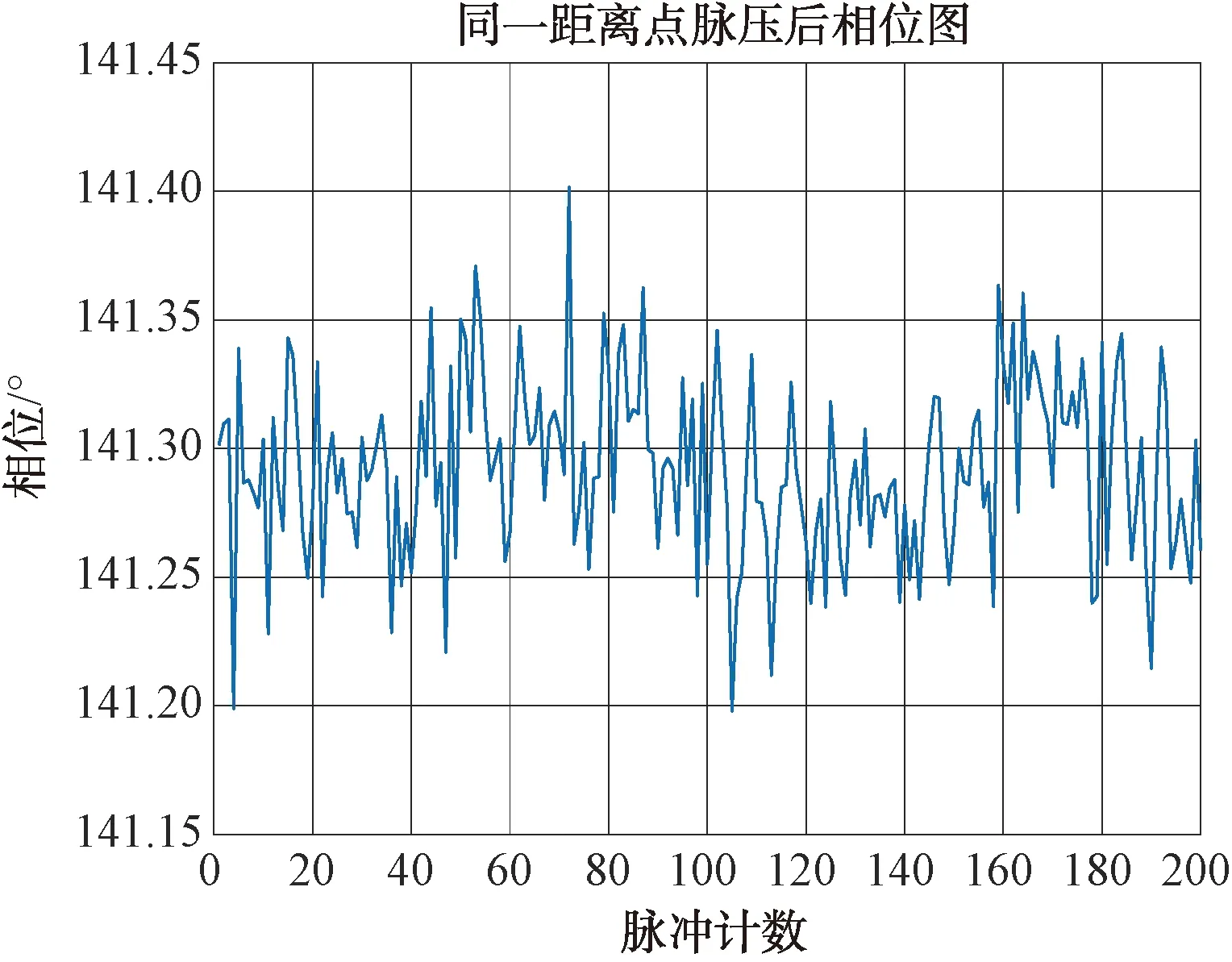
图8 200个脉冲的相位抖动图

用FFT加窗滤波器系数处理后,改善因子测试结果如图9所示。

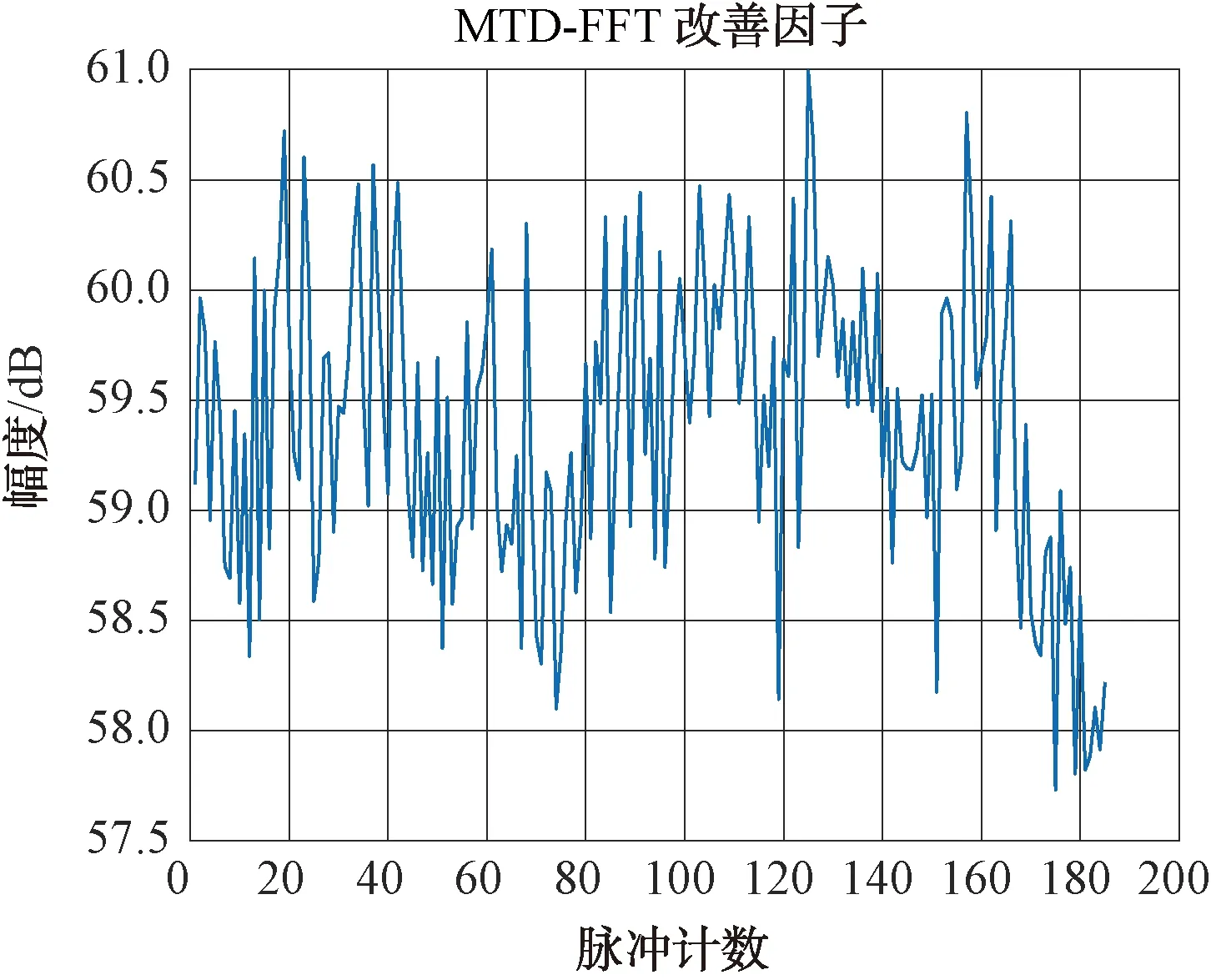
图9 200个脉冲的FFT处理改善因子图

用FFT加窗滤波器系数处理后,改善因子均值为59.5 dB,抖动范围为58～61 dB。在FFT加窗滤波器中,凹口深度只有60 dB,同时回波数据稳定性导致的影响优于60 dB,所以用FFT加窗滤波器处理,限制改善因子的主要因素是滤波器凹口深度,而不是系统稳定性。

用FIR滤波器系数处理后,改善因子测试结果如图10所示。

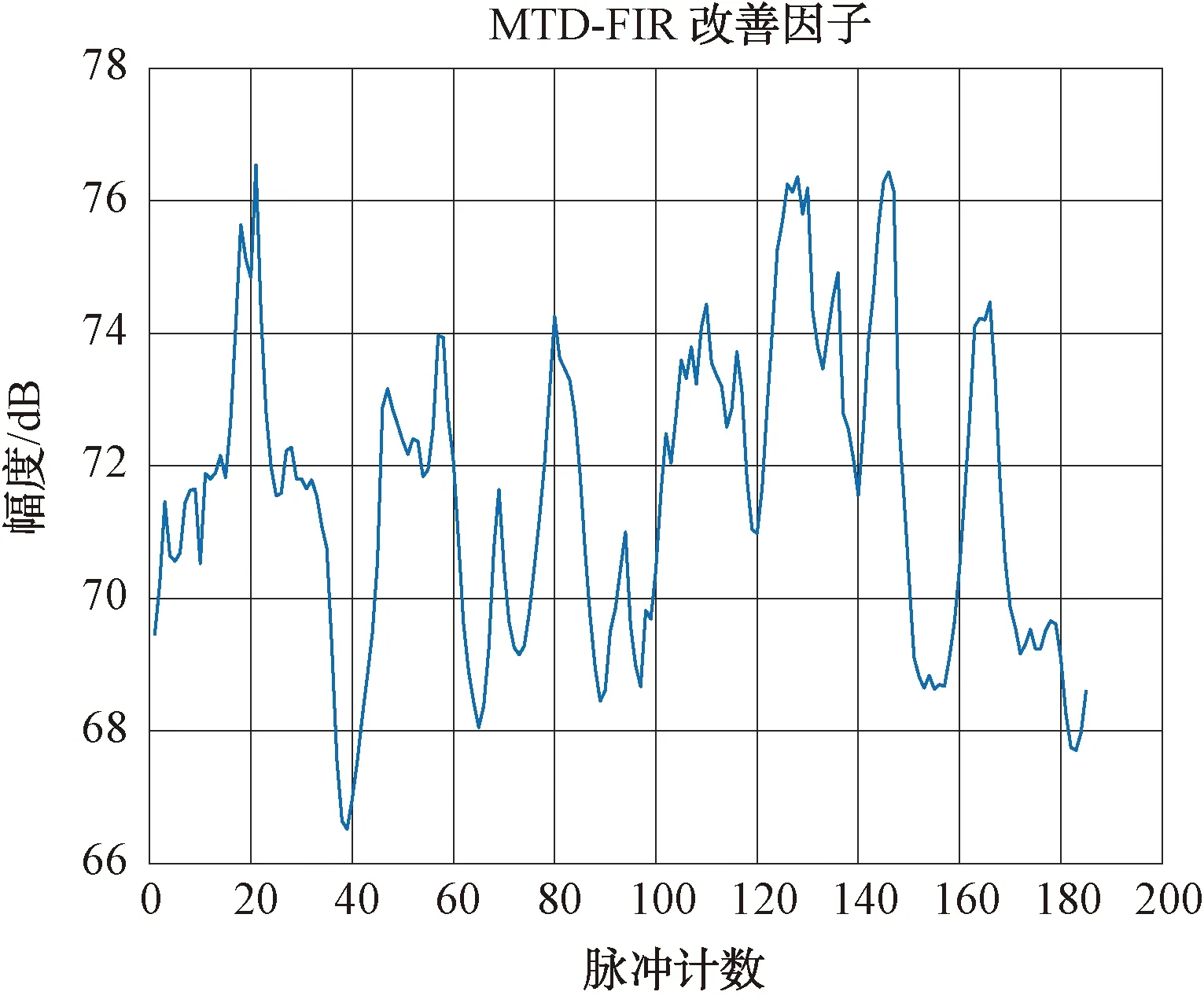
图10 200个脉冲的FIR处理改善因子图

用FIR滤波器系数处理后,改善因子均值为72 dB,抖动范围为66～76 dB。在FIR滤波器中,凹口深度达到87～100 dB,但是在用FIR滤波器系数处理后,改善因子并未达到滤波器的性能,且录取的数据动态范围足够,此时,限制改善因子的主要因素就是回波数据的稳定性。

根据上文对雷达系统的稳定性影响因素分析,提高雷达系统的稳定性主要通过提升雷达相控阵面的硬件稳定性指标和噪声系数进行,但是在工程实现中,这一类指标的提升所带来的硬件成本的提升相对较大,且提升的困难较大。以脉冲定时抖动为例,通过选用小抖动的光模块、选用高稳定性的时钟源等方法,可以将光传输的定时脉冲抖动由500 ps提高到220 ps,但同时也带来成本的上升。

针对这一情况,本文提出一种在脉压后改善回波数据稳定性的方法来提升雷达改善因子。

4 平滑处理算法及应用仿真分析

4.1 算法原理

平滑滤波算法是常用的低频增强的滤波技术,主要目的是用来消除噪音和模糊处理。Saviteky-Golay是一种数字平滑滤波器,通过不加权的线性最小二乘法与一个低阶多项式拟合,在时域内直接对数据进行平滑,以达到平滑噪声数据的目的,这样既能够提高数据的精度,又能保持信号的宽度和趋势。

设1组雷达回波数据为xk,k=1,2,…,N,共N个数据,取窗口内数据xk-w,…xk,…,xk+w进行平滑滤波处理。根据Saviteky-Golay平滑公式,有:

(7)

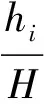
4.2 应用仿真

对脉压后的16个脉冲用Saviteky-Golay数字平滑滤波器进行平滑处理,平滑处理后幅度和相位如图11、图12所示。

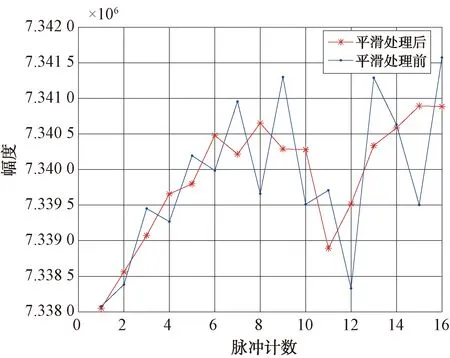
图11 16个脉冲平滑处理前后幅度对比图

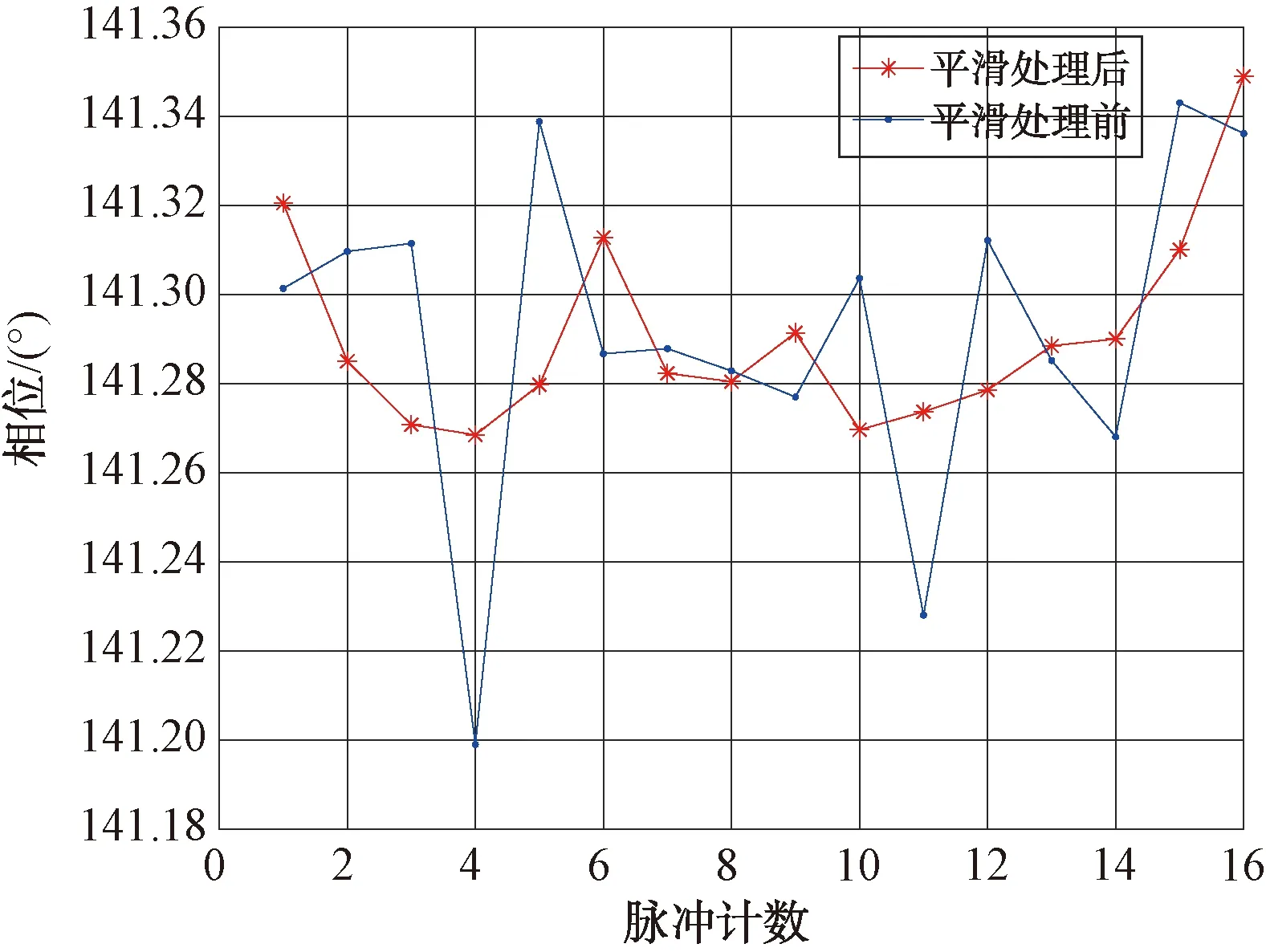
图12 16个脉冲平滑处理前后相位对比图

平滑处理后,16个脉冲的频谱如图13所示。

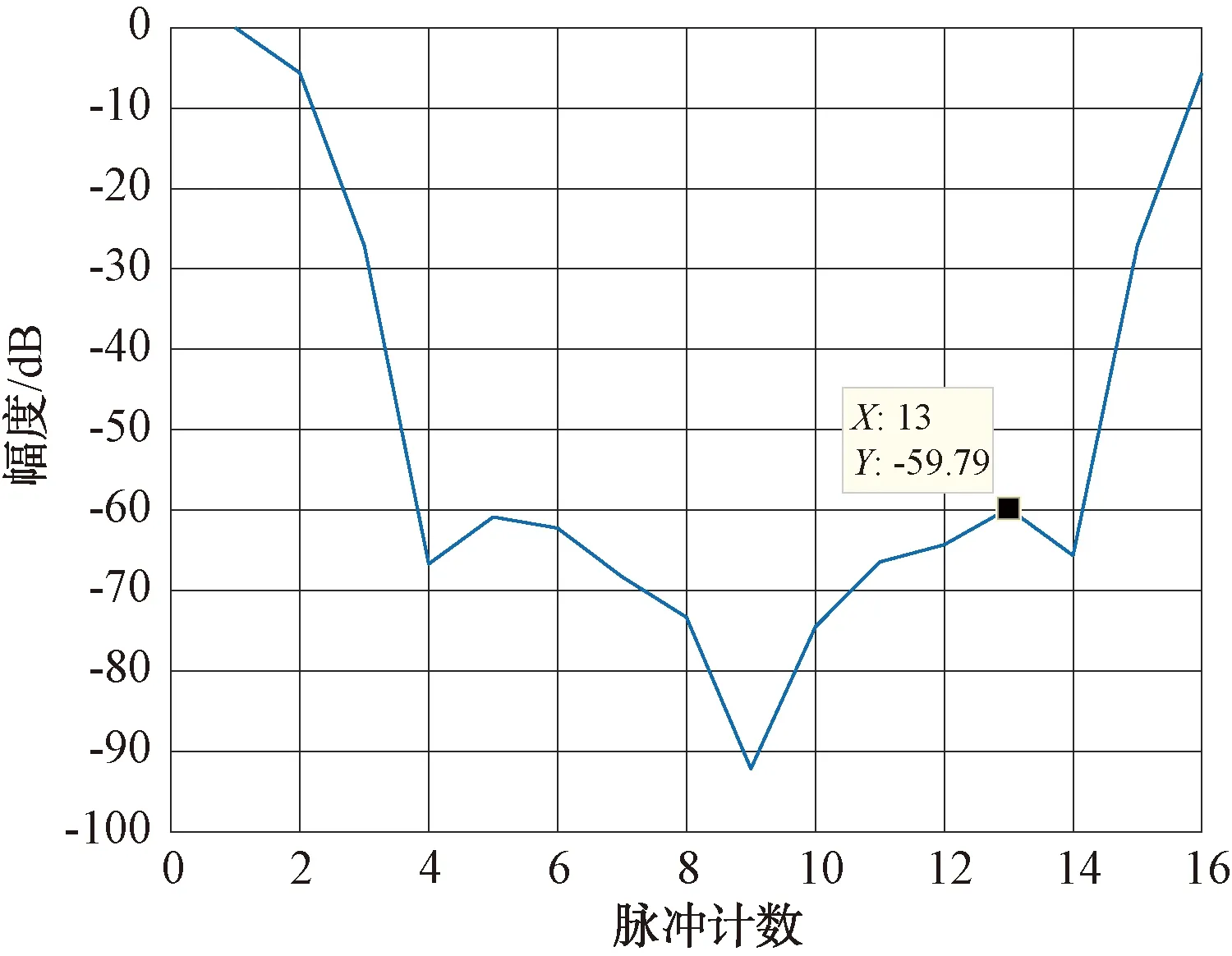
图13 16个脉冲平滑处理后频谱图

用FIR滤波器系数处理后,改善因子为80 dB,相比平滑处理前,改善因子提升20.88 dB。

对16个脉冲平滑前后的方差和平滑引起的均方根误差进行计算,评估平滑对数据的影响,平滑处理引起的幅度和相位的一次差如图14、图15所示。

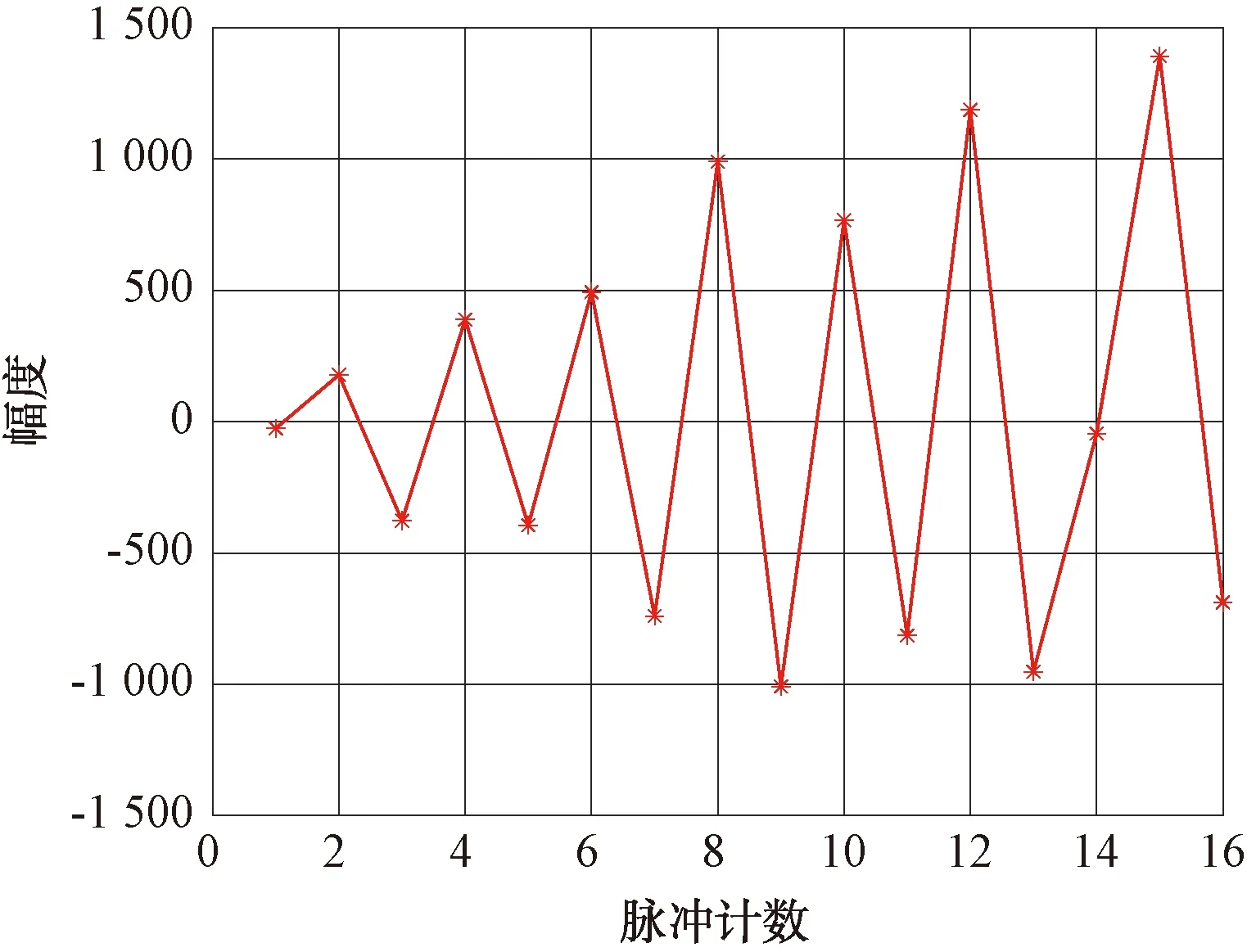
图14 16个脉冲平滑处理引起的幅度一次差图

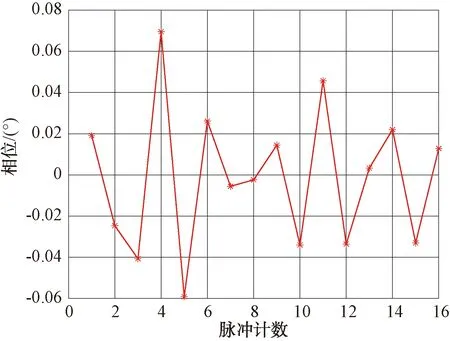
图15 16个脉冲平滑处理引起的相位一次差图

由图14、图15可见,原始数据幅度方差为1 093 870.72;平滑处理数据幅度方差为689 339.95;原始数据相位方差为0.001 4;平滑处理数据相位方差为0.000 45;平滑处理引起的幅度偏差均方根为760.50;平滑处理引起的相位偏差均方根为0.033°。

可以看出,平滑处理后,回波数据的幅度和相位方差减小,且偏离数据的均方根误差适中。

对200个脉冲按照16个脉冲滑动进行平滑处理,改善因子如图16所示。

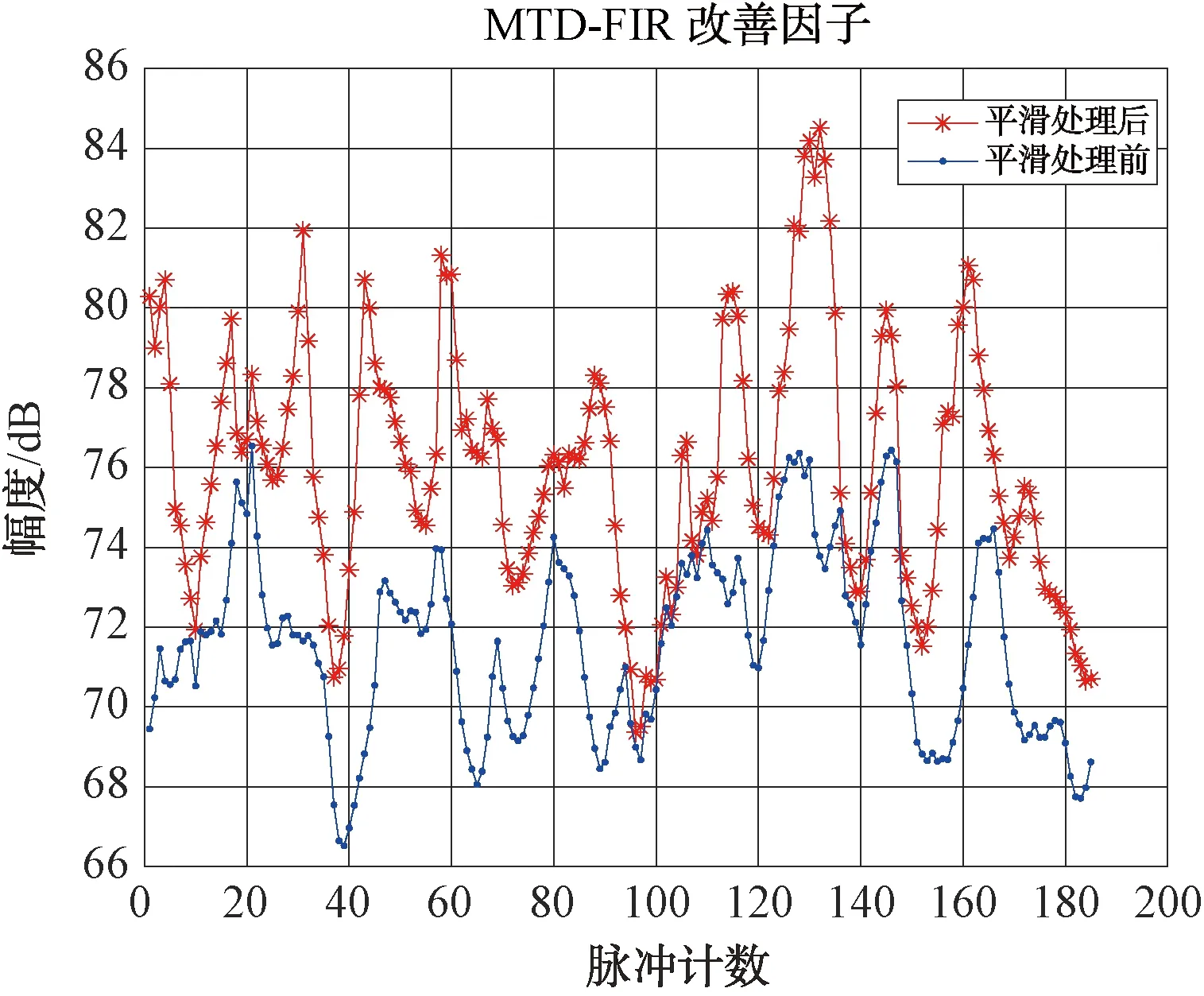
图16 200个脉冲平滑处理前后改善因子对比图

从图16可以看出,平滑处理后,改善因子均值为76 dB,抖动范围为70～84 dB。相较于平滑前,改善因子有提升,但是改善因子的抖动还是较大。因此,进一步使用曲线拟合进行改善分析。

5 曲线拟合处理算法及应用仿真分析

5.1 算法原理

曲线拟合算法,一般可以使用多项式进行曲线拟合,可限定最佳拟合为在数据点的误差平方和尽可能小,这在数学上被称为多项式的最小二乘曲线拟合。

假设采用3阶多项式进行曲线拟合,1组雷达回波数据为xk,k=1,2,…,N,共N个数据。曲线拟合公式如下:

(8)

式中:a、b、c为待定的多项式系数,找到1组系数,使得yk与xk误差的平方和w尽可能小:

(9)

5.2 应用仿真

对脉压后的16个脉冲用3阶多项式进行最小二乘曲线拟合处理,处理后幅度和相位如图17、图18所示。

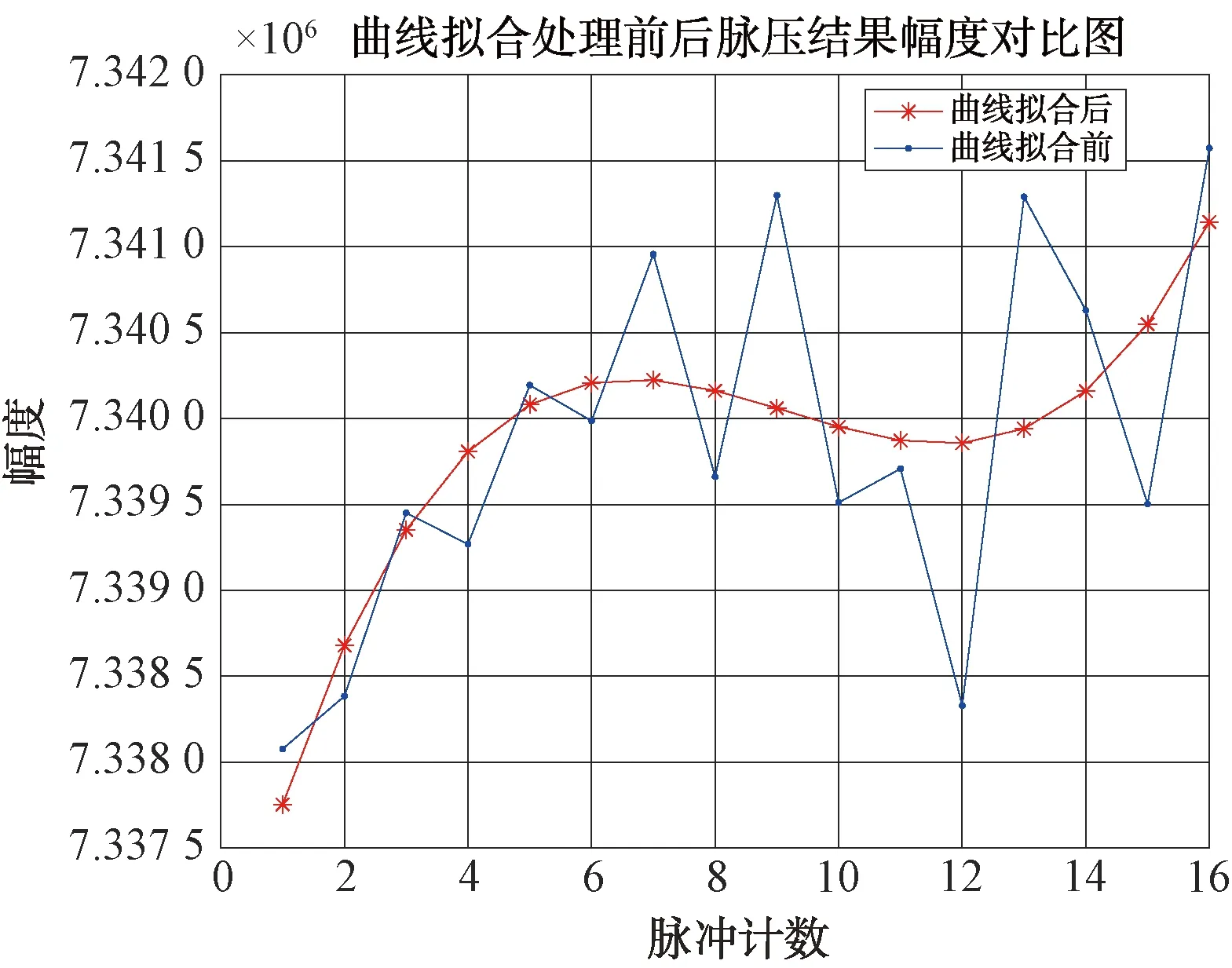
图17 16个脉冲拟合处理前后幅度对比图

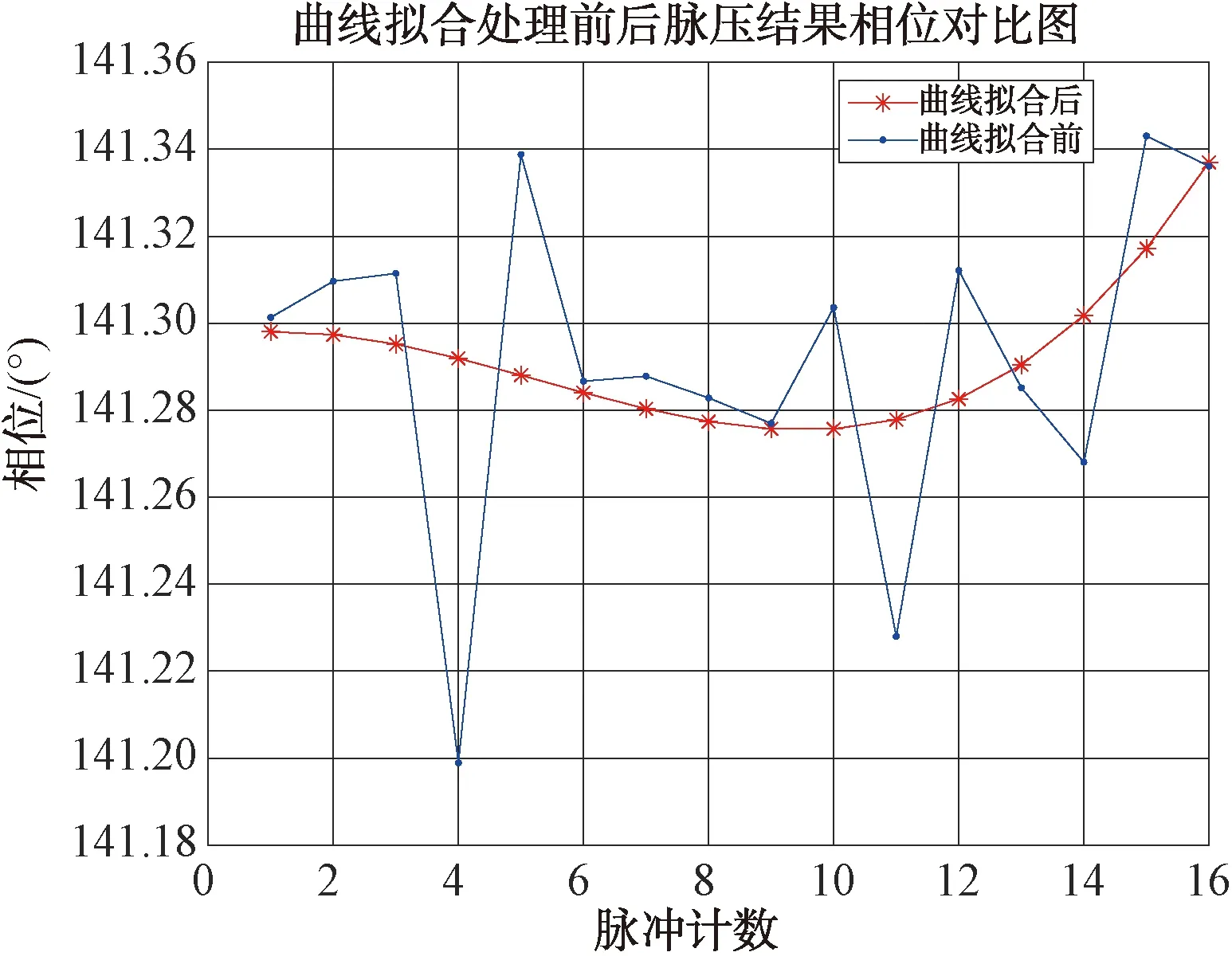
图18 16个脉冲拟合处理前后相位对比图

拟合处理后,16个脉冲的频谱如图19所示。

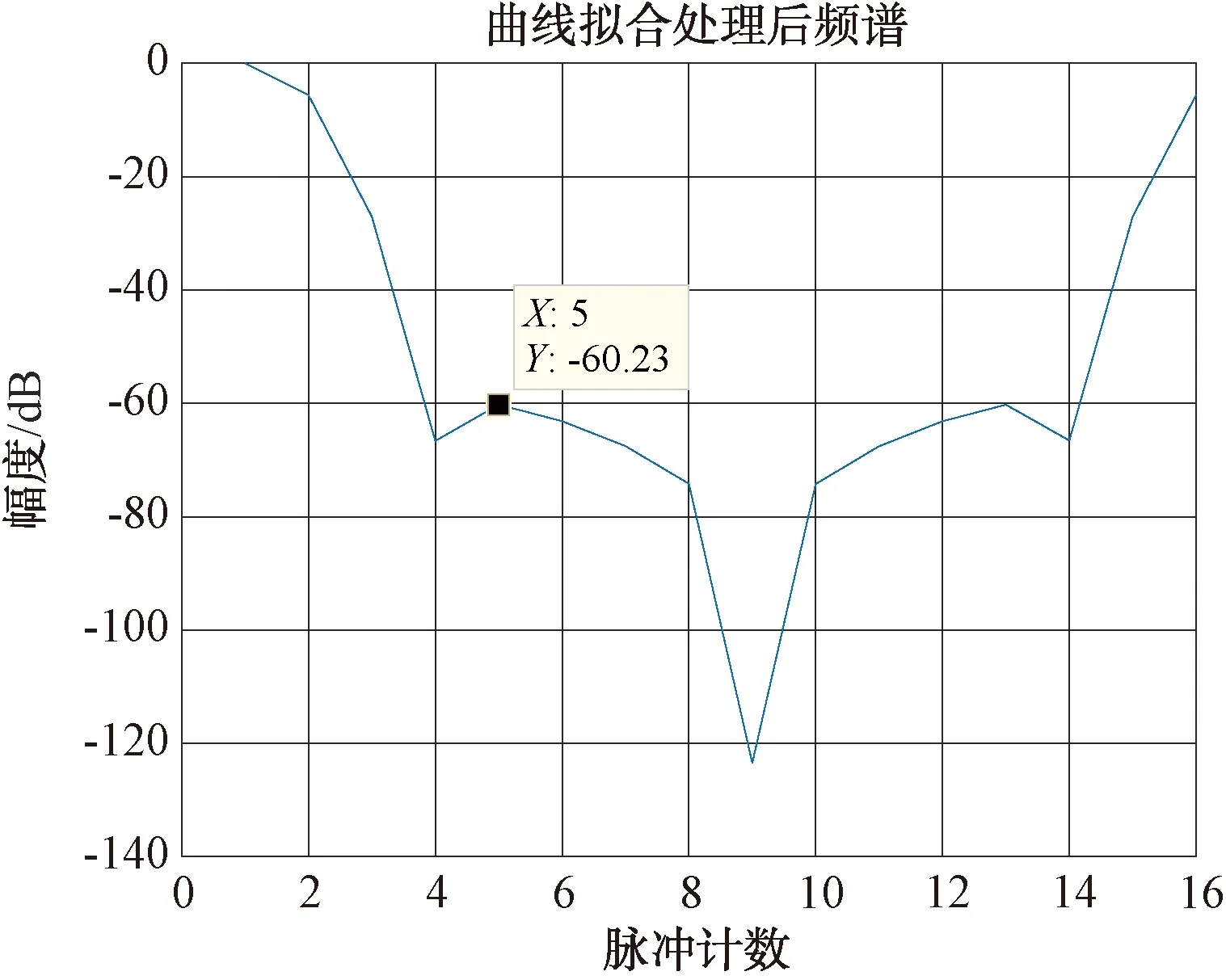
图19 16个脉冲拟合处理后频谱图

用FIR滤波器系数处理后,改善因子为98 dB,相比曲线拟合处理前,改善因子有效提升。

对16个脉冲拟合处理前后的方差和拟合处理引起的均方根误差进行计算,评估拟合处理对数据的影响,拟合处理引起的幅度和相位的一次差如图20、图21所示。

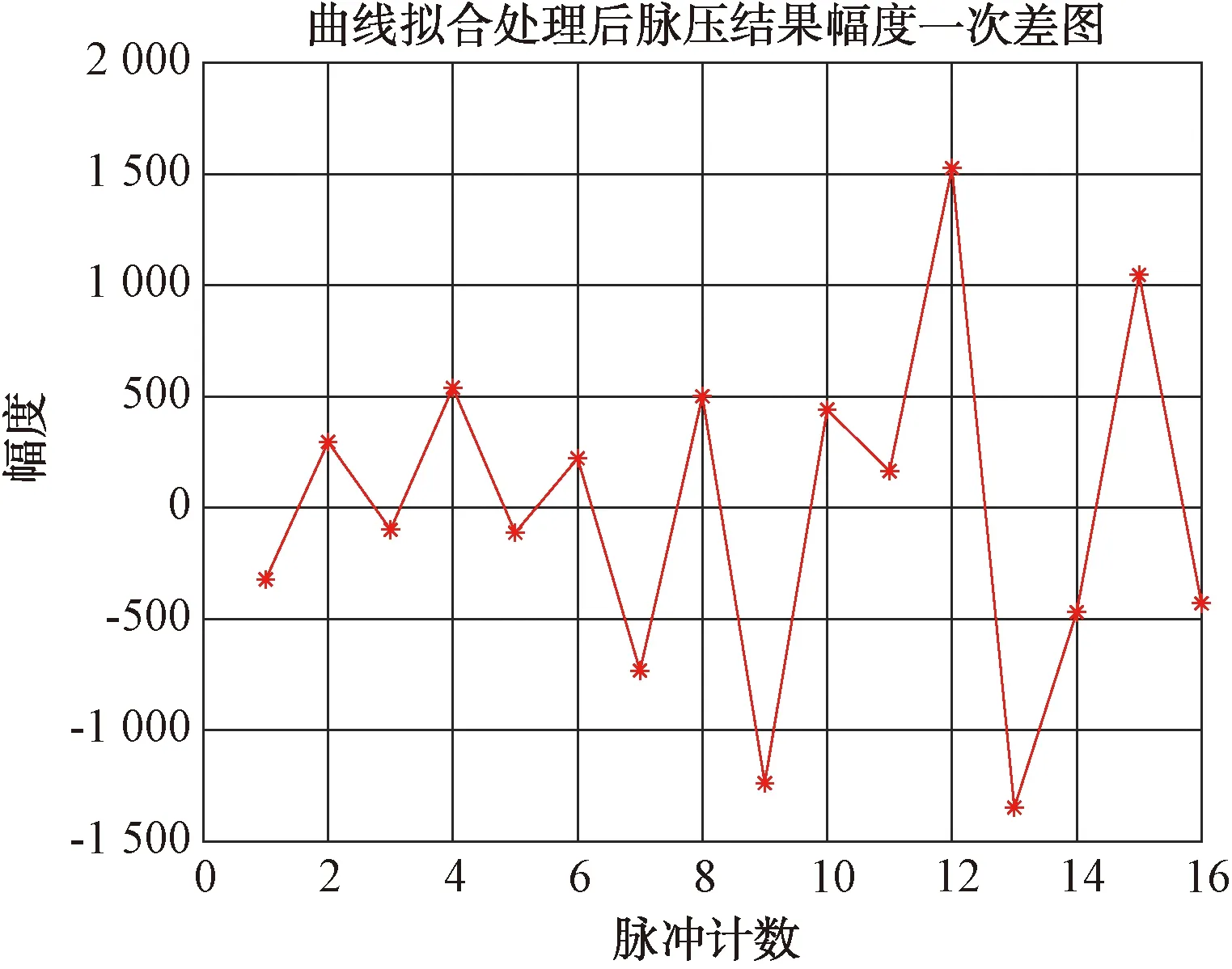
图20 16个脉冲拟合处理引起的幅度一次差图

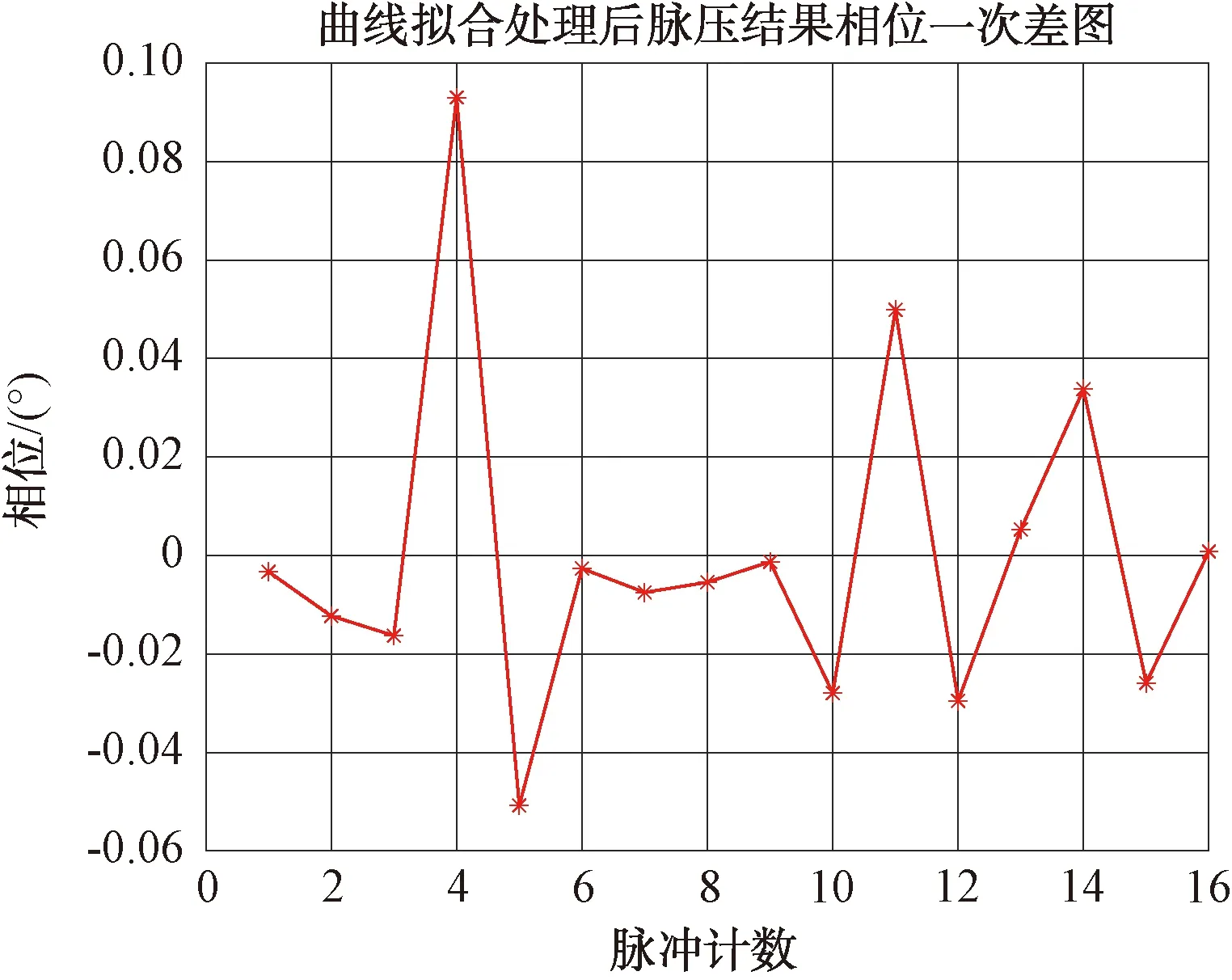
图21 16个脉冲拟合处理引起的相位一次差图

由图20、图21可见,原始数据幅度方差为1 093 870.72;拟合数据幅度方差为546 839.36;原始数据相位方差为0.001 4;拟合数据相位方差为0.000 25;曲线拟合处理引起的幅度偏差均方根为739.52;曲线拟合处理引起的相位偏差均方根为0.033°。

可以看出,拟合处理后,回波数据的幅度和相位方差相比平滑处理进一步减小,所以改善因子进一步提升。

对200个脉冲按照16个脉冲滑动进行曲线拟合处理,改善因子如图22所示。

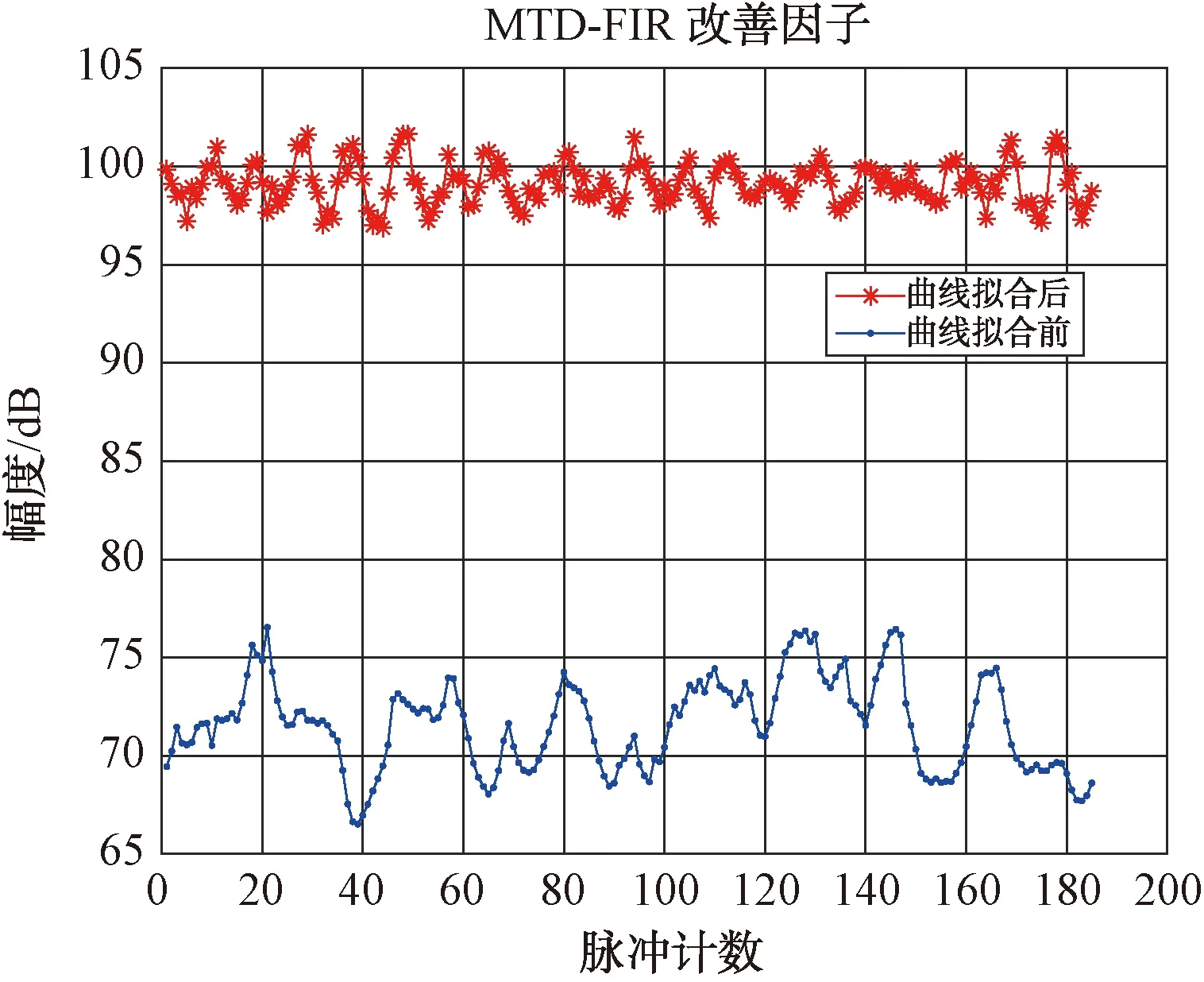
图22 200个脉冲曲线拟合前后改善因子对比图

从图22可以看出,拟合处理后,改善因子均值为98 dB,抖动范围为96～102 dB。相比于平滑处理,曲线拟合处理后改善因子进一步提高,且不同组脉冲的改善因子抖动显著减小,更趋于稳定。

曲线拟合算法可以与常规雷达信号处理算法结合,在脉压完成后,动目标处理之前,对16个积累脉冲的幅相数据进行曲线拟合,平滑幅度和相位的抖动。曲线拟合前,FIR动目标处理改善因子为69.45 dB。曲线拟合后,FIR动目标处理改善因子为98 dB,曲线拟合算法对改善因子的提高贡献了28.55 dB,信号处理算法流程图如图23所示。

图23 信号处理算法流程图

6 结束语

本文首先对雷达系统改善因子及其影响因素进行分析,重点分析并测试了雷达系统稳定性对改善因子的影响,在雷达系统硬件稳定性提升代价较大的情况下,通过在脉压后,从数字端对回波数据进行平滑处理和曲线拟合处理2种不同的方式提升雷达改善因子,并对比分析了2种方法的性能差异。在固定阵下,曲线拟合处理可以明显改善回波数据的稳定性,显著提升改善因子至98 dB,达到滤波器系数的限制瓶颈。