在图形转换中建立特征关联

屈婷

“长方体的认识”是人教版数学五年级下册第三单元的内容。本课旨在引导学生经历观察、操作、想象等活动，探索并发现长方体的特征及各组成元素之间的关系，培养学生的空间观念和推理能力。

一、借助实物观察，提取直观特征

教学中，教师可引导学生迁移平面图形的认识经验，通过有目的、有重点的观察，形成对长方体特征的基本认识。

笔者先出示生活中的长方体物品，接着用课件出示一个长方形，并提问：“与长方形相比，长方体有什么不同？在学习长方形时，我们是从哪些方面进行研究的？”学生回答：“长方形是平面图形，长方体是立体图形。研究平面图形时，我们一般从顶点、角、边三方面进行研究。”笔者设疑：“如果要研究长方体，你认为可以从哪些方面研究？与研究平面图形相比有什么不同？”通过交流，学生一致认为：认识立体图形，除了从点、角、边（棱）三个角度研究，还要研究面的特点。然后，笔者引导学生以小组为单位观察手中的长方体模型，研究长方体各组成元素的数量及位置特点，并组织学生交流。一名学生回答：“长方体有8个顶点、24个直角、12条棱、6个长方形的面。”笔者向学生介绍长方体的顶点、棱、面，并追问：“怎样数出面的数量？”有的学生按相对的面有几组去数，有的学生按方向数（先数侧面的四个面，再数上下两个面）。笔者追问：“怎样数棱？”学生回答：“上下两个面各有4条棱，侧面也有4条棱，共12条棱。”

以上教学，笔者引导学生认识了长方体组成元素的数量特征，通过有序地数初步感知面和棱的位置特征。

二、借助操作体验，获取关键特征

长方体的面和棱还有“大小”或“长短”的特征。教学中，教师可将三维的体拆解为二维的面和一维的棱进行探索。鉴于此，笔者设计了两个操作活动。

活动一：借体画面，体会长方体面的特点

笔者引导学生思考长方体的6个面在大小上有什么关系，让学生借助长方体模型，将长方体的面画在方格纸上进行研究。学生完成后，笔者展示画了6个完整面的学生作品，并提问：怎么判断这些面就是长方体模型的面？学生回答：可以用剪刀把画在方格纸上的面剪下来，放到长方体模型上还原，也可以量出长方体上长方形面的长和宽，与画下来的面作比较。笔者继续问：这些画下来的面在大小上有什么特点？学生回答：长方体的6个面可以分成3组，每组的两个面完全相同。笔者追问：这些完全相同的面分布在长方体的什么位置？有的学生通过将画下来的面剪下来，先重合、再还原到长方体模型上进行验证；还有的学生借助画下来的长方形的长和宽所占的格子数来证明。随后，笔者出示两幅画了3个面的作品（图略），并提问：“2号作品和3号作品只画了3个面，是来不及画其他的面吗？这样可以探究出长方体相对的面完全相同的特征吗？”通过讨论，学生发现：2号作品虽然只画了3个面，但这3个面可以代表三组面，把它们剪下来与模型上的面比对，也能发现长方体3组相对的面完全相同；3号作品的3个面中，有两个面完全相同，只能发现长方体有两组面完全相同。

活动二：借体画棱，体会长方体棱的特点

笔者提问：长方体有12条棱，你认为描出几条棱就能研究出长方体棱的特点？学生认为：长方体的面可以分为3组，6个面只用画3个，那么12条棱可能画6条就可以了。还有学生认为，可以不用画，前面画的面上就有棱，直接在面上描出棱再研究就可以。笔者让学生用自己的方法描出长方体的棱，研究12条棱在长短上有什么特点，并谈谈自己的发现。第一名学生在长方体的上面、左面、前面上分别描出2条不同的棱，通过数格子，发现这6条棱的长度只有3种，发现长方体相对的棱长度相等。第二名学生通过转动长方体模型，发现每条棱都能转到侧面，侧面的4条棱都相等，认为只用描3条棱就可以了。第三名学生通过观察方格纸上描下来的3个不同的面，发现棱的长度只有3种，3厘米、4厘米、5厘米的棱各有两条，再乘2就是12条，说明长方体的12条棱可以分为3组。笔者肯定了3名学生的操作，并提问：这里有一些长度分别为3厘米、4厘米、5厘米的纸条，你知道它们分别是长方体的哪些棱吗？学生在给长方体找棱的过程中，发现长方体中互相平行的棱长度相等。笔者顺势总结：这3组棱分别叫做长方体的长、宽、高。

三、借助想象推理，建立特征关联

在体的构成中，面和线、面和面的联结与架构至关重要。教师要借助直观操作，引导学生发挥想象力，通过平面图形与立体图形之间的转换，感知长方体的结构。

课堂上，笔者引导学生进行如下交流。

师：有若干张长方形硬纸板，它们的大小分别为：①5×3；②4×3；③4×5；④5×5；⑤4×4；⑥3×3。以①号长方形纸板为正面，哪些长方形能与它拼成一个长方体？哪些不能？为什么？

生：⑤号长方形不行，它與①号长方形没有相等的边。

生：②号长方形可以拼在①号长方形的左边，也可以拼在①号长方形的右边。⑥号长方形也可以。

生：③号长方形和④号长方形可以拼在①号长方形的上面或下面。

师：为什么这些图形能和①号长方形拼成一个长方体？它们之间有什么联系？

生：①号长方形长5厘米、宽3厘米，只要一个长方形有一条边是5厘米或3厘米，就能与①号长方形拼接成功。

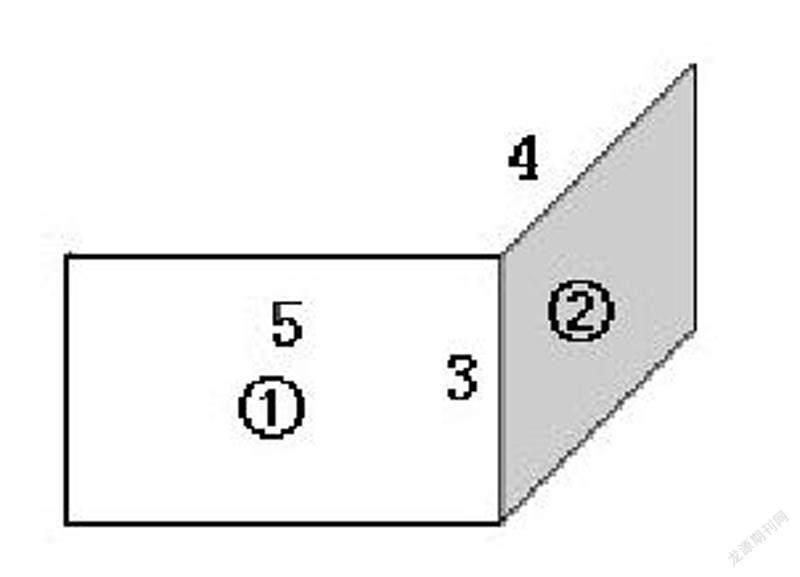
师：如下图，如果选择将②号长方形拼在①号长方形的右边，拼接之后的图形还有几条边？

生：有7条边，这两条拼在一起的边合成了一条，变成了长方体的棱。

师：这时可以选择哪些面作为上下面进行拼接？

生：③号长方形和④号长方形都可以，因为它们都有一条边是5厘米。

生：只能选③号长方形，④号长方形可以和①号长方形拼，不能和②号长方形拼。

师：为什么第三个面不能随便选？长方体至少确定几个面，就能确定长方体的形状？

生：两个面就能确定。选定两个相邻的面后，长方体的长、宽、高就不能变了。

师（撕下两个面，露出棱）：至少用几条棱可以确定长方体的形状？

生：长、宽、高各留下一条，即三条棱就可以。

师：如果选择将⑥号长方形拼在①号长方形的右边，接下来可以怎么选？

生：只能选①号长方形，长方体中有一个面是正方形时，其他4个面完全相同。

师：长方体有6个面，每个面有4条边、4个顶点，一共有24条边、24个顶点，为什么长方体只有12条棱、8个顶点？

生：每两个长方形的面拼在一起时，就有两条边合成一条棱，所以有“24÷2=12（条）”棱。长方体的顶点是3个面连在一起的地方，每3个面合成一个顶点，所以有“24÷3=8（个）”顶点。

在操作与观察活动中，学生不仅体会到长方体的面与棱在空间位置上的特点，而且对长方体的构成元素之间的关联有了更深层次的理解。

（作者单位：宜城市窑湾小学）

责任编辑  张敏