面向航空结构低频振动的力电耦合超材料板设计

沈显邦，易凯军，*，景旭贞，刘智元，朱睿

1．北京理工大学 宇航学院，北京 100081

2．中国空间技术研究院 总体设计部，北京 100098

振动会对飞机产生诸多负面影响，如使结构出现疲劳与损伤、产生噪声影响乘机环境、干扰机载敏感设备工作等，特定情况下甚至可能导致飞机解体，因此振动控制对飞机的安全性、舒适性等都至关重要。

机身结构的振动主要来源于发动机的振动以及外部流动引起的振动等。由于机身以薄壁板壳结构为主，而弯曲波是板结构中最容易被激发的波，也是最重要的能量携带波，振动主要以弯曲波的形式在机身结构中传递。因此，控制结构中的弯曲波传播是抑制机身振动的有效手段。结构中波动传输控制的常规方法是在结构表面敷设阻尼材料吸收弹性波。然而，受飞机附加质量和空间约束限制，阻尼材料对低频弹性波的抑制效果有限，弹性波的低频振动控制仍缺少有效手段。

21 世纪初提出的声波/弹性波超材料为低频弹性波控制提供了新思路。声波/弹性波超材料最先由中国香港学者提出［1］，其利用局域共振效应，在低频范围实现负的等效参数产生禁带，阻隔弹性波传播，因此被广泛探索用于梁、板、壳等工程结构的减振设计［2-4］。然而，超材料在工程中用于低频减振依然存在一些难以克服的问题。首先，超材料实现低频禁带需要引入较大额外质量，并且引入的质量随着频率的降低而增加，虽然缩减附加在结构上的谐振子个数可减少附加质量，但禁带阻隔弹性波完全消除共振的效果可能减弱（甚至消失），仅能利用谐振子的阻尼效应降低共振幅值［5-6］。其次，由于强频散特性，局域谐振产生的带隙狭窄，无法实现宽频的减振效果。另外，基于机械谐振子的被动超材料设计加工完后，禁带位置很难再更改，无法根据装备所处的工况和环境做出自适应的调整。这些缺点严重限制了被动超材料在工程中的应用。针对禁带窄的问题，研究者提出了一些解决方案，如设计含黏弹阻尼材料的多频共振单元［7-8］，或者利用惯性放大机构增加质量的惯性效应［9］。然而，多频共振单元会进一步增加系统的质量和体积；惯性放大机构复杂，实际使用受限。

近年来，基于压电材料和分流电路的力电耦合超材料受到越来越多的关注。力电耦合超材料能够利用外部分流电路来调节等效材料参数，从而可以在不破坏弹性结构完整性、不增加过多额外质量的前提下实现对波动的调控，因此具有突破前文所述被动超材料不足的潜力。Thorp 等［10］最先利用谐振电路分流的压电阵列设计了力电耦合超材料梁。其基本元胞由基底梁结构、压电片以及谐振分流电路组成。研究表明，谐振电路通过压电材料的力电耦合效应作用在超材料梁上，在宏观上实现了禁带的效果。通过调节电路的参数即可实现对禁带位置甚至作用范围的调控。与机械局域共振引起的禁带类似，谐振电路导致的禁带同样可以出现在亚波长范围，因此谐振分流力电耦合超材料可用于低频振动噪声抑制［11-14］。虽然，谐振分流力电耦合超材料的禁带在较大频率范围内可调，然而其禁带依然狭窄，单次只能抑制一阶振动模态，工程中很多情况下结构多个模态会被激发，需要同时能抑制多个振动模态的方法。因此，如何拓宽低频禁带成为力电耦合超材料研究中的关键问题之一。Fan 等［15］利用负电容电路来拓宽禁带范围，结果表明有效。Wang 等［16］通过增强电路谐振效果，一定程度上扩大了禁带的作用范围，提高了禁带内的波衰减效果。Li L 等［17］将连接不同压电作动器的电路通过一定方式互联，在低频得到了耦合禁带。Li X P 等［18］利用反馈控制策略来自适应调节机械振子的刚度，获得了更宽的低频禁带。Yi等［19］利用数字电路编程使得超材料梁不同单元中的电路谐振频率在空间上成梯度变化实现较宽频的禁带效果。Wang［20］、Sugino［21］和Yi［22］等同样利用数字电路和精细设计的控制传函，在超材料结构中获得了多重禁带效果，达到拓宽禁带有效范围的目的。此外，Yi等［23］将负电容与电感谐振电路组合，有效拓宽了超材料梁中的低频禁带。

本文将负电容和电感谐振电路组合用于拓宽力电耦合超材料板结构中的低频禁带，实现低频宽带的振动抑制效果。通过理论分析获得力电耦合超材料板等效抗弯刚度的解析表达式，在此基础上揭示负电容拓宽超材料板禁带的机制、研究负电容对禁带范围的调控规律，最后数值验证力电耦合超材料板的低频宽带减振效果。

1 力电耦合超材料板设计

1.1 力电耦合超材料板模型

图1 为力电耦合超材料板及其单元的示意图，每个单元由基底板、粘贴在板结构上下表面由压电陶瓷制成的压电片（PZT）及跟压电片相连的分流电路组成，分流电路的阻抗用Zsu表示。压电片极化方向与z轴同向，压电片与板粘接的表面电极接地。单元中，上下压电片及其覆盖的基底板形成的三明治结构部分用A表示，其余部分用B表示。lp、lb、hp、hb分别为基底板和压电片的宽度和厚度。

图1 力电耦合超材料板及其单元示意图Fig.1 Sketch of electromechanical coupled metamaterial plate and its unit

将负电容与电感组合用于拓宽低频禁带。负电容C0和电感L元件可以串联或者并联，如图2 所示，其中，PZT 用一个电流源和常应变下的固有电容Csp并联等效表示。两种分流电路对应的阻抗Zsu如表1 所示，同时，表1 中也给出了纯电感分流电路的阻抗，其中j为虚数单位；ω为角频率。

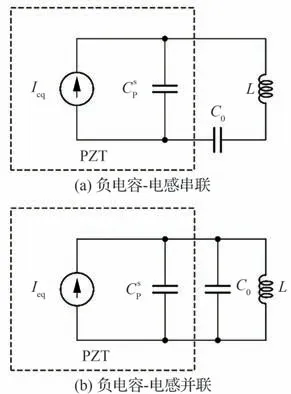
图2 两种分流电路配置Fig.2 Two shunts configurations

表1 不同分流电路的阻抗Table 1 Impedance of different shunts

1.2 等效抗弯刚度

力电耦合超材料板的等效抗弯刚度主要通过3 步获得。首先，获得连接分流电路的压电片的等效拉伸模量和泊松比；其次，利用经典层合板理论得到单元中压电片与基底板形成的三明治结构（在图1 单元中用A指示的部分）的等效材料参数；最后，结合有效介质理论确定整个单元的等效刚度。

首先研究单元中接入分流电路的压电片的等效材料参数。压电片可以视为各向同性薄板，基于平面应力状态假设和亚波长假设，其等效拉伸模量Ep和泊松比νp为

式中：Escp、νscp分别为短路时压电片的等效拉伸模量和泊松比为压电片拉伸机电耦合系数；d31为压电常数；εt33为常应力下介电常数；Cpt=为常应力下压电片固有电容；Ap为压电片面积

作为主体结构的单层板假设为各向同性材料，其抗弯刚度DB为

式中：Eb为板拉伸模量；νb为板泊松比；h为板厚。单元中被压电片覆盖的三明治结构部分A可视为3 层对称各向同性层合板，基于经典层合板理论，可得到A区域的等效抗弯刚度为

通过有效介质理论，结合A区域的等效抗弯刚度DA及其余区域B的等效抗弯刚度DB，可得整个单元的等效抗弯刚度Deff为

式中：χ=l2pl2b为压电片覆盖率为压电片短路时的抗弯刚度。

将表1 中电路阻抗的具体表达式代入式（5）中，即可得到压电片分别连接纯电感电路、负电容-电感串联电路以及负电容-电感并联电路时力电耦合超材料板的等效抗弯刚度。

2 负电容拓宽禁带的机制

以往关于电感分流力电耦合超材料梁的研究表明，电路的谐振效应导致超材料梁的等效抗弯刚度出现负值，从而产生禁带［23］。研究负电容对力电耦合超材料板等效抗弯刚度的影响效果，以此揭示负电容拓宽板中禁带的机制。

2.1 理论模型的验证和修正

在具体分析负电容拓宽禁带的机制前，需要对式（5）的准确性进行验证。具体方法为：将式（5）得到的等效抗弯刚度为负的频率范围与利用数值方法计算得到的禁带范围进行对比。禁带的数值计算方法介绍如2.1.1 节所述。

2.1.1 禁带的数值计算方法

根据复能带理论，波数有较大虚部的频率范围即可认为是禁带［24］。考虑力电耦合超材料板的周期性，利用布洛克理论（Bloch Theory），复能带的计算只需要使用图3 所示的单元。其中，ΩA和ΩB分别为压电片和基底板区域；St、Sb和Sl分别为压电片上电极（接分流电路）、下电极（接地）和压电片侧面。

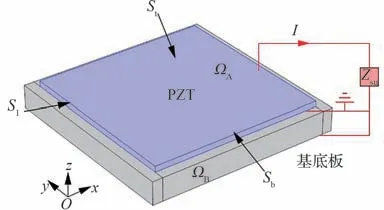
图3 单元示意图Fig.3 Representation of unit cell

在频域中，单元的波动控制方程为

式中：w为位移矢量；x为空间位置矢量；V为电极电压；ρ为密度；C为弹性张量；e为耦合张量；εs为常应变下介电常数张量；(·)T表示转置；∇symw=1 2(∇wT+w∇T)，控制方程式（6）需要满足的电场边界条件为

式中：D为电位移矢量；n为出平面方向单位法向量；q0为电路电荷。

根据布洛克理论，式（6）的解可假设为

式 中：k=k[cosθsinθ0]T=kΘ为 波 矢，k为 波 数；为布洛克幅值矢量，下标n表示第n个波模态；θ为波矢与x轴的夹角，代表波的传播方向。布洛克幅值是周期函数，也就是布洛克幅值具有以下周期特性：

式中：P=[P1P2]T为单元的周期性向量，P1、P2为单元在x、y方向上的长度；m为一整数。

将式（8）代入式（6）中得

将 式（10）投 影 到 测 试 函 数上 并 进 行 积分，结合边界条件式（8）、式（9），可获得弱形式：

式中：V0n，k为压电片上表面电极的电压；Ω表示整个单元区域，即压电片加基板；ε为格林应变张量；（）表示对应参数在测试函数中的投影。

利用有限元方法可将以弱形式表达的式（11）离散得到特征值求解方程：

式中：特征值λ=jk；矩阵M、H、K以及L的具体表达式可参见文献［25］。

给定波的传播方向θ，先针对不同的频率ω求解特征值问题式（12），然后利用关系k=-jλ即可得到频散曲线。

在低频范围，薄板中主要存在纵波、剪切波和弯曲波。以700 Hz 为例，图4 对比了这3 种波的振型，可见弯曲波的振动以出平面位移为主，而其他两种波以面内振动为主，因此确定弯曲波的筛选标准为

图4 纵波、剪切波和弯曲波的振型对比Fig.4 Comparison between vibration modes of longitudinal wave， shear wave and bending wave

式中：u、v、w分别为x、y、z轴方向位移。

根据筛选标准，从计算得到的曲线中分离出弯曲波的频散曲线，对其进行分析，找到波数虚部不为零的区域即为禁带。

2.1.2 理论模型准确性的验证与修正

假设压电片接入纯电感分流电路，覆盖率χ=0.8 时超材料板理论等效抗弯刚度为负的频率范围和有限元仿真得到的禁带范围的对比如图5（a）所示，其中k为弯曲波波数，Im（k）为波数的虚部，计算中使用的其他材料与几何参数见表2。从图5（a）中可以看出等效抗弯刚度为负的频率范围与禁带之间存在差异，这一差异可以通过修正理论固有电容消除。

表2 单元材料与几何参数Table 2 Unit material and geometric parameters

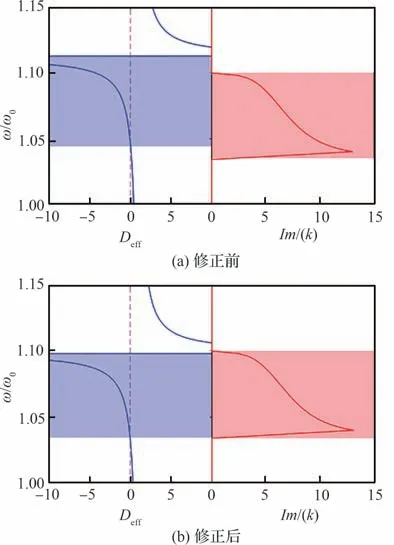
图5 纯电感分流电路中理论和数值禁带范围修正前后对比Fig.5 Comparison between theoretical and numerical bandgap before and after correction when only inductance is in circuit

假设修正后的固有电容为Cs*p=τCsp，τ为 固有电容的修正系数。通过调整τ的值，即可改变等效抗弯刚度为负的频率范围。等效抗弯刚度为负的频率范围中心与禁带中心重合时的τ值可作为修正系数。利用上述方法得到的修正系数τ=0.988。

图5（b）对比了修正后的负等效抗弯刚度范围和禁带范围，可以看出两者基本吻合，说明修正压电片电容后的理论模型能够准确的预测禁带的范围。

2.2 负电容对等效抗弯刚度的影响

不失一般性，以电感串联负电容电路为例来研究负电容拓宽禁带的机制。图6 对比了负电容具有不同取值时超材料板负等效刚度的频率范围，α=C0Csp为无量纲负电容值。可以看出，通过改变负电容的取值，有效地拓宽了负等效刚度的频率范围，因此能够获得更宽的禁带。为了设计负电容值获得想要的宽频禁带，第3 节将进一步分析负电容对禁带宽度和位置的调控规律。

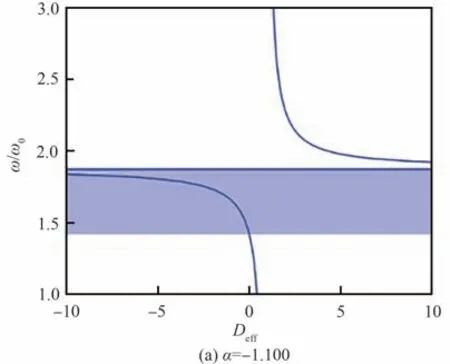
图6 负电容对负抗弯刚度范围的拓宽效果Fig.6 Broadening effect of negative capacitance on negative bending stiffness range

3 负电容对禁带范围的调控规律

3.1 负电容稳定区域

由于负电容是主动电路，在某些情况下会引起稳定性问题，在实际应用中必须避免。因此，在分析负电容对禁带范围的调控规律之前，必须先研究负电容的稳定区域。

力电耦合超材料板的稳定性条件为当ω=0时超材料板等效抗弯刚度为正。利用此稳定性条件即可获得负电容的稳定区域。结果表明，不管负电容与电感串联还是并联，其稳定区域都可用式（14）表示：

3.2 禁带范围的解析表达式

第2 节的研究结果表明，压电片固有电容修正后，理论获得的等效抗弯刚度为负的频率范围与禁带范围基本重合。因此，令式（5）中Deff＜0 得到压电片外接负电容-电感串联电路或负电容-电感并联电路时禁带范围的解析表式，可以用来方便的分析负电容对禁带范围的调控规律。

对于电容-电感串联电路，禁带范围的解析表达式如式（15）和式（16）所示，其中式（15）和式（16）分别对应负电容α位于左、右稳定区域的情况。对于负电容-电感并联电路，负电容α分别位于左、右稳定区域时，禁带范围的解析表达式为

从式（15）～式（18）可以看出，禁带范围与压电材料泊松比νscp、压电片拉伸机电耦合系数k31、刚度比γ、覆盖率χ以及负电容α这5 个无量纲参数有关。改变负电容α能够改变禁带范围和位置，具体的调控规律将在3.3 节分析。

3.3 禁带范围的电路参数分析

利用式（15）～式（18）来分析负电容值对禁带范围的调控规律，单元的材料和几何参数如表2所示。从式（15）～式（18）可以看出，压电片覆盖率χ=1 或者χ＜1 时，禁带上下界的表达式有较大的区别，说明覆盖率很可能显著影响负电容对禁带范围的调控规律。因此，考虑3 种不同情况下的压电片的长宽（26.0、30.1、33.6 mm，对应的覆盖率χ分别为0.6、0.8、1.0），探究不同覆盖率下负电容对禁带范围的调控规律。

首先研究负电容与电感串联的情况。当负电容α在左稳定区时，禁带上下界和宽度随负电容的变化规律如图7 所示。其中，图7（a）～图7（c）为 覆 盖 率χ分 别 为0.6、0.8 和1.0 时 禁带上下界的变化规律；图7（d）体现了3 种覆盖率下引入负电容对禁带范围的拓宽倍率。从图7 可以看到，随着|α|减小，即负电容向非稳定区靠近时，禁带的上下边界同时向高频移动，上边界比下边界上升的更快，导致禁带宽度增加。对比3 种不同覆盖率的情况可以看出，χ=0.6时拓宽倍率最高。

图8 为负电容α在右稳定区变化时对禁带上下界和宽度的影响规律。可以看出，随着|α|增大向非稳定区靠近，禁带上下边界同时向低频移动，下边界下降得更快，因此禁带宽度增加。对比不同覆盖率的情况可以发现，χ的大小主要影响禁带上边界随负电容的变化速度，χ越接近1，上边界随负电容的变化越不明显，能够产生的禁带越宽。值得注意的是在图8（d）中，χ=1.0 时拓宽倍率最高，与图7（d）中左稳定区域结果相反。

图7 串联且负电容位于左稳定区时禁带上下界和宽度随α 的变化规律Fig.7 Variation of bandgap upper and lower boundaries and width along with α when negative capacitance is in series and in left stable zone

图8 串联且负电容位于右稳定区时禁带上下界和宽度随α 的变化规律Fig.8 Variation of bandgap upper and lower boundaries and width along with α when negative capacitance is in series and in right stable zone

对于负电容与电感并联的情况，图9 和图10为α分别在左、右稳定区内变化时对禁带的调控特性。从图9 中可以看出，随着|α|减小，禁带宽度先增加后减小，负电容值存在一个最佳值使得禁带宽度最大。从图10 中可以看出，随着|α|增大，禁带上界增加，下界基本保持不变，因此，禁带宽度明显增加。覆盖率与拓宽倍率的规律分别与图7、图8 类似。

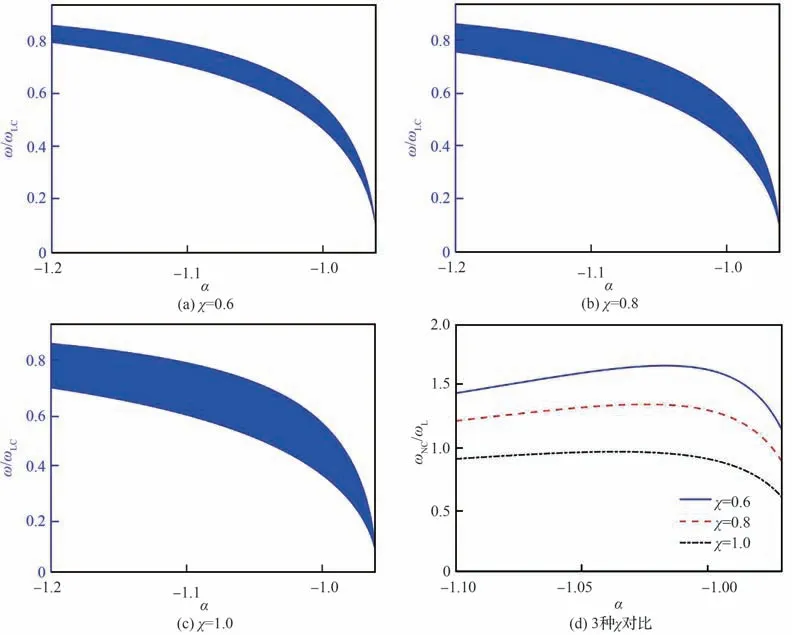
图9 并联且负电容位于左稳定区时禁带上下界和宽度随α 的变化规律Fig.9 Variation of bandgap upper and lower boundaries and width along with α when negative capacitance is in parallel and in left stable zone

图10 并联且负电容位于右稳定区时禁带上下界和宽度随α 的变化规律Fig.10 Variation of bandgap upper and lower boundaries and width along with α when negative capacitance is in parallel and in right stable zone

造成左右稳定区域覆盖率与拓宽倍率规律不同的原因在于：α位于左稳定区中时，纯电感禁带对覆盖率更为敏感，χ增加时负电容拓宽禁带的增长速度不如纯电感禁带，使拓宽倍率变小；α位于右稳定区中时则相反，负电容拓宽禁带对覆盖率更为敏感，χ越大，拓宽倍率越高。

由图7～图10 的结果可以看出：

1）负电容越靠近非稳定区，能够产生的禁带越宽，对于负电容电感串联情况，理论上禁带可拓宽10 倍以上，对于并联情况禁带可拓宽20倍以上。

2）为了得到宽频禁带，负电容既可以与电感串联也可以并联，负电容值即可从左稳定区选取也可从右稳定区选取，只要其取值在非稳定区附近即可获得较宽的禁带。

3）对于禁带宽度，压电片覆盖率越大，能够获得的禁带越宽；对于负电容电路的拓宽倍率，则需要根据稳定区域进行分析。工程中需要减振的频率范围一般是确定的，通过负电容设计即能满足要求，可以优化设计压电片的覆盖率使其最小化。

上述结论可用于指导力电耦合超材料板设计，实现低频宽带的减振效果。

4 低频宽带减振效果的数值验证

通过数值算例验证禁带的低频宽带减振效果。实际中，通常需要针对某一确定频段进行减振。第3 节的结果表明，要设计一个覆盖指定频率范围的禁带实现减振效果，负电容既可以与电感串联也可以并联。在下文的研究中以负电容-电感串联并且负电容值在右稳定区间为例，验证低频宽带的减振效果。

在COMSOL Multiphysics 软件中建立力电耦合超材料板的有限元模型，如图11 所示，包含6×6 个单元。单元中压电片覆盖率χ=0.9（对应基底板和压电片宽度lb=50 mm、lp=47.5 mm），其他参数与表2 中一致。在板中心a点施加垂直板面的简谐激励，研究b点的响应。

图11 力电耦合超材料板仿真模型Fig.11 Electromechanical coupled metamaterial plate model in numerical simulation

假设需要抑制板500～1 000 Hz 内的振动，也就是设计的禁带上下界分别为500、1 000 Hz。选择负电容-电感串联电路，并且负电容在右稳定区间。根据式（16）可以计算得到需要的电感和负电容分别为L=-0.07H、α=-0.6。实际中的电导线和器件不可避免存在电阻效果，因此，在有限元仿真中，在电路中引入一个电阻（R=50 Ω），与负电容-电感电路串联。

图12 为连接不同电路时b点位移的频响曲线，红色阴影部分为纯电感电路禁带范围，蓝色阴影区域为负电容-电感串联电路禁带范围。压电片短路的情况代表振动控制前的结果，纯电感电路代表未加入负电容时的响应，这两者均作为参考。对比分析可以看出，负电容-电感分流力电耦合超材料板能够在目标频率范围获得很好的振动抑制效果。

图12 不同电路配置下的频响曲线Fig.12 Response curves under different circuit conditions

5 结 论

针对航空结构低频抑振难题，通过将负电容电路引入力电耦合超材料板，推导了板等效抗弯刚度的解析表达式并进行了修正；研究了负电容对板中禁带的拓宽机制，表明负电容可以拓宽超材料板等效刚度为负的区域，从而实现禁带的拓宽；分析了负电容对禁带范围和位置的影响规律，表明负电容取值越靠近非稳定区域，产生的禁带越宽，对于负电容电-感串联情况，理论上禁带可拓宽10 倍以上，对于并联情况禁带可拓宽20倍以上；通过有限元算例证明引入负电容能够在低频范围内实现很好的宽频振动抑制效果。

利用禁带可以阻断振动传递路径达到减振的目的，例如，飞机发动机振动通过机翼向机身传递，将机身与机翼连接部位用本文提出的力电耦合超材料设计，阻隔机翼低频振动向机身的传递，可以显著降低机身振动，提高飞机的安全性和舒适性。