变转速工况下叶尖计时信号趋势项解析及验证
2023-04-19张旭龙王维民李天晴林昱隆艾信息王振国
张旭龙,王维民,,*,李天晴,林昱隆,艾信息,王振国
1.北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室,北京 100029
2.北京化工大学 发动机健康监控与网络化教育部重点实验室,北京 100029
获取叶片的振动参数是掌握叶片运行状态与功能特性的重要环节,可为在役叶片的运维及在研叶片的模型验证和设计改进提供数据支撑。基于应变片的测量可直接获取应变片粘贴位置的应力,测量结果可靠,然而难以实现全周期在线测量[1],通常作为一种实验研究的验证手段[2-3]。基于叶尖计时的非接触式测量方法作为一种最具潜力替代应变片法的叶片振动测量方法,近年来得到了广泛的研究和发展,不仅在航空发动机[4]、汽轮机[5]以及压缩机[6]叶片的振动监测中得到了应用,并且在转子系统故障诊断方面也表现出了应用潜力[7-8]。
叶尖计时法(Blade Tip Timing, BTT)通过安装在机匣上的传感器测量每个旋转叶片的实际到达时间,并将其与叶片不振动时的理论到达时间进行比较,根据两时间的差值来计算叶片的振动位移,对振动位移数据分析得到叶片振动参数,如振幅、频率、应力等[2-3]。随着叶尖计时技术工程化应用的推进,对于叶尖计时技术的研究,已经从原理性验证研究过渡为工程适用性研究。针对航空发动机等高端装备无键相参考或高分辨率键相信号获取困难的问题,国内外许多学者开展了无键相方法的研究,代表性的方法有到达时 间 拟 合 法[9-11]、参 考 传 感 器 法[12]、参 考 叶 片法[13]、复合参考法[14]、叶片间距变化法[15-16]。上述方法均是为传统叶尖计时技术中的键相参考寻找真实的或者虚拟的替代,用作参考基准进行叶片振动量的计算。无键相法由于没有叶片不振动的静态物理参考,因此处理结果中会弱化甚至丢失叶尖的稳态位移信息,即叶尖计时信号中的趋势项。针对实际装备非稳定工况下的准确测量问题,Fan 等[17]提出了一种广义正弦拟合法,以消除转速以低转速变化率(0.11 Hz/圈)线性变化时的影响。He 等[18]分析了叶尖计时法的误差因素并提出了改进的无键相方法,在离心压缩机叶片上进行了实验验证。Ren 等[19]分析了不同类型的转速变化对传统有键相法计算结果的影响,并提出了对应的修正方法。上述研究成果均降低了叶尖计时测量结果的不确定性,然而只考虑了转速线性变化引入的计算误差,并且只考虑了叶尖计时信号中存在的叶片共振时模态振型引起的瞬态位移,但是实测的叶尖计时信号中还存在难以量化评估的趋势项,目前针对趋势项的研究,均是围绕如何选择恰当的窗宽度去除趋势项,Russhard[20]研究了固定窗宽度的趋势项去除方法,给出了窗宽的经验值为200。刘志博等[21]针对变工况条件下定时信号趋势项去除问题,提出了趋势项自适应调节窗宽度拟合方法,从叶尖计时信号中直接去除趋势项保留模态振动信息,但并没有探明趋势项的来源,没有进行量化评估。
针对叶尖计时信号中趋势项的识别问题,从叶尖计时原理出发,分析了叶尖计时时域信号中可能存在的成分,推导了转速变化对趋势项的影响规律及辨识与修正方法。通过数值模拟研究证明了所提出的识别方法的有效性。然后,利用某发动机压气机叶片实测的叶尖计时数据及动应力数据进行关联分析,应用皮尔逊相关系数评估应变数据趋势项与叶尖位移趋势项的吻合程度,结果表明本文方法所得叶尖位移趋势项与动应变趋势项的皮尔逊相关系数为0.986,验证了所提方法的可靠性。最后,利用所提方法对某在研发动机风扇转子叶片的叶尖振幅进行分析,再次证实了叶尖稳态位移的存在。
1 叶尖计时方法
非接触叶尖计时测量原理如图1 所示,在转子叶片顶部机匣上安装叶尖计时传感器,叶片旋转经过传感器时会产生脉冲信号,经过计数器转换为到达时间,在与叶片同步旋转的转轴上安装键相(Once Per Revolution, OPR)传感器,键相到达时间作为计算叶片振动的参考基准并辨识叶尖计时数据所属的叶片。叶片不振动时,叶片到达传感器的理论时间可根据叶片在转子上的周向位置和转子的转速计算得到。假设叶片个数为nb,叶尖测点位置的旋转半径为R,键相信号触发时,沿周向第1 个经过叶尖计时传感器S1的叶片与键相参考的夹角为β1,则i号叶尖计时传感器测得的b号叶片在第n个旋转周期内的位移为
式中:为叶片的实际到达时间;为叶片的理论到达时间;fn为转子转频;α(OPR,i)为键相传感器与i号叶尖计时传感器之间的夹角;α(i-1,i)为相邻两叶尖计时传感器之间的夹角。
由以上原理可知,叶尖计时测量结果取决于转子转速、测点位置的旋转半径、传感器与叶片相对于键相参考的角位置。且叶尖计时测得的位移为转子叶片测点位置沿旋转方向的位移,或叶尖测点位置的位移沿旋转方向的分量[22-23]。叶尖计时信号的时域表达可以表示为
2 变转速对叶尖计时测量结果的影响
由第1 节理论可知,转速影响叶片理论到达时间及叶尖计时位移,并对不同周向位置的叶片引入不同的计算误差。从叶片旋转的角域展开,重点分析转速变化引起的测量误差及其辨识与剥离方法。b号叶片在第n个旋转周期内经过i号叶尖计时传感器时转过的角度为
叶片的运行转频可表示为
联立式(6)和式(7)可得:
式中:fOPR,n为第n个旋转周期键相信号触发时的转速,即第n个旋转周期的初始转速;为转速变化量,取值为0 时表示叶片恒速旋转,nk=1时为线性变速,nk>1 时表示非线性变速。有键相法计算叶片振动位移时,单个旋转周期内每个转子叶片的旋转速度为该旋转周期内的平均转速,即
将式(7)代入式(9),化简得:
因此有键相法计算得到的b号叶片在第n个旋转周期内经过i号叶尖计时传感器时转过的角度为
b号叶片与i号叶尖计时传感器之间的实际夹角可以通过低转速平稳运转时的数据标定得到[13-14],作为叶尖未发生位移的平衡位置参考,不会随叶片的运行状态变化,记为
忽略机匣振动引起的传感器移动,有:
有键相法计算得到的叶尖位移为
因此,叶尖测点位置真实位移沿旋转方向的分量为
有键相法的计算误差为
由式(16)可以看出,转速对有键相法的计算误差影响很大,且对不同位置的叶片引入不同的误差,叶片距离键相位置越远,计算误差越大。当叶片的瞬时转速与旋转一圈的平均转速相等时,有键相法的计算误差接近于零。因此当叶片转速升高至某一高转速时,叶片在该转速下旋转一圈的转速近似恒速,此时有键相法的计算结果中由于转速变化引入的趋势项接近于0。图2(a)为发动机试车台升速过程中低速状态下旋转一圈的到达时间信号,可以看出该旋转周期内转速不为恒速,叶片到达时间连线与键相到达时间连线之间的偏离程度可反映有键相法的计算误差分布情况。图2(c)中高转速下叶片的到达时间连线为直线,可以认为此时叶片旋转一圈的转速是恒定的。
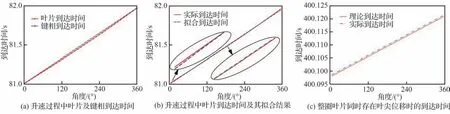
图2 发动机叶片实测的到达时间Fig.2 Measured arrival time of engine blades
无键相时,工程常用方法为对实测的整圈叶片的到达时间序列为因变量,叶片角度序列为自变量进行多项式拟合得到理论到达时间,转速也可通过拟合或多圈数据计算得到[9-11,14],即式(15)中的近似为0 时,有:
此方法的基本假设为叶尖位移引起的偏转角与叶片安装角度相比很小,叶片的理论到达时间与叶片位置满足多项式关系,多项式阶数取决于旋转一圈内的转速变化情况,恒速时采用线性拟合[9],变速时采用非线性拟合[11]。图2(b)为图2(a)中叶片到达时间及其线性拟合结果,可以看出拟合所得曲线与实际到达时间曲线存在偏差。因此,无键相法的误差一方面取决于多项式拟合方法,不同的拟合阶数将会对不同位置的叶片引入不同的误差,拟合所得的理论到达时间曲线与实际到达时间曲线交点位置附近的叶片误差最小。
当整圈所有叶片同时存在叶尖位移时,比如气动力、轴向窜动、转子热膨胀等引起的稳态位移[22-23],或者整圈叶片共振参数一致时,对所有叶片均会产生相同的Δt,此时整圈叶片的实际到达时间为
如图2(c)所示,这种情况相当于将叶片理论到达时间随叶片角位置的变化曲线沿时间轴平移,只改变多项式系数中的截距,拟合得到的理论时间与实际时间非常接近,导致无法有效识别出叶尖稳态位移。
3 转速变化引入的趋势项识别及叶尖位移修正
通过测得的实际到达时间准确计算叶片的转速及理论到达时间是保证叶尖位移计算精度的关键。由于叶片振动及稳态位移会引起叶片到达时间差,因此若用叶片到达时间数据计算转速会影响计算精度,以键相信号作为转速计算数据,依据式(15),键相的转动方程可表示为
m+1 圈键相数据可构造测量矩阵为
即:
式中:C为表示旋转圈数的矩阵,取值范围为(1,m);M为表示到达时间的矩阵;Ω为表示转速的矩阵。矩阵C可通过m的取值得到,矩阵M中包含键相到达时间及其指数项,为了消除轴振及测量噪声的影响,可以对键相到达时间先进行多项式拟合滤波再计算矩阵M[9-11,14],拟合阶数k取决于拟合优度[24],m的取值不能小于拟合阶数,本文中m取值为m=k+1。转速矩阵Ω可通过最小二乘法求出:
求得转速矩阵后,叶尖真实位移可通过式(15)直接求出。为了研究转速变化对叶尖计时信号趋势项的影响,依据式(16)中有键相法的计算误差,识别转速变化引起的趋势项,记为
判断叶尖计时信号趋势项是否为转速变化引起的计算误差的条件为
结合式(16),有键相法计算结果中转速变化引起的计算误差的修正方法为
工程上若要提高计算效率,可根据式(24)对趋势项进行判断,直接利用Savitzky-Golay 滤波器[22-25]或自适应滤波算法[21]去除转速变化引入的趋势项。式(15)及式(25)中的叶尖真实位移,包括了叶片的模态响应引起的叶尖振动位移以及轴向窜动、气动压力、转子热膨胀等引起的叶尖稳态位移,前者主要与叶片固有频率、激振力以及转速相关,通常规律性的出现在特定转速下(共振点),后者则受叶片转速、运行时间和运行环境参数的影响较大,如轴向移动、倾斜、扭转等稳态位移,可通过Savitzky-Golay 滤波进行剥离[22-23,25]。图3 为转速变化趋势项识别及叶尖位移修正流程。
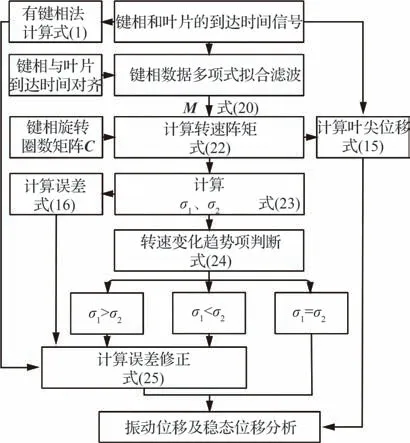
图3 转速变化趋势项识别及叶尖位移修正流程Fig.3 Flow chart of speed change trend term identification and tip displacement correction
4 仿真验证
建立融合转速变化、叶片同步振动位移及稳态位移的叶尖计时采样模型,假设振动位移与稳态位移的方向均沿旋转方向,叶片运动经过的角度为叶片旋转角度与叶尖位移引起的角度之和,叶片运动方程可表示为
仅考虑叶片的一阶振动位移与气动压力引起的叶尖稳态位移,两者均与转速有关,可表示为
式中:N为每秒的采样点数;dB(f)为叶片一阶弯曲位移[12-13];dL(f)为叶片旋转时气动压力引起的稳态位移,其与空气密度、叶片形状以及转速成正比;λ为比例系数,文中为了仿真叶尖计时信号中的稳态位移,用式(30)赋值。
叶尖计时传感器记录叶片到达时间的条件为
仿真参数如表1 所示,仿真4 种工况:①f(t)=2t+0.5t2,从0 Hz升速至100 Hz,dL(f)=0;②f(t)=2t+0.5t2,从0 Hz升速至100 Hz,dL(f)=0.002f;③f(t)=2t+0.5t2+0.2t3,从0 Hz升速至100 Hz,dL(f)=0;④f(t)=2t+0.5t2+0.2t3,从0 Hz升速至100 Hz,dL(f)=0.002f。
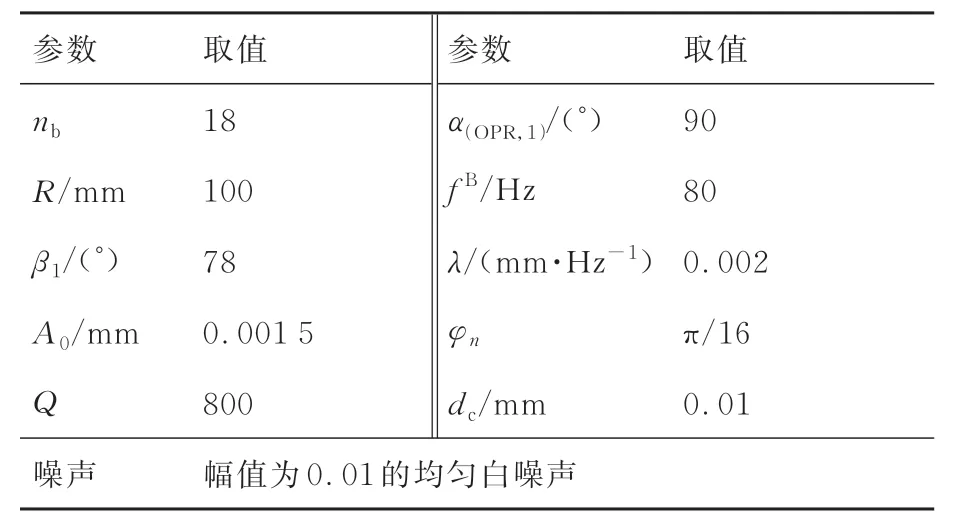
表1 仿真参数Table 1 Simulation parameters
利用传统有键相法、基于到达时间拟合的无键相法以及本文所提方法对仿真数据进行处理,图4 为4 种工况下1 号叶片、9 号叶片以及18 号叶片的位移及转速曲线,从图4 可以看出,不论何种工况下,本文所提方法计算的叶尖位移均与实际位移一致,不受转速变化情况与稳态位移的影响。有键相法的计算误差与叶片位置及转速变化情况有关,单个旋转周期内转速变化率越高、叶片位置离键相位置越远,有键相法的计算误差越大,当单个旋转周期内的转速接近恒速时,有键相法的计算结果接近于真实值,可以识别出叶尖的振动位移及稳态位移。无键相法的计算误差与叶片位置、转速以及叶尖位移大小均有关,四种工况下无键相法计算的叶尖位移均与实际值存在较大偏差,且是否存在稳态位移对无键相法的计算结果影响很小。计算整个升速过程中各方法计算结果与真实值差值的绝对值的平均值,得到不同工况下各方法平均误差随叶片位置的分布关系,如图5 所示,由于仿真工况为非线性升速,有键相法误差最大位置不为中间叶片,整体误差呈“倒U 形”分布,无键相法误差最小位置为拟合得到的直线与实际曲线的两个交点位置处,误差呈“W 形”分布,本文方法接近0误差。

图4 4 种工况下1 号叶片、9 号叶片以及18 号叶片的叶尖位移及转速Fig.4 Displacement and speed of No.1 blade, No.9 blade and No.18 blade under four working conditions
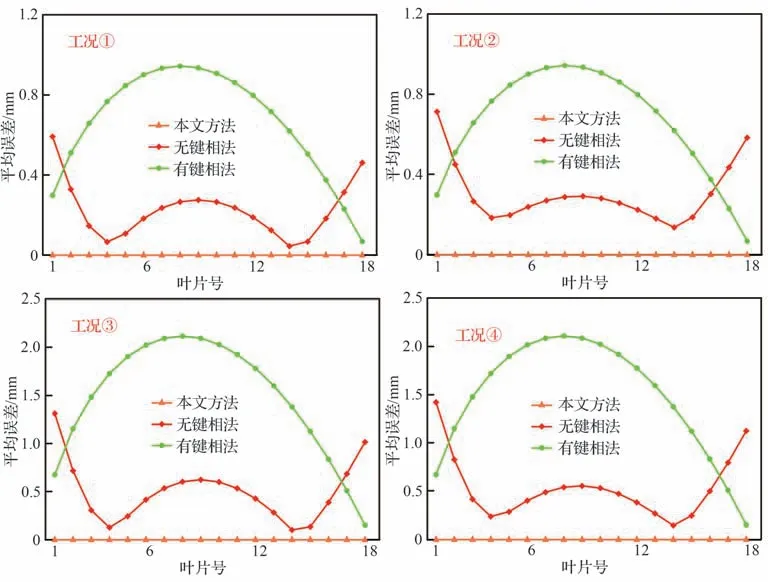
图5 4 种工况下不同方法的平均误差分布Fig.5 Average error distribution of different methods under four working conditions
5 实验验证
5.1 压气机叶片实验台验证
为了研究航空压气机叶片的振动特性,设计搭建了压气机叶片叶尖位移及动应力连续监测实验台,并完成了相关测试工作。实验台实物图如图6 所示,实验台由200 kW 双输出电机驱动,电机左侧输出端通过齿轮增速驱动超高速转子试验器,最高转速可达70 000 r/min 以上,电机右侧连接主轴箱驱动航空压气机整体叶盘。机匣下方搭配了丝杠滑块系统,通过步进电机驱动丝杠旋转,引导机匣沿轴向移动,可进行叶片轴向窜动、叶尖间隙变化及叶片-机匣碰磨等典型故障的模拟和诊断技术研究。实验台还配置了高速多路滑环引电器,叶片动应变信号通过滑环引电器输出至数采设备,在滑环引电器支架上安装了OPR 传感器,在机匣上安装了BTT 传感器,均为自主设计研制的常温光纤传感器,耐温200~300℃,传感器内部为七合一光纤束,光纤束采用金属铠甲护套进行保护,发射端及接收端均采用ST 接头与光纤延长线连接,探头采用M6 金属螺纹管封装,结构小巧,易安装,光斑尺寸小,定位精度高。整体叶盘包括37 个叶片,叶尖测点位置的旋转半径为276.5 mm,叶片旋转时,通过动态应变仪及自主开发的高转速叶片振动实时监测系统同步测量叶尖位移及动应变。

图6 压气机叶片叶尖位移及动应力连续监测实验台Fig.6 Test rig for continuous monitoring of compressor blade amplitude and dynamic stress
图7为 2 400~4 000 r/min 升速过程中不同方法处理得到的所有叶片的叶尖位移信号,由图7 可以看出,本文方法及有键相法处理得到的叶尖位移中均存在趋势项,且随转速的升高而增大,而无键相法处理得到的位移中不存在趋势项,这与前文理论及仿真分析结果一致。
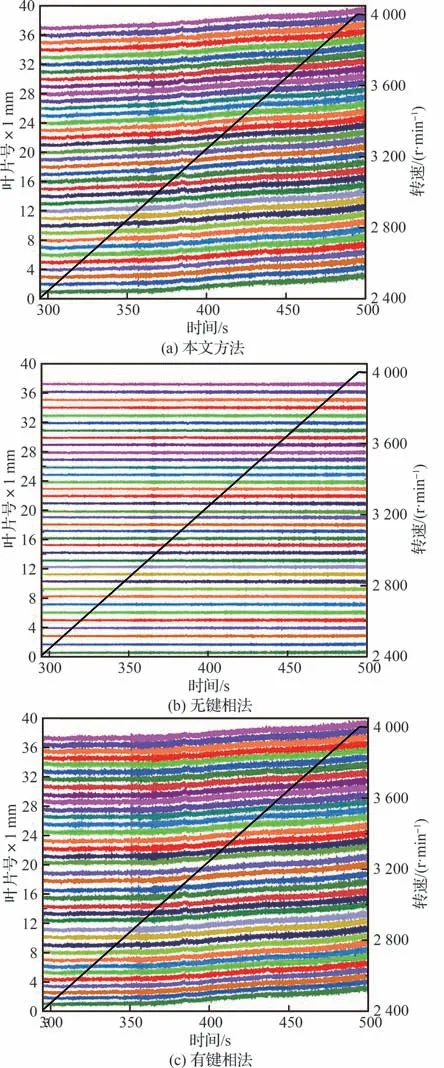
图7 3 种方法处理得到的所有叶片的叶尖位移Fig.7 Tip displacement of all blades obtained by three methods
具体的,18 号叶片的叶尖位移信号及对应的动应变信号如图8 所示,本文方法处理得到的叶尖位移与有键相法得到的不尽一致,为了证明本文方法处理结果的可靠性,将叶尖位移信号与动应变信号以时间为自变量进行关联分析,由于叶尖计时测得的位移为叶尖测点位置沿旋转方向的位移,而文中的叶片不为弦线平行于转轴的直板叶片,叶尖位移不沿旋转方向,因此在分析前将叶尖位移信号转换为叶尖测点位置的倾斜量[23]。考虑到叶片旋转时离心力也会导致应变及叶尖位移的增加,利用ANSYS 计算了轮盘在转速4 000 r/min 时的离心应变及总变形,如图9所示,可以看出4 000 r/min 时叶片离心应变最大值为6.34 με,叶尖位移的最大值为4 μm,与图8中实测的叶尖位移及动应变相比可以忽略不计,并且整体叶盘旋转时无其他外力作用,因此可以认为图8 中叶尖位移及动应变的趋势项是气动阻力导致的叶片倾斜引起的。由于单个传感器的叶尖位移信号的采样率为转速频率,与动应变信号的采样率相差太大,难以逐点量化分析两者之间的关系,本文首先计算相邻两个叶尖位移采样时刻之间的动应变的平均值,然后进行SG 滤波求取趋势项,应用皮尔逊相关系数[26]评估动应变数据趋势项与叶尖位移趋势项的吻合程度,相关系数越接近1,则表明两信号关联程度越高,有键相法及本文方法的处理结果如图10 所示,本文方法所得位移的皮尔逊相关系数为0.986,有键相法的为0.969,表明本文方法处理的叶尖位移结果更加准确可靠。
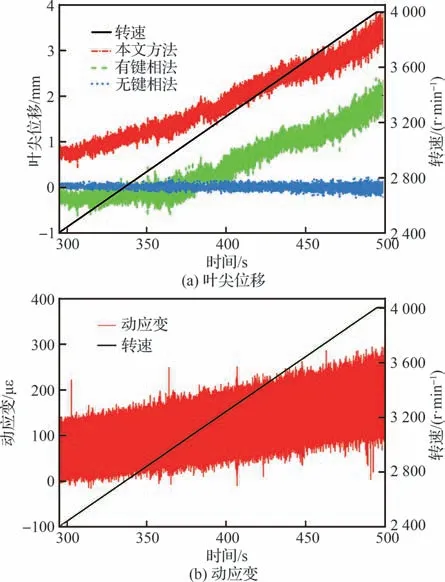
图8 18 号叶片的叶尖位移及动应变Fig.8 Tip displacement and dynamic strain of 18th blade
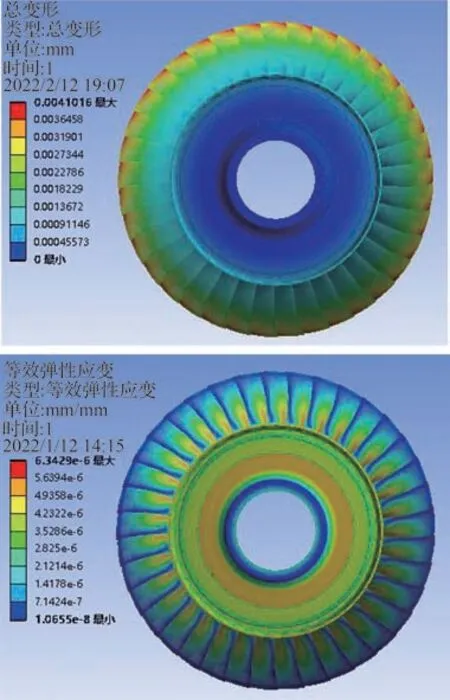
图9 4 000 r/min 下的离心应变及位移Fig.9 Centrifugal strain and displacement at 4 000 r/min
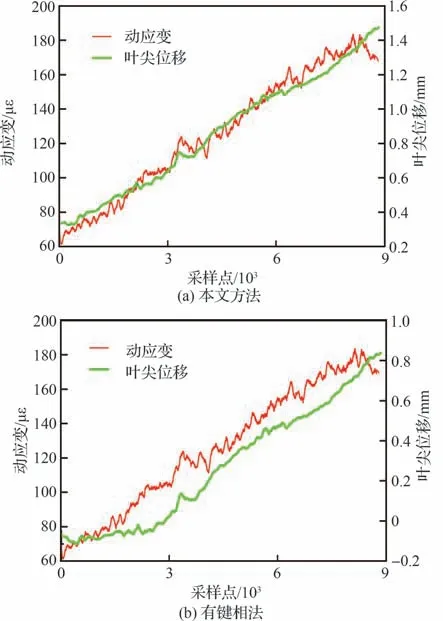
图10 叶尖位移趋势项及动应变趋势项Fig.10 Tip displacement trend term and dynamic strain trend term
5.2 航空发动机风扇叶片数据分析验证
采用非接触叶尖计时法对某在研发动机风扇转子叶片性能测试过程中的叶尖振幅进行监测,图11 为两次阶梯升速过程中所有叶片的叶尖位移信号,由图11 可以看出,本文方法及有键相法分析结果中存在趋势项,且随转速变化而变化,可以定性为气动压力引起的叶尖稳态倾斜,进气口压力恒定时,叶尖稳态倾斜量与转速成正比例增加,而无键相方法分析结果中不存在明显的趋势项。
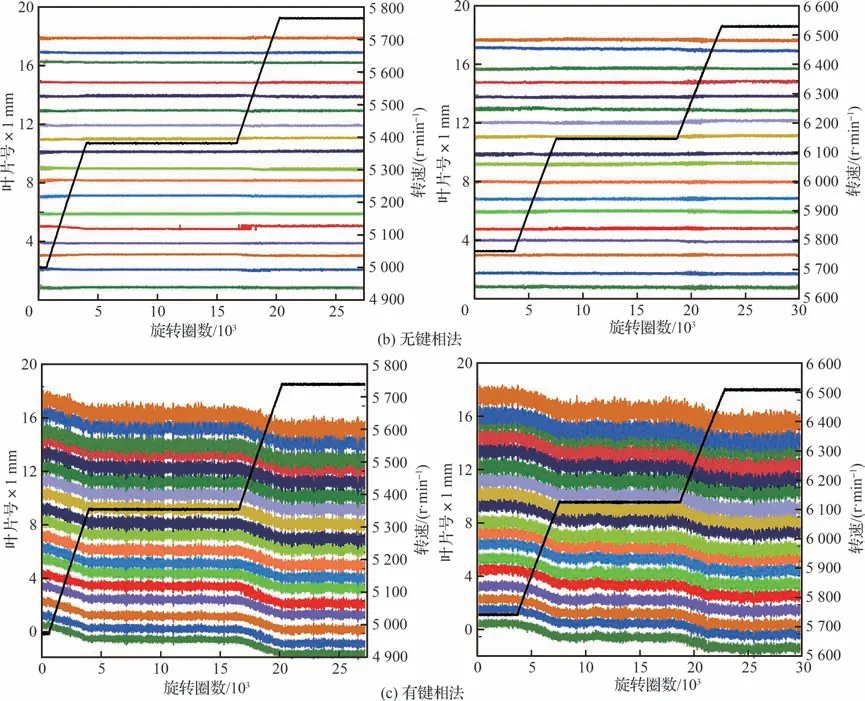
图11 发动机风扇叶片叶尖位移信号Fig.11 Engine fan blade tip displacement signal
图12为两次阶梯升速过程中3 种方法处理得到的1 号叶片、9 号叶片、18 号叶片的叶尖位移信号,可以看出,本文方法得到的1 号叶片的位移与有键相法的计算结果接近一致,随着叶片编号的增加,有键相法计算结果的峰峰值越来越大,但趋势项保持一致,这可能是由于轴系振动导致单个旋转周期内转速表现为恒定值加波动噪声的效果,使得有键相法计算得到的叶尖位移数据也存在噪声,并且随着叶片到达时间与键相到达时间的差值的增加,叶尖位移中的噪声也越大。图12 结果表明,本文方法计算得到的每个叶片的叶尖位移的峰峰值没有明显的差别,因此可以说明本文所提方法不仅能够准确识别叶尖计时信号中的趋势项,还可以弱化轴系振动或转速波动引起的测量噪声。
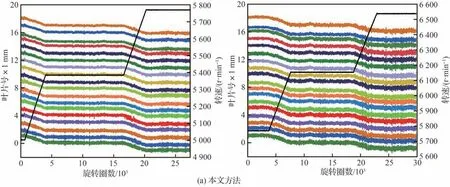
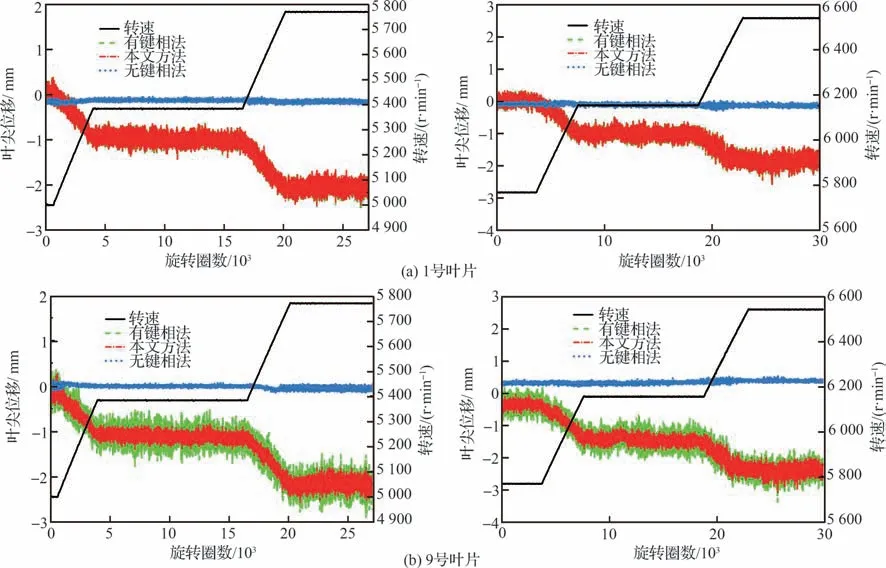
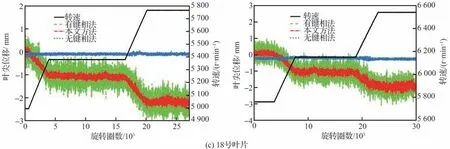
图12 1 号叶片、9 号叶片、18 号叶片的叶尖位移Fig.12 Tip displacement of 1st, 9th and 18th blade
6 结 论
1)叶尖计时技术可以监测叶片的振动位移以及稳态位移,传统有键相法及基于到达时间拟合的无键相法的计算结果受变速加速度的影响较大,叶片旋转一圈内的转速不为恒速时存在计算误差,误差大小与叶片位置及转速有关。
2)建立了融合转速变化及气动阻力引起的趋势项的叶尖计时数字模型,仿真结果表明,本文方法的计算值与设定值一致,可以准确识别出叶尖的振动位移及稳态位移。
3)实验结果表明,本文方法计算的叶尖稳态位移与稳态应变的相关系数为0.986。与传统有键相法相比,本文方法还能弱化轴系振动或转速波动引起的测量噪声。
