朴素传幽真 通法蕴高见——对2022年浙江卷与北京卷解析几何题的思考

贺 旭

(浙江省宁波市北仓明港高级中学)

2022年的浙江卷和北京卷解析几何大题非常相似,都是考查直线与椭圆位置中的距离问题,通过设点、设线,将未知点转化为已知点,用点参法或线参法表示距离.试题起点低,注重通性通法,主要考查学生的逻辑推理和数学运算核心素养.从表面上看,这两道题基础而朴素地考查了学生的解析几何基本功,但细细揣摩,透过表象看本质,这两道题都隐含着极点极线的数学背景.

1 试题呈现

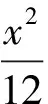
(Ⅰ)求点P到椭圆上点的距离的最大值;

(Ⅱ)求|CD|的最小值.

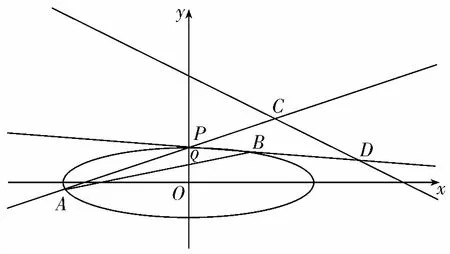
【分析】点与直线是解析几何中最基本的要素,高考题注重通性通法,最直接的解题思路就是设点或者设线,本题中涉及到的点有A,B和C,D,直线有lAP,lBP.由此可以从以下三种方案解题.

方案1:设点A,B,求点C,D;

方案2:设点C,D,由A,Q,B三点共线,求解;

方案3:设lAP,lBP,求点C,D.

(Ⅱ)方案1:设点A(x1,y1),B(x2,y2),

消去y整理得(12k2+1)x2+12kx-9=0,

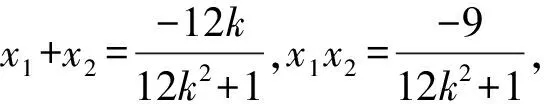
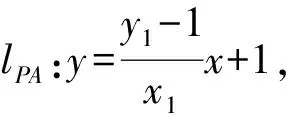
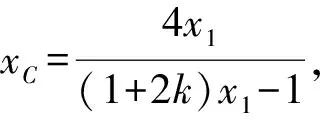
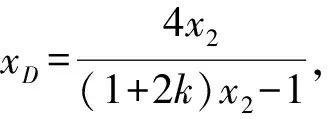
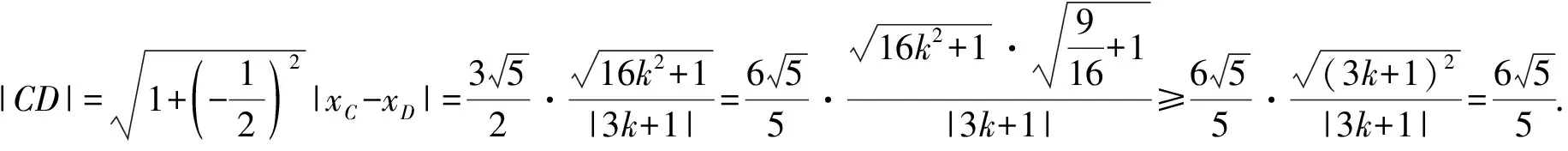
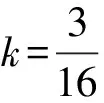
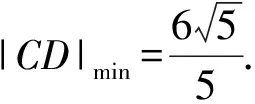
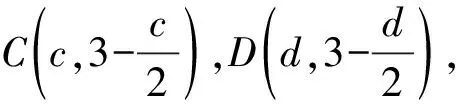
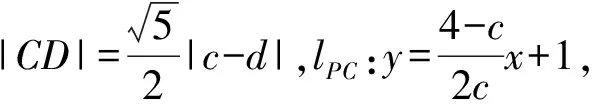
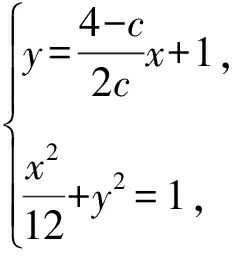
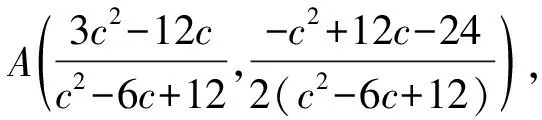
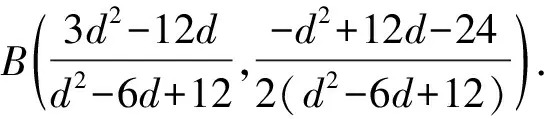
因为A,Q,B三点共线,

所以易知5cd-18(c+d)+72=0,

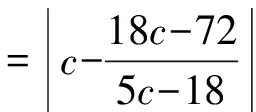
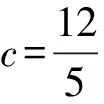
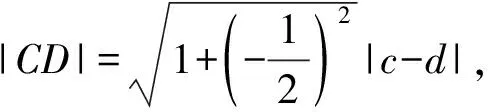
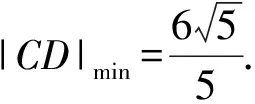
方案3:设lAP:y=k1x+1,lBP:y=k2x+1,

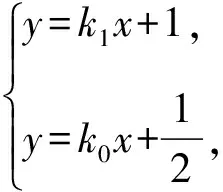
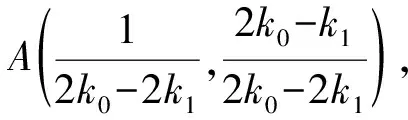
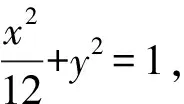
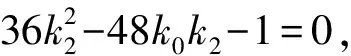
则k1,k2是方程36k2-48k0k-1=0的两根,

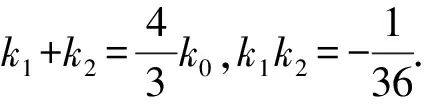
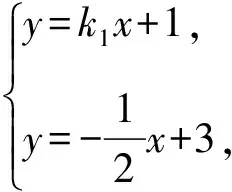
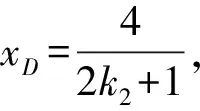
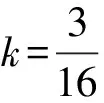
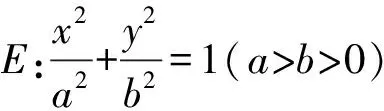
(Ⅰ)求椭圆E的方程;

(Ⅱ)过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B,C,直线AB,AC分别与x轴交于点M,N,当|MN|=2时,求k的值.

【分析】本题涉及到的点有B,C和M,N,直线有lAB,lAC.由此可以利用以下三种方案解题.

方案1:设点B,C,求点M,N;

方案2:设点M,N,由P,B,C三点共线求解;

方案3:设lAB,lAC,求点B,C.

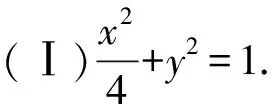
(Ⅱ)方案1:设B(x1,y1),C(x2,y2),lBC:y=k(x+2)+1,

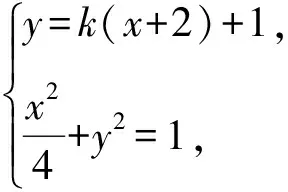
得(1+4k2)x2+(16k2+8k)x+16k2+16k=0,

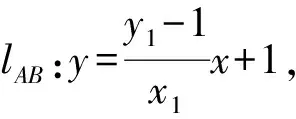
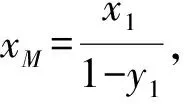
所以|MN|=|xN-xM|

=2,

解得k=-4.

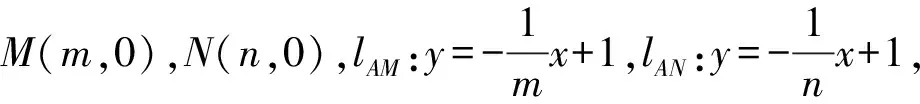
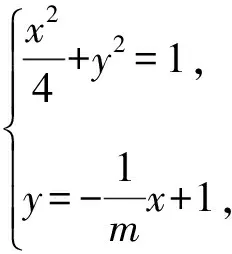
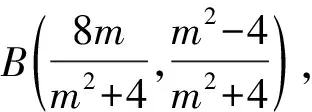
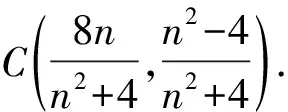
因为P,B,C三点共线,

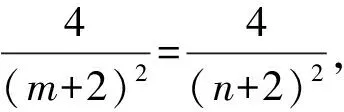
所以m+n=-4.

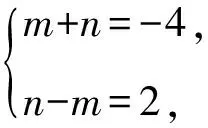
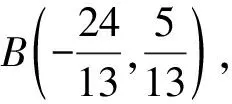
方案3:设B(x1,y1),C(x2,y2),lAB:y=k1x+1,lAC:y=k2x+1.

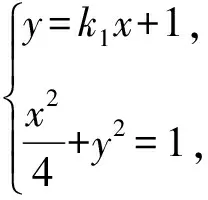
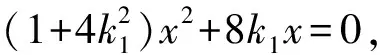
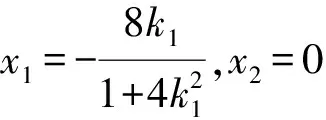
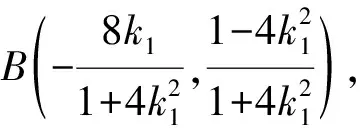
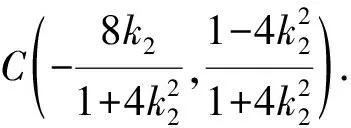
因为P,B,C三点共线,所以kPB=kPC,

即(k1-k2)(k1+k2-4k1k2)=0.

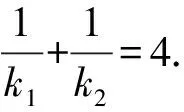
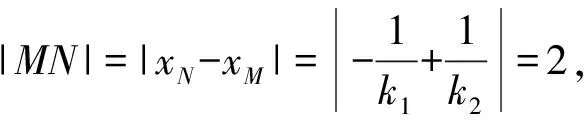
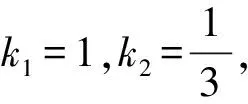
所以k=-4.

2 思路剖析

卷区思路难点浙江卷方案1:设点A(x1,y1),B(x2,y2),直线lAB:y=kx+12,与椭圆方程联立,借助韦达定理得出x1,x2之间的关系,用x1,y1,x2,y2表示xC,xD,从而用k表示|CD|①|CD|表达式化简繁琐;②|CD|=352·16k2+1|3k+1|目标函数求最值困难方案2:设Cc,3-c2(),Dd,3-d2(),表示出|CD|,由PC,PD的直线方程与椭圆方程联立,求出点A,B的坐标,再根据A,Q,B三点共线,求得c,d关系式,从而求解|CD|①A,Q,B三点共线,化简运算量大;②|c-d|=c-18c-725c-18目标函数求最值困难方案3:设lAP,lBP,联立直线AP,AB,用k1,k0表示A点坐标,用k2,k0表示B点坐标,得出关于k1,k2的同构式,借助韦达定理求出k1,k2的关系,从而用k1,k2表示xC,xD,从而求解|CD|①难以发现k1,k2的同构关系;②|CD|=352·16k20+1|3k0+1|目标函数求最值困难

【评析】总体来说2022年浙江卷与北京卷有异曲同工之处,解法思路基本一致,从最基础的设点、设线入手,用点参法或线参法表示距离.从难度上看,浙江卷更难些,涉及求距离的最值问题,需要换元、不等式或者求导等知识储备,北京卷则是直接求值,简洁直白.

研究高考题的目的不仅仅是解题,更是探寻题目背后的本质,那么浙江卷与北京卷这两道解析几何题有没有什么共同的背景呢?

3 背景探究

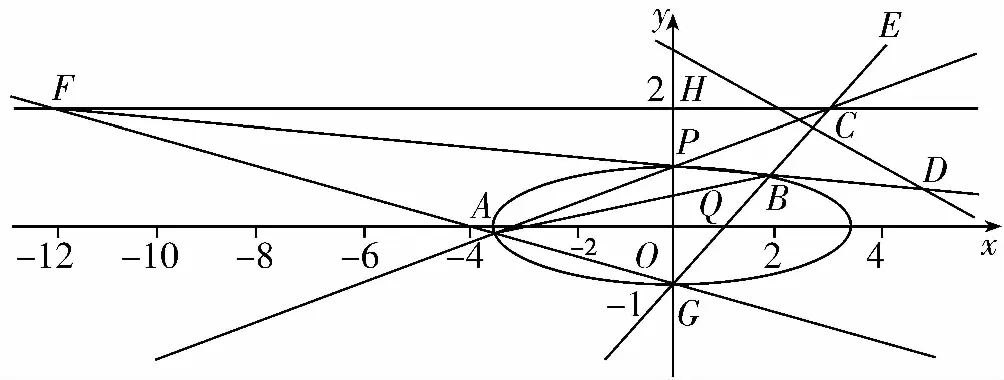
若是能看出这道题中隐含的极点极线模型,就能知道直线AP与直线BP的斜率之积为定值,那就可以选择方案3,胸有成竹地突破其中的难点①.

北京卷的解析几何题也有极点极线的影子,点P的位置特殊,方案3中的直线AB,AC斜率的倒数之和是定值,这是巧合,还是必然?将北京卷的这道题进行一般化处理后,再进行探究.

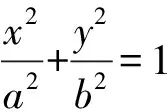
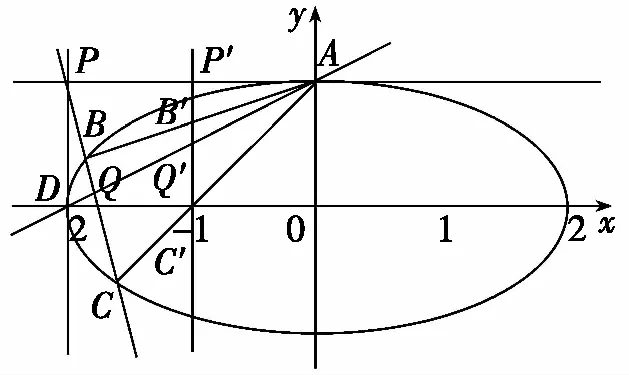
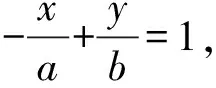
与直线PB交于Q,点P,Q,B,C为调和点列,

直线AP,AQ,AB,AC为调和线束.

作一条垂直于x轴的直线,

分别交直线AP,AQ,AB,AC于P′,Q′,B′,C′,

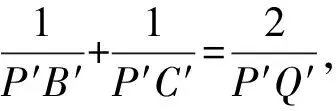
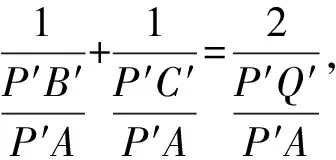
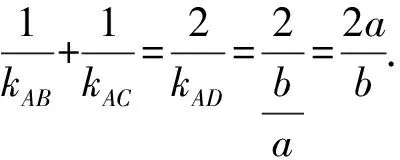
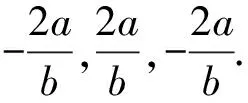
有了这个结论,北京卷这道题可以大胆地选择方案3,难点也将迎刃而解.

4 研题反思

解析几何是用代数的方法研究几何问题,代数方法在圆锥曲线中体现为运算,运算不仅仅是简单地计算,它包含运算技巧与逻辑推理.面对圆锥曲线问题,学生常常会望而生畏,但是老师上课一讲,又觉得好像也不难,设几个点、几条线,也就算出来了,没什么玄机,那为什么就那么难学呢?

第一个原因是难以确定研究对象.圆锥曲线中点、线很多,设哪些点、设哪些线,学生常常很迷茫,不知如何下手.浙江卷与北京卷这两道题很典型,以浙江卷为例,点A、点B是一对点,点C、点D是一对点,设了点A的坐标,则点C的坐标自然就有了,同理可得点B、点D的坐标.做题前,先仔细审题,分析圆锥曲线中的几何元素,思考有关联的点与线,再下手.

第二个原因是难以确定运算方向.设点、线后,往往需要与圆锥曲线联立,得到相对应的点、线,但学生往往不敢算下去,被略微复杂的形式吓唬住,譬如浙江卷中设点A,将直线PA与直线CD联立后,得到点C形式上必然是复杂的,|CD|的表达式更是繁杂,但只要心中确定了运算方向,就应该坚定不移地运算下去,犹豫不决,半途而废肯定是不会成功的,何不勇往直前,放手一搏.