作业的“精练”变式设计
——以微专题“解三角形中范围(最值)”作业设计为例
2023-04-15杜海洋
杜海洋 李 平
(成都经济技术开发区实验中学校)
随着新课改在全国范围内的全面实施,“高效课堂”成为时代主流.为了使教学效果达到高效,课堂上的“精讲”、作业的“精练”成为教学的追求目标.为了反馈课堂教学效果,检验的手段“课后作业”成为至关重要的一环,其中课后作业质量的高低,即作业“精练”的设计就凸显其重要性.
变式不仅是指问题的变式,而是泛指知识形成过程中的问题设计;基本概念辨析型变式;定理、公式的深化变式,多证变式及变式应用;例题、习题的一题多解、一法多用、一题多变、多题归一等,其中课后作业中如何设置变式“问题”才能达到最终检测目的,即变化中的“不变性”,笔者认为作业设计的变式及思维“梯度”是变式设计的关键.在高中数学知识体系中,解三角形是一个基础知识点,也是高考的一个高频考点.在解三角形的题型中,主要考查正弦定理和余弦定理的应用,而在解三角形中涉及求面积、周长、角等最值和取值范围是命题的热点,也是重点、难点.笔者在高三复习时通过微专题对本专题即解三角形的范围(最值)的方法进行优化归纳,并给出针对性巩固练习,以期求得热点、难点的突破.下面笔者以微专题“解三角形中范围(最值)”作业设计为例,以飨读者!
【作业题根设计】
作业“首题”的选择是作业设计的核心,因为它要起到承上启下的作用,要为本节作业内容开篇起到“引领”作用,俗话说“一个典型的事例胜过千万句空洞的说教”,一是要回归基本知识,二是要体现基本方法.
【题根变式设计】
变式设计一般遵循学生的最近发展,尤其是在“题根”的基础上对其条件、结论、结构、方法等进行“变式”,笔者认为变式试题的条件和结论尽可能做到“螺旋式上升”的策略,让学生在前面的基础上“跳一跳,摘得到”.
【题根】(高考真题理)△ABC在内角A,B,C的对边分别为a,b,c,已知a=bcosC+csinB.
(Ⅰ)求B;
(Ⅱ)若b=2,求△ABC面积的最大值.
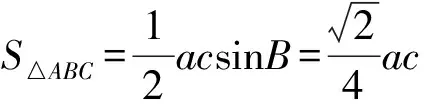
【变式1】在△ABC中,sin2A-sin2B-sin2C=sinBsinC.
(Ⅰ)求A;
(Ⅱ)若BC=3,求△ABC的周长的最大值.
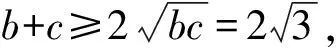
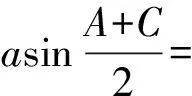
(Ⅰ)求B;
(Ⅱ)若△ABC为锐角三角形,且b=2,求△ABC周长的取值范围.
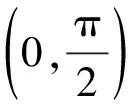
【变式3】将变式2的第(Ⅱ)问变为(Ⅱ)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.
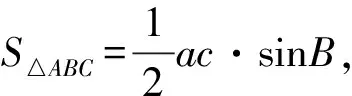
即通性通法出场,目的进一步强化解三角形的核心方法为将目标表达式转化为角的函数.有了化角意识可让学生利用此法去解变式1即变式1,方法2:边化角消参化单变量.
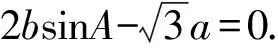
(Ⅰ)求角B的大小;
(Ⅱ)求cosA+cosB+cosC的取值范围.
【设计意图】(Ⅰ)问根据已知条件,利用余弦定理经过较复杂的代数恒等变形求得a2+c2-b2=ac,对运算能力要求较高;利用正弦定理边化角,运算简洁,是解三角形常用的方法,确定为最优解;(Ⅱ)问可运用多种方法,利用余弦定理角化边代入化简,运算较为麻烦,其次直接使用三角恒等变换,将化为角的三角函数进行求值,简洁明快,确定为最优解.此训练题设计目的是让学生对比解法,识别题型,建立解题“模式”.
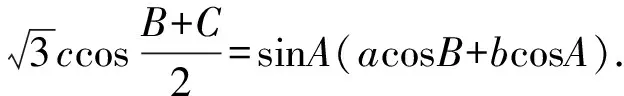
(Ⅰ)求A;
(Ⅱ)若b=1,求c的取值范围.
【设计意图】此题考查解三角形的综合应用,能够根据题干给出的信息选用合适的余弦定理公式是解题的第一个关键;根据三角形内角A+B+C=π的隐含条件,结合三角函数的诱导公式及正弦定理,将问题转化为求解含∠A的表达式的最值问题是解题的第二个关键,注意角的限制范围.
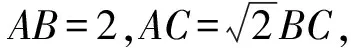
【设计意图】在处理三角形中的边角关系时,通法为把所求目标式转化为关于角的函数关系,或化归为边的关系.题中若出现边的一次式一般利用正弦定理,出现边的二次式一般为“代数化”埋下伏笔,即坐标系的运用,拓展学生思维.
【答案及解析】
【题根解析】(Ⅰ)解法一:
因为a=bcosC+csinB,
所以由正弦定理得
sinA=sinBcosC+sinCsinB.①
在△ABC中,A=π-(B+C),
所以sinA=sin(B+C)=sinBcosC+sinCcosB.②
由①和②得sinBsinC=cosBsinC.
因为sinC≠0,所以sinB=cosB.
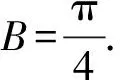
解法二:因为a=bcosC+csinB,
所以由余弦定理的推论得
即a2+c2-b2=2acsinB,
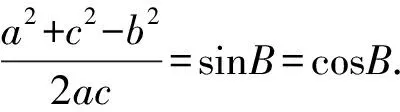
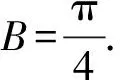
由已知及余弦定理得
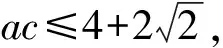
当且仅当a=c时,等号成立,
则△ABC面积的最大值为
【变式1】【解析】(Ⅰ)在△ABC中,设角A,B,C的对边分别为a,b,c.
由正弦定理得a2-b2-c2=bc,
由余弦定得的推论得
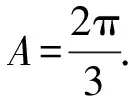
(Ⅱ)由余弦定理得
a2=b2+c2-2bccosA=b2+c2+bc=9,
即(b+c)2-bc=9.
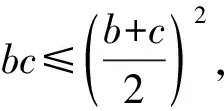
当且仅当b=c时,等号成立,
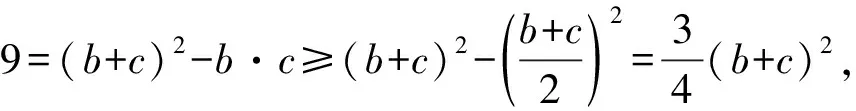
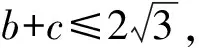
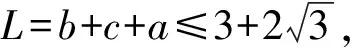
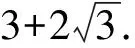
【变式2】【解析】(Ⅰ)由正弦定理得
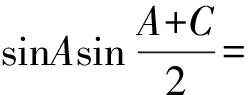
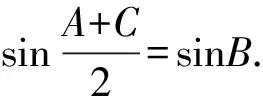
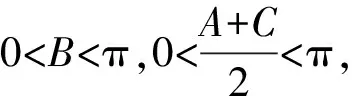
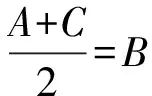
根据题意知A+B+C=π,
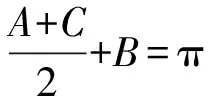
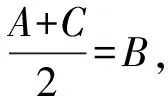
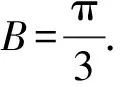
(Ⅱ)解法一:正弦定理消参化单角函数
所以△ABC的周长
L=a+b+c
因为△ABC为锐角三角形,
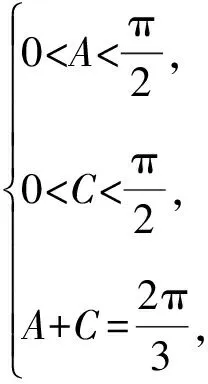
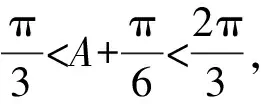
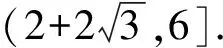
解法二:图形分析法
易知当B为优弧AC的中点即B1处时,
△ABC的周长和面积最大,
设△ABC的周长为L,此时L=2×3=6,
当△BAC为直角三角形时,
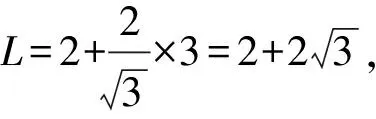
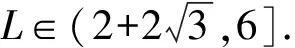
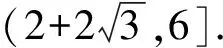
【变式3】【解析】(Ⅱ)解法一:因为△ABC是锐角三角形,
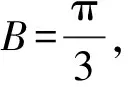
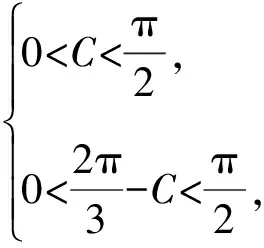
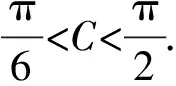
由三角形面积公式得
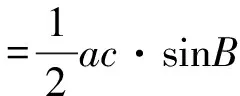
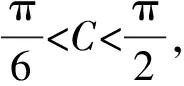
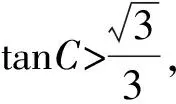
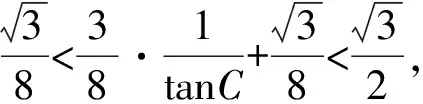
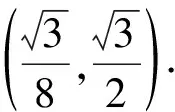
解法二:由余弦定理得b2=a2+1-a.
因为△ABC是锐角三角形,
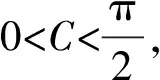
将b2=a2+1-a代入a2+b2-1>0得2a2-a>0,
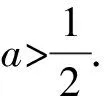
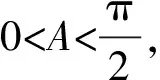
所以b2+c2-a2>0,
将b2=a2+1-a代入b2+1-a2>0得a<2,
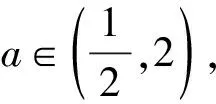
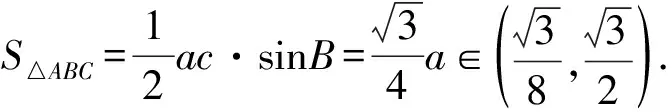
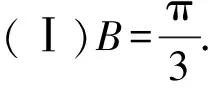
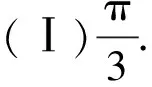
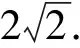
【作业变式设计】
【要点反思】
1.知识点:解三角形的相关知识,涉及到正弦定理边角互化的应用、余弦定理及推论的应用、三角形周长、面积等最值(范围)的求解问题.
2.解题思路运用:常规方法涉及方法1基本不等式、方法2边化角,进而转化为正弦函数求最值问题,其本质为转化化归消参策略.
3.整个作业变式设计在题型和方法上采用螺旋式上升的策略,步步设卡,而不是一下套用所谓的巧法或“秒杀”,整个过程学生思维得到锻炼,弄清问题的来龙去脉,知识生成得到很好的训练.
【体会】
作业是检查学生对基础知识、基本技能掌握程度的一种必不可少的有效手段.在作业设计中,要面向全体学生,尊重个体差异,树立分层递进的教学观.在作业设计时,要根据学生的不同层次需求设计不同的练习,才能使学生在学习中达到事半功倍的效果.数学教与学的活动不仅是对原题解法上的探求,更是在原题的基础上实现解法或认知的延伸与拓展,挖掘出更深刻的本质与结论.变式教学与作业设计则都要能凸显概念的本质,突出问题特征,揭示知识的关联,让课堂教学效果更加高效.
近年的高考试题坚持“新题不难,难题不怪”的命题方向,强调“注意通性通法,淡化特殊技巧”,多数高考试题能在课本或往年高考真题中找到“原型”,不少高考题就是对课本原题或往年高考真题的变形、改造及综合.尤其在高考复习备考中,节奏快、时间紧、容量多、内容跨度大、抽象性强,在这样的环境下,教师更是迫切需要提高课堂效率,实现高效课堂,不是简单地增加“刷题”量,而是需要教师对典型例题精心准备,充分挖掘,利用变式教学和课后作业精心设置的“精练”,让学生更好地理解问题的实质,从而实现触类旁通,举一反三,达到事半功倍的效果.
