源于教材 提炼模型 灵活应用
——平面向量极化恒等式及应用探究
2023-04-15谢亚强
谢亚强
(甘肃省镇原县孟坝中学)
在高考考查平面向量的试题中,数量积问题有着举足轻重的地位,一直都是高考命题的重点和热点.求解平面向量数量积问题的常规解题思路:一是依据长度和夹角(定义),二是利用坐标运算.而对于一些具有中点或能够构造中点的向量的数量积问题,应用平面向量的“极化恒等式”求解,则可以缩短思维线路,减少运算量,尤其是对于一些数量积的客观试题可谓是“秒杀”!“极化恒等式”是源于教材中的一道练习题,本文就从这道练习题说起,提炼平面向量的“极化恒等式”的两种模型,并通过有关高考题中的“常规解法”与“极化恒等式”解法的比较,体会“极化恒等式”解题的灵活性和解法的优越性.
一、课本题目
2019版普通高中教科书A版数学必修第二册第22页练习3.求证:(a+b)2-(a-b)2=4a·b.
证明:因为(a+b)2=a2+2a·b+b2①,
同理:(a-b)2=a2-2a·b+b2②.
所以①-②得(a+b)2-(a-b)2=4a·b.
二、极化恒等式及其几何模型
1.极化恒等式

我们称这一公式为平面向量的“极化恒等式”,它建立起两向量的数量积与两向量的和、两向量的差三者之间的等量关系,可以“知二求一”.
平面向量的“极化恒等式”是用来解决起点相同的数量积问题,分为三角形模型与平行四边形模型.
2.极化恒等式三角形模型

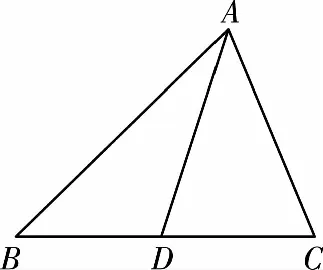


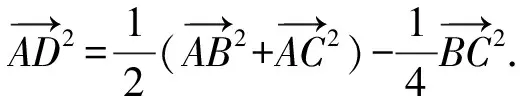
3.极化恒等式平行四边形模型
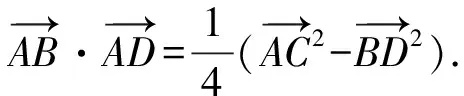
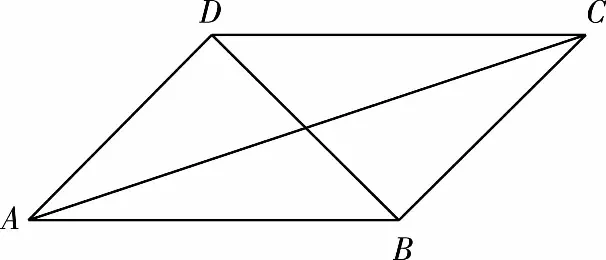
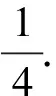

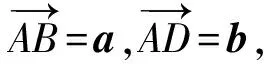



三、极化恒等式的应用
极化恒等式是将两个非零向量的数量积转化为这两个向量的“和向量”与“差向量”,所以当两个向量的“和向量”与“差向量”均为已知向量时,可以考虑应用极化恒等式进行转化.特别是在求解有中点或能够构造中点的向量的数量积问题时,极化恒等式有着很好的应用.下面以三道高考题为例,通过应用常规解法与应用极化恒等式的解法比较,来说明极化恒等式在求解有关平面向量数量积客观性问题的优越性.
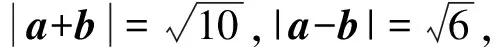
( )
A.1 B.2 C.3 D.5

所以(a+b)2=a2+2a·b+b2=10 ①,

所以(a-b)2=a2-2a·b+b2=6 ②,
所以①-②得4a·b=4,所以a·b=1,
故选A.

点评:常规解法相当于推导了一次“极化恒等式”后求解,而后者直接利用“极化恒等式”结论代入解答,可谓快速、简捷、“秒杀”.

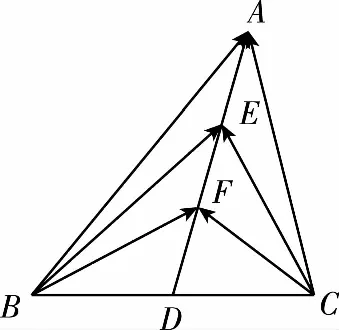
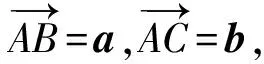

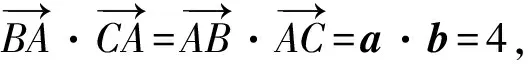
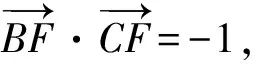
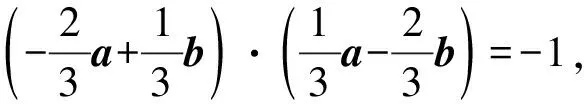
展开整理得-2(a2+b2)+5a·b=-9,
所以-2(a2+b2)+5×4=-9,



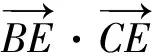
常规解法2.(坐标法)如图,以BC所在直线为x轴,D为坐标原点,建立平面直角坐标系xDy.
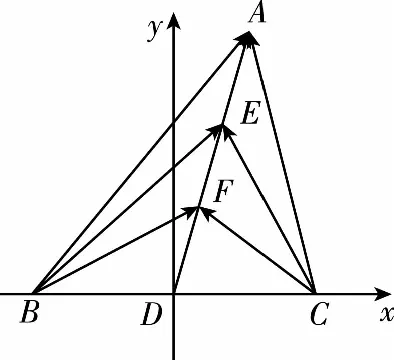
设B(-a,0),A(b,c),
因为D为BC的中点,所以C(a,0).
又因为E,F是AD上的两个三等分点,

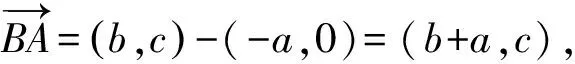
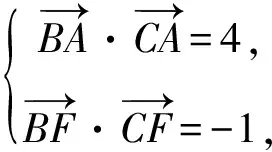
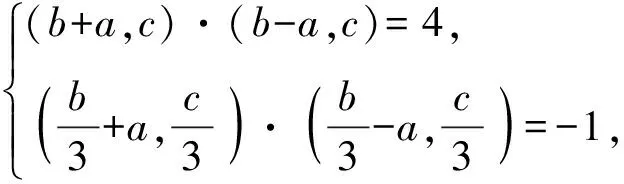


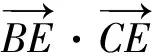
“极化恒等式”解法:因为D是BC的中点,所以由极化恒等式,


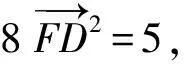
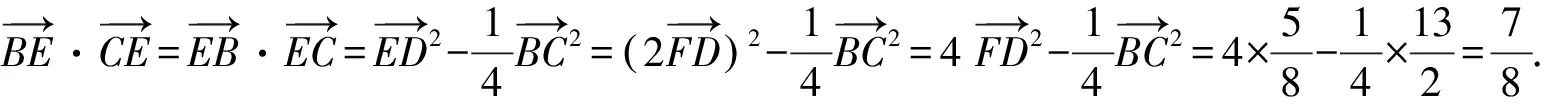
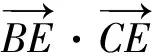
点评:两种常规解法无论是基底法还是坐标法,过程冗繁、复杂,计算量大,令人眼花缭乱,稍有不慎极易出错.而“极化恒等式”解法依据D是BC的中点,利用“极化恒等式”转化求解,则简捷、从容.常规解法与“极化恒等式”解法比较,孰繁孰简、一目了然,足以体现出“极化恒等式”的明显优势.
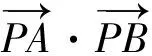
( )
A.[-5,3] B.[-3,5]
C.[-6,4] D.[-4,6]
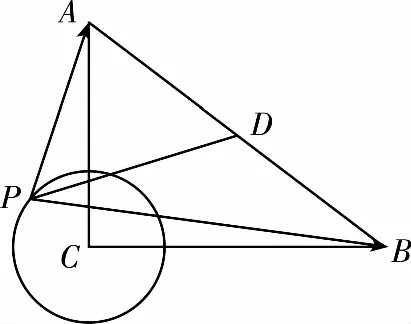
常规解法1.(坐标+三角)依题意建立如图所示的平面直角坐标系,则C(0,0),A(3,0),B(0,4),
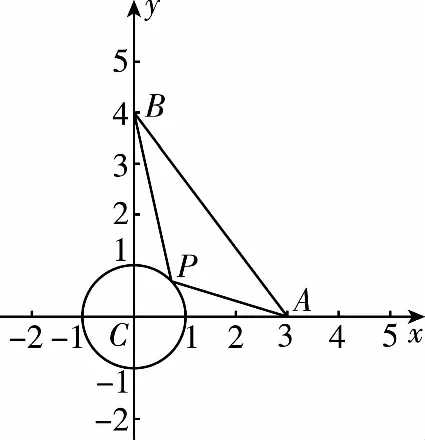
因为PC=1,所以P是以C为圆心,1为半径的圆上的动点,
设P(cosθ,sinθ),θ∈[0,2π],
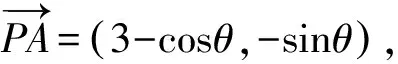

因为-1≤sin(θ+φ)≤1,
所以-4≤1-5sin(θ+φ)≤6,

常规解法2.(向量分解+三角)

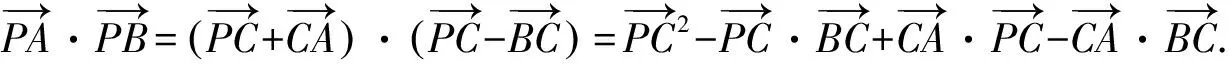
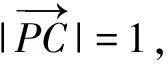



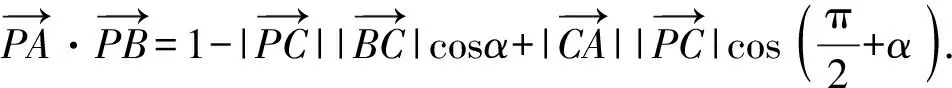
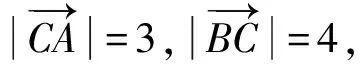

因为-1≤sin(α+β)≤1,
所以-4≤1-5sin(α+β)≤6,

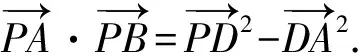
因为在Rt△ABC中,AC=3,BC=4,
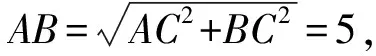

因为PC=1,所以P是以C为圆心,1为半径的圆上的动点,







四、结语

