问题启发 自然生成

李晓庆

［摘  要］ 启发式教学在发展学生数学思维、启发学生思考、激发学生数学灵感、提升学生学习能力等方面具有得天独厚的优势. 在教学中，教师应认真研究教材、研究学生，基于“三个理解”精心设计问题，让学生在问题的驅动下学会分析、学会探索、学会交流，学会用数学思维去思考并解决问题，以此提升学生的学习能力，落实核心素养.

［关键词］ 启发式教学；数学教学；数学思维；思考

数学是一门科学，也是一门文化，更是一门艺术. 若想将这门艺术演绎得淋漓尽致，教师需要将教学天赋、教学技能、教学技巧、教学经验、兴趣、心向等要素融于一体，并结合具体情境、学情将数学知识以简洁、精炼、明快的语言表达出来，从而让学生有所感悟、有所思考、有所发展. 好的教学不应当是简单的知识传授，而应该可以启迪学生思维，激发学生兴趣，拓宽学生视野. 为了实现这一教学目标，教师应启发学生去思考、去探索、去实践，从而在思考中学会发现，在探索中学会分析，在实践中学会创造，为此启发式教学应运而生. 如何在问题的驱动下启迪学生思维，让学生学会学习、学会思考呢？笔者以“弧度制”概念教学为例，谈几点对启发式教学的认识，现与同行交流，若有不足，请指正.

认识启发式教学

在启发式教学中，教师通过研究教材、研究学生、研究教学，寻求学生最容易接受的心理线索，并设计一些与之对应的数学问题来启发学生思考，诱发学生深度学习. 除此之外，教师要为学生提供一个平等的、和谐的教学氛围，鼓励学生带着问题进行探究性活动，以此提升学生与课堂的黏合度，激发学生潜能，让学生的“学”变得更加积极、主动. 当然，问题设计得好坏直接影响着课堂的参与度和思维的深度，好的问题能够快速地让学生进入学习状态，激发学生探究的热情，从而让学生动起来，课堂活起来，知识生长起来. 可见，启发式教学实施的关键在于数学提问，教师在问题的设计上应注意以下几点：

首先，问题要有方向性. 设计问题时应以教学目标为导向，将教学目标具体化，并设计出与之对应的数学问题，从而避免教学目标发生偏移，影响教学效果.

其次，问题要有启发性. 教师要从启发学生的角度提出问题，让学生自然地融入课堂教学中来，通过有效的分析，形成解决问题的策略. 若问题的设计上缺乏启发性，只是单纯地为问题而设计问题，将难以有效拓展学生的思维，不利于实现“教”与“学”的可持续发展，不利于培养学生的创新意识.

最后，问题要有层次性. 问题设计要体现思维的逻辑性，通过由浅入深的方式来激发学生参与的热情，提升教学有效性. 同时，教学中要尊重学生的差异，借助层次性问题让不同的学生都能有所发展.

启发式教学的目的是通过数学提问引导学生独立思考、主动探索、合作探究，让学生在问题的启发和引导下学会用数学思维思考问题，以此激发学生学习数学的积极性，全面提升学生分析问题和解决问题的能力.

教学活动设计

提出问题、分析问题、解决问题可谓是数学研究的三部曲，一切科学研究都需要经历以上过程，数学学习亦是如此. 在数学教学中，教师要结合教学实际提出数学问题，以此让学生在问题的驱动下进行数学思考，从而达到启发式教学的目的. 值得注意的是，这里的数学问题不是简单的“为什么”“如何做”，而是触及数学本质的、本原性的，能够直指知识核心的，具有统领作用的问题. 因此，在实际教学中，教师应认真研究教学，运用数学被发现时的本真问题来诱发学生思考，使其认清问题本质，领悟学习真谛.

在“弧度制”教学中，笔者将教学内容设计成层次递进、环环相扣的“问题串”，以期在问题的驱动下，启发学生思考，学会自主学习.

1. 以旧推新促生成

师：之前我们学习过直角三角形中的锐角三角函数，后面还要继续学习三角函数，请大家回忆一下，在初中阶段，我们主要学习了哪些内容呢？

生1：主要学习了正弦、余弦函数和正切、余切函数. 研究了一些特殊角（如30°，45°，60°等）的三角函数值.

师：很好，那你们还记得是根据什么来定义它们为函数的吗？

生2：根据函数的定义. 对于每一个确定的角A，都有唯一确定的sinA与之对应，所以sinA是A的函数.

师：很好，这体现了一个量随着另外一个量变化而变化的关系，可见三角函数定义符合初中的函数定义. 高中阶段对函数的概念进行了扩充，从映射的角度定义了函数，那么三角函数是否可以依据高中对函数的定义而重新定义呢？（生沉思）

师：回忆一下高中对函数的定义，你能从函数的概念中提炼出几个重要条件吗？（笔者放慢速度，让学生进行回忆、提炼）

生3：①两个非空的实数集A，B；②对于A中的任意一个数，在B中都有唯一的数与之对应；③对应关系“f”.

师：很好！表述清晰，提炼精准. 结合生3给出的三个条件我们来分析一下，初中对三角函数的定义是否也满足这三个条件呢？

师：现在我们以正弦函数为例，看看正弦函数在高中的函数定义下，是否依然是函数呢？（为了便于沟通和表述，笔者引导学生根据具体函数进行思考）

生4：正弦函数f（x）=sinx，x=30°，45°，60°，…，这里自变量x是有单位的量，不是“数”，不符合“A为非空的实数集”这一条件，所以在高中的函数定义下，它不是函数.

师：分析得很有道理，那么若想利用高中的函数定义继续研究下去，是否可行？有没有什么好的方法呢？

生5：根据刚才的分析我们知道，它只是不符合“实数集”这一条件，如果能够将“量”转化为“数”，是不是就可以继续研究了呢？

师：这个想法很不错，若能成功地实现这一转化，问题即可迎刃而解. 现在我们找到了解决问题的方向，具体应该如何转化呢？（生不语）

师：在初中我们是用什么来度量角的呢？

学生齐声答：角度制.

师：很好，谁来具体说一说？

生6：将一个圆周角记为360°，并把它360等分，每一等分角为周角的1/360，即1°的角.

师：表述得非常清晰，接下来如何将其转化成以“数”为单位的度量角的单位制呢？

生7：在角度制中把圓周角360等分，那么圆周长是否也可以360等分呢？如果可以是不是就完成转化了呢？

师：非常不错的想法，请大家按照这个思路继续思考，看看你得到了什么.

生8：把圆周长360等分，这样将1°角所对应的弧长l_o作为单位角. 已知圆周长为2πr，360等分后，得到的单位角为l_o=2πr/360=πr/180.

师：这样转化后，πr/180是否为“数”了呢？

生9：πr/180并不是一个数，因为其中含有r，所以πr/180应该为带有长度单位的量，不过这里的πr/180是一个实数.

师：分析得很有道理，看来πr/180是与r同单位的量，我们并没有成功地完成转化，如何将这个“量”转化成“数”呢？

生10：刚刚生9已经分析了，其中πr/180是一个实数，我们是否可以将πr/180中的r去掉呢？

生11：这个很简单，可以用l_o除以r，这样结果就没有单位了，也就是l_o/r=πr/180，这样就将量πr/180转化成了数πr/180，于是1°角的替换单位角为πr/180.

师：大家分析的思路是对的，实现了“量”与“数”的转化. 但是用πr/180作为单位角合适吗？是否可以把它变得更简洁一些呢？

师：思考一下，我们曾经学过的单位量，如长度、重量、体积等，其单位量通常是多少？

生12：这些单位量通常都是用“1”来表示的.

师：很好，无论从简洁的角度来分析，还是从运算的角度去思考，记为“1”会更加简洁. 我们可以将πr/180转化为单位“1”的形式吗？

生13：我感觉可以. 由于单位角是用l_o/r来表示的，若弧长l_o与r相等，即取l_o=r，则l_o/r=1，单位角l_o/r就转化成“1”了，这样是不是就转化成我们想要的单位“1”的形式了呢？

师：很好，经过大家的不懈努力，我们得到了自己想要的结果，先是完成了由“量”到“数”的转化，接着得到了想要的单位“1”的形式，其实这个就是我们今天要学的内容，度量角的另一种单位制——弧度制. 根据以上分析，对比角度制的定义，你是否可以为弧度制下定义了呢？

经历以上过程，学生顺利总结归纳出了弧度制概念. 在教学中，由初中的三角函数的引入，通过回顾初高中对函数的定义，引发认知冲突，启发学生进行“量”“数”转化，从而找到解决问题的突破口. 另外，在已有的角度制定义的启发下，学生联想到用每一等分的弧长l_o作为单位角，由此在“问题链”的引导下完成了度量角的单位制的推广，达到了教学目标.

2. 新旧对比促发展

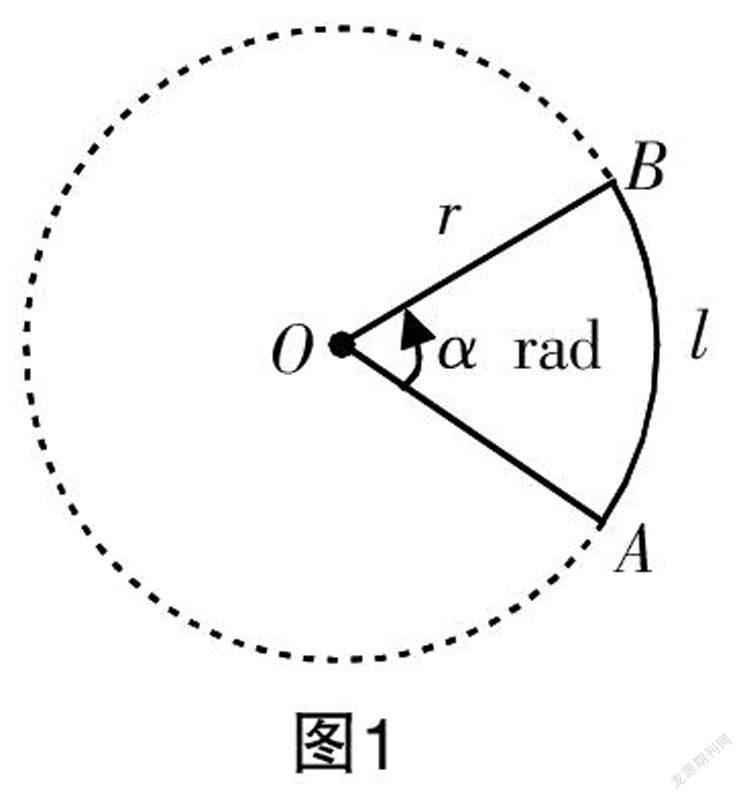
师：由此我们得到了弧度制的概念. 在弧度制中，规定弧度制单位用“rad”表示，读作“弧度”. 结合图1分析一下，弧度制下的角该如何表示呢？

生13：在半径为r的圆中，设弧长为l的弧所对的圆心角为α rad，那么α=l/r.

师：这个式子对于任意角通用吗？（笔者追问）

生13：哦！对的，α=l/r不能表示负角，那么是否可以用|α|=l/r来表示呢？这样就有正负之分了.

师：非常好！角有正角、负角、零角，那么在弧度制中，与之对应的弧度数就有正数、负数和0.

师：现在我还有一个疑问，某圆心角为α rad，它是数吗？

生13：α rad的单位为rad，是一个量，而α才是数，那么是否可以用α表示角呢？

师：很好的想法. 应用弧度制表示角时，通常是将rad省略不写的，只要写出角对应的弧度数即可，如角α=3就表示角α为3 rad，这样我们就可以用数来度量角了.

师：说一说，角的度量单位有哪几种呢？

学生齐声答：角度制、弧度制.

师：很好，以前我们学习长度、重量、面积等的单位时接触过单位换算，既然角度制和弧度制都是角的度量单位，它们之间是否可以换算？如何换算呢？（笔者鼓励学生合作探究）

生14：由|α|=l/r可知，圆周的弧度是2π，角度是360°，也就是说360°=2π，180°=π.

师：很好，借助圆周发现了它们的等量关系. 请将30°，45°，60°转化成弧度.

完成角度向弧度的转化后，笔者又给出了弧度，让学生将其转化为角度，由此通过角度与弧度的互化，使学生进一步理解角度和弧度的换算公式.

师：现在我们回到最开始的问题，此时是否可以将三角函数放到高中所学的函数概念中进行研究了呢？

学生齐声答：可以.

由此，在弧度制下，在角的集合与实数集R之间建立起了一一对应的关系，使之满足了第一个条件，剩下的问题也就迎刃可解了. 在本节课教学中，没有强制的灌输，而是通过一系列问题的启发，让学生主动参与概念的形成和发展过程，学生通过思考、探索、交流，最终达到了数学学习的目的.

教学思考

在弧度制概念教学中，笔者结合教材内容和学生实际，通过创设认知冲突启发学生思考，经历弧度制概念发现、形成和发展的过程，让学生亲身体验引入弧度制的合理性和必要性，让学生学会用数学思维思考问题. 同时，通过合理的问题启发，不仅激发了学生数学学习兴趣，而且培养了学生良好的数学素养，促进了学生学习能力的提升.

启发式教学贯彻“以生为主”的教学理念，关注学生数学核心素养的落实. 数学知识犹如一个“百宝箱”，其中既有知识、技能、方法，还有人的情感和价值观. 知识、技能、方法这些关于客观事物特性和规律的内容可以靠教师讲授完成，但是主观上的思想、情感、价值观等内容是需要学生在参与的过程中慢慢领悟的. 因此，教学中教师要为学生创造一些机会去经历、去体验，以此丰富学生的活动经验，逐渐完善个体认知结构，落实数学核心素养. 例如，在弧度制概念教学中，笔者通过对教材和学情的分析，将新旧知识进行对比、串联，设计了一条最适合学生发展、最体现知识本真的“问题链”启发学生主动思考、探索、交流. 学生不仅总结归纳出了定义，而且完成了角度制和弧度制的换算，解决了在高中的函数定义下继续研究三角函数的问题. 教学过程自然流畅，既实现了教学目标，又启发了学生，发展了学生，提升了教学有效性.

总之，在数学教学中，教师既要有渊博的知识、智慧的头脑，还要具备大胆的开拓精神. 在数学教学中，既要认真研究教材，又不拘泥于教材，要学会用数学问题来驱动教学，激发情感、启迪智慧，从而让学生会学、爱学.