初中数学实验教学运用策略

江苏省苏州市吴中区迎春中学

沈 萍

数学活动经验的积累是提高学生数学素养的重要标志.学生数学活动经验的积累是学生不断经历、体验各种数学活动过程的结果.数学活动经验需要在“做”的过程和“思考”的过程中积淀，是在数学学习活动过程中逐步积累的[1].而在数学教学中有效地运用数学实验，有助于积累数学活动经验，启迪学生思维，促进学生深度学习.

1 运用“联想—归纳”策略探索规律，培养学生规律意识

数学实验是一种有效的数学学习活动，它能够使知识内容变得形象具体化.数学实验的直观性，有助于激活学生对数学的学习主动性，并从动手操作、经历体验中发现数学的本质，探索规律，归纳总结，有助于培养学生主动发现规律的意识，促进学生数学思维的形成.

案例1在探索“正方体表面展开图”时，笔者引导学生动手操作，得到不同的正方体表面展开图，并总结正方体的表面展开图的口诀.

操作：

(1)课前分好小组，并让每位学生准备好一个正方体；

(2)课上请同学们沿着棱剪开，得到正方体的表面展开图.请组长将不同的正方体表面展开图展示在黑板上.

正方体的表面展开图共有11种，那么如何记住并判别正方体的表面展开图呢？笔者引导学生探索规律，归纳总结了正方体表面展开图的类型，并根据同一类型不同展开图的特点创新了通俗易记的口诀.

“141型”(如图1)口诀：中间四个一随意.

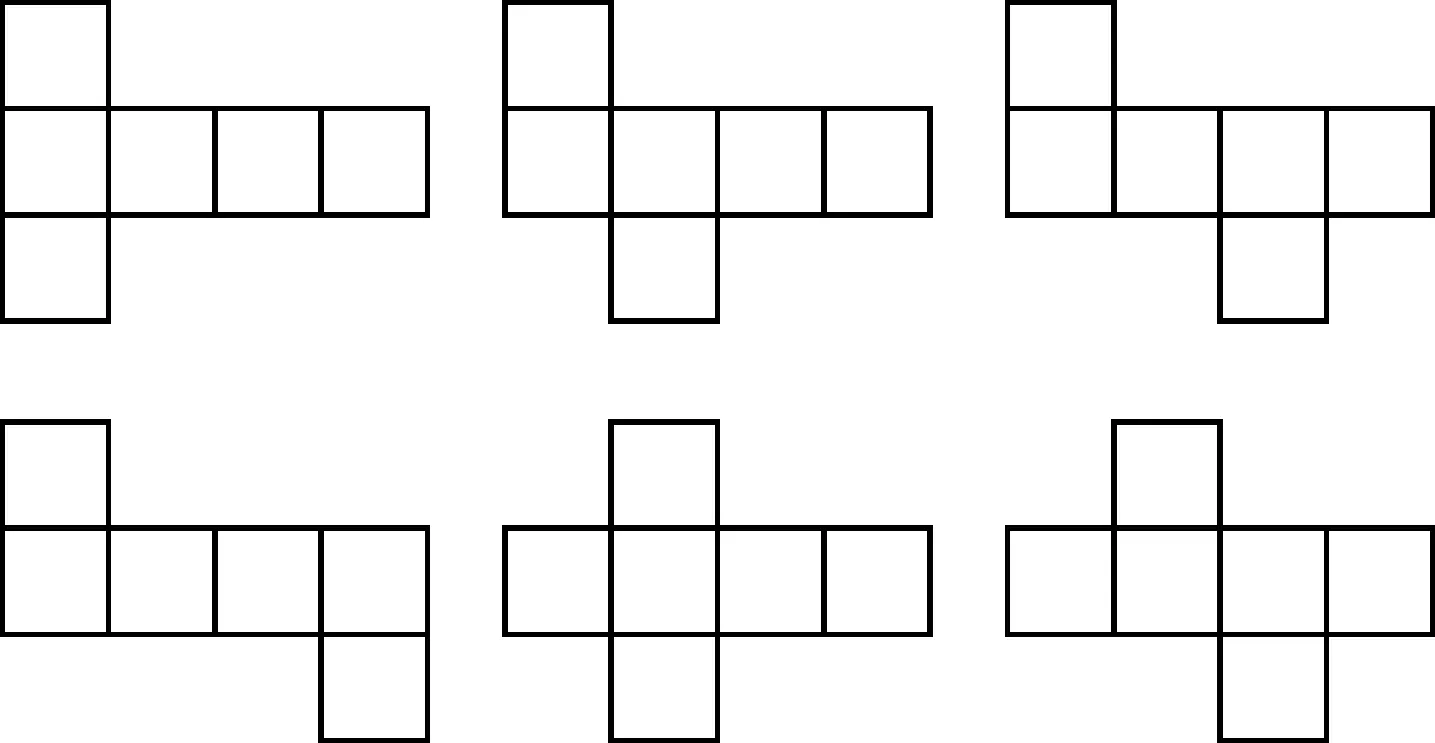
图1

“231型”(如图2)口诀：二三错开一随意.

图2

“222型”(如图3)口诀：两两相连各错一.

图3

图4

“33型”(如图4)口诀：三三两排错两位.

本案例由于是学生自己动手操作并探索出的规律，所以记忆会更加深刻.让学生主动参与数学实验，不仅能够激发学生浓厚的学习兴趣，有效促进数学实践能力的发展，促使学生思维与创造共生，实现课堂教学效益的最大化，还能无形中促进学生发生深度学习行为，发展学生思考探究的品质，培养学生的创新能力.

2 运用“猜想—验证”策略进行探究，培养学生探究能力

在数学课堂教学中，教师应充分发挥学生的主观能动性，运用数学实验，引导学生动手操作，让学生在操作中思考，提出猜想并进行有效验证，从而完成推理，获得最终结论.运用实验可以开发学生思维潜能，促进学生深入学习.

案例2在探索“同弧所对圆周角和圆心角的关系”时，笔者从学生的角度展开教学，巧妙地引导学生开展数学实验，进行动手操作.通过度量，猜想同弧所对圆周角和圆心角的关系.

操作1：学生用量角器度量，探究同弧所对圆周角和圆心角关系.

作法：

(1)要求学生在纸上画⊙O，并在圆上任取两点B，C；

(2)画出同弧BC所对的圆周角∠BAC和圆心角∠BOC；

(3)度量圆周角∠BAC和圆心角∠BOC.

猜想：圆周角的度数等于它所对弧上的圆心角度数的一半.

操作2：运用几何画板度量(更精确)，验证猜想.

让学生拖动点C，使圆心角∠BOC和圆周角∠BAC度数发生变化，观察几何画板度量出来的圆周角∠BAC和圆心角∠BOC的大小，发现圆周角∠BAC的度数始终等于圆心角∠BOC度数的一半(如图5).

图5

师：既然我们通过度量，发现了圆周角的度数等于它所对弧上的圆心角度数的一半.那么如何证明这个结论？我们先研究圆周角与圆心角具有特殊位置关系(即圆心在圆周角的一边上)的情形.

生：如图6，

∵OA=OB，

∴∠A=∠B.

∴∠BOC=∠A+∠B=2∠A.

师：圆心可以在圆周角一边上，还可以在圆周角的哪里？

生：可以在圆周角的内部或外部.

师：对于圆心在圆周角内部的情形，你能证明此结论吗？(可以转化为图6的情形)

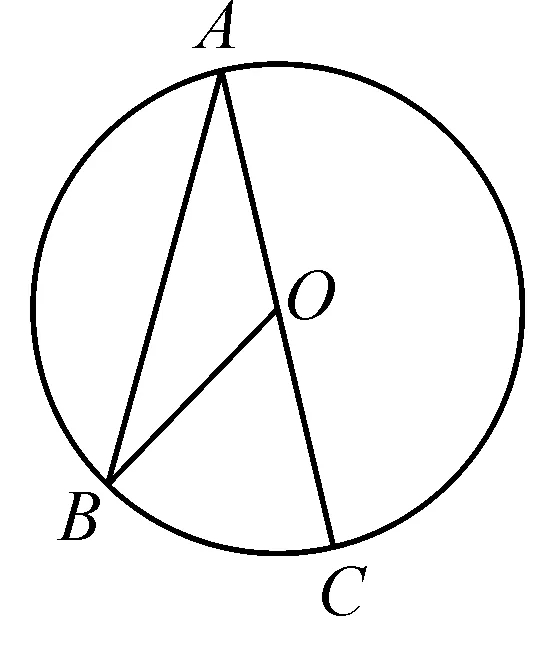
图6

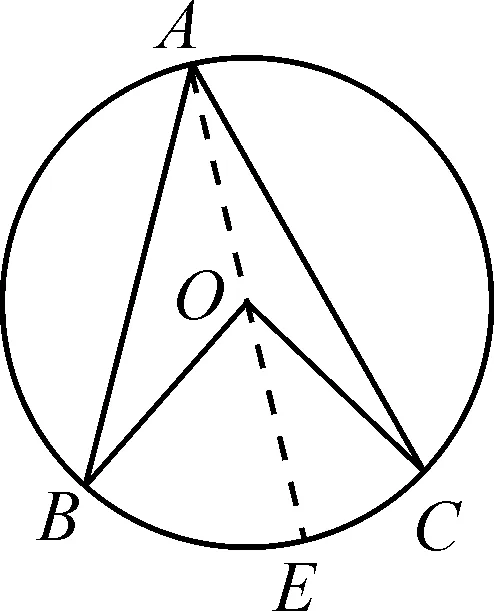
图7

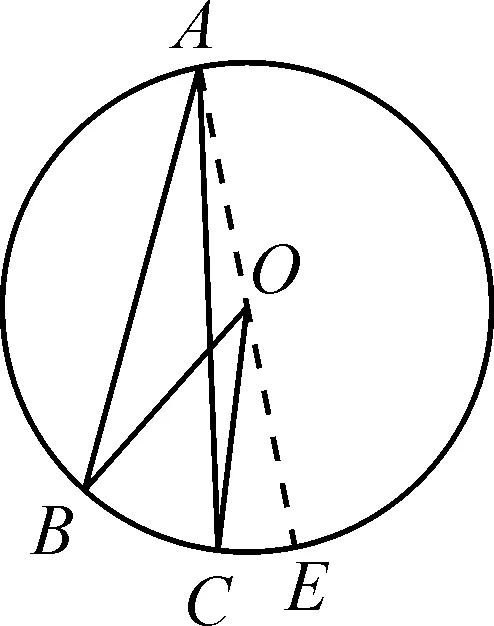
图8

生：如图7，当圆心在圆周角内部时，作直径AE，圆周角∠BAC就分成了两个圆周角∠EAB和∠EAC，且圆心O在边AE上.

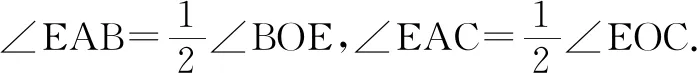
∵∠BAC=∠EAB+∠EAC，

师：对于圆心在圆周角外部的情形(如图8)，你能证明此结论吗？

此案例运用数学实验，让学生通过量角器度量得到猜想，运用几何画板进行验证，最后运用演绎推理证明，并渗透转化思想，使学生的学习热情达到高潮.在数学实验的情境下，引导学生自主探究，实现数学思想和实践的对接，激起归纳与演绎的融合，有效促进学生透过表象认识数学本质，从而提升学生学习深度，培养学生主动探究的能力.

3 运用“情境—模拟”策略动态模拟，突破教学难点

数学知识抽象且枯燥，学生解题时，常常会陷入难以理解的困境中，从而影响学生学习的积极性.因此为了帮助学生攻克难点，教师可以运用几何画板辅助实验教学，构建直观动态的教学情境，帮助学生对数学知识有更好的了解，从而突破难点.

比如，初中数学中的动点问题是中考的热点，也是难点，是学生比较头疼的问题.解决这类问题的关键是跟踪全过程，动中找静，变中找不变.但是由于数学知识的抽象，学生在分析时往往不够全面.若用几何画板开展数学实验教学，则可将动态变化的全过程直观地展示在学生面前，有助于学生分析和解决问题，从而攻克难点.

案例3在讲解“动点问题”时，笔者运用几何画板开展数学实验教学，分解难点.

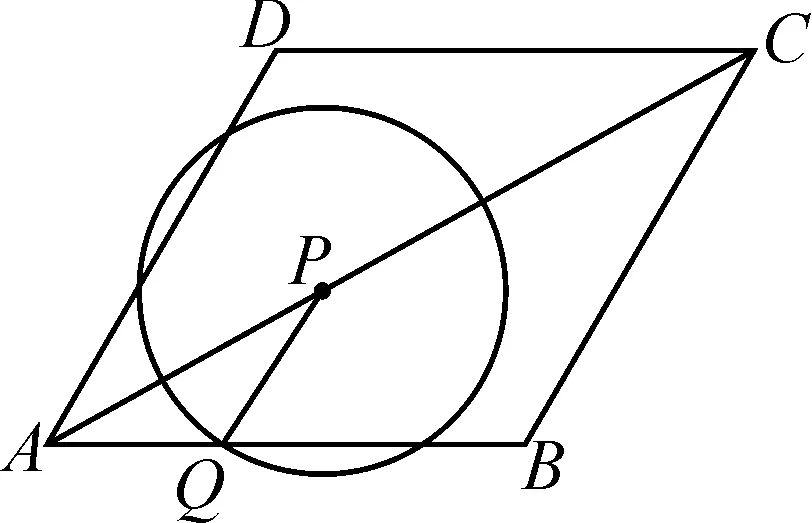
图9

(1)当P异于A，C时，请说明PQ∥BC；

(2)以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？

对于第(2)小题，⊙P与边BC分别有1个公共点和2个公共点的情形，学生往往分析得不完整，因此笔者运用几何画板展开数学实验教学，向学生展示⊙P运动的全过程，并要求学生观察⊙P与边BC的公共点个数的变化情况.

拖拉点P，点P从点A到点C的过程中，过点P作PH⊥BC于点H.如图10，⊙P与边BC没有公共点；如图11，⊙P与边BC有1个公共点；如图12，⊙P与边BC有2个公共点；如图13，⊙P与边BC有1个公共点；如图14，⊙P与边BC没有公共点；如图15，⊙P与边BC有1个公共点.

图10

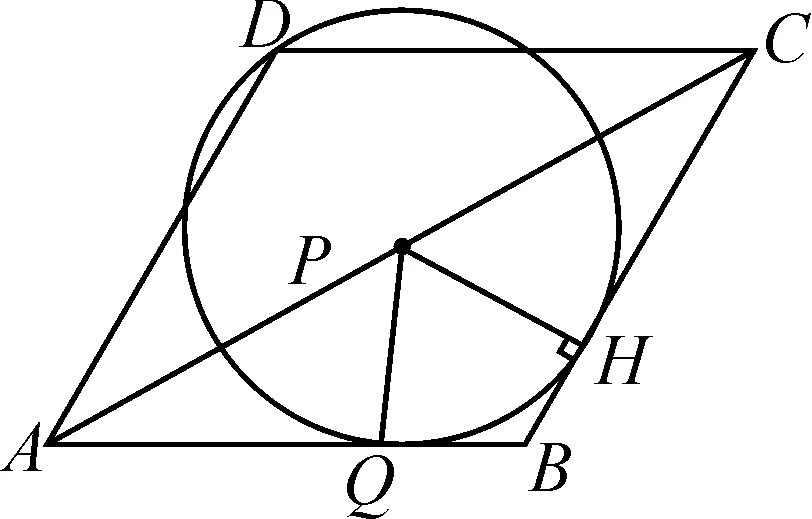
图11

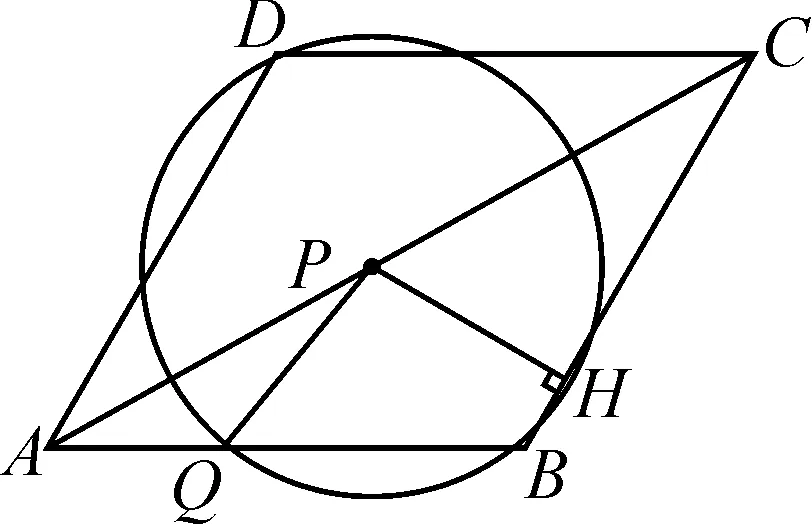
图12

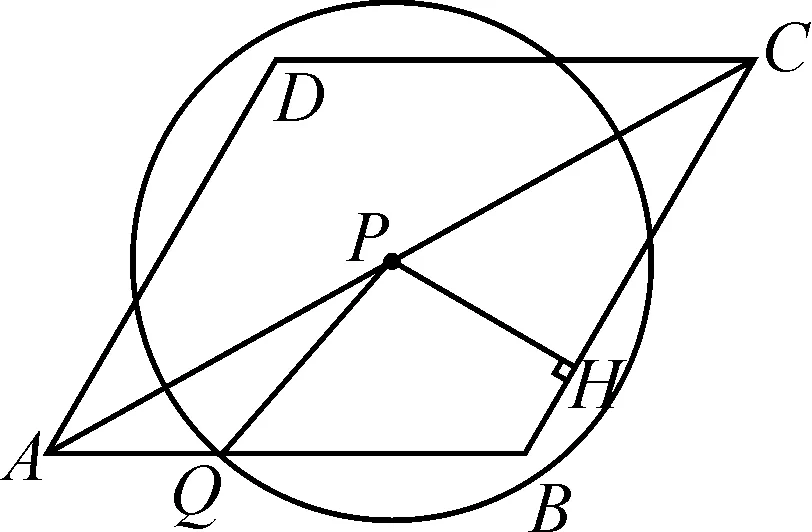
图13

图14

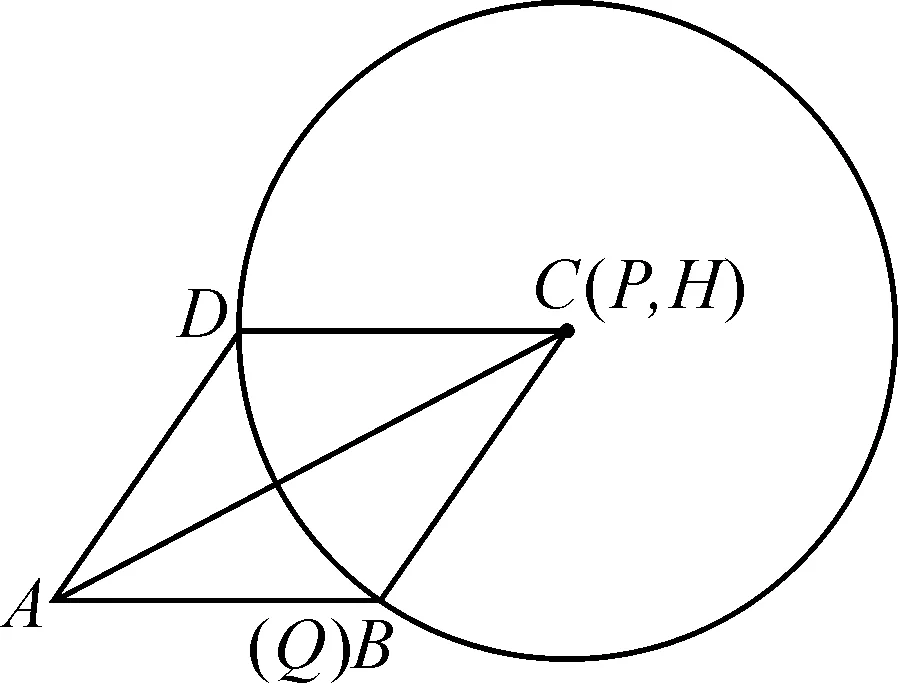
图15

为了解决t为怎样的值时，⊙P与边BC有1个公共点和2个公共点，教师可引导学生找到临界状态并计算t值.

在学生充分理解整个变化过程的基础上，笔者可以继续追问：“t取怎样的值时，⊙P与边BC无公共点？”

通过几何画板开展数学实验，可以攻克难点，引领学生探索数学知识的本质.不仅能有效地锻炼学生学习数学的思维方式，还能够加强学生分析和解决问题的能力，激发学生主动探索数学知识的热情，促进学习质量的提高.

4 运用“点拨—拓展”策略变换图形，培养学生洞察能力

图形的运动变换是初中数学的重要内容.运用实验，让图形动起来能揭示研究对象的本质.充分利用运动变换观察、认知、理解图形有助于学生几何直观能力的培养.

案例4在研究“圆的旋转不变性”时，笔者设计实验，让学生对透明纸片进行旋转，从而验证圆的旋转不变性.

操作：准备3张透明纸片(如图16-1,16-2,16-3).

①画⊙E，且与图16-1中的⊙O等圆，画∠CED=∠AOB.将透明纸片覆盖在⊙E上，圆心重叠，并用针尖固定圆心.旋转透明纸片.将透明纸片上的∠AOB旋转到∠CED的位置，你有什么发现？

②画⊙E，且与图16-2中的⊙O等圆，画CD=AB.同样按照上述方法操作，你有什么发现？

③画⊙E，且与图16-3中的⊙O等圆，画弧CD=弧AB.同样按照上述方法操作，你有什么发现？

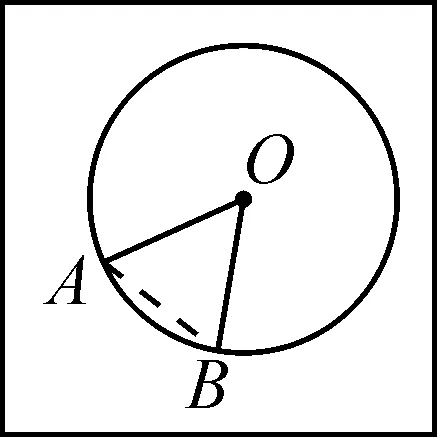
图16-1

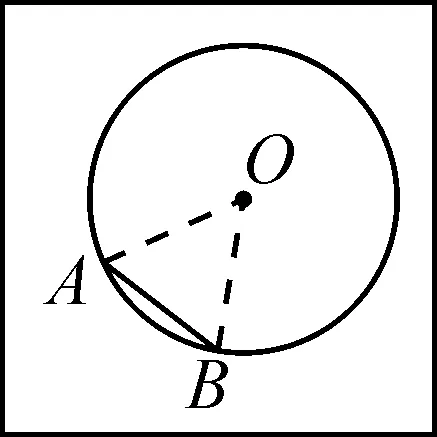
图16-2

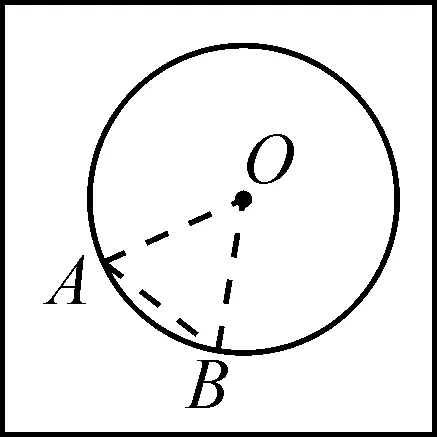
图16-3

此案例让学生经历图形旋转的运动过程，直观感受圆的旋转不变性，探究并验证在同圆或等圆中，圆心角、弧、弦的关系.运用实验，变动图形，让学生用运动的观念看问题，化静为动，动中观静，动静结合，发展了学生的动态表现力和直观洞察力[2]，有助于学生几何直观能力的培养，促进学生深度学习.

在初中数学几何与图形领域教学中，恰当地引入数学实验是引导学生发现问题、提出猜想、验证猜想和创造性地解决问题的有效途径.数学实验教学能调动学生各方面的学习经验，理清数学本质，深刻理解数学内涵，促进数学的深度学习，也有助于学生在数学思想感悟和理性精神培育上获得发展.