类比法在分式习题中的应用

2023-04-15南京市浦口区第三中学

中学数学 2023年4期

南京市浦口区第三中学

滕宏莲

在平时的教学中，经常会遇到一些较难的习题.若直接让学生做，学生往往一筹莫展，毫无思路；而若是教师单个逐题讲解，虽然学生当时掌握了，但由于是靠记忆去模仿，缺少了主动理解，过一段时间会很容易忘记.难题往往思维逻辑性强，考查的知识点多.而通过类比来讲解，类比知识间的前后联系和区别，将新学习的知识内化到原有的知识结构之中，找到新旧知识的连接点，就能够使知识顺其自然地呈现出来.这样不仅可以减少教师的讲解，还能增加学生的主动学习、主动思考，学生的记忆也会更加深刻.这样由被动学习转化为主动学习，可以大大提高课堂效率，这也是实现高效课堂的一种途径.

在数学的学习中，怎样运用对比和类比呢？简单地说就是对比两者的不同，类比两者的相同，通过归纳，获得有关问题的结论或者解决问题的方法.类比时要注意两者的不同，对比时要注意两者的相同.

1 运用类比法解决分式方程的增根和无解问题

分式方程中的增根问题、无解问题、解为正数(或非负数等)都是计算中的难点.如果就题论题，孤立地求解，学生学起来会非常困难.教师若能够运用对比和类比法，知识的讲授会更加自然.同时，能够减少教师的讲解，在教师的引导下，学生能够独立自主地解决问题.

1.1 运用类比和对比解决增根问题

若直接把这个题拿出来让学生做，大部分学生会无从入手.例1有两个难点，第1个难点是学生不知道方程有增根这句话如何用，第2个难点是因为有两个未知数x和a，不知如何解.

针对这个问题，教师先让学生解一个有增根的方程.

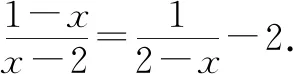
解：方程两边同乘x-2，得1-x=-1-2(x-2)，解得x=2.

把x=2代入x-2中，得x-2=0，所以x=2是分式方程的增根，故方程无解.

这个题目是将例1中的a变为数字1，求出x=2是方程的增根，分式方程无解.通过这个题让学生感受增根是怎样产生的.增根是由于解出来的x使分式方程中的分母为0,使得分式没有意义而产生的.

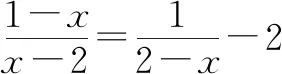
例1解题过程如下：

解：方程两边同乘x-2,得1-x=-a-2(x-2)，解得x=-a+3.

因为方程有增根，且增根为x=2，所以-a+3=2，求得a=1.

1.2 运用对比和类比解决无解问题

初中阶段学习的分式方程皆可转化为一元一次方程，转化为一元二次方程或其他方程的情况不在初中阶段的学习范围内.在此前提下，若分式方程有增根，则分式方程无解.但反过来并不成立，无解并不意味着分式方程只有增根，增根是无解的一种情况.但是要让学生理解这一点并不容易.教学时，若让学生将这两种题型进行对比，从中发现两者的不同，无解与增根问题就会迎刃而解.

学生出现的问题是把无解等同于有增根.很多习题也确实属于无解等同于有增根的情况.平时练习册中的习题一般是先易后难，比较简单的题目中方程无解就是方程有增根，所以学生先入为主认为方程无解和方程有增根是同一种情况.当遇到不止增根这种情况的习题时，出错率自然大大提高.

熟练地掌握无解不等同于有增根是解题的关键，我们可以类比例1解例2，可将例2与例1作对比，引导学生发现不同，主动寻找例2的问题所在，从而解决问题.

例2的解题过程如下：

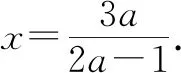
2 运用类比法解答分式的加减运算

我们知道“分式与分式方程”这一章可以类比分数来学习，其中分式有意义可以类比分数的分母不能为零，分式的基本运算可类比分数的基本运算，等等.但这一章最难莫过于“分式的加减”中异分母的加减.突破分式异分母的运算，还是要类比分数的运算.

异分母的计算最终都要转化为同分母的计算，找最简公分母是解题的关键，也是学生最容易出错的地方.在平时教学中，结合课本例题以及练习题，笔者将异分母加减的习题进行了归类，归为四类：一类是分母之间无公因式；二类是分母之间为倍数；三类是分母之间不是倍数关系，但有公因式；四类是整式与分式加减.这四类习题由易到难，学生更易掌握.下面通过四个例题来讲述这四类题型.

例4、例5和例6的学习同样都是类比分数的运算，以问题为导向，引导学生主动主动探究，并总结这类题的运算方法.

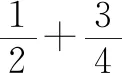
简单的一个分类，就能使学生类比分数来学习分式，不仅有利于理解，更是提高了学生主动探究的能力.这些例题层层递进，由易到难，由浅入深，在不经意间就解决了异分母的加减这一难点.通过类比来解答问题，让学生的学习由被动接受变为了主动探究，课堂的效率大大提高.在平时的教学中，只要善于发现知识之间的联系与规律，多一些引导，少一些灌输，让学生真正成为课堂的主人，那么我们的课堂就更加高效.