老题再现,生成初中数学课堂新智慧

[摘  要] 数学试题千变万化，在习题训练的过程中不仅要做新题还要关注老题，熟悉的试题重新再做会有意想不到的新收获. 教学中关注老题重做，随着学习阶段的深入，知识融合程度的提高，老题重做会出现新的思路，解题方法也会多样化，可以拓宽学生的视野，提升学生的解题能力.

[关键词] 老题新做;解题方法;拓展思路

作者简介：秦晨熹（1997—），本科学历，中学二级教师，从事初中数学教学工作.

数学知识的应用体现在习题中，因此许多学生在学习数学时容易陷入“题海”战术，教师也常常不断地给学生新的习题进行训练，但是效果却与预想的相差甚远. 事实上，题目千变万化，新的习题层出不穷，这就需要教师引导学生从变化多端的习题中寻找考查点，发现命题意图，从原有的老题中探寻新的解题思路，真正提升学生运用知识的能力，发现数学的本质. 笔者将从教学实践中谈一谈如何进行老题新做，促使新的习题教学方式生成，供各位同行分析讨论.

老题再现，拓宽视野

学生在数学学习的过程中会接触到许多习题，不同的阶段会产生不同的思路，教师要尝试结合学情适当改编老题，使学生在老题重做的过程中生成新的智慧，拓宽视野. 初三中考复习时，笔者给学生提供了一道八年级习题的改编题——老题新做[1].

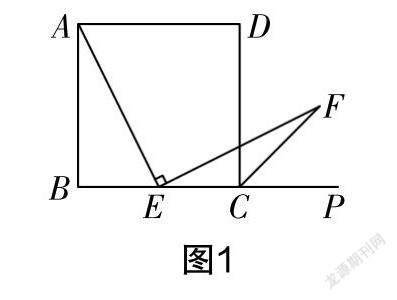
案例1  （1）在一次习题课上，王老师给同学们提出了以下问题：如图1所示，正方形ABCD的边BC上有中点E，∠AEF为直角，∠DCP的平分线为CF，与EF相交于点F. 求证：AE与EF相等.

经过思考，小华同学提出了一种正确的解答思路：取AB的中点M，连接ME，那么AM与EC相等，可以得到△AME与△ECF全等，因此AE与EF相等.

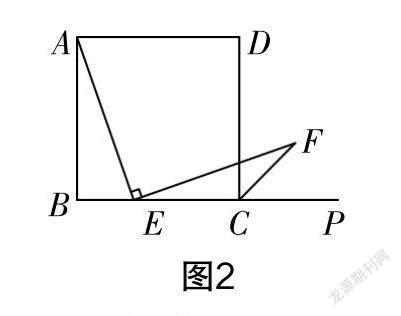
（2）在这一基础上，同学们进一步探究，有同学提出了其他看法. 小明提出：如图2所示，假设将“边BC上的中点E”改为“点E为BC边上除点B，C外的任意一点”，其他条件不变，那么AE与EF仍然相等. 请大家思考一下，小明提出的想法正确吗？你能不能说出理由？

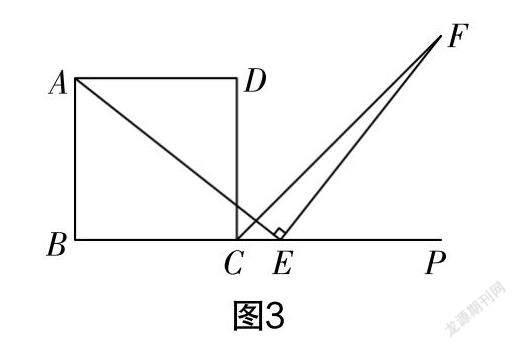
（3）小丽提出：如图3所示，边BC的延长线上有一点E是除C点外的任意一点，其他条件不变，那么AE与EF仍然相等. 你认为小丽的想法正确吗？你能不能说出理由？

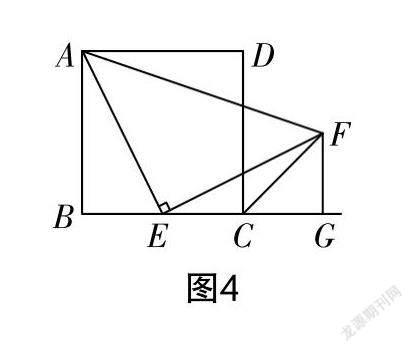
面对这样一道老题，讲解过程中笔者提出了一个常用的解法，即如图4所示，作FG垂直于BC，并与BC的延长线相交于点G，由此证明△ABE与△EGF全等. 在学习正方形时也做过这道题，当时这样添加辅助线是无法解决的.

生1：老师，我觉得这个方法现在可以证明了.

师：是吗？那你说一说你的想法.

生1：△ABE与△EGF相似，要进一步证明它们是全等的，只要证明它们的一条边相等就可以了.

（面对证明两条边相等，经过一番推理，仍然无法解决）

师：这个问题我们原来也研究过，但是这条路似乎走不通，不能这样构造全等三角形，但是从题目已知的条件来看这两个三角形应该是全等的，关键是如何进行证明.

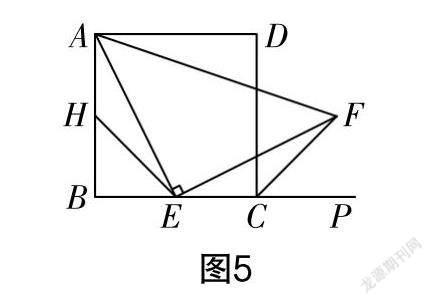
这样看来这道题要转换成证明三角形全等，如图5所示，取边AB的中点H，连接HE，可以证明△AHE和△ECF全等.

问题探讨到这里似乎已经可以结束了，这时突然有学生打断了教学.

生2：老师，前面的方法也可以证明三角形全等.

（生2刚才一直低头在思考，原来一直没有放弃前面的做法）

师：好的，那你说说怎么证明.

生2：如图4所示，通过△ABE与△EGF相似，可以证明==，因此EG是FG的两倍. 因为∠DCG被CF平分，所以∠FCG等于45°，所以CG与FG相等，EG等于CG的两倍，EG也等于EC的两倍. 因为BC的中点为E，所以BC是EC的两部，所以EG=BC=AB，于是△ABE与△EGF全等，可以得到AE与EF相等.

（生2的阐述使得学生都投来了欣赏的眼光，纷纷表示赞同，笔者抓住时机表扬了生2敢于质疑的创新精神以及积极思考的探究精神）

笔者继续问道：这个方法非常好，那么是不是后面的情况都适用呢？有兴趣的同学可以尝试一下.

学生在笔者的激励下，被点燃了学习的热情，教室里的学习气氛更加浓烈了，直到下课，学生还意犹未尽，一下课生2马上找到了笔者.

生2：老师，我用这种方法也能证明刚才题目中的第（2）问，只是较麻烦一点. 方法是这样的：如图6所示，过点F作FG与BC垂直，垂足为G，设FG与CG相等且都为x，BE等于y，EC等于z. 由第（1）问知道△ABE与△EGF相似，可得=，即=，所以x与y相等，即BE与FG相等. 又△ABE与△EGF相似，所以两个三角形全等，由此可以得到AE与EF相等.

这名学生的精神和想法也深深地影响到了笔者，驱使笔者也尝试用生2的方法去探究第（3）问，顺利地证明了点E在BC的延长线上的情况. 就是课堂上一个不经意的生成引发了一种新的解法，使学生的学习兴趣被激发了出来，产生了主动学习的热情，对数学充满了浓厚的学习兴趣，这将对其长期发展产生巨大的推动力.

学生的潜力是无限的，需要教师创设平等交流的氛围，提供有效的问题引导，在充分的思考空间和时间中激发学生巨大的潜力，实现新的发展. 学生多样的思维角度也会促进教师教学，为教学提供更加丰富的素材，使课堂教学更加精彩.

这一例题还可以通过圆的知识进行解决，方法更加简捷和巧妙，是一种新的思路，下面以点E为BC边上的任意一点为例进行介绍.

如图7所示，连接AC，AE，点E无论怎样移动，∠AEF都是90°，容易想到点E在直徑为AF的圆上，这样作一个辅助圆. 因为∠AEF与∠ACF相等且都是90°，所以点A，E，C，F四点都在同一个圆上，得到∠AFE和∠ACB相等且都是45°，所以△AEF是等腰直角三角形，所以AE=EF. 当点E在BC的延长线上也同样可以这样证明. 由此，大家可以得到一个结论：在一个动态变化的过程中，如果有一个角是不变的，就像这道题中的∠AEF，那么这个角的顶点（如本题中的点E）通常都会在一个圆上，这时将这个圆作出来，利用圆的知识就可以发现一种解题的途径. 可见，如果师生善于发现，一些看似和圆无关的问题，当能作出辅助圆时，便可以获得巧妙的解答方法.

变式练习以一题多变、一题多解的方式引导学生以更加丰富的角度看待问题，寻求更多的集体方法，学生能够充分调动思维活动，在体验、探究中发现数学，培养学生的发散思维. 在复习教学中注重老题新做可以通过一道习题涵盖更多的知识点. 通过一题多解的方式，培养学生思维的灵活性，当然也要注意具体情况的分析，思维灵活性仍然建立在夯实基础的情况下，要进行合理分配，才能全面发展.

老题再现指导命题

命题是教师需要具备的一项重要技能，只有研究命题才能在教学中更有针对性地对学生进行指导，提高学生的解题能力. 笔者受到生2的启发，将上述例题进行了改编，并呈现以下几道具有探究性的问题.

改编1：

（1）如图8所示，正方形ABCD的边BC上的中点为E，∠AEF为直角，∠DCG的平分线CF与EF相交于点F. 求证：AE与EF相等.

学生小刚提出了一种解题方法：过点F作FG与BC垂直，垂足为G，因为∠AEB与∠FEG的和是90°，∠AEB与∠BAE的和是90°，所以∠FEG与∠BAE相等. 又∠B与∠EGF都等于90°，所以△ABE与△EGF相似，因此==. 请你将后面的证明过程补充完整.

类比探究：

（2）在这个基础上，同学们进一步进行探究，小丽又提出了一个新想法：如图9所示，若将“边BC上的中点E”改为“点E为BC边上除点B，C外的任意一点”，其他条件不变，AE与EF仍然相等，而且可以用第（1）问中的方法进行证明，你觉得小丽的说法正确吗？你能不能说出理由？

拓展延伸：

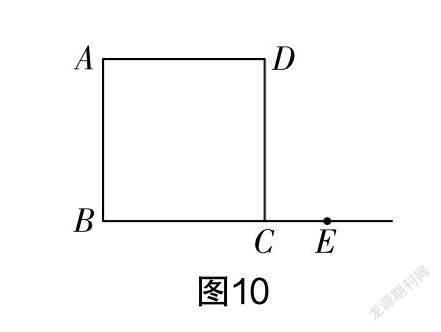
（3）边BC的延长线上有一点E是除C点外的任意一点，其他条件不变，那么AE与EF仍然相等吗？请你在图10中将图形补充完整，并进行证明，证明的方法不限.

中考题中几何探究题是必考点，主要考查学生图形的综合推理能力，涉及图形的移动、翻转、旋转、折叠等，经常需要通过添加辅助线实现图形转换. 笔者进行了上述试题的改编后，觉得还不够完善，毕竟在中考题中考查学生一种不经常使用的证明方法不是特别合适，大部分学生在考试中运用新的证明方法来解答的可能性是很小的，因此这道题目就失去了区分度，体现不出选拔的功能，但是对提升学生的思维能力还是非常有益的，可以作为课后的拓展和提优. 命制试题的过程是一个不断完善的过程，在教师的教研活动中，几位同行与笔者共同探讨了这道试题，再次进行了改编，更加贴近中考的要求. （改编后的试题如下）

改编2：

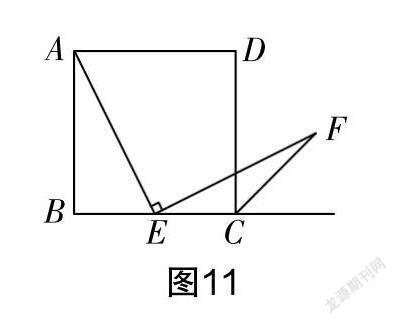
已知正方形ABCD的边BC射线上有一点E，点E不与点B重合，连接AE. 如图11所示，当点E是线段BC的中点时，将线段AE绕着点E顺时针旋转90°，得到线段EF，连接CF，发现∠FCB等于135°.

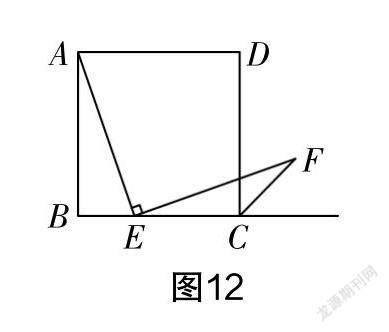
（1）如图12所示，当点E是线段BC上的任意一点时，将线段AE绕着点E顺时针旋转90°，得到线段EF，连接CF，∠FCB的度数会发生变化吗？请说明理由.

（2）如图13所示，当点E是线段BC延长线上的任意一点时，将线段AE绕着点E顺时针旋转90°，得到线段EF，连接CF，请你说一说线段AE，CF和CE之间的数量关系，写出你的结论和理由.

（3）假设BE等于AB，请你直接写出∠CFE的度数.

这道题经过这样的改编后变得更容易入手，解题方法更加多样化，可以通过不同的方法添加辅助线从而构造全等三角形，多种解题方法也符合中考题的考查特点，能够考查学生思维的灵活性和逻辑推理的能力. 第（2）问求证三条边间的数量关系，提高了难度，具有较强的区分度，也体现出了问题间层层递进的梯度，在注重基础知识考查的情况下，兼顾中考的选拔功能[2].

教学实践与反思

复习教学中通过老题新做和老题新编能够不断发掘试题蕴含的价值，能够充分调动学生运用知识从多个角度思考问题. 复习教学中的老题新做的价值不止于此，教学中还可以通过基础图形的不断丰富，构建知识系统，提升解题能力.

案例2  一般三角形.

（1）从图14的△ABC中，你发现了三角形的三条边和三个角之间有什么关系吗？请你说一说你判断的理由.

（2）从图14的△ABC中，猜想一下它的边之间与角之间的大小关系，并证明你的猜想.

案例3  特殊三角形.

等腰三角形：

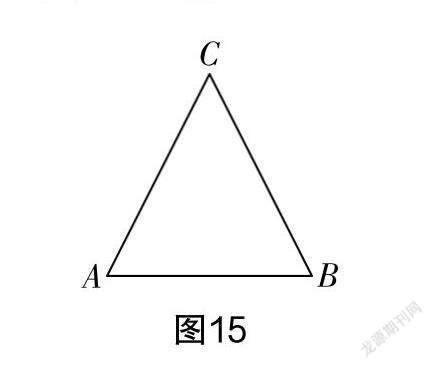
（3）在图14的基础上，假设CA与CB相等，△ABC就成了等腰三角形，那么图15中的等腰三角形ABC的边、角以及边和角之间有着什么关系呢？请你说一说你判断的理由.

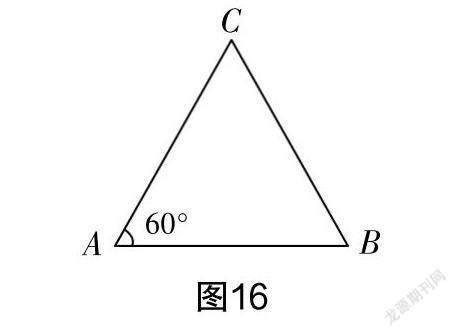
（4）在图15的基础上，若∠A等于60°，△ABC就成了等边三角形，如图16所示，请你仿照第（3）问，研究等边三角形的性质.

直角三角形：

（5）在图14的基础上，若∠C是直角，△ABC就成了直角三角形，如图17所示，请问直角三角形ABC的边之间和角之间有着什么数量关系呢？

（6）如图17所示的直角三角形ABC的边和角之间有着什么样的函数关系呢？

（7）在图17的基础上，若∠A等于30°，你又有什么新的发现呢？

以上这些都是学生非常熟悉的基本图形和基础题、老题，在复习过程中如何更好地利用它们进而发挥试题的功能呢？在该例中教师可将一个基本图形的边和角根据考查的知识点不断进行推理和演化，形成一个新的“图形链”，演绎思维由一般到特殊的进程，再通过“图形链”让学生进行专题复习，以实现更加系统化的复习，在老题新做中生成新的课堂智慧.

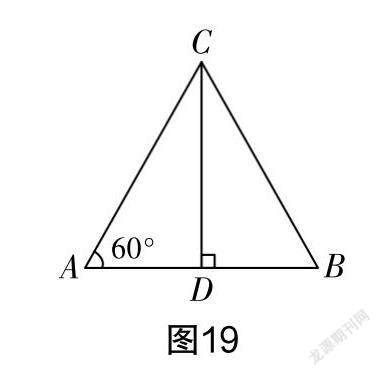
在教学的过程中教师还可以通过在基础图形上添加新的元素使基础图形更加丰富，呈现出多样的变化，引导学生产生新的结论，再通过证明结论获得新的发现. 从图16来说，如果添加条件“CD与AB垂直，垂足为D”，如图19所示，你会有什么新的发现呢？

在这些基础图形上教师还可以通过添加辅助线的办法使图形更加丰富，生成更多新的试题，发展学生的思维. 在进行老题改编前，教师要非常明确考查的知识点，用知识点来连接，以使知识更加系统化;同时要明确通过什么样的方式将知识呈现给学生，让学生学得更加有效. 在老题新做和老题改編的过程中，教师要引导学生不断深入交流和探讨，培养他们追求真理的科学精神，领悟数学的本质.

随着学生学习的知识不断积累，研究的方法更加丰富，在老题新做的过程中会出现新的思路和方法，使学生的解题能力不断提升，对于知识的理解更加深刻. 教学中教师要不断钻研，理清知识之间的联系，研究命题技术，不断突破传统思维，实现数学教学的新跨越.

参考文献：

[1]陈向明. 质的教育研究中研究问题的界定[J]. 教育评论，1999（01）：28-31.

[2]喻平. 数学学科核心素养要素析取的实证研究[J]. 数学教育学报，2016，25（06）：1-6.