四阶变系数Schrödinger方程的适定性与正则性
2023-04-11白忠玉
白忠玉
(海口经济学院 网络学院, 海口 571127)
常系数Schrödinger方程的适定正则性和能控性已有许多研究结果[1-3]。对于变系数Schrödinger方程,验证其适定正则性一直是一个困难的问题,要根据不同的方程形式采用不同的工具,过去的做法是把控制问题转化为不可验证的假设。十几年前引入的微分几何估计,是解决变系数Schrödinger方程控制问题的一个有力工具,从此在变系数Schrödinger方程的适定正则性及可控性方面取得了许多进展[4-7]。
为了给出要研究的方程,下面先定义几个算子。
令A(x)=[aij(x)]n×n是定义在Ω上的实对称矩阵,且对常数a,b>0,满足

(1)
P是一个二阶偏微分算子:
(2)
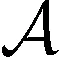
(3)
且
ν
(4)
其中ν=(ν1,ν2,…,νn)为∂Ω上指向Ω外部的单位外法向量。
A是L2(Ω)中的正定自共轭算子,定义为:

(5)
考虑如下变系数Schrödinger方程:

(6)
其中Ω⊂Rn(n≥2)是开的有界区域,具有C3光滑边界,∂Ω=Γ,u是边界控制,y是边界观测,算子P、、A分别由式(2)、(3)和(5)定义。
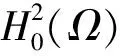
文献[5]证明了Schrödinger方程在Neumann边界控制下的适定性,而没有给出系统的正则性。目的是研究Dirichlet边界控制和同位观测的Schrödinger方程(6)的适定性与正则性,把文献[5]中研究适定性的方法推广到Dirichlet边界上,得出系统(6)的适定性,然后利用适定性结果,证明了系统(6)是正则的。
1 预备知识
令G(x)是正定矩阵,ρ(x)是其行列式,
ρ(x)=detG(x), ∀x∈Rn


(7)
则(Rn,g)成为带有度量g的Riemann流形[8]。
由式(1)、(4)和(7),得
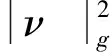
(8)


其中DXN表示向量场N关于X的协变导数。

其中: div0是欧式空间Rn上的散度算子,▽g、divg和Δg分别为流形(Rn,g)上的梯度算子、散度算子和Beltrami-Laplace算子。
下面给出一个乘子等式。

现在将系统(6)化为在状态空间H=H-2(Ω)中的一阶抽象系统。
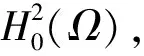

于是系统(6)能被改写为:

(9)
等同H和它的对偶H′,则有下列Gelfand三嵌入:
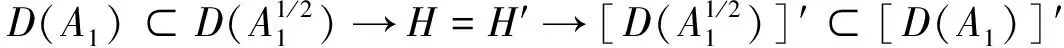


(10)


(11)

(12)




(13)
于是系统(6)化为一个在状态空间H中的一阶抽象系统:

(14)
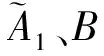
2 主要结果
第一个结果是系统(6)的适定性,是文献[5]中定理1.1的推广,表明系统(6)在状态空间H和输入输出空间U=Y中是适定的[14]。
定理1对∀T>0,u∈L2(0,T;U),系统(6)存在满足初值条件w(·,0)=w0∈H的唯一解w∈C(0,T;H)和不依赖于(w0,u)的常数CT>0,使得为证明定理1,需要下面的引理2。

引理2[15]若∃T>0,CT>0,使得当初值为零时,系统(6)的输入输出满足
则系统(6)是适定的。
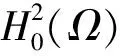
(15)
因此,定理1成立当且仅当对某一(从而对所有)T>0,存在常数CT>0,使得方程(15)的解满足
(16)
定理1的证明下面将分4步证明式(16)成立。

(17)
计算式(17)左边的第一项,有


(18)
由引理1,有
(19)
把式(19)代入式(18)中,得
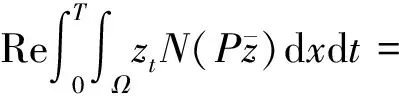

(20)
计算(17)左边的第二项,得


(21)
由式(17)、(20)和(21),得

(22)
其中






C(0,T;H-2(Ω)×L2(Ω))
(23)
u∈L2((0,T)×Γ)
(24)
于是,根据文献[5]中的引理2.4,有

(25)
第三步(估计R2) 为了估计R2,先把u限制在L2((0,T)×Γ)的具更高光滑性的稠密子集中:
u∈C2((0,T)×Γ),u(x,0)=u(x,T)=0
在R2中,对t进行分部积分,得


(26)
由式(24)和(26),得

(27)
第四步(估计b0,T) 由式(24),得

(28)
最后,从式(22)、(25)、(27)和(28),结合式(8),知式(16)成立。证毕。
第二个结果是系统(6)的正则性。
定理2系统(6)是正则的,并且其直接传输算子为零。确切地说,如果w(·,0)=wt(·,0)=0,且u(·,t)=u(·)∈U是一个阶跃输入,则相应的输出y满足
由于系统(6)是适定的,根据文献[18]的附录,系统(6)的传递函数为:
(29)
进而,由定理1宣称的适定性还意味着存在正常数M,α>0[17],使得
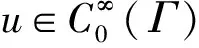
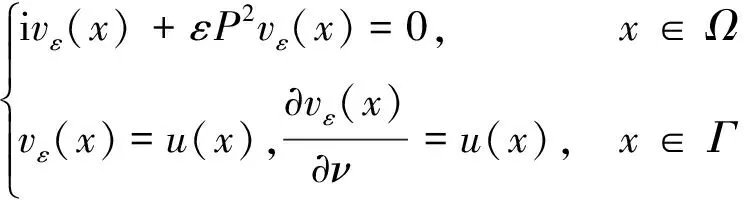
(30)
的解uε满足
(31)
则定理2成立。
证明只需证明在U的强拓扑下,H(λ)u沿着正实轴趋向于零[19],即对于任意的u∈L2(Γ)=U,有

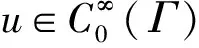
则vλ满足

(32)
和
(33)


的唯一解,则式(32)可化为:

或
-iλ
因此,式(33)就成为:
(34)
令vε(x)=vλ(x),即ε=λ-1,并取极限ε→0,则由式(34)知命题成立。
定理2的证明由命题1,只需证明式(31)。从式(30)的边值条件易得式(31)成立。证毕。
