特征降维的深度强化学习脑卒中分类预测研究
2023-04-11袁甜甜李凤莲张雪英胡风云贾文辉
袁甜甜,李凤莲,张雪英,胡风云,贾文辉
(1.太原理工大学 信息与计算机学院, 太原 030024; 2.山西省人民医院, 太原 030012)
脑卒中是严重威胁全球居民公共健康的疾病之一,是全球范围内致死、致残的重要原因[1]。脑卒中主要分为缺血性脑卒中和出血性脑卒中两大类,其中缺血性脑卒中约占脑卒中发病总数的70%。脑卒中的主要发病特点是发病急和病情发展迅速,大多数的患者得不到及时治疗。研究表明,约94%的脑卒中发病因素是可以提前干预的[2]。因此,预测个人脑卒中的发病风险尤为重要,且具有挑战性。
脑卒中发病风险预测涉及脑卒中发病风险影响因素的选择以及脑卒中发病风险预测模型构建两方面内容。其中影响因素的选择是从众多影响因素中筛选出最重要的发病危险因素或者挖掘出潜在未知的影响因素,以辅助指导临床医生进行发病前危险因素干预,降低脑卒中发病率。同时,选择合适的分类模型,进行模型构建及性能测试也是极为重要的。目前机器学习领域已经有多种成熟的分类模型,如决策树、SVM(support vector machines)、贝叶斯分类器以及集成分类器等。近年来,随着人工智能的发展,基于深度强化学习的分类模型也呈现较强优势,成为近年研究热点。深度强化学习融合了深度神经网络及强化学习二者优势,既具备强化学习强大的自主学习能力,也展现了深度神经网络较强的分类性能。本文主要从特征降维及构建预测模型2个角度,开展脑卒中发病风险预测研究。
在分类问题中,数据的高维度是面临的巨大挑战之一。消除数据的大量冗余特征,以获得较低的执行时间,并产生较好的分类性能,是有效提高分类器性能的一项措施。特征降维是去除冗余特征的有效方法,主要分为特征选择(feature selection,FS)、特征提取(feature extraction,FE)和混合式方法。特征提取是基于原始特征通过属性转换或者属性映射得到新的特征组合,主要包括主成分分析法(principal component analysis,PCA)[3]、线性判别分析法(linear discriminant analysis,LDA)[4]和独立成分分析法(independent component correlation algorithm,ICA)[5]等,缺陷是改变了原始特征的数据分布。特征选择方法采用选定的评价标准从原始特征中选取小部分特征作为原始特征的特征子集,以去除不相关、冗余特征[6],主要分为过滤式(filter)、封装式(wrapper)以及嵌入式(embedded)[7]3种,优势是不会改变原始特征的分布,但只是对原有特征的选择,存在一定的局限性。混合式方法可以聚合不同方法的特征子集来解决特征选择中的高维问题,提高所选特征的可信度与稳定性是近年的研究热点。Thomas等[8]提出一种高效的混合特征子集选择方法,采用基于相关性的过滤式方法选出特征子集,再使用封装式方法选出最终特征子集。江泽涛等[9]利用Fisher方法对特征进行降维,再引入Helly属性对得到的特征子集进行再次筛选,最后使用随机森林和改进的K-means作为联合分类器,选出最终特征子集。本文中提出一种混合式特征降维FS-FE方法,充分发挥了2种算法的优势,实现优势互补。
在脑卒中发病风险预测模型构建方面,近年来也有学者开展相关研究。随着人工智能在智能医疗领域研究的深入,基于机器学习理论进行脑卒中发病风险预测成为了研究热点。2013年,谷歌DeepMind团队将强化学习的决策能力与深度学习的感知能力有效结合起来,创新性地提出了深度强化学习(deep reinforcement learning,DRL)[10]。自从深度强化学习问世以来,不少学者将其应用于各种领域,且取得了不错的效果。闫军威等[11]采用具有双神经网络的Q-Learning算法解决了中央空调建模困难以及参数辨识复杂的问题。在脑卒中发病风险预测模型构建方面,田豆[12]开展了基于深度强化学习的脑卒中发病风险预测模型构建研究,该文献使用卡方检验去除数据集冗余特征,降低模型分类复杂度,选用了平方误差损失函数构造深度强化学习模型,结果表明其思路是可行的,但是具有运行时间较长,性能不够理想的缺陷。
为了取得更好的分类预测效果,本文采用双神经网络结构的Q-Learning学习算法(double Q-Learning)[13]和基于竞争构架Q-Learning(dueling DQN)[14]学习算法框架,建立深度强化学习分类预测模型。此外,提出了一种更具有鲁棒性的损失函数,以加快模型训练速度,并提高分类预测性能。最后,对所提出的模型在UCI数据集以及脑卒中筛查数据集进行实验验证,并与已有模型进行预测性能对比,结果表明所提模型是有效的。
1 混合式特征降维方法FS-FE
特征降维能够得到对分类预测模型更重要的特征子集或特征组合,取得更好的预测性能及更高的执行速度,广泛应用于分类预测领域。本文中提出了一种基于特征选择和特征提取的混合特征降维方法(feature selection and feature extraction,FS-FE),该方法可以降低数据维度,减少训练时间,并取得更好的分类效果。特征提取和特征选择方法都有各自的局限性,将两者进行结合,有助于充分发挥二者优势,扬长避短。
1.1 混合特征降维方法FS-FE实现机理
FS-FE特征降维方法的设计:首先,选用基于相关性的特征选择算法(correlation-based feature selection,CFS)[15],考虑到信息增益倾向于更多特征的特征子集,本文引入了最大信息系数对CFS算法进行改进。接着,选用了主成分分析法PCA,对过滤后的特征子集采用特征提取进行再次降维,从而得到最优特征组合。混合式特征降维方法如图1所示。

图1 混合特征降维方法
所提方法的实现过程:① 将数据集F采用改进的CFS进行特征选择,根据评价函数计算特征价值,利用最佳优先搜索方法,选出精简特征子集F1。② 将得到的特征子集F1选用PCA算法进行特征提取,得出最优特征组合F2。
1.2 改进的基于相关性的特征选择算法MCFS
CFS是一种基于特征搜索空间的过滤式特征选择方法,其主要思想是选出的特征子集与类别属性相关性高且与特征之间彼此相关性低。CFS采用信息增益求解属性间的相关性,易倾向于选择具有更多属性取值的特征。为此,提出一种改进的特征选择算法(MIC and correlation-based feature selection,MCFS),该算法采用最大信息系数(maximal information coefficient,MIC)[16]对特征与特征之间的关联性进行校正。这种改进思路不仅可以考虑特征之间的冗余度,也考虑了特征与类别之间的关联性。
MCFS算法对特征子集的分类能力评估,使用最佳优先搜索方法[17],其评价函数计算公式如式(1)所示:

(1)

(2)
式中:S、R分别是特征与类别;H(S)、H(R)分别是S、R的信息熵,采用式(3)求解;gain(S,R)为信息增益,采用式(4)(5)求解。对称不确定性SU越大,S、R之间相关性越高,表明该特征对类别影响越显著。

(3)
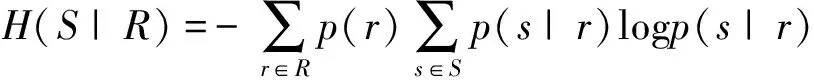
(4)
gain(S,R)=H(S)-H(S|R)
(5)
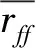
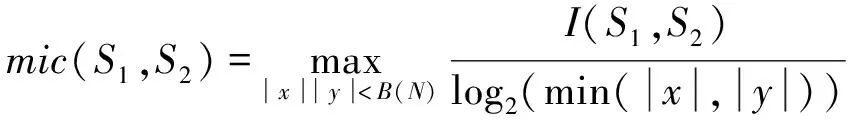
(6)
式中:I(S1,S2)是互信息,采用联合概率密度来计算。MIC指标将特征S1、S2之间的关系离散到二维散点图空间中,其中x、y是该二维散点图空间格子的划分数,N为样本数,B(N)是关于样本的函数,根据文献[19],取B(N)=N0.6。2个特征的MIC越小,相关性越低。
1.3 特征提取算法
主成分分析法(PCA)是一种无监督的特征提取算法,通过线性变换的方式将原始数据转换为一组维度线性不相关的特征空间,提取出原始数据的主要特征分量。PCA算法在特征降维的同时尽可能保留原始数据的重要信息,通过确定特征之间的相关性,确定数据集的主成分[4]。主成分分析法实际上是一种转换技术,使用更少的特征来表征原始数据集。
2 优化的深度强化学习分类预测模型NL-DQN
通过分析脑卒中分类预测问题的特点,建立分类预测问题对应的马尔可夫决策过程。结合双神经网络结构与决策网络模型的深度强化学习算法,解决值函数过估计以及智能体在不同状态下采用不同动作的问题。基于此建立了脑卒中发病风险预测的深度强化学习分类预测模型NL-DQN(new loss function deep Q network),该模型基于Double Dueling DQN构建,图2为Double Dueling DQN的原理框图。同时,对损失函数进行了改进,以提高模型性能。
2.1 马尔可夫决策过程
强化学习主要思想是智能体与环境不断交互学习,通过试错来获得知识,利用反馈信号来优化决策序列。强化学习的目的就是寻找最优的动作策略[11],以取得最大化的累计奖赏值。建立待分析问题对应的马尔可夫决策过程是应用强化学习的前提。
在本文中,把分类问题建模为顺序马尔可夫决策过程,智能体的动作空间是当前样本可能选择的预测类别。在分类正确时,智能体获得0的奖赏;当分类错误时,智能体获得-1的奖赏。奖赏函数如式(7)所示:

(7)
Q-Learning是一种基于价值的强化学习方法,通过寻求最优函数Q*,表示智能体在当前状态s下选择最优动作a,可获得最高的累计奖赏值,其动作-值函数映射关系满足贝尔曼方程,如式(8)所示:
Q*(s,a)=Eπ(rt+γQ(st+1,at+1)|st=s,at=a)
(8)
式中:γ∈(0,1)为折扣因子,当γ=0时,智能体只受即时奖赏值的影响,当γ=1时,智能体受即时奖赏与长期奖赏的影响是等价的。折扣因子反映了当前动作对奖赏值的影响。
最优策略π*(s,a)是在状态s下选择Q最大的动作,即贪婪策略,如式(9)所示:
π*(s,a)=arg maxaQ(s,a)
(9)

图2 Double Dueling DQN原理框图
2.2 NL-DQN分类预测模型的构建
在实际的分类预测问题中,往往存在大规模的状态空间与动作空间,内存往往是不能满足建立这样的Q表,因此传统的Q-Learning算法可能会引起维度灾难问题。利用深度神经网络对Q-Learning网络进行参数化逼近,也是深度强化学习模型的构建机理。
2.2.1双神经网络Double-DQN算法
由于深度Q网络在选择动作与动作评估时都选取了贪婪策略,且使用同一个神经网络参数,在学习过程中容易造成值函数过估计,即估计的值函数比实际值要大,因此会影响最终的最优策略。针对此问题,Hasselt等[13]提出Double Q-learning算法,对选择动作和动作评估进行解耦,以解决传统的Deep Q Network(DQN)过估计问题。本文以DQN为基础,融合了Double Q-Learning算法思想,构建了具有双神经网络的Double-DQN算法[12],2个神经网络中的一个用于选择动作,另一个用于对当前状态的价值进行评估。
Double-DQN算法首先在当前Qθ网络中找到最大Q值对应的动作,再由选择出来的动作a在目标网络Qφ中计算目标Q值,如式(10)所示:
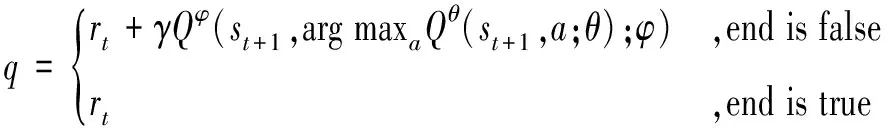
(10)
式中:q是目标Q值,Qθ是当前网络,Qφ是目标网络。
为保证模型Q值预测的准确性,采用ε贪婪策略[16]选择动作,即以概率1-ε按照Q值选择动作,以概率ε随机选择动作。利用式(10)目标函数和经验回放机制,最小化损失函数来训练Q网络。
2.2.2Dueling DQN 模型
传统的强化学习,考虑的是当前状态下的智能体采用哪个动作能获得最大的累计奖赏值,没有考虑到智能体在不同状态下采用不同的动作的方法。因此,本文采用了Dueling DQN[14]模型,该模型是采用2个相同的网络拟合不同的函数,一个是状态值函数V(s),另一个是智能体在当前状态下采取不同动作的优势函数A(s,a)[14],将得到的状态值函数V(s)及优势函数A(s,a)再进行线性组合,得到最终的输出Q值。如式(11)所示:
Q(s,a)=A(s,a)+V(s)
(11)
这与传统DQN仅利用卷积神经网络拟合Q-learning中的Q值函数是显著不同的。这种构造上的不同,有助于缩小Q值范围,提高模型的稳定性。
2.2.3损失函数的改进
损失函数是深度强化学习中一个重要组成部分,损失函数通过最小化模型的估计值与实际值的差值,从而提高神经网络的稳定性与加快收敛过程。传统的神经网络通常采用了均方误差损失函数(mean square error,MSE)拟合Q网络,但是该损失函数的缺点在于,当模型的时间差分误差较大时,输出的值过大,导致学习不稳定。平均绝对误差损失函数(mean absolute error,MAE)是线性的,在误差很小时,梯度也很大,对模型的收敛与学习有抑制作用,且在0处不可导。文献[20]中提出了Huber损失函数,该函数结合了MSE与MAE二者的优点,其定义如式(12)所示:
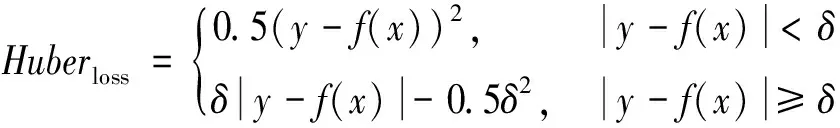
(12)
式中:δ是非负参数,划分二次函数与线性函数的范围。当误差大于δ时,采用MAE损失函数,当误差小于δ时,采用MSE损失函数。
由于Huber损失函数存在对离群点的惩罚程度过大的缺陷,为此,提出了一种新的分段损失函数nloss,用来提高模型的分类预测性能,其定义如式(13):
(13)
式中:n为非负变量,控制了损失函数的非凸程度。当n趋于无穷大时,该式等价于Huber损失函数。第一个式子保证了损失函数在中心点处可导;第二个式子具有非凸性,可降低对离群点的惩罚程度,且此损失函数处处可导。其中,f(x)是当前Q网络,q为目标值。下面给出对nloss损失函数的理论证明。
证明1:该损失函数处处可导且连续。
令q-f(x)=t,则
1) 在t=0处采用的均方误差损失函数,显然该式在0点可导。
2) 在t=1处
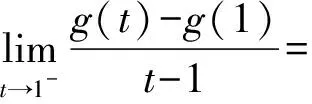
由于g′+(1)=g′-(1),因此该式在1点可导。
3) 在t=-1处

由于g′+(-1)=g′-(-1),因此该式在-1点可导。
综上,nloss损失函数处处连续且可导。
证明2:非凸鲁棒性。
当式(13)预测值与真实值误差小于1时,采用在零点可导的均方误差函数,当误差大于1时,采用更具鲁棒性的函数。在误差大于1时,采用的是非凸的函数,为了降低对离群点的惩罚程度,当前值与目标值突变时,该式可以起到在差值较大时对损失函数的弱化效果。如图3所示为n取0.5时的情况。

图3 n=0.5时nloss损失函数曲线
由图3可以看出,预测值与真实值误差大于1时,图像是非凸的,误差值越大,损失函数的斜率越小,可以对离群值起到弱化效果。
3 实验与结果
3.1 数据集
选用UCI数据集中4组数据集wine、glass、WDBC、ionosphere进行分类预测实验,以验证模型的性能。数据集的相关信息如表1所示。
本文采用的脑卒中发病风险预测数据集从国内某医院神经内科脑卒中筛查病例数据库获取,经过数据清洗等预处理后整理得到数据集stroke。该数据集包含41个属性,共1 538例样本。诊断类别包括脑梗死(1 064例)、脑出血(251例)、TIA(12例)、未破裂颅内动脉瘤(103例)、自发性蛛网膜下腔出血(76例)、动静脉畸形AVM(12例)、颈动脉狭窄或闭塞(33例)以及烟雾病(5例)8种。预处理后的部分脑卒中数据示例如表2所示。

表1 UCI数据集
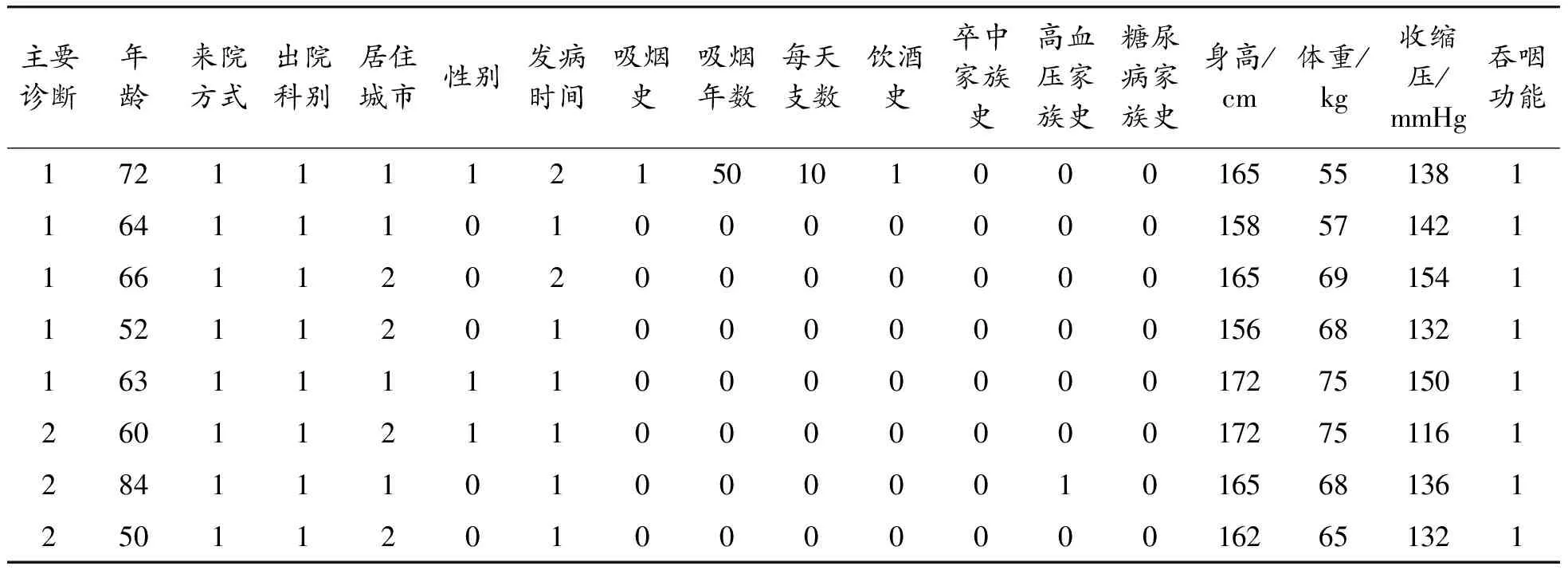
表2 预处理后的部分脑卒中筛查数据集示例
3.2 混合特征降维实验
3.2.1UCI数据集实验
实验选取的数据集是ionosphere数据集,该数据集有34种特征属性,2种类别。为了防止过拟合,本实验采用了十折交叉验证方法。分别使用CFS算法、信息增益算法(Information Gain,InforGain)算法、Relief算法以及FS-FE混合式特征降维方法获取最优特征子集,接着分别选用朴素贝叶斯算法(Naïve Bayes)、J48决策树算法、支持向量机算法(support vector machine,SVM)、最近邻算法(K-nearest neighbor,KNN)进行分类预测。准确率如图4所示。
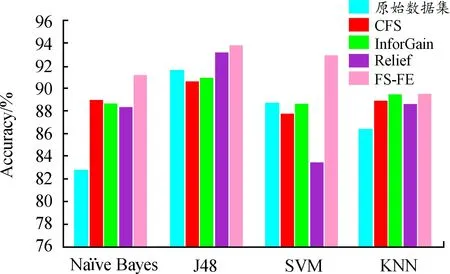
图4 FS-FE与其他特征降维算法的准确率
由图4可以看出,本文的FS-FE混合特征降维方法在所有的分类模型上均有良好表现,准确率都高于其他特征选择算法。其中,在SVM分类器模型下的准确率提升最为明显,对比原始数据集(下文均指代不使用特征降维算法)、CFS算法、InforGain算法、Relief算法,FS-FE方法的准确率分别提高了4.82%、5.84%、4.82%、11.26%。在Naïve Bayes、KNN分类器上,4种特征降维算法的性能均优于原始数据集,FS-FE方法准确率分别达到了91.17%与89.45%,取得了更优于其他特征选择算法的性能。此外,J48决策树分类模型的准确率在4种分类器中整体表现最好。
图5与图6分别显示了通过特征降维与分类模型后的精确率(precision)与召回率(recall)结果,可以看出,FS-FE方法比其他特征选择方法的精确率与召回率性能更好。
根据图5可以看出,FS-FE方法的精确率明显高于其他特征选择方法。在Naïve Bayes、J48、SVM和KNN 4种分类模型上的精确率分别是91.20%、93.90%、92.90%和90.80%,都在90%以上,体现了FS-FE特征降维方法与不同分类器的适配性,在泛化能力方面也有良好表现。在上述4种分类器上,FS-FE方法对比CFS算法精确率分别提高了0.66%、3.64%、4.97%、1.23%,说明了FS-FE特征降维方法的优越性。
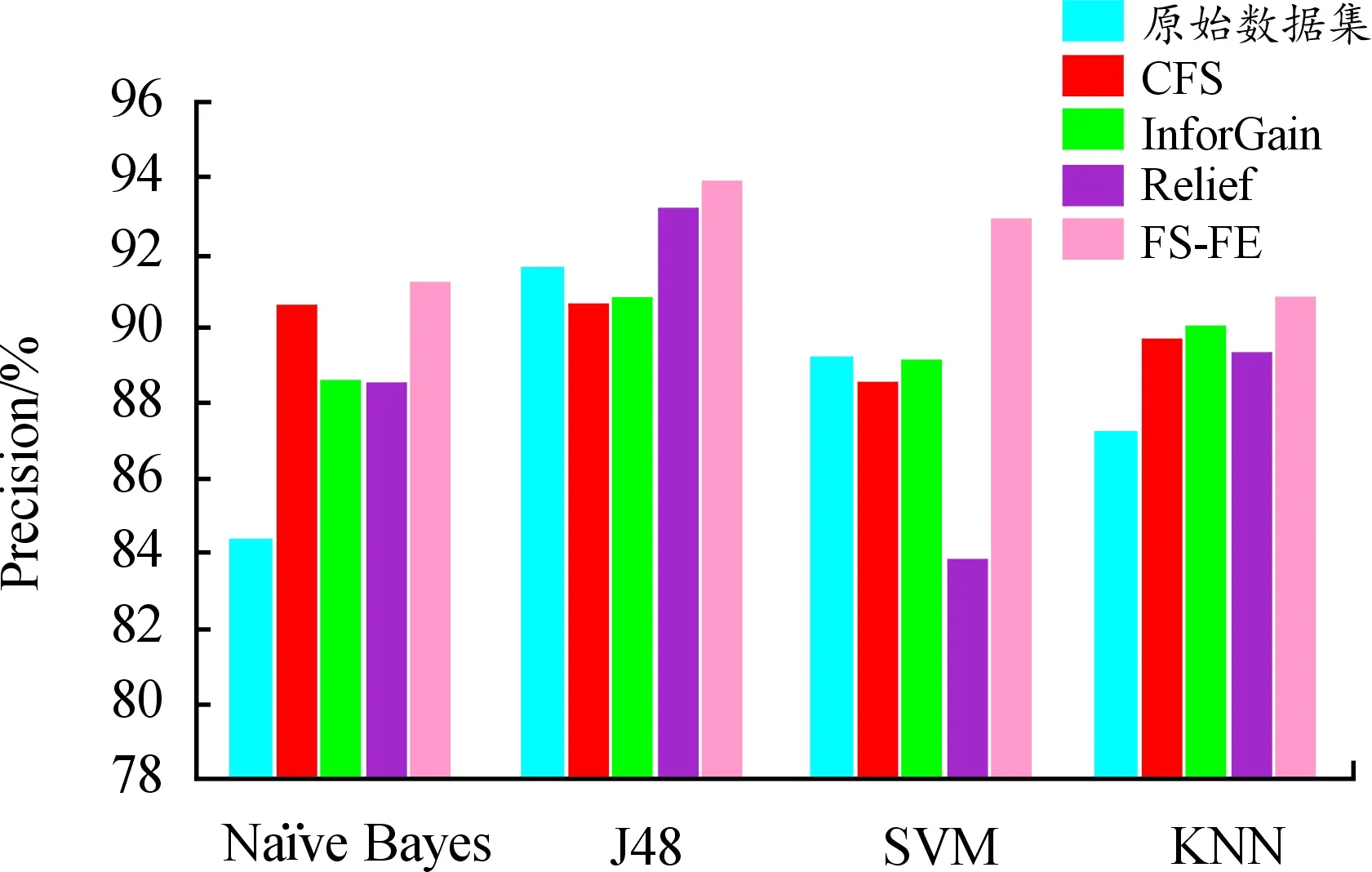
图5 FS-FE与其他特征降维算法的精确率

图6 FS-FE与其他特征降维算法的召回率
观察图6召回率性能实验结果,FS-FE特征降维方法在所有的分类模型上都取得了最好的效果。以Naïve Bayes与J48分类器举例说明,在Naïve Bayes分类器上,FS-FE算法的召回率为91.20%,与原始数据集、CFS算法、InforGain算法和Relief算法对比,召回率分别提高了10.41%、0.66%、2.93%、3.28%;在J48分类器上,FS-FE与原始数据集、CFS算法、InforGain算法和Relief算法对比,召回率分别提高了2.40%、3.42%、3.08%和0.54%。
综上所述,混合式特征降维方法FS-FE可以有效提升分类效果,在各个评价指标上都有良好的性能表现。
3.2.2脑卒中筛查数据集实验
为了对比本文中提出的MCFS算法进行特征选择的优势,将其用于脑卒中筛查数据,分别与CFS算法、信息增益算法、Relief算法对比,结果如表3所示。
MCFS算法选出的对脑卒中的诊断类别的重要影响因素有7个:是否抗血(33)、出院科别(3)、是否调脂(36)、同型半胱氨酸(31)、评分数(40)、是否降压(40)、发病48 h内是否给药(34)。与CFS区别仅在于发病时间距住院时间是否小于14 d(6)以及同型半胱氨酸(31)。其他2种方法得到的影响因素也包括33、36、40、35、34五个特征,这与临床重要影响因素结论一致,但本文特征选择算法MCFS得到的同型半胱氨酸(31)因素与已有CFS和Relief算法得到的因素发病时间距住院时间是否小于14 d(6),以及InforGain算法得到的来院方式(2)、高密度脂蛋白胆固醇(30)等其他因素相比,对脑卒中诊断更重要,说明本文方法的有效性。

表3 4种特征选择算法选择的特征子集
接着分别选用Naïve Bayes、J48、SVM、KNN算法对特征选择前后的数据集进行分类预测,为了防止过拟合,采用十折交叉验证方法。
表4为FS-FE方法与其他方法在脑卒中筛查数据的准确率,可以看出FS-FE方法在不同的分类模型上都取得了最好的结果。在Naïve Bayes分类模型上,FS-FE方法对比原始数据集、CFS算法、InforGain算法和Relief算法,准确率分别提高了7.18%、3.72%、9.62%和2.79%。在所有分类器上,采用FS-FE算法时,脑卒中筛查数据集的分类准确率均在80%以上,验证了改进的算法具有良好的预测性能。
由上述实验结果与分析可知,混合式特征降维方法FS-FE可以在不同的分类模型上获得更好的准确率、精确率与召回率,其分类预测性能优于其他特征选择算法,可以为脑卒中疾病辅助诊断提供建议。

表4 FS-FE方法与其他方法在脑卒中筛查数据的准确率 %
3.3 NL-DQN分类预测模型
本文使用Pytorch 0.4 搭载预测模型,本文的神经网络包括输入层、隐含层以及输出层。各层的神经元设为128,输出层加上softmax用于进行分类预测。神经网络的初始学习率设置为0.000 5,并随着训练次数退火直至0.000 000 1,折扣因子设为0.95,线性衰减的ε值设为1,每10步衰减直至0.1。本文实验采用交叉验证方法,并划分数据集为训练集60%,验证集20%,测试集20%。其中,训练集用来训练分类预测模型,验证集用来优化模型,测试集用来检验模型性能。
为证明本文所提模型的有效性,采用Naïve Bayes、SVM、KNN以及使用MSE的DQN算法[12]、使用MAE的DQN算法的分类预测模型作为对比实验,进行模型的性能测试。本节选用准确率对预测模型的性能进行评估。
将所选数据集采用特征降维方法FS-FE去除冗余特征,接着将最优特征组合使用NL-DQN模型进行脑卒中风险预测。
3.3.1UCI数据集实验
为验证所提模型的有效性,采用前述4组UCI数据集wine、glass、WDBC、ionosphere进行分类预测实验,验证模型的性能。表5为本文方法与已有模型准确率。
由表5可知,除了WDBC数据集外,NL-DQN模型在3个数据集上与其他模型相比,都可以取得最好的分类性能。其中在wine数据集上,NL-DQN模型相比较Naïve Bayes、J48、SVM、KNN、DQN(MSE)以及DQN(MAE)分类模型,准确率分别提高了4.49%、5.22%、5.28%、6.20%、1.31%、2.67%。在WDBC数据集上,NL-DQN模型准确率比DQN(MSE)及DQN(MAE)稍有降低,不过降低幅度较弱。此外,NL-DQN模型的分类效果较之其他经典分类算法性能都更好。说明NL-DQN分类预测模型总体而言具有较优的分类预测效果。

表5 NL-DQN模型与已有模型在UCI数据集的分类准确率 %
3.3.2脑卒中筛查数据集实验
将所提模型用于脑卒中筛查数据集。NL-DQN模型与已有模型在脑卒中筛查数据集的分类准确率如图7所示。

图7 NL-DQN模型与已有模型在脑卒中筛查数据的分类准确率
由图7可知,与Naïve Bayes、J48、SVM、KNN以及损失函数为MSE、MAE的DQN模型相比,NL-DQN模型在脑卒中数据集的准确率分别提高了12.65%、3.20%、4.77%、8.17%、3.96%和2.21%,验证了本模型用于脑卒中筛查数据集性能的优越性。
以上实验可以说明,NL-DQN模型的分类预测性能在不同数据集上,总体优于Naïve Bayes、J48、SVM、KNN、DQN(MSE)以及DQN(MAE)分类模型,充分验证了NL-DQN模型的有效性。
4 结论
提出了一种FS-FE混合式特征降维方法,为使特征选择不受属性取值个数的影响,该方法采用MIC对CFS算法进行改进,结合改进的特征选择算法与特征提取算法对特征进行混合降维,对分类性能有良好的作用。设计了基于Double DQN和Dueling DQN算法的脑卒中发病风险分类预测模型NL-DQN,提出了一种更具鲁棒性的损失函数。结果表明,NL-DQN模型与已有算法相比,在UCI数据集、脑卒中筛查数据集中的准确率均有提高。但本文模型未考虑脑卒中筛查数据呈现的数据不平衡现象,下一步研究将针对数据集不平衡特点对模型进一步优化。
