基于“计算简便”的心理因素对“物质的量”的教学思考

任圣颖

摘要： “计算简便”是科学家引入物质的量的心理因素，为了降低该知识点的抽象性，基于“计算简便”思想，利用函数作为工具，依次引出阿伏伽德罗常数、摩尔、物质的量，使这些知识点“去抽象化”。

关键词： 计算简便； 物质的量； 摩尔； 阿伏伽德罗常数； 化学教学

文章编号： 1005-6629（2023）02-0095-03

中图分类号： G633.8

文献标识码： B

“物质的量”是高中化学最基础的概念，贯穿于整个高中化学学习中。人教版、鲁科版和苏教版教材均将“物质的量”内容放在高一上学期学习，但由于“物质的量”内容抽象，给学生的学习和教师的教学带来了巨大的挑战，该知识点是公认的教学重难点。

人教版化学必修第一册教材在物质的量知识点引入时有如下叙述：“那么，对化学反应进行定量研究时，能否将可称量的物质与难以称量的微观粒子之间联系起来呢？为此，国际上采用了一个新的物理量——物质的量”［1］。许多教师依此设计教学方案，将物质的量联系宏观和微观的“桥梁作用”放在教学的核心位置。这种教学方案的优点毋庸置疑，但学生在初学物质的量时，面对这种具有抽象性的知识点时，常常充满疑惑：如果没有这个“桥梁”，不是更加直观吗？为什么要引入这样一个“桥梁”呢？本文认为，面对学生这样的疑惑，最需要的是给出“追本溯源”式的解释。也就是从化学史的角度，找出科学家“为什么引入物质的量”的心理因素。在教学设计上，如果能将这种心理因素考虑进教学方案里，则可能会有效破解物质的量教学难点，达到“势如破竹”的效果。

1  为什么要引入阿伏伽德罗常数及物质的量

阿伏伽德罗基于原子论提出了一个假设（即阿伏伽德罗定律）：在同温同压下，相同体积的任何气体都含有相同数目的分子。其数学表达式为V=C（T， P）N，其中V为气体的体积，N为气体分子数，Ｃ为比例系数。在随后对此假说进行研究时，由于气体分子数量庞大，为了方便计算［2］，科学家引入常数对其进行简化：

N→N常数

上式中的“常数”可以是任意一个合适的、比较庞大的数值，但考虑到相对原子、相对分子的数值，为了计算方便，科学家规定此“常数”乘以每个分子的质量得到的数值应该与其相对分子质量相等。因此，“质量的数值与相对分子质量相等”的某物质包含的分子数就是这一常数的值，由于目前我们不能十分精确测量每一个分子（原子）的质量，因此科学家们只能知道这一常数约为6.02×1023。需要说明的是，这一“约”，并不是对这一个已知的数字的“约”，而是一个对未知数字的“约”。

为了表达的合理性，科学家引入物质的量n，单位为mol，以维持简化后分子数的完全等效性：

n=N6.02×1023mol

否则数字简化后则会引起错误、混淆，比如：

N=6.02×1023，对其进行简化，N常数=N6.02×1023=1，简化后失去了真实的分子数。将n=N6.02×1023mol变形可得：n=N6.02×1023mol-1，而6.02×1023mol-1被科学家推荐命名为阿伏伽德罗常数，以纪念科学家阿伏伽德罗。

在科学发展史上，人们用π符号表示圆周率、利用科学计数法和对数法等对数字进行处理，都是为了简化数字，以达到“计算简便”的目的。由以上论述我们发现，阿伏伽德罗常数、物质的量的引入，类似于科学计数法、对数法的发明，直接原因都与“计算简便”有关。物质的量具有连结宏观和微观“桥梁的作用”，但这种“桥梁的作用”并不是引入物质的量的直接目的。因此，如果依照化学史的角度来看待物质的量引入问题并以此为基础设计教学方案，我们必须要考虑“计算简便”这一心理因素。2018年，国际计量大会将摩尔定义为：1摩尔精确包含6.022214076×1023个基本粒子。上述所述未知数字的常数变成了一个确切的、已知的数字。这一重新定义，是基于计量的准确性和等效性来考量的，但究其心理因素，也是为了达到“计算简便”，因为一个“不确定的常数”必然带来计算的复杂性、不确切性和不等效性。

2  简要教学设计思路

从阿伏伽德罗常数的引入到摩尔的重新定义，贯穿其中的心理因素是“计算简便”。因此，如果能以“计算简便”的心理因素贯穿物质的量的教学，还原科学家引入物质的量的过程，必然能有效降低知识点的抽象性，更容易实现“宏观辨识与微观探析”的核心素养目标。

2.1  计算简便的需要：引入常数

［教师］在化学中，多数情况下，粒子数量都比较庞大，比如，18g水含分子数约为6.022214076×1023。“6.022214076×1023”在化学计算、记录中比较麻烦，我們能否设计一个函数使庞大的数字简化？科学家首先想到的是除以一个常数，即设计函数f（N）=NC，将数字N除以一个常数C。由于在化学计量中，N值一般很大，常数C选多大为好呢？

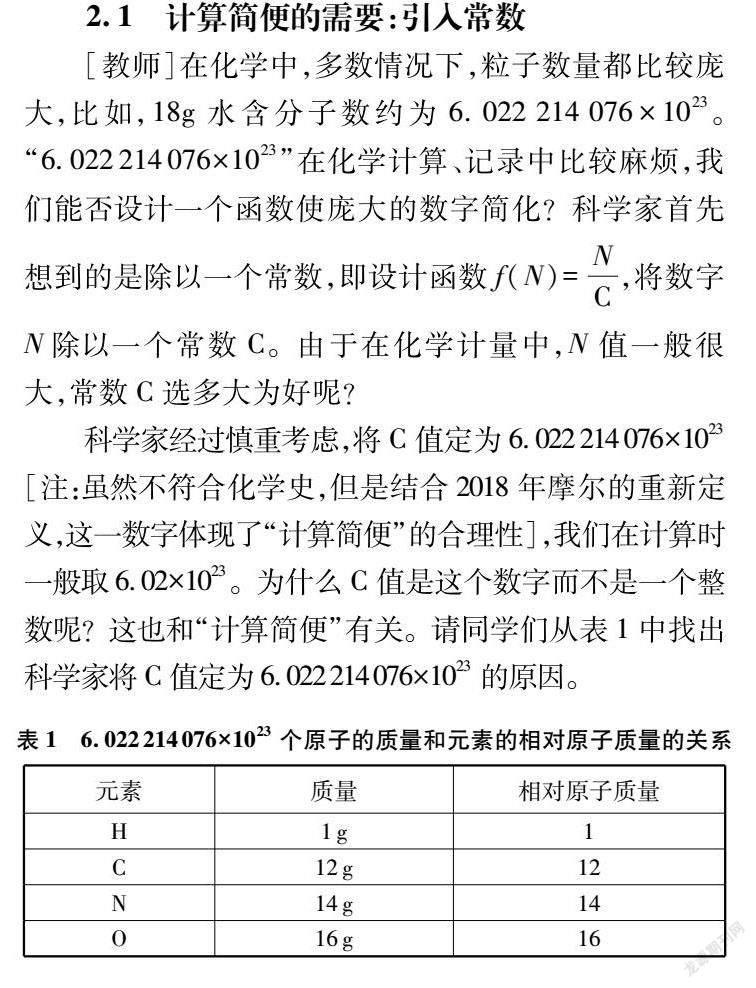
科学家经过慎重考虑，将C值定为6.022214076×1023［注：虽然不符合化学史，但是结合2018年摩尔的重新定义，这一数字体现了“计算简便”的合理性］，我们在计算时一般取6.02×1023。为什么C值是这个数字而不是一个整数呢？这也和“计算简便”有关。请同学们从表1中找出科学家将C值定为6.022214076×1023的原因。

2.2  等效性的需要：引出阿伏伽德罗常数、摩尔、物质的量

［学生任务］利用f（N）=N6.02×1023对数字简化。18g水含水分子数约为6.02×1023。

简化前：分子数=6.02×1023  简化后：f（6.02×1023）=6.02×10236.02×1023=1。

［教师］很显然，通过上述方法，6.02×1023数字得到了极大的简化。但问题是，简化后的“1”能够代表分子数“6.02×1023”的含义吗？简化后是否具有等效性？

［学生讨论，教师总结］我们叙述18g水含有的水分子数为6.02×1023没有问题，但如果叙述18g水含有的水分子数为“1”，很显然存在问题，6.02×1023≠1。

那么该如何解决这一矛盾呢？为了使简化前后数值具有完全等效性，科学家将简化后数字“1”加上一个单位——摩尔（符号为mol），以区别普通数字1。

即简化后：f（6.02×1023）=6.02×10236.02×1023=1→1mol

f（2×6.02×1023）=2×6.02×10236.02×1023=2→2mol

如果使函数f（N）带上单位mol，我们需要将函数f（N）修改为f（N）=N6.02×1023mol-1，而6.02×1023mol-1，科学家将这个带有单位的常数叫做阿伏伽德罗常数，符号为NA=6.02×1023mol-1。

［教师］结合教材，解释阿伏伽德罗常数单位的含义：每摩尔，即1mol粒子集合体所含的粒子数为6.022214076×1023，约为6.02×1023。

2.3  概念逻辑的需要：引出物质的量

［教师］结合图1说明：通过以上过程，我们发现，函数f（N）的作用是将粒子数N通过阿伏伽德罗常数压缩成集合体。

f（N）=N6.02×1023mol-1，科学家将f（N），这一表示粒子集合体的函数，称为“物质的量”。

例如：我们说18g水含有的水分子的个数=6.02×1023，但我们怎么叙述：经过函数f（N）压缩，18g水含有的水分子的________=1mol？36g水含有的水分子的________=2mol？……？  答案是“物質的量”，也就是上述函数f（N）。从逻辑学的角度而言，这里需要填写一个能体现水分子数集合体的概念，所以不能再使用“个数”。

3  结语

与大多数教学设计思想不同的是，本文基于“计算简便”心理因素，利用函数说明引入“阿伏伽德罗常数”的作用，这要比基于“桥梁”思想设计教学方案更容易去抽象化，也更符合科学家引入物质的量这一基本物理量的实际过程。基于此思想的教学设计，层层递进，能够让学生清楚地了解，为什么我们需要先搭建物质的量这座“桥梁”，而不是直接体现桥梁的意义。

参考文献：

［1］王晶， 郑长龙主编. 普通高中教科书·化学必修第一册［M］. 北京： 人民教育出版社， 2019： 49.

［2］林则东. 论阿伏伽德罗常量［J］. 物理通报，2017， （8）： 128～129.