低年级数学单元结构化设计的研究

福建厦门英才学校（361022） 叶妙妙

美国心理学家和教育学家布鲁纳认为，掌握一件事物的结构，就是理解它与其他事物之间的意义的联系。简单地说，学习结构就是学习事物是怎么相互关联的。

课堂框架不应是线性的，而应该要系统地设计，通过对教材的解读、重整进行结构设计，做到教结构、用结构，实现“整体—部分—整体”的目标。教师要从低年级开始有意识地进行结构化设计，坚持每一节课都有高标准的引领和融合渗透，努力让学生建构知识体系，从而培养学生主动迁移的意识，为学生今后进行知识关联、思维活动奠定基础，促进学生深度思考。图1 是笔者探索出来的关于单元教学结构化设计的总思路。

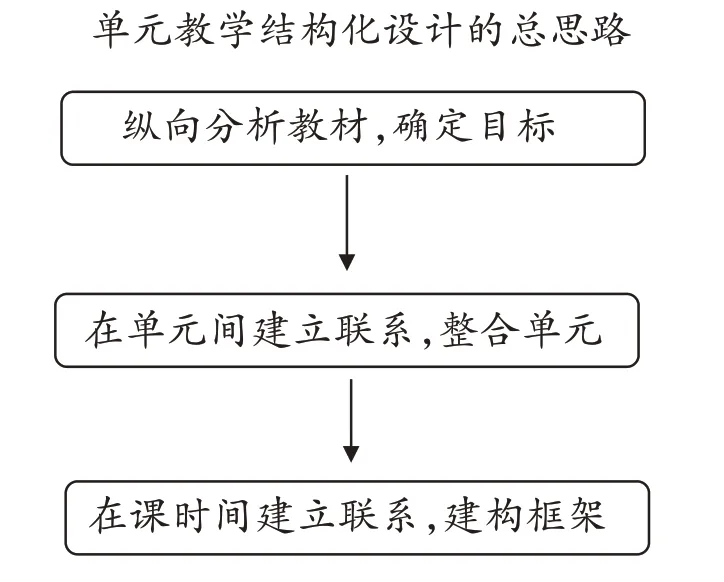
图1

一、整体入手，分析教材

教师在对教材内容进行结构化设计时，要从整体知识纵向分析教材，既要理解整体知识的总目标及分学段、分单元、单课时的具体目标，又要处理好知识的整体与局部的关系，了解知识背后蕴含的学科育人价值。教师要站在更高的角度，打破年级界限，从知识的整体高位进行分析，才能更好地把握学段、单元、单课时的育人目标，做到心中有底、长远规划。例如，笔者分析第一学段“数的认识”编排时，发现教材将“数的知识”分散安排在不同的年级（见表1）。

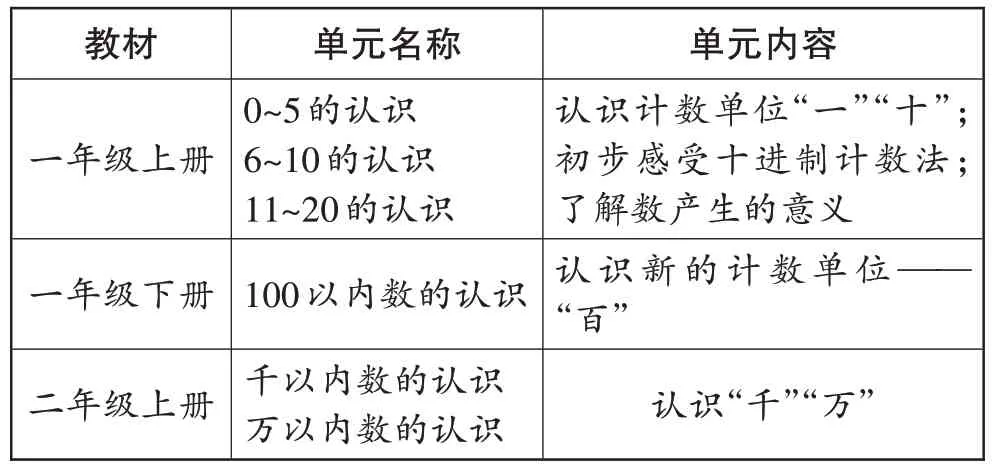
表1 “数的认识”在一、二年级的编排情况

从表1 可以看出，“数的认识”让学生经历数的形成和拓展的过程，感悟数的结构。每个年级关于“数的认识”的安排都不可忽视，“20 以内数的认识”是学生认识数的起点；“100 以内数的认识”是学生建立位值制的关键；“千以内数的认识”让学生加深理解十进制位值制，深刻理解数的本质，为学习更大的数奠定基础。教师要引导学生在把握数的构造的基础上不断认识新的数，让学生从本质上建立起数与数之间的联系，了解、感受前人创造数的智慧。从长远发展来考虑，学生在一年级时掌握的数的结构，对其进一步认识其他数有重要作用。因此，从整体知识纵向分析教材是进行结构化设计的前提。

二、单元整合，结构设计

结构化教学，需要教师用结构化思想，从教材内容出发，对教材进行整体规划，打破单元界限，将不同的单元进行整合，使知识系统化。

一年级上册关于“20 以内数的认识”的内容，教材分了三个单元（1~5 的认识、6~10 的认识、11~20 的认识）。笔者尝试整合这三个单元，从单元知识间的逻辑关系进行整体思考，使知识间的联系更为紧密，突出知识间的本质关系，利于学生主动构建知识体系。

1.积累经验

数都是数出来的，但要怎么数才能为后续学习奠定基础？笔者在“1~5 的认识”单元，就引导学生用计数单位“一”数数（1个一、2个一、3个一……）。学生在数的过程中，逐渐地有了以“一”为单位的数数经验，理解“几个一就是几”，为认识新的计数单位“十”奠定基础。

2.概念前置

“6~10 的认识”单元，“10 的认识”作为一个独立的课时，目的就是让学生深刻地理解“十”的概念，但教材却在“11~20 的认识”单元的第一课时才揭示新的计数单位“十”。基于对学生学情的分析，笔者尝试将“1 个十”的概念前置到“10 的认识”一课进行教学，将“10 个一”与“1 个十”通过摆小棒联系起来。

3.迁移类推

在学习“11~20 的认识”时，学生不仅通过摆小棒直观理解数的概念，还通过计数器初步感受位值。在“实物操作+半直观模型+建立表象”的基础上，笔者通过课件整体呈现小棒图及对应的数字符号（如图2）引导学生观察发现：十加几就是十几。

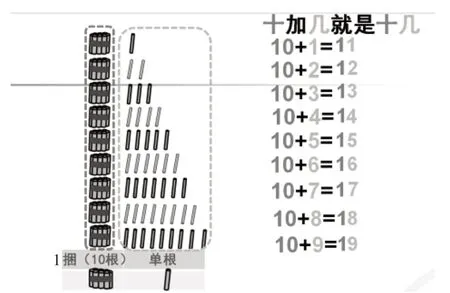
图2

这有利于让学生直观感受数与数的运算的联系。同时，学生在进一步探究“10 加一位数及相应的减法”时，也能自主迁移，即利用脑海里数的组成的表象进行探究，将学习经验迁移到学习新知识的过程中。教师在课堂上大胆地放手，让学生充分地交流、表达自己的想法，能促进学生进行深度思考，同时获得良好的学习体验，这正是因为教师打破单元界限，有机地融合并进行结构化教学才出现的良好局面。

三、知识关联，构建体系

数学教学的重要价值是培养学生的思维品质、数学素养，培养学生主动学习的习惯。教材将数的运算安排在不同学段的不同单元里，每个单元都是一个相对独立的知识块。这样的编排让学生学到的知识碎片化，没有形成系统的知识链。没有联系的知识学起来比较吃力。因此，教师有必要对单元知识进行结构化设计，联系前后知识，尤其是在起始课上渗透算理，并将算理迁移到后续内容中。由点及面进行结构化设计，更利于学生在学习过程中思考。

1.分析教材

以“20 以内进位加法”单元为例，本单元的起始课是“9 加几”。教材分三个阶段由具象到抽象地呈现本单元内容：第一阶段是“9 加几”，主要通过具体的操作、直观的表象建立“凑十”的模型，让学生在理解算理的基础上掌握算法；第二阶段是“8、7、6 加几”，进一步巩固“凑十”法，需要学生逐步抽象，借助表象进行口算；第三阶段是“5、4、3、2加几”，则更为抽象，鼓励学生利用“和不变的规律”进行推算。从单元的整体进行分析，教师可以用“教结构，用结构”的结构化设计，沟通单元知识间的联系，提升学生的结构化思维。

2.结构化设计思路——教结构，用结构

基于教材分析，“20 以内进位加法”单元的主要编排思路是把重点放在“9 加几”这节课上，形成口算“9 加几”的思路，让学生感受其中的数学思想方法，再将数学思想方法迁移到“几加几”的学习上。笔者对“9加几”进行如下结构化设计。

（1）动手操作，建立表象。着重让学生在经历“凑十”的具体操作后将数与形结合，引导学生在脑海里想象“凑十”的过程。

（2）观察比较，理解算理。通过多媒体课件呈现“9+2，9+3，9+4，…，9+9”8 道算式和对应的小棒直观图，让学生通过观察发现“和的个位上的数比另一个加数少1”的规律，同时引发学生的疑问：少的“1”去哪了？笔者启发学生通过直观图（如图3）发现：少的“1”其实与9 凑成了十。这一过程其实是引导学生进行深度思考，理解算理，从而实现“具体操作—形成表象—回到具体”的目标，为进一步抽象做准备。

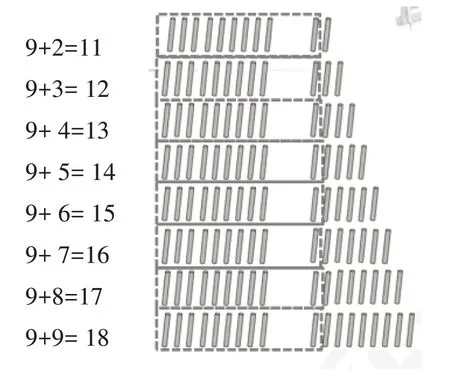
图3

（3）想象操作，建立模型。在第（2）环节的基础上，进一步引导、鼓励学生在脑海里想象小棒“凑十”的过程，在想象中加深理解并建立“凑十”的模型，进而掌握算法。当然，除了“凑十”法，我们也鼓励学生有不同的方法。

学生有了认知经验和方法基础，学习“8、7、6加几”时自然要联系学过的知识，唤醒原有的认知经验。教师大胆放手，引导学生进行方法的迁移后，提出有针对性的问题：“‘8、7、6加几’与‘9加几’的口算思路有什么相同点与不同点？”让学生去观察、讨论、交流，目的是把问题引向深处，让学生发现数的本质，并感受知识间的紧密联系，体验学习数学知识与方法是从特殊到一般的过程，初步感受建模思想，提高学生的数学运算能力、推理能力。有了学习基础，学生学习“5、4、3、2 加几”就更是得心应手。在这一过程中，学生加深了对数学方法的理解，提高了数学思维能力和数感。

经过结构化设计的课堂让笔者倍感欣喜，即使是低年级的学生，他们的思维也不再停留在表面，而是透过现象看见数学的本质，并能深入思考数学知识。同时，学生获得了良好的学习体验，增强了学习信心，提高了数学能力。结构化课堂是灵动的、充满活力的，学生真正置身于课堂，学到了真正有用的数学知识和能力，在学生成长的同时，教师也获得了成长。引用李政涛教授的一段话：“不生长的课堂是无效的课堂，被生长的课堂是僵化的课堂，自生长的课堂是绿色的课堂，当然，共生长的课堂是理想的课堂。”理想的课堂是师生能共同成长的课堂，教师应努力设计结构化课堂，尽力实现师生共同成长。