对一道相互独立事件问题的解法的探究

金红立

相互独立事件是概率板块中的重要内容.若事件 A（或B）是否发生对事件B（A）发生的概率没有影响， 则这样的两个事件叫做相互独立事件.设A、B是两个 事件，如果满足等式 P（A ∩ B）= P（AB）= P（A）P（B） ，则称 事件A、B相互独立.相互独立事件问题的常见命题形 式有：（1）判断两个事件是否相互独立；（2）求相互独 立事件的概率.下面通过剖析一道例题，探讨一下判断 两个事件是否相互独立的方法.

例题：已知袋中有除颜色外都相同的 3 个白球和 2 个黑球，依次不放回地摸出2个球，设事件A为“第1 次摸到白球”，事件B为“第 2 次摸到白球”.试判断事 件A、B是否为相互独立事件．

仔细分析题意可知，取出一个白球或一个黑球， 相互不影响，所以事件 A 是否发生对事件 B 的发生没 有影响.由相互独立事件的定义可知，需先求得事件 A 、B 的概率，然后判断P（AB）与P（A）P（B）的关系，才能 判断出事件 A、B 是否相互独立.解答本题主要有以下 几种方法.

一、枚举法

枚举法是将所有的情况一一列举出来的方法.采 取枚举法，可以快速明确事件发生与否的所有情况， 从而快速确定样本空间中的每个样本点和问题中所 求事件的样本点，再根据概率公式即可求得事件的概 率.

解：

在采用枚举法解题时，不能重复、不能遗漏任何 情况，以确保答案的正确性.

二、列表法

该方法较为简单.运用列表法判断两个事件是否 相互独立，需通过列表，找出样本空间中的每个样本 点和问题中所求事件的樣本点，统计出相应的数据， 即可求得事件的概率.

解：

对于数据不多，或可能出现的情况较少的问题， 都可以采用列表法求解.但需注意合理设计表格，并做 好数据统计.

三、坐标法

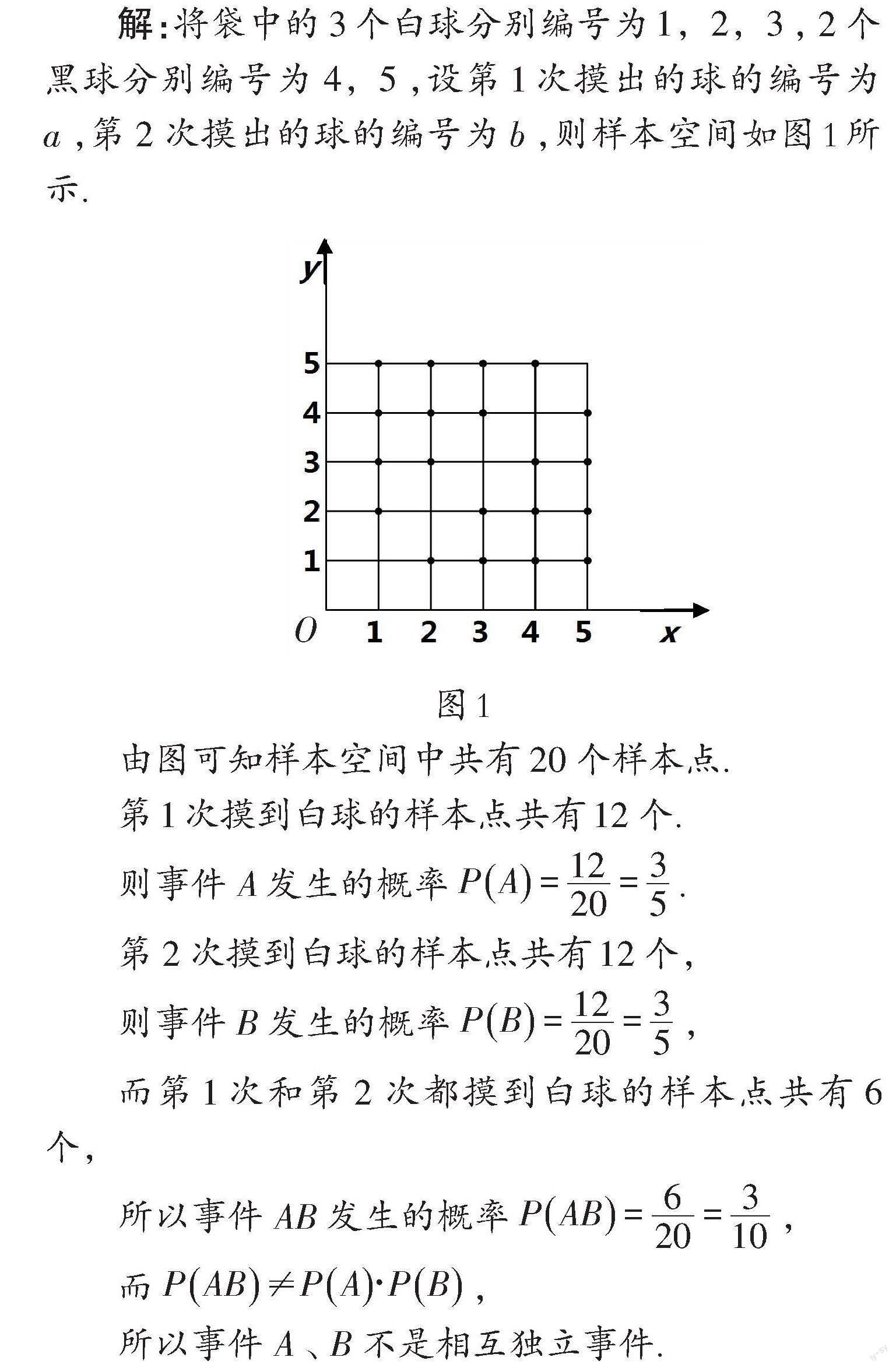
对于含有双变量的概率问题，通常可采用坐标法 求解.该方法与列表法较为相似，不同的是，需将变量 的取值作为坐标轴上的点.先画出坐标系，确定坐标系 上所有可能取的点，然后进行统计，即可根据概率公 式求出概率.

解：

由于事先无法确定两次摸到的球的编号，因此把 它看作两个变量，并且所有的变量都为正整数.然后画 出坐标系，在坐标系中统计出两次摸到编号为1、2、3 的球的次数，即可求出取得白球的概率.

四、画树状图

运用树状图法解题，需用树状图列出样本空间中 的每个样本点和问题中所求事件的样本点.在画树状 图时，要按照一定的顺序罗列出各种情形，确保不重 复、不遗漏任何情形，再求出事件的概率，进而利用相 互独立事件的定义判断事件的独立性.

解：将袋中的 3 个白球分别编号为 1，2，3 ，2 个黑 球分别编号为 4，5 .

通过画树状图来求事件A、B、AB的概率，比较便 捷，且不容易出错.

五、利用计数原理

在求事件的概率时，通常要用到两个计数原理： 加法计数原理和乘法计数原理.在解题时，要先考虑清 楚完成一件事件是否要分步、分类，若要分步进行，则 需采用乘法计数原理求解；若需要分类进行，则需采 用加法计数原理求解.

解：

在解题时，要先明确事件发生的各个环节中是否 有顺序、类别要求；再选用与之相应的计数原理解题.

总之，判断两个事件是否相互独立，关键在于判断 两个事件是否相互影响，根据概率公式，明确 P（AB） 与 P（A）?P（B） 之间的关系.同学们在求两个事件的概率时 可以根据解题需求，选取合适的方法进行求解.

（作者单位：江苏省徐州市铜山区夹河中学）