多层孔隙材料在建筑施工中的隔热机理及其优化设计

2023-04-03张伟超张磊王磊董自运古松

中国建筑金属结构 2023年2期

张伟超，张磊，王磊，董自运，古松

（1.中铁建工集团有限公司，北京 100160 ；2.中铁建工集团北方工程有限公司，天津 300450；3.西南科技大学土木工程与建筑学院，四川绵阳6 210000）

0 引言

多孔柔性材料因其独特的形状、尺寸以及结构拓扑特性，确定了其在重强比与热传导方面的显著优势，已广泛应用于工程项目的结构填充、隔热保温以及噪音处理等领域[1-3]。如低密度泡沫材料在结构填充中的应用，低导热率多孔材料在隔热保温中的应用。近年来，随着我国工程基建的迅猛发展，涌现了众多结构体量庞大的基础设施，这些工程项目由于内部空间大，跨越范围广，其功能需求也越来越复杂，对于大型复杂结构体，其于服役环境的热交换效果，直接决定其建筑能耗水平[4]。

文献[5]调研了湖南地区农村用房隔热保温层的选用设计状况，给出了华南华中地区民用建筑隔热保温层的应用状况。文献[6]介绍了发泡技术在建筑隔热保温层施工中的应用，验证了孔隙介入在建筑隔热保温层领域的适用性。文献[7]分析层数效应对建筑围护结构的热桥效应，研究了围护结构层数对建筑结构隔热保温效率的影响，给出了围护结构隔热效果随其防护层层数增加的结论。虽然目前隔热保温材料及其构造在热工效率与围护效果方面取得了长足发展，但多涉及平原内陆地区，对于高原强辐射环境尚未过多考虑。另外，当前隔热保温材料多考虑层数调控获得的热工效果优化，而未将其结构自身的孔隙特点综合考虑。

对于高原强辐射环境，外界辐照或温度水平与隔热保温层热工效果密切相关。一般而言，在大型复杂结构与周围环境热交换总量中，屋面体系的能量传导最大，约占耗散/传递总能的60%以上；其次为门窗洞口和围护墙体，但后两者的能量耗散/传导能量不到总能的40%。因此，针对大型复杂结构体，屋面工程的隔热保温效果对控制建筑总能耗起着关键作用。通常，大型建筑屋面体系多采用具有良好塑性和安装优势的薄壁冷轧轻钢结构，且钢结构中腔采用一定厚度的多孔材料填充，如软瓷保温材料、硅酸铝保温材料、酚醛泡沫材料、玻璃棉以及岩棉材料等[1-5]。在隔热保温体系设计上，均按照工作环境参数，基于热传导基本理论，进行隔层材料厚度设计。然而传热传质学早已明确指出，材料传热效率不仅由材料本身导热能力决定，还与材料组合形式有关，例如同种材料按照不同厚度的独立单层进行拼合，其隔热效果的量化水平是等厚度整体材料的指数倍。

基于此，本研究在建筑工程传统隔热保温设计方法上，将多孔隔热保温层沿厚度方向进行不同尺寸水平的拆分，形成多层组合形式，基于热传导学基本理论，研究单层多孔材料厚度对其热传导效果的影响，分析相同保温层厚度在不同独立单层组合方式下的热交换效果的变化与差异，确定出不同辐射条件下的最优隔热层组合方式，以期为建筑工程隔热保温体系设计优化提供理论依据。

1 多孔材料热工交换系数

众所周知，同种材料实体结构热工能力显著低于含孔隙结构，且孔隙形式对热工交换能力具有显著作用。一般而言，孔隙体积、形状样式以及排列方式均可对结构热工效率造成影响。因此，隔热保温材料内部均需构造出大量孔隙结构以保障其有效的隔热保温能力。

为进一步建立孔隙与材料热工效果之间的关系，人们提出了多种方法对多孔材料的孔隙特征指标进行量化，如反映孔隙尺寸及其分布的孔隙体积（率）、孔隙最大/小尺寸、孔隙密度以及孔隙尺寸统计参数，和反映孔隙形状的形状参数。但对于尺寸不一、形状各异的大量离散分布的内孔隙，单一采用尺寸参数或形状参数均无法很好表征其微孔集合与效果，故部分学者采用了综合表征法对多孔材料的微孔性质进行描述。

大量独立孔隙分散于热工材料内部，在突出结构特性的条件下确保了良好的热桥效应，孔隙尺寸、分布状态以及形态特征不同，材料热工交换系数不同，其热工效能也不同。由于引起孔隙材料热工导热的构造因素较多，因此在隔热保温构造措施热工理论分析时，多采用简化方法，即将材料孔隙构造采用单一指标进行评价。多孔热工材料的交换系数可表示为：

由公式（1）可知，多孔材料热工系数主要受其孔隙特征（尺寸、形状以及分布）与边界条件影响，而实际工程中隔热保温层边界多采用其他异类实体结构封堵，从而发生边界变异，但其自身内部孔隙特征受外界影响不大。基于此，通过调控材料内部孔隙特征参数可实现其热工特征的有效改变。

基于此，本文通过改变δ、ε 值可得到一系列单层多孔材料的热工系数变化曲线，如图1 所示。

由公式（1）可见，当独立孔隙不断缩小且不断加密，即δ →0，ε →0，热工系数T 必然存在最大值，即无论如何优化孔隙特征，其热工系数总会出现最优值，即最优热工系数。

由图1 可见，随着孔隙相邻平均间距δ 逐渐减小，隔热保温材料热工系数T 减小，且减小幅度逐渐加快。而不同ε 条件下，T～δ 变化关系差异较大，当ε 较大时，T 随δ 的变化幅度十分显著，而当ε 逐渐减小时，T 随δ 的变化幅度趋于缓和，尤其在较高水平δ 条件下，T 往往存在一个极值，此值通常称为隔热保温材料最优热工系数。

图1 单层多孔材料热工系数变化曲线

2 温度函数多尺度展开

众所周知，建筑结构保温隔热复材所分布的大量内部孔隙较为随机，但相对于材料尺寸而言，孔隙可视为均匀分布，故孔隙微观尺度的离散性对温度函数的影响忽略不计，因此对于单类均匀材料的孔隙均匀分布时，热工系数可变形为：

基于热桥原理，采用按热工交换方向等分保温层方法优化屋面保温体系温度函数。若将保温层分为纵向n 层，则温度函数可表示为[8-9]：

利用泰勒公式展开，温度函数为：

采用常规保温填充物玻璃棉作为研究对象，基本参数见表1，代入公式（4）绘制其图像，如图2 所示。

表1 常规玻璃棉屋面填充材料设计指标

图2 温度函数与热工材料层数关系

泰勒公式是一个函数在某点的信息描述，若展开项足够多，可认为函数利用泰勒展开后可描述其整个自定义域内的函数信息。但工程数学利用泰勒公式时往往因应用需求而无法考量整个自定义域，即泰勒展开结果无法表征整个函数的信息。因此，公式（3）通过泰勒展开得到公式（4），后者无法获得前者整个自定义域内的函数信息，两者在结果表征上存在偏差。本文考虑工程数学对泰勒展开的约束性质，仅需保障工程精度即可，故对公式（3）进行泰勒展开得到公式（4）可满足精度要求，即此处无需考虑其数学意义。

图2 给出了隔热保温层层数n 与温度函数值之间的关系。由图2 可见，随保温层数n 的增大，玻璃棉保温体系温度系数不断降低，即热交换率不断下降。这表明材料层数越多，保温体系隔热效果越好。但当层数n ＞4，保温体系热工能力逐渐降低，即此时以通过分层方式所优化的材料热工能力很低。因此，对于玻璃棉隔热材料而言，等分4 份能够较好地实现钢屋盖体系较为有效的隔热保温效果。

另外，由于构造层数n 与热工系数U 在n ∈[1，2]区间存在平滑下降段，此时为构造层数渐进式优化实际结果。可以看出，当n 大于4 时，材料热工系数随n 增加的劣化程度逐渐减小，为保障结构合理构造要求下的隔热保温性能，本文推荐n=4 为最优构造设计层数。

3 建筑用玻璃棉保温体系优化试验

3.1 热工试验

为验证本研究所提设计理念的有效性，本文利用试验对比的方法分析相同厚度玻璃棉保温体系在不同层数条件下的热工效果。本实验在西部绿色建筑国家重点实验室开展。首先将试验试样固定于绝温箱窗口，其外表面粘贴热敏传感器，然后通过实现箱内部均化热源实现试样内外温差，见图3。考虑玻璃棉受热变性影响实验效果，热源与试样之间设置挡板。

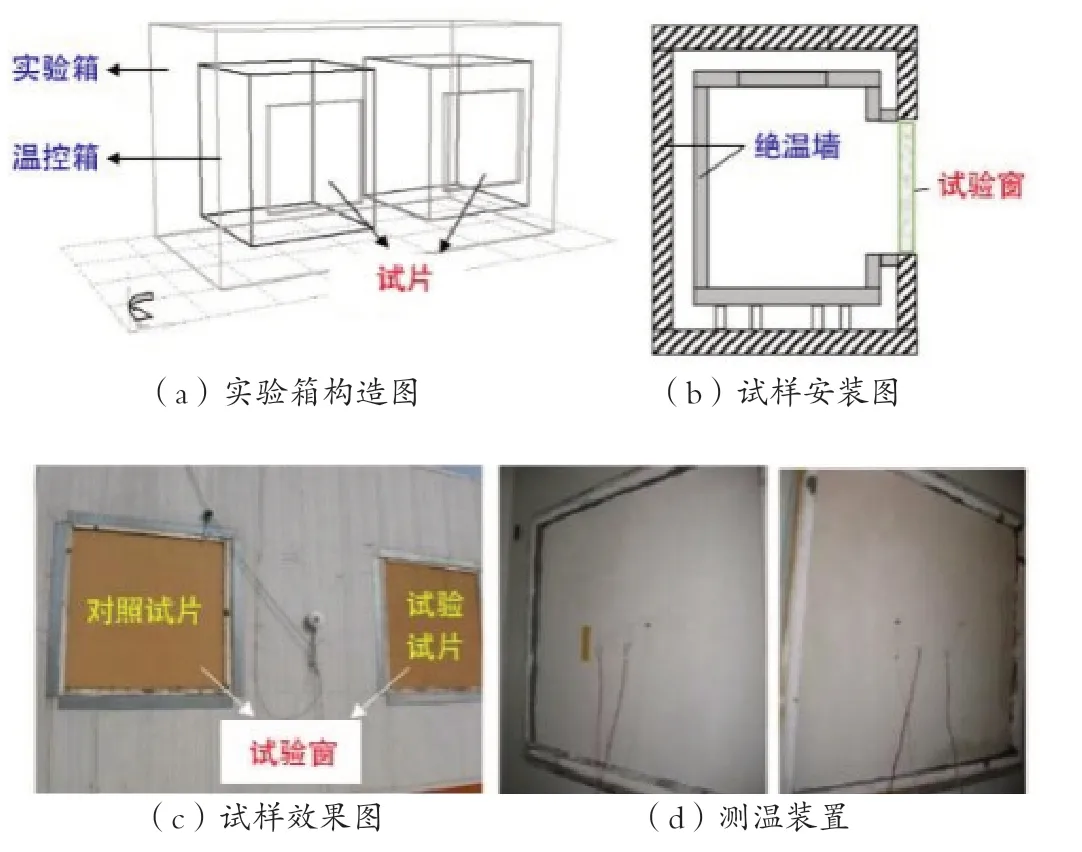
图3 玻璃棉热工试验装置

一般而言，测温装置测量单样本热工效率时，极易受温控环境影响，即非测量样本在场加热过程中极易对测量样本热工计量结果造成影响。因此，为避免环境因素对试验结果造成影响，同批试验设置未安装热源的对比组试验[9]。

根据第2 节理论分析结果，本次实验保温材料厚度取100mm。众所周知，叠合层热工效率与其层数成正比，但层数越多，加工工艺越繁杂，造价成本越高。目前已有研究表明，常规环境下，建筑隔热保温层一般考虑双层构造即可。但对于高原强辐照环境，双层构造一般无法达到需要的隔热保温效果，基于此，本文将叠合层构造增扩至4 层，即保温材料等分层数n 分别取1、2、3、4。

室内辐照试验辐照角度采用正角入射，辐照量范围为200～7 000MJ/m2，并结合拉萨地区近十年平均气温数据，按照全天等效折减施加，24h 为一个周期。试验开始时，辐照装置置于试验装置内中心部位，测试片安装于侧墙设置孔，辐照全过程采用热敏传感器测量其导热数据，并记录于测量软件。需要说明的是，为保障测量数据精度，实验前，安装完试件后，需先对热工装置进行升温预处理。采用装备自带升温系统预加热，持续10min～15min。然后开启热敏装置进行数据读取记录。

3.2 层数对保温体系热工效率影响

一般而言，由于偏斜角因素，太阳辐照量随时间呈指数函数形式下降。而室内试验无法考量偏斜角因素，故试验结果往往与实际条件存在偏差。目前，修正室内试验模拟太阳辐照误差的方法较多，如系数折减法、参量代换法、最小值剔除法以及参变量迭代。前三种方法在计算时将宏观偏差换算为总辐照量百分比，利用各种系数参量进行修正，易于操作，但误差修正效果十分有限。而参变量迭代则是将各时间步计量误差微分处理，结果修正时通过迭代方式对误差进行精确化计量，从而对其修正，因此具有操作效率高、误差控制彻底等优点。

考虑太阳辐照温度随时间的变异性，本实验采用参变量迭代法，对实验热源温度进行周期性调节。不同设计参数试样在热源作用下的外侧温度采集结果如图4 所示。

图4 不同n 条件下保温体系热工测量结果

由图4 可见，随着试验辐照量增加，监控隔热保温层瞬时温度的热敏数据逐渐增加。其中，约夜间22:00～ 3:00 时间，热工效率最低，且叠合层层数越多，热敏最低值越延迟。其原因可解释为由于该时间段辐照量低所致，且隔热保温层数越多，叠合层热工效率越高，因此温度最低点出现的时间越滞后。

另外，虽然该保温体系热工指标随热源温度而改变，但变化幅度均较小，即该体系热工能力良好。同时，随着保温材料层数的增加，其外部测量值逐渐降低，当n 由单层依次增加为4 层，温度传感器测量平均值依次降低7.8%、9.6%、0.4%，即保温层总厚度不变的条件下，随着n 的增加，热工能力增幅逐渐下降，这与理论分析结果一致，说明本文针对建筑钢屋盖隔热保温体系的优化方法具有工程推广与应用价值。