微凸点阵列等效热导率模型及仿真验证

刘云婷，苏梅英，2，李 君，2，曹立强，2

(1. 华进半导体封装先导技术研发中心有限公司基础研发部，江苏 无锡 214135；2. 中国科学院微电子研究所，北京 100029)

1 引言

为适应先进封装对高集成度、高功率密度和小型化的要求[1-4]，一些先进的封装形式得到广泛应用，如扇出型晶圆级封装 (Fan-out wafer level packaging，FOWLP)[5]，3D封装[6]等，先进封装中存在大量微凸点[7]、微铜柱[8]、TSV[9]等结构，以实现高集成度封装结构中的信号互联，这无疑也意味着对热[10]、热-机械[11]等可靠性评估过程对计算成本的极高需求，散热问题成为如今高功率密度集成电路封装设计中亟待突破的技术壁垒之一。目前使用有限元分析(finite element，FE)软件对各种封装形式的器件进行其模型的计算流体动力学(Computation Fluid Dynamics，CFD)仿真，以评估电子产品在其额定功率下工作的散热能力[12]，对封装结构中细小结构进行网格划分和求解计算将会耗费庞大计算成本[13]。

近年来，针对微结构简化研究工作集中在基于3D封装的TSV结构的等效建模，Wang Ningyu[14]基于热等效模型对FOWLP中TSV阵列结构和材料热性能的等效热导系数进行计算和修正，总温升不超过2%的同时节省了80%计算资源；Barabadi B[15]等建立了一种计算效率高、精度高的多尺度降阶瞬态热模拟方法，与传统有限元模型建模仿真的平均绝对误差为7.2%。Pi Yudan[16]对TSV结构进行了热阻网络计算，预测了等效TSV结构的传热能力，温差达到7.5%，网格数减少77%。

目前基于FOWLP热仿真工作，对微凸点阵列结构等效模型相关研究较少，Colombo L[17]基于热阻网络建立了BGA焊球凸点阵列的等效热仿真模型，简化计算的同时可将仿真精度控制在10%；卫三娟[18]采用热阻串/并联方法简化研究了焊点阵列等效，Z方向的温度误差在±1.0%以内，但X-Y方向的温度误差最高接近±30.0%，上述研究虽然在一定程度上保证了计算效率的提升，但仿真精度仍有很大的改善空间。

为在简化计算中提高仿真精度，基于傅里叶定律并修正热阻串、并联方法，建立了三维圆柱凸点阵列模型建立微凸点阵列的等效模型，并对等效凸点阵列模型准确度进行验证；基于自然对流条件，使用JEDEC标准测试板组装FOWLP结构的一款功率放大器，并预测其关键测试点的温度分布，对详细模型和等效模型的温度差、网格数、运算时间进行对比，评估凸点阵列等效模型的工程实用性。

2 微凸点阵列模型等效方法

如图1所示，假设n×n个高密度凸点阵列中每个凸点呈理想圆柱体，由各向同性热导率为KA的均一材料A构成，圆柱底面圆的直径为d，高度为h，相邻凸点间距为2a，各种先进封装结构中，凸点结构周围通常以底填胶包围，以缓解封装内部由于热膨胀系数不匹配而产生的内应力。假定凸点阵列周围填充各向同性热导率为KB的均一材料B。ANSYS ICEPAK软件以四面体网格划分为主，如果在热仿真工作中对每个凸点结构及周围填充物单独建模，大量的细小结构会在网格划分过程中带来庞大的工作量，且圆柱曲面附近的网格质量一般较差，影响求解收敛；为使热仿真过程更加准确、高效，将上述由材料A、B构成的高密度凸点复合结构等效为一个由均一材料构成的立方体结构，长、宽为2na，高为h，如图2。正确求解图2中复合材料纵向及横向热导率，即可根据需求建立由各向异性材料构成的凸点阵列等效模型。

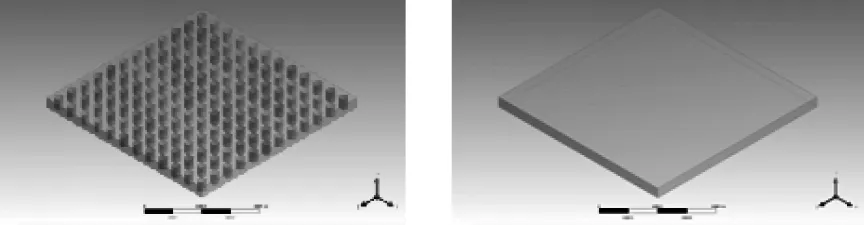
图1 实际模型 图2 等效模型

2.1 求解纵向热导率KY

为简化计算，n×n个凸点阵列中令n=1；等效模型如图3所示，假设热量QY从等效模型的上表面流入，从下表面流出，四个侧面绝热，达到平衡状态后上下表面的温差为ΔTY，SA和SB分别为A和B材料在X/Z平面上的投影面积。

根据傅立叶热传导定律，可推导出Y方向总传热量QY、材料A在纵向的传热量QYA和材料B在纵向的传热量QYB可近似表示为

QY=KY·(SA+SB)·ΔTY/h

(1)

(2)

(3)

其中，SA=π·d2/4，SB=4a2-π·d2/4；忽略对流及辐射散热的影响，则有

QY=QYA+QYB

(4)

将式(4)带入式(1)-式(3)，可以得出等效模型Y方向热导率KY可以由材料A、B的热导率KA、KB及底面积比值α表示，如式(5)所示，其中α=SA/SB。

(5)

图3 求解纵向热导率示意方法

2.2 求解横向热导率KX/Z

由于凸点阵列模型几何对称，X、Z方向等效热导率理论值相等，仅需求解Z方向热导率即可以代表横向热导率KX/Z；将图3模型使用沿过凸点底面圆心点的X/Y面纵切，如图4，则原等效模型可以看成由左右两个材料B组成的部分(部分一)和由材料A、材料B组成的中间部分组成(部分二)，可以得出等效模型横向热导率KX/Z与部分一、部分二的横向热导率KB、KZp2关系如式(6)

5)更新自适应估计转移概率矩阵(transition probability matrix,TPM)。根据文献[10]介绍的方法，在线自适应更新TPM。

(6)

将部分二看成由均一材料构成的，其Z方向热导率为Kp2，将部分二沿X方向切割为无限多个小单元，以底面圆心为原点建立X/Z直角坐标系，如图5，每个细小单元于X方向厚度为Δx；部分二Z向传导的总热量为QZp2，每个小单元Z向传热为QZΔx，则有式(7)

(7)

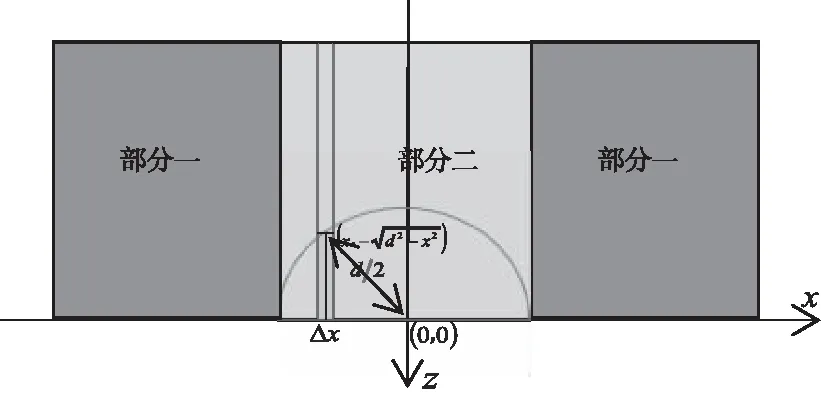
图4 计算等效模型横向热导率示意图

根据傅立叶热传导定律，将部分二、小单元Z方向的热导率KZp2、KZΔx分别代入式(7)，则得出KZp2表达式如式(8)

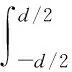
(8)

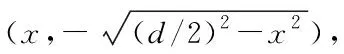
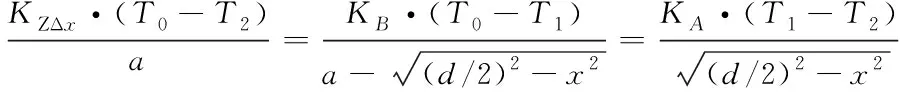
(9)

(10)

将式(10)代入式(8)，求解定积分可以得到部分二横向热导率表达式KZp2为式(11)；其中m、n和p表达式为式(12)-式(14)；将式(11)-式(14)代入式(6)，即可以得到等效模型横向热导率KX/Z。

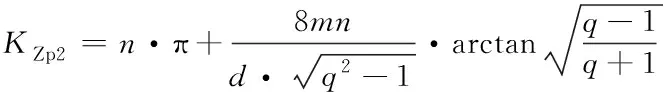
(11)

(12)

(13)

(14)

3 等效模型验证结果

3.1 仿真方法初步验证

使用ANSYS ICEPAK对上述材料热导率等效方法进行验证。如图5所示，首先在尺寸为0.96mm×0.025mm×0.96mm的计算域内建立几何模型，文献[19]和文献[20]为在封装结构中准确验证等效模型的仿真精度，在计算域上表面建立一个热导率极高的缓冲层以保证热流在阵列模型上表面均匀流过，本研究在计算域建立一个功耗0.5W的二维热源，紧贴面热源和底面各建立一个铜材料的导热层，从而使热量较均匀地导入到中间凸点阵列模型中。凸点阵列真实模型如图5(a)所示，12×12微凸点阵列均匀排布，凸点假定为理想的圆柱形状，圆柱凸点Y方向高度为0.04mm，凸点底面直径为0.04mm，相邻凸点间距0.08mm。假定凸点阵列中间四周介质为热导率均一的底填胶，模型结构中各组成部分的尺寸及材料参数如表1所示。

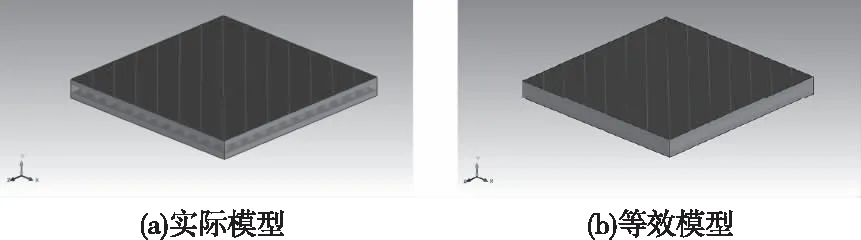
图5 几何模型

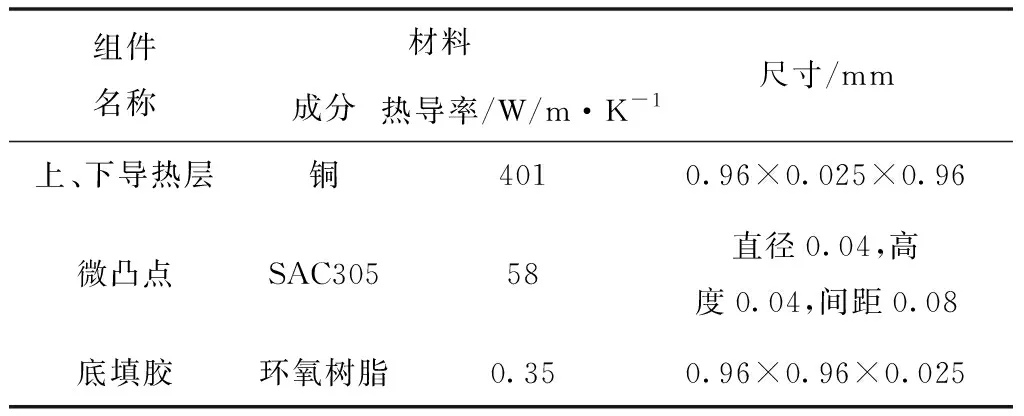
表1 模型结构各组成部分的尺寸及材料参数

凸点阵列等效模型几何建模见图5(b)，使用均一的材料构成的长方体替代图5(a)所示凸点阵列及周围底填胶；并使用上述方法得到图5(b)中等效模型凸点阵列模型的各向异性等效热导率，KY、KX/Z分别为11.6696W·m-1·K-1、0.4703W·m-1·K-1。为保证CFD仿真精度并减少网格数量，采用Mesher-HD方法进行网格划分，对热仿真过程进行边界条件设置。计算域四周及上表面为绝热壁面，底面为温度为20℃的恒温壁面，其余侧面均为绝热界面，真实模型网格数量为66456个，而由于凸点等效模型以一个规则的立方体代替144个凸点阵列及其周围轮廓的底填胶，可降低网格数量至 324个，且等效模型网格的面对齐率、网格偏斜率均高于实际模型。

图6 仿真结果

进行温度分布计算求解至收敛，仿真结果如图6所示，温度最高点均在热源处，最高温度偏差百分比仅为0.728%，节省计算时长92.9%，因此等效模型可以在保证较高计算精度的同时，提升计算效率。

3.2 微凸点直径对仿真结果影响

相邻微凸点间距为0.8mm时，直径分别取值0.02-0.07mm，保持其它组件几何尺寸及各个材料参数不变，进行6个凸点阵列模型详细建模。计算得到等效模型的各向异性等效热导率KY、KX/Z取值，结果见表2。

参考图5所示网格划分方法、边界条件设置及求解设置，分别对不同直径凸点阵列真实模型、等效模型进行仿真求解，将表2中材料热导率输入相应的等效模型，整理网格划分结果及温度仿真结果如表3所示。由表3可知，当相邻凸点间距为0.8mm时，凸点直径在0.02-0.07mm范围内改变时，仿真结果偏差控制在1.659%以下，随着直径减小，凸点侧壁与底填胶接触面间网格划分难度增大，同时当模型其它组件随着凸点直径增大，凸点阵列散热效率提升，模型最高温度降低，与表1结论相吻合。

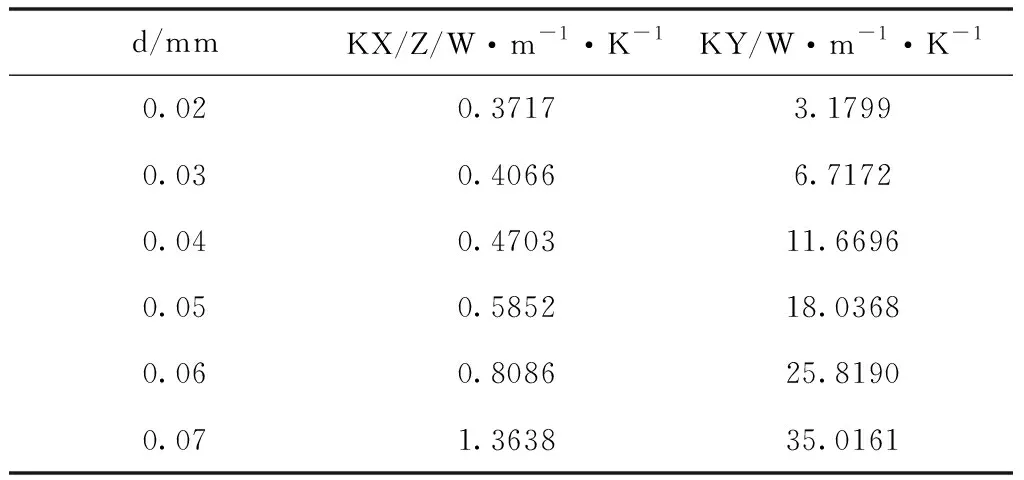
表2 不同凸点直径的等效模型的热导率

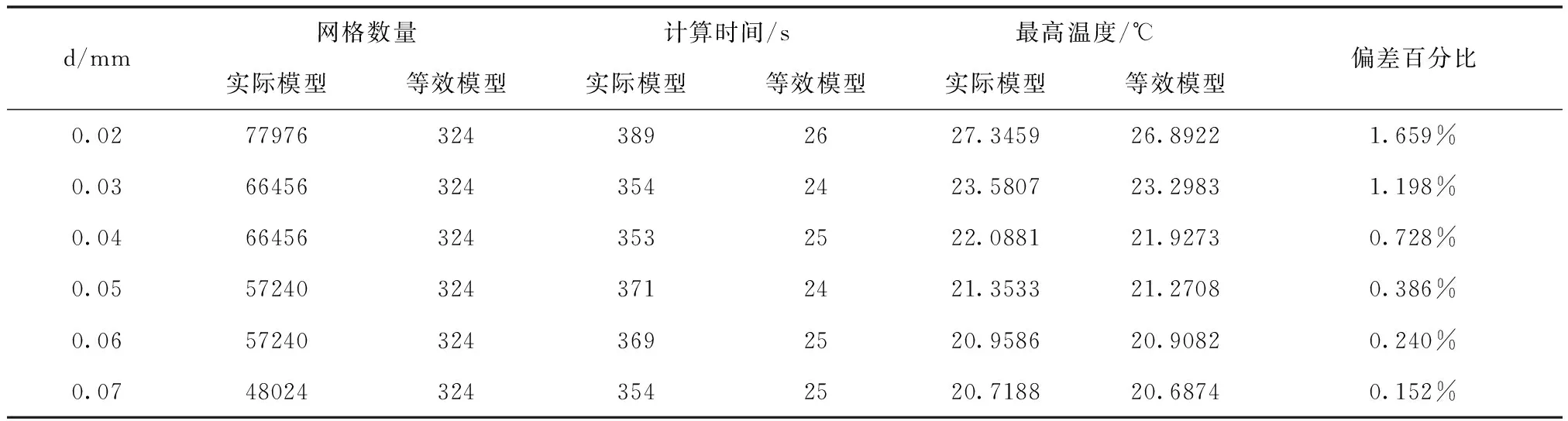
表3 不同凸点直径仿真结果对比

4 微凸点阵列等效模型在先进封装中的运用

评估某款小型Fan-out结构的功率放大器内部热分布，芯片正常工作时功耗为2W，于自然对流下进行热仿真。图7为封装示意图，构件尺寸及材料参数见表4。微凸点间距0.1mm，呈20×15阵列结构排布于芯片下方，并与介质层上表面相连；铜柱阵列排列于芯片外围，间距0.45mm，铜柱上、下表面分别与介质层、UBM层相连，为芯片提供接地通路。

等效模型对实际模型中微凸点及铜柱两个部分进行等效，为简化计算，将两个模型中的BGA球阵列均替换为块体，等效模型尺寸及材料参数见表4。

表4 功率放大器模型尺寸及材料参数

将上述详细模型与等效模型分别封装到JEDEC51-9标准测试板上，分别按照标准规定和封装设计的覆铜率及铜层厚度，使用ANSYS ICEPAK软件中PCB模块建立测试板、介质层的等效模型。

评估环境温度为20℃时，自然对流状态下功率放大器封装结构内部的温度分布，网格划分和求解计算结果见表5，截面温度分布见图8，通过等效简化模型的建立，网格数降低83.15%，计算时间降低72.98%，且仿真精度均可以控制在1.80%以下。

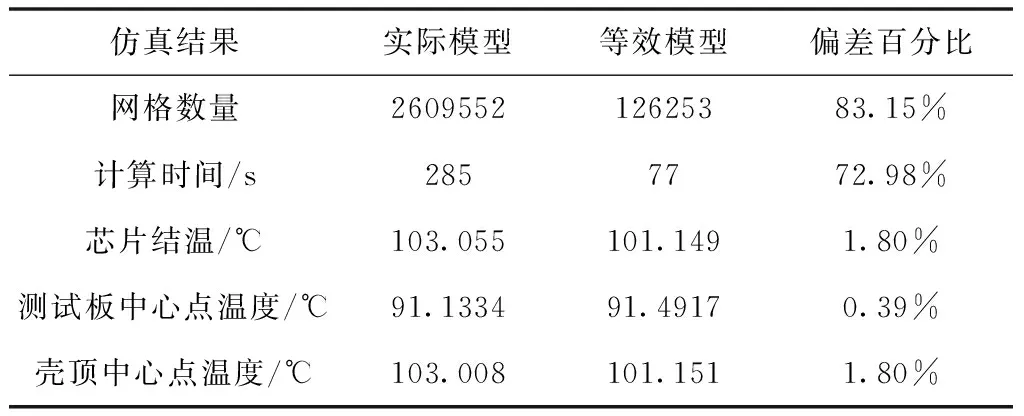
表5 网格划分及仿真结果

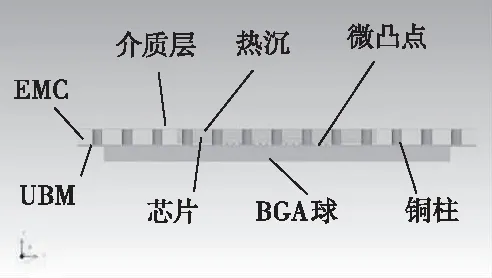
图7 功率放大器结构模型示意图

图8 温度分布

5 结论

对先进封装中微凸点阵列模型进行热仿真等效模型研究，基于傅立叶传热定律，得出了简化模型各向异性热导率与凸点和介质材料的热导率、凸点底面直径及相邻凸点间距的关系，同时研究了凸点阵列不同直径变化对模型导热效率的影响。结果表明，凸点节距为0.04mm时，随着凸点直径由0.02mm增大至0.07mm，模型等效热导率升高，平均网格数降低99.5%，最高温差百分比在1.659%以下，相对于文献[17]、文献[18]的等效方法，本研究提出的等效模型在仿真精度方面有较大提升；在FOWLP结构的功率放大器热仿真中，对微凸点及铜柱结构进行等效替换，等效模型比详细模型计算时间降低72.98%，且两者关键测试点温度偏差均可控制在1.80%以内。研究结果表明，针对微凸点阵列结构的简化建模方法相对常规方式建模求解，最高温度点的偏差百分较低，且提升仿真分析计算效率，具有工程实际意义。