例谈数学史融入教学的有效方法

黄明月

［摘  要］ 将数学史有机渗透在教学中，不仅能让知识的建构更和谐，还能给学生带来探究乐趣，拓宽学生的视野，实现德育教育，为提升数学核心素养奠定基础. 文章以“概率与统计”的教学为例，分别谈谈如何将数学史融入章节起始课教学、概念教学与解题教学.

［关键词］ 数学史；概率与统计；融入方法

数学史是一个巨大的宝藏，蕴含着丰富的知识演进过程、数学思想方法以及科学精神等，它对揭示数学文化，促进人类文明进步具有重要意义. 《普通高中数学课程标准（2017年版2020年修订）》提出：教师应在教学活动中有意识地将数学文化渗透在教学内容中，让学生了解知识的形成历程，充分认识数学知识在科技、社会发展中的作用，以发展学生的人文素养、应用意识与科学精神等［1］.

融入方法

将数学史有机渗透在数学教学中，不仅能让知识的建构更和谐，还能给学生带来探究乐趣，拓宽学生的视野，实现德育教育，为提升数学核心素养奠定基础. 那么，怎样可将数学史融入课堂的各个环节呢？

国外不少学者对这个问题进行了研究，其中Fauvel提出了如下融入方法：①介绍数学家小故事；②借助数学史引入概念；③引导学生分析以概念为答案的数学史问题；④进行数学史课程的讲授；⑤举办以数学史为主题的活动. Arcavi与Tzanakis共同总结出数学史在数学教学中的三种应用方式：①直接提供史料信息；②借助数学史实施教学；③开发社会文化背景［2］. Jankvist提出了模块法、启发法与历史法三种.

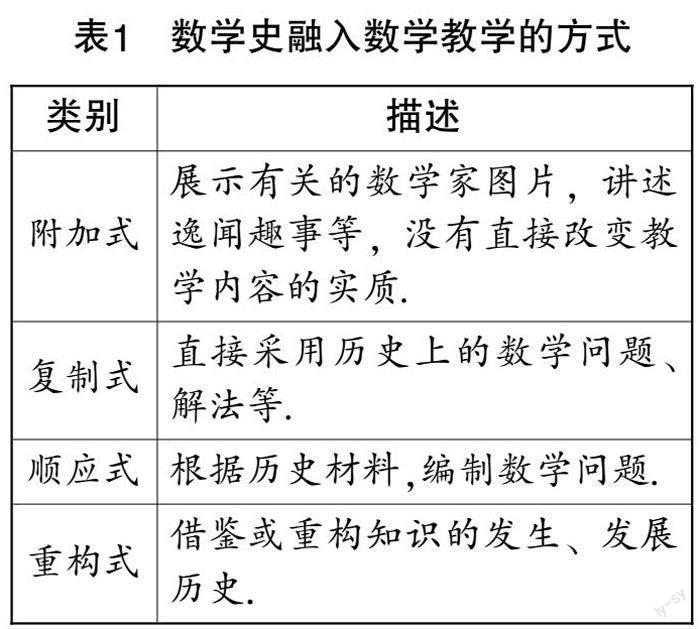
基于以上几种理念，我国学者对在教学中渗透数学史的方法进行了改进与整合，提出复制式、附加式、重构式、顺应式等方法（见表1）. 这为一线教师提供了渗透数学史的方法指导.

融入措施

1. 将数学史融入章节起始课

章节起始课具有统领一个章节的重要作用. 章节起始课的教学，需要让学生明确如下几个问题：我们为什么要学习这部分知识？这部分知识具有怎样的价值？这部分内容的研究思想与方法、历史变迁及发展过程是什么？我们如何学好这部分知识？等等. 教师从这几个问题出发，设计教学目标与计划，能让章节起始课发挥相应的作用.

案例1 章节起始课的教学.

17世纪，梅累向法国著名的数学家帕斯卡提出这样一个问题：我与两个朋友在玩牌时，制定了这样一个规则，即开五局，谁先赢得三局，谁就胜了，赢的人能够获得100法郎. 赛完三局，我赢了两局，一个朋友赢了一局，这时因为不可抗因素导致比赛必须中止，请问我们该怎样分配这100法郎比较公平呢？

这个问题难住了帕斯卡. 在后来的三年中，他与数学家费尔马一起探讨这个问题，最终获得了问题的解决方法. 自此，概率论这个新的数学分支形成了.

该史料风趣、幽默，学生不仅知道了概率论的形成史，还对这部分知识产生了浓厚的探索欲. 如果说概率的起源让学生感到有趣，那么帕斯卡的钻研让学生真真切切地体验到了科学精神. 如今的概率与统计应用十分广泛，普及在生活的方方面面，谁也没想到它的由来竟然跟一场赌博有关.

由上可知，将数学史融入章节起始课，可激发学生对知识的探索欲，让学生明确这部分知识的学习价值与意义是什么，也为学生形成正向的数学观与人生观奠定基础.

2. 将数学史融入概念教学

概念是数学的基石. 每个数学概念的形成都经历了漫长的历史过程，然而有些教师在教学中“重解题，轻概念”，这种行为严重阻碍着学生基础知识与技能的发展. 想要让学生学好数学这门学科，首先就要让学生明确各个概念的内涵与外延.

在“概率与统计”章节中，有不少概念都源于生活实际中的实物模型或问题，有些概念的形成与发展经历过不少挫折，教师若将这些史料展示给学生，会让学生充分感到每一个概念的来之不易，从而激发学习兴趣，启动数学思维. 事实证明，结合数学史进行概念教学，可让学生领略到知识的发展历程，在概念的来龙去脉的探索中理解知识本质，为新知的建构服务.

案例2 “正态分布”的教学.

在生活中，我们常会做一些测量活动，如果测量工具的精准度不够，那么误差就会偏大. 为了减小误差，一般会选择多次测量来获取更多的数据，便于提高数据的预估值. 鉴于测量误差存在较大的随机性特征，数学家高斯在1809年提出用“正态分布”来刻画测量的误差. 因此，人们也称正态分布为高斯分布，由于它的形状类似于钟，又被称为“钟形曲线”.

正态分布反映了一种极其普遍的现象，多数情况下以“两头低、中间高”的形态呈现. 其实，生活中有很多看似毫无规律可言的数据，比如人的身高、体重，大批量产品的质量，等等，都具有正态分布的特点，这也体现了纷乱中的秩序性特征.

为了纪念高斯在这方面所作出的贡献，德国10马克的钱币上不仅印有高斯的頭像，还将正态曲线印制在上面.

高斯与正态分布的故事成功吸引了学生的注意力，让学生对正态分布的起源、发展等有了明确的认识，从而对这个概念产生了莫名的亲近感. 一部分学生课后还特地搜索德国10马克的纸币来观察，拓展知识面的同时促进了思维的发展.

3. 将数学史融入习题教学

从数学史本身来说，它就是一个巨大的问题库，我们所熟悉的勾股定理在各个文明古国的数学文献中都载有与之相关的问题，教师授课时可结合学情从中择取应用. 如《九章算术》中就有这样一句话：“今有池方一丈，葭生其中央，出水一尺. 引葭赴岸，适与岸齐. 问水深葭长各几何？”

教师将此类问题应用在教学中，一方面能培养学生的抽象能力，另一方面能激发学生的想象力，让学生感知“数学源于生活且服务于生活”的理念. 同时充分感到我们当前所接触到的定理、规律、法则等都是数学家经过思考、创新、总结而来的.

案例3 “圆周率π”的求解.

与圆周率π相关的数学史料比较丰富，其中不乏一些很有创意的求解方法，比如“布丰投针实验”：“在18世纪，数学家布丰提出一个问题：假设一块地板上的木纹平行且等距，在这块地板上随意抛一根长度小于木纹距离的针，这根针与其中一条木纹相交的概率是多少？”

布丰提出的这个“随机投针实验”，是估算圆周率π的重要方法之一——历史上不少人用这个方法估算出圆周率在3.14左右. 该实验的价值并不在于获得了π的近似值，而是强化用几何法求概率. “布丰投针实验”开创了用随机数据处理确定性问题的先河，属于用偶然性方法解决确定性问题的鼻祖.

受上述数学史的启发，教师可要求每一个学生随机写一个正实数对（x，y）（x，y都是小于1的正实数），统计x，y两数能够和1构成钝角三角形的数对个数m，而后根据m估算π的近似值.

总之，借助数学史渗透数学文化，提升学生的数学核心素养是新课改的必然趋势，也是值得每一个教师都关注的主题. 将数学史有机融入“概率与统计”的教学，可让学生充分领略“概率与统计”相关知识形成与发展的过程，实现知识的“再发现”，帮助学生建构完整的知识体系，提升学生的人格品质.

参考文献：

［1］ 中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［S］. 北京：人民教育出版社，2020.

［2］ 吴文俊，沈康身. 中国数学史大系·第二卷［M］. 北京：北京师范大学出版社，1998.