习题设计：用“发展”代替“重复”

姜华

摘要：观察《解决问题的策略——转化》第2课时的教学，发现学生在变式练习中遭遇滑铁卢。分析发现，巩固应用环节的习题设计，存在简单重复的问题。对此，提出用“发展”代替“重复”的改进思路。具体包括：以“熟”解“生”，夯实基础；消除定式，深化理解；打通联系，整体架构。

关键词：小学数学；习题设计；解决问题的策略

一、缘起：学生在变式练习中遭遇滑铁卢

苏教版小学数学五年级下册《解决问题的策略——转化》单元，主要教学内容为用转化的策略解决相关的问题。转化是一种常见的、极其重要的策略。理解并掌握这一策略，对于学生形成分析问题、解决问题的能力以及发展数学思维能力，都具有非常重要的意义。转化策略教学的难点在于引导学生针对具体问题寻找合适的转化方法。

前段时间，学校举行了青年教师赛课活动，其中一位教师执教的就是《解决问题的策略——转化》第2课时，教学内容主要为例2（计算“1/2+1/4+1/8+1/16”）及相关习题。例2从数与运算的角度编排了连加式题的等值转化，旨在先让学生各自计算一组公比为12的等比数列的和，再引导他们借助直观图形将这组分数连加计算转化为相对简单的分数减法计算。该教师设计的教学流程是：先让学生说说例题中的算式有什么特点，启发学生从不同的角度表达发现；然后要求学生各自计算，再相机揭示数形结合的转化方法，即把正方形看作单位“1”；在巩固应用环节，选用了3道习题（见下页图1），学生基本能基于例题学习时获得的经验，继续运用转化策略，借助直观图形顺利解决问题，甚至有学生能在看到题目后将答案脱口而出。学生似乎已经掌握了转化策略的应用过程和特点，形成了运用转化策略解决问题的能力。

但后续的当堂检测环节，学生在解答变式练习“1/3+1/6+1/12+1/24+1/48”时却遭遇了滑铁卢。学生的解题过程主要有两种（见图2、图3）。从图2中的解题过程可以看出，从例题到巩固练习再到这里的变式，学生出现了思维定式，直接套用了例题中的转化结论。图3中，学生采用了将“异分母分数通分成同分母分数”的一般分数计算方法，过程相对比较复杂。对此类学生进行访谈得知：他们通过对比发现，该题中的分数与之前多道练习中的分数都不一样，不再是“1/2，1/4，1/8，…”，感觉之前的方法不再适用，所以采用了最稳妥的通分法。

全班37名学生中，能自觉将这个分数连加计算转化为相对简单的分数减法计算并计算正确的只有3人，约占总人数的8%，此前出现的令人欣喜的教学效果不复存在。这自然引起了我们的关注：问题到底出在哪里？

二、分析与改进：习题设计应该用“发展”代替“重复”

我们知道，习题是对例题的重要补充，能够帮助学生巩固基础，助力学生将知识点串成线、织成面。而上述教师的习题设计，存在简单重复的问题。

教材编排的例2中，4个分数的分母依次是2、2×2、2×2×2、2×2×2×2，后一个分数的分母总是前一个分数分母的2倍，也就是说后一个分数的值总是前一个分数的一半，这是一组公比为1/2的等比数列。图1中的三道巩固习题看似分层有序，实则思维层次比较接近：虽然分数的个数在例2的基础上有所增加，但分数的形式、结构都沿用了例2的。学生完全可以套用例2中获得的方法解答三道题，这属于机械模仿的重复训练。学生的思维水平并没有拾级而上，仍在浅层原地踏步。这使学生多次获得了成功套用的体验，例2中的转化结论深入其心，导致思维定式。

郑毓信教授指出：对同一类型的问题，教学中我们也应很好地体现这样一个重要原则——“用发展代替重复”，也即应当特别重视认识的必要深化，而不应简单地进行重复。［1］

筆者以为，这三道习题可以这样改进：

1.请根据下页图4—图6的涂色部分，分别列出三道分数加法算式，并计算结果。对比三个算式，你有什么新的发现？（正方形表示“1”）

2.计算1/3+1/9+1/27+1/81。

3.我们通过画图研究了“1/2问题”“1/3问题”，你还想研究“1/（）问题”？通过研究，你发现了什么？

第1题，以“熟”解“生”。

本节课中，例题的教学让学生初步感知可以借助直观图形将复杂的加法算式转化为简单的减法算式，这属于对策略的浅层感知。于是，在此基础上逆向设计三道“由图到式”的形似习题。说其形似，是因为三幅图的涂色部分所对应的加法算式，都是公比为12的等比数列的和（简称“1/2问题”），而且图形的整体结构相似，但与例题图相比，同中有异，异中有深化。

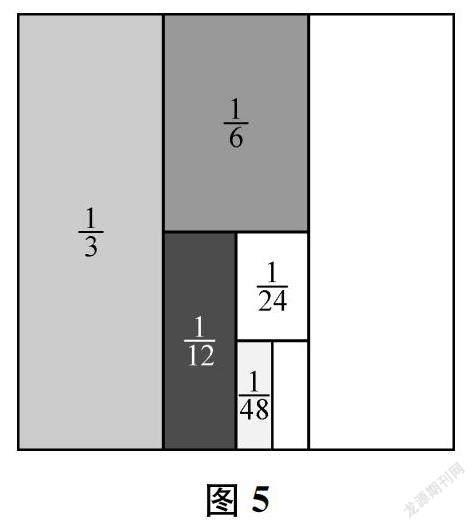
图4与例题的图最为相似，只是分数个数的差别，旨在引导学生巩固例题中初步获得的转化经验：首项为1/2的这一列等比分数的和，都等于1减去加数中的最后一个单位分数；随着分数的增多，结果越来越接近1。图5与图4及例题图相比，首项不再从1/2出发，打破了之前的认知平衡，给了学生一个全新而有力的冲击，使他们意识到这样的转化策略不是只能运用于求首项为1/2的一列等比分数的和，还可以做进一步拓展。转化的策略是相通的，但是转化后的算法是有变化的，不再用1来减，而是用2/3减去加数中的最后一个单位分数。图6的出现是为了引导学生进一步提炼“1/2问题”的转化规律。

三张图、三个算式，依托同一情境，有层次地呈现有变化的问题，旨在引导学生在例题学习的基础上拾级而上。前一算式的熟悉、熟练为后一算式的解答储备知识和经验，后一算式又会在前一算式的基础上生长出新的变化，引发新的思考，从而帮助学生提升转化策略的认知层次。

第2题，消除定式。

学生在第1题的解决中，已经建立了“1/2问题”的解答模型，“1/3+1/9+1/27+1/81”的出现，旨在消除“1/2问题”的思维定式，向更广、更深处延伸。由于“1/2问题”的解答模型的影响，多数学生看到第2题的第一反应就是转化成“2/3－1/81”。在用常见的通分方法验证后，发现这样转化的结果并不正确。此时，学生自然会产生疑惑，想到用画图来验证。在初次画图时，几乎所有的学生都沿用了“1/2问题”中的图形结构（见图7），发现1/3+1/9+1/27+1/81应转化成2/3－2/81－1/27－1/9，所以2/3－1/81的转化结果是错误的。此时依图而来的转化，并没有让问题的解决得到简化。不成功的转化经历，迫使学生回到起点重新去观察这一组分数的特点，从而发现这是一类新的问题（简称“1/3问题”），需要进一步探究适用于其的画图方法（见图8），并在此基础上探寻有别于“1/2问题”的转化过程。

由基础的“1/2问题”延伸到变式的“1/3问题”，学生把画图这一方法用到了深处、实处。他们在画图中对比，在画图中突破，在一次次看似失败的经历中，数学思维却在向纵深拓展。学生通过类比、探究，不仅明晰了不能机械模仿的道理，也在多变的现象中完善了认知结构，达成了对策略的深度理解。

第3题，打通联系。

从形似习题到变式习题，学生打开了思维的闸门，跳出了教材的局限，不仅画图研究了“1/2问题”，还拓展研究了“1/3问题”，学生的视野更广阔了。此时，大部分学生对“1/（  ）问题”的研究印象是“各有各的转化策略”，彼此之间是割裂的。第3题，意在给学生一个更广阔的研究空间，从一道题的研究走向一系列问题的研究，打通学生对“1/（  ）问题”初步形成的转化策略的“隔断墙”。通过研究，学生自然会发现：当a为大于等于2的自然数时，求关于几分之一的等比数列的和是有通法的，也就是有相通的转化策略的，即1a+1a2+1a3+…+1an=1-1an÷（a-1）。当然，实际教学中有时不会这么深入，不需要学生得到这一公式。

这凸显了知识的结构化与一致性，也让转化的策略得到了充分的延展。

参考文献：

［1］ 郑毓信.数学深度教学的理论与实践［M］.南京：江苏凤凰教育出版社，2020：120.