基于数学抽象素养的教学设计
——以“空间向量及其运算(1)”为例
2023-03-27江苏省邗江中学王瑞丁
⦿江苏省邗江中学 王瑞丁
1 学情及目标分析
1.1 学情分析
学生在必修二中已经学习了平面向量的相关概念及运算,但对于如何使用已知的一组基底表示平面内的任意向量往往会有畏难情绪和思维障碍[1],所以本节课要充分发挥教师的主导作用,特别是在证明四点共面的问题上,教师在引导的过程中,要让学生多参与、多思考、多交流,从而培养他们分析和解决问题的能力,为学生的可持续发展和终身学习创造条件.
1.2 目标分析
(1)理解空间向量的相关定义,掌握空间向量的线性运算(重点).
(2)理解方向向量和共面向量的定义,通过类比平面向量共线的充要条件及平面向量基本定理,探究空间向量共线及共面的充要条件(难点).
(3)掌握空间中的“共线向量定理”及其应用(重点).
2 教学过程
2.1 创设情境,提出问题
春节期间,小明游览广州白云山(O)后,乘坐地铁到花城广场(A)观赏珠江,然后抵达广州塔(B)游玩,如图1,小明的实际位移是什么?什么数学概念可以用来表示其位移过程?

图1
小明如果还要登上广州塔顶端(D)俯瞰广州漂亮的景色,如图2所示,那其实际位移是什么?该怎样表示这个过程呢?
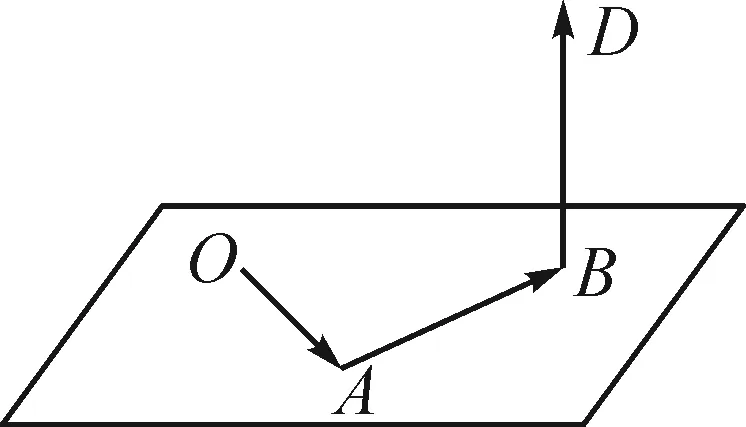
图2
设计意图:情境导入通过展示广州白云山及珠江的图片,激发学生的学习兴趣和求知欲,既缩短了数学与生活的距离,又增强了民族自豪感.同时,教师引导学生通过平面向量知识类比学习空间向量,激发了学生的学习兴趣,为后续空间向量的加减法运算作铺垫.
2.2 类比探究,揭示规律
思考1:基本概念的类比
平面向量中我们学习过哪些基本概念?类比平面向量所学的基本概念,是否同样可以得到空间向量的基本概念?
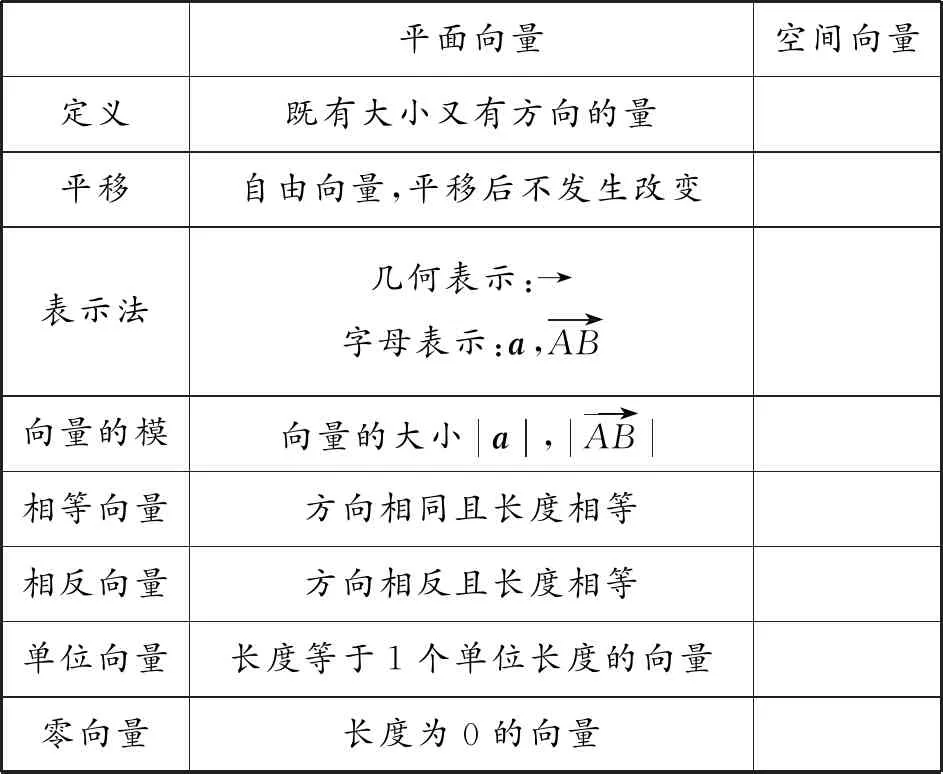
平面向量空间向量定义既有大小又有方向的量平移自由向量,平移后不发生改变表示法几何表示:→字母表示:a,AB→向量的模向量的大小a,AB→相等向量方向相同且长度相等相反向量方向相反且长度相等单位向量长度等于1个单位长度的向量零向量长度为0的向量
思考2:线性运算法则的类比
在平面向量中,我们学习了哪些运算法则?在空间向量中,这些运算法则是否适用?

平面向量空间向量加法运算三角形法则或平行四边形法则减法运算三角形法则数乘运算ka(k为正数、负数、零)
思考3:运算律的类比
前面我们学习了平面向量的哪些运算律?这些平面向量的运算律在空间向量中是否成立?

平面向量空间向量加法交换律a+b=b+a加法结合律(a+b)+c=a+(b)+c向量和实数的加法分配律λ(a+b)=λa+λb(λ1+λ2)a=λ1a+λ2a
思考4:共线向量的类比
在平面向量中,我们学习了共线向量,那么对于空间向量,结论是否仍然成立?
探究1对任意两个空间向量a,b,如果a=λb(λ∈R),a与b有什么位置关系?反过来,a与b有什么位置关系时,a=λb?
探究2对平面内任意两个不共线向量a,b,由平面向量基本定理可知,这个平面的任意一个向量p可以写成p=xa+yb,其中(x,y)是唯一确定的有序实数对.对两个不共线的空间向量a,b,如果p=xa+yb,那么向量p与向量a,b有什么位置关系?反过来,向量p与向量a,b有什么位置关系时,p=xa+yb?
设计意图:对于平面向量的知识脉络,学生掌握得比较透彻,空间向量的知识体系与其具有高度的相似性,让学生自己去阅读、比较、辨别、思悟,从平面向量到空间向量,从二维到三维,体会概念的类比过程.通过深入类比,学生的思维逐步过渡到空间向量;通过概念辨析,加深学生对向量内涵与外延的理解,突破重难点;通过归纳知识点和方法,培养学生数学类比、归类、整理意识.
2.3 典型剖析,巩固提升
例1在正方体ABCD-A′B′C′D′中:

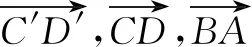
例2已知平行六面体ABCD-A′B′C′D′,化简下列各式:
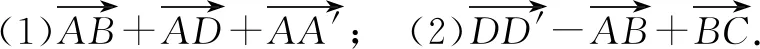

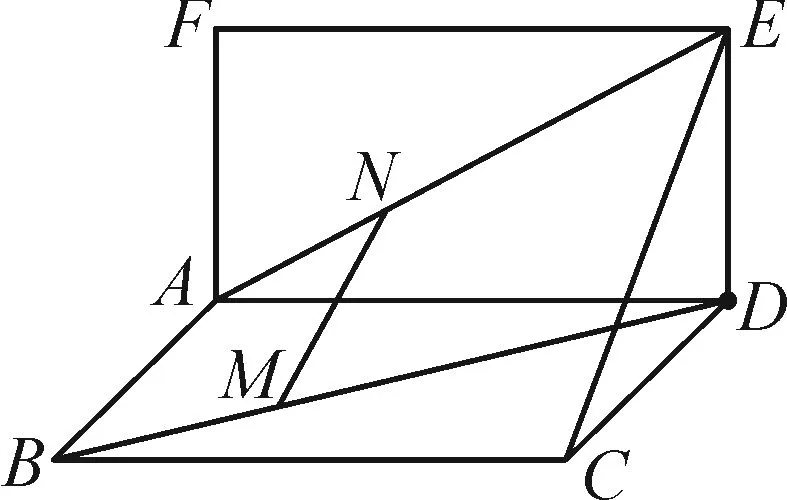
图3
设计意图:引导学生应用所学知识解题,通过例题巩固、理解空间向量基本概念,会用线性运算法则、共线定理解决实际问题.进一步让学生体会空间向量在解决立体几何问题中的应用,提升推理论证能力,提高学生的数学运算及逻辑推理核心素养.
2.4 反思回顾,自主总结
(1)空间向量的基本概念.(2)空间向量的线性运算法则及运算律.(3)运算律.(4)共线向量:①定义;②方向向量;③共线定理.
结论1:空间任意两个向量都可以平移到同一个平面内,成为同一个平面内的两个向量.
结论2:三个不共面的向量的和等于以这三个向量为邻边的平行六面体的体对角线所表示的向量.
设计意图:系统梳理整节课所学内容.
2.5 课后作业
(1)(多选)下列命题,错误的是( ).
A.若a≠b,则|a|≠|b|
B.若|a|>|b|,则a>b
C.若a=b,则||a|=|b|
D.若|a|=|b|,则a=b或a=-b

设计意图:通过练习巩固本节课所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、数学建模等核心素养.
3 小结
教育心理学家奥苏伯尔曾说过:“影响学生唯一最重要的因素,就是学习者已经知道了什么.”[2]
本节课教师引导学生回忆平面向量的基本知识,在回忆旧知识的过程中,学生通过自行类比探究空间向量的新概念与知识;而在解决例题的过程中,学生需要使用线性运算法则、共线定理等,符合学生认知能力的发展顺序.因此,本教学设计立足于学生已有的认知结构,通过引导学生经历观察、思考、合作、探究、交流的过程,螺旋式培养学生的数学抽象和直观想象等核心素养.
