教材中一道经典抛物线问题的赏析

⦿昆山市柏庐高级中学 王会平

教材上的例、习题大多是经典的好题，凝聚了教材编写专家的心血和智慧，有着丰富的内涵和可拓展的外延，它对教学的影响是深刻的.充分理解这部分的例、习题，研究其解法以及其在教材中所呈现的价值，对学生后续的学习和教师进一步的教学也是很有意义的.好题如歌，让人乐不思蜀；好题如诗，令人回味无穷；好题如工艺品，叫人爱不释手；好解又如画笔，犹有画龙点睛之功效.下面结合教材中一道抛物线习题，进行解法分析，与读者共赏.

1 题目呈现

如图1，M是抛物线y2=4x上一点，F是抛物线的焦点，以Fx为始边，FM为终边的∠xFM=60°，求|FM|.

图1

2 解法欣赏

2.1 雅俗共赏、似曾相识

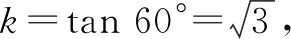
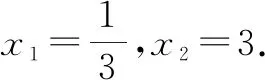
方程两边平方，整理得3x2-10x+3=0.

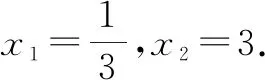
故|FM|=2|FA|=2(x2-1)=2(3-1)=4.

以上两种解法为解析法，只需求M，F两点的坐标，再求出距离即可，目标明确，易于操作，有似曾相识之感.

2.2 构思巧妙、超凡脱俗

解法三：抛物线y2=4x的焦点F(1,0)，准线l：x=-1,l交x轴于点B,过点M作MQ⊥l，垂足为Q，过点F作FH⊥MQ于点H，如图2.

图2

由|MF|=|MQ|，∠QMF=∠xFM=60°，可知△MFQ为正三角形.

故|FM|=|MQ|=2|QH|=2|BF|=4.

该解法立意新颖，一反常规求两点间距离的方法，而是根据图形特征所呈现出题目的条件及其数量之间的关系，寻找解决问题的捷径，把数学中的合情推理和逻辑推理有机结合在一起，用平面几何的方法求解问题，思路简洁，构思巧妙、超凡脱俗.

2.3 旧貌新颜、焕发青春

由M是抛物线y2=4x上一点，可得

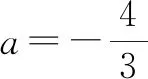
故|FM|=4.

该解法并非直接通过求点M，F的坐标来求|FM|，而是成功地改造了点M.通过逆向思维，假设|FM|为a，利用直角三角形中边角的数量关系，获得点M的坐标，再利用点M在抛物线y2=4x上求解a，旧貌新颜、焕发青春，简洁而又直观.

2.4 思维发散、力度颇深

解法五：由题意知点M在第一象限，设点M坐标为(m,n)，其中n>0.

由抛物线的方程为y2=4x，得其焦点F的坐标为(1,0)，准线方程为x=-1.

所以，由抛物线定义，可知|FM|=m+1.

过点M作MA垂直x轴于点A，则|FA|=m-1.

解得m=3.

故|FM|=m+1=4.

该解法对数学思维能力的要求比较高，具有一定的发散性，要求对抛物线的定义、几何图形的性质透彻理解，恰当运用，解题能力可谓深入浅出，力度颇深.

3 类比探究

3.1 同题异构、推陈出新

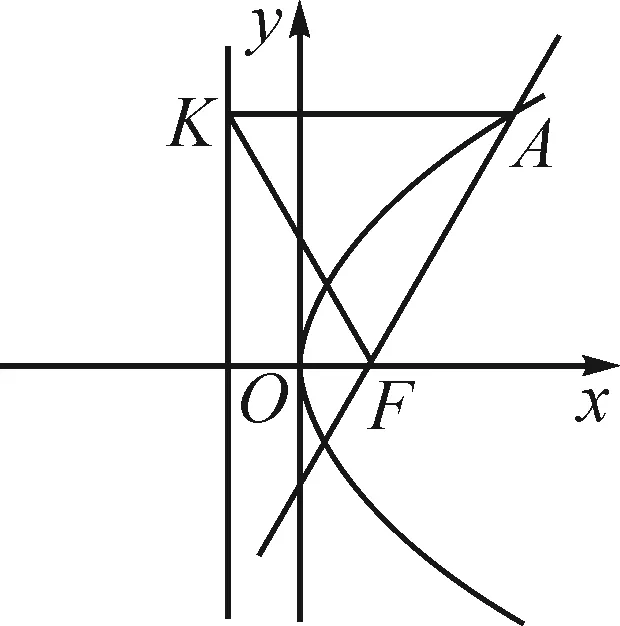
图3

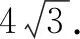
3.2 以静制动、量质飞跃

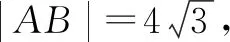
图4

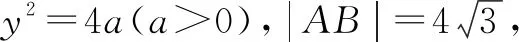
3.3 巧变多考、匠心独创

(Ⅰ)当k=0时，分别求C在点M和N处的切线方程；

(Ⅱ)y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

分析：该题虽然仍是直线与抛物线相交的问题，但是题目却巧妙地与二次函数、一次函数接轨，既考查了函数与导数的问题，也考查了直线与抛物线的问题，是一次成功的变式.前面例2考查的是直线平移变换，而本题考查的却是斜率的变化，的确是巧变多考、匠心独创.

对于第(Ⅱ)问，先作出判定，再利用设而不求的思想进行求解.将y=kx+a代入曲线C的方程整理成关于x的一元二次方程，设出点M,N的坐标和点P的坐标，利用设而不求思想，将直线PM，PN的斜率之和用参数a表示出来，再利用直线PM，PN的斜率之和为0，即可求出a,b的一个关系，从而找出适合条件的点P坐标(0，-a).本题有效考查了抛物线的切线、直线与抛物线的位置关系等知识，同时也对学生探索新问题以及运算求解能力进行了考查.

总之，通过一个对问题深入、多层次的研究，我们能从经典题的解法和随之而来的问题生成中感受到数学的奥妙，同时也从解法的生成性研究中找到教与学的乐趣.以上三个例题是对抛物线生成性问题的类比研究，通过知识的类比探究，由低向高，逐层提升.