情境设计：小数数学“问题提出”教学的有效策略

周夏

摘 要：小学数学“问题提出”的教学与情境设计两者之间存在着密切的联系.《义务教育数学课程标准（2022年版）》中明确指出“情境设计”与“问题提出”在逐步发展学生核心素養中起着重要的作用.本文阐述在小数数学“问题提出”教学中，以情境设计为策略，为学生提供适切的提问背景，让学生有问题可提、敢提、想提和乐提，逐步进行深度学习，使数学核心素养得到更好的发展.

关键词：情境设计;问题提出;核心素养;深度学习

《义务教育数学课程标准（2022年版）》的总目标中指出“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，在探索真实情境所蕴含的关系中，发现问题和提出问题，运用数学和其他学科的知识和方法分析问题和解决问题”^［1］.这也指明了培养“会用数学的思维思考现实世界”这一方面的核心素养.总目标明确提到情境与提出问题，同时，在不同学段中也分别对“问题提出”做了具体目标要求：第一学段（1～2年级）：学生借助教师的指导，在日常生活的情境中提出简单的数学问题；第二学段（3～4年级）：学生能在日常生活的情境中自主尝试发现和提出数学问题；第三学段（5～6年级）：在真实的情境中，学生能尝试发现和提出问题.

可见，问题提出已然成为数学教学改革关注的新焦点^［2］.小数数学“问题提出”教学是指在相关数学知识内容的教学中，学生在已有的认知和经验基础上，对具体的情境做出自己的理解，并建构有意义的数学问题的过程.在这样的过程中，“问题提出”教学离不开情境设计.在不同学段、不同环境、不同内容、不同环节设计适切的教学情境，能激发学生主动提问的动机，让学生逐步具备“问题提出”的意识，不断提高“问题提出”的能力，进而能让学生学会有效提问，不断走向学习深处，让“问题提出”教学不断走向深度学习的教学，同时也是发展学生核心素养的数学教学.

1 设计生活情境：让学生有问题可提

著名物理学家李政道教授赠江苏省木渎高级中学的题词为“求学问，需学问，只学答，非学问”.创造一个善于思考、鼓励思考的环境是相当的重要的，只有在这样的环境、情境中，学生才会真正有问题可提.

要想学生有问题可提，在教学中需要引发学生思考，因为在思考中会产生疑惑，而疑惑便是问题的源头.常说数学来源于生活，结合新课标在不同学段中对“问题提出”做出的具体目标要求，容易想到，在数学教学过程中，设计有效的生活情境，可以让学生有问题可提，在长期的思考与提问中，也便能形成问题意识.

例如，在教学《认识年、月、日》这一课时，虽然新课知识点比较多且散，但这些知识和生活密切相关.在教学时，可以设计相关的生活情境，让学生准备好近几年的年历卡（含2020年），通过观察比较，提出自己疑惑方面的问题，在这过程中学生便有了“为什么2月有时28天，有时29天？为什么人们要分大月、小月？为什么有的年份一年是365天，有的是366天？”等问题.

这些都是学生结合自身生活环境催生出的问题，同样也是学生内在需求的“问题提出”.学生长期在这样的过程中学习数学，也便有了数学问题可提，进而不断激发问题提出的欲望，让学习走向更深处.

2 设计真实情境：让学生有问题敢提

在日常教学中，不难发现有的学生很善问，也有的学生不愿意提问，这主要取决于他们长期处于怎样的学习情境中.如果学生的认知能力不能融入相关情境，达不到同频共振的效果，便会抑制学生的提问意识，从而不敢提出问题.然而，从心理学角度看来，当人们面临一项任务而又没有直接手段去完成时，就有了“问题”^［3］.可见，教师在教学过程中更要关注不敢提问题的学生，抓住时机鼓励、引导他们，消除他们的心理负担，让他们感受到提问的快乐，从而喜欢上提问.在真实的情境中，更能催发学生的提问动机.设计真实情境，能让更多的学生有问题敢提.

例如，《三角形的三边关系》这一课时中，探索三角形的三边关系实际是前面学习知识点的延续，教学时可以从三角形三个点之间的特殊关系开始，从而有效地引导学生探索三角形三条边之间的特殊关系.让学生回顾三角形有什么特征，自然地引出三个顶点、三条边和三个角，进而回顾用三个点作为顶点围一个三角形，不能在一条直线上这一特殊规定.在这样的真实情境中，学生便敢于提出：既然三角形的三个顶点有这样的特殊规定，那么三角形的三个角之间有什么特殊的关系？三条边有什么特殊规定呢？……有了这样既精准又有价值的问题，学生的新知学习便有了目标与方向.

在这真实的情境中，不仅能引导学生学会思考，更能鼓励学生敢于提问.教师通过适当地表扬与鼓励，还能树立学生敢于提问的信心.

3 设计数学情境：让学生有问题想提

当学生敢于提出问题了，也便会有想要提出问题的冲动.教育家波利亚曾经说过，“教师的作用在于系统地给学生发现事物的机会，并给予恰当的帮助，让学生在情景中亲自去发现尽可能多的东西.”结合小学数学“问题提出”教学来看，设计适当的数学情境，能促使学生有问题想提.

例如，在教学五年级上册第二单元《多边形的面积》中，《同步练习》上有这样一道拓展提高题：有一张正方形纸，边长是62厘米，要把它剪成两条直角边分别为6厘米、5厘米的直角三角形小旗（不能剪拼），最多可以剪多少面？

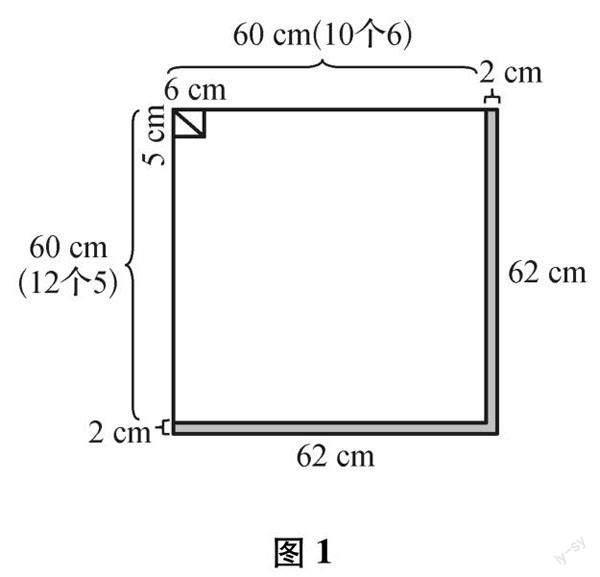
因为是“裁剪”问题，且不能剪拼，所以本题不适合用正方形纸整体面积除以每个直角三角形小旗的面积来解决，而适合先把两个完全一样的直角三角形小旗合成一个长方形后，考虑正方形纸的相邻两条边长里面可以分别剪成多少个小长方形的长和宽后再来解决.因此，绝大部分学生会有这样的解答过程，62÷6＝10（个）……2厘米，62÷5＝12（个）……2厘米，12×10×2=240（面）.这样的解答思路，如果没有想要提出问题的学生，或许连老师自己也就默认了.

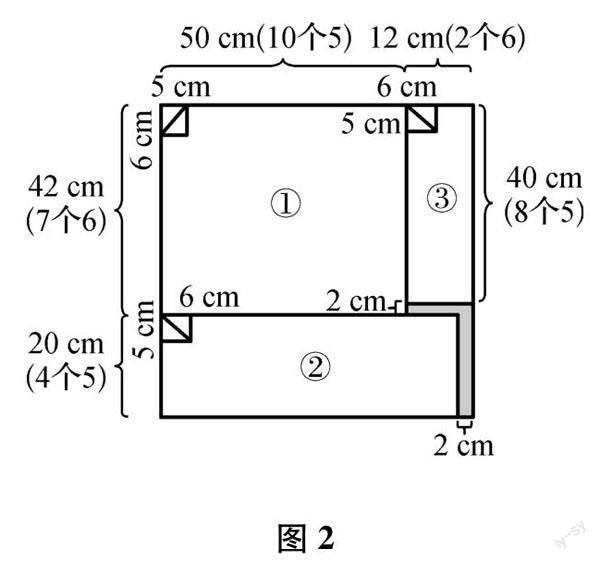
然而，笔者在实际教学中，就遇到几个学生提出这样问题：“按照上面的算法，通过画图后很容易发现，浪费的面积还有不少，虽然不能拼接，難道不能尝试组合使浪费的面积少一点吗？这样剪成直角三角形小旗的面数不就能更多了吗？”在学生可提和敢提问题的背景下，一个课堂自然生成的数学情境，让大家对这个问题进行了重新的认识和思考，通过有效的画图配合解答过程，笔者发现学生的学习真正显示出数学知识“生长的力量”.从一开始初步达成共识的解法来看，可以直观的看出（图1），画阴影的部分是不能再裁剪了，但是这部分的面积确实浪费了不少，问题既然是要剪的最多，学生这里就提出：“可不可以先从少浪费甚至不浪费开始思考？”也便有了新的解答思路（图2），通过图解，很容易把边长为62厘米的正方形分成3大块可以完整裁剪的图形，以及阴影部分不再能利用的图形，很方便就能列出这样的算式：① 62-12＝50（厘米），50÷5=10（个），62-20＝42（厘米），42÷6=7（个），10×7×2＝140（面）；② 20÷5=4（个），62÷6=10（个）……2（厘米），10×4×2＝80（面）；③ 12÷6=2（个），42÷5=8（个）……2（厘米），8×2×2＝32（面）；总计140+80+32=252（面）.

可见，孩子有了想要提出问题的意愿，他们的思维也便打开了，深度学习也就自然进行.经常性有这样的“有问题想提”，学生的创新意识便能不断形成，数学学科的核心素养便能很好地养成.正如许卫兵老师说：教学应该着眼长远，增强学生敢于突破常规、不迷信书本和权威的创新意识，培养勇于探索、善于合作、勤于思考、奋发进取的精神，以及形成正确的世界观、价值观和健全的人格时，课堂就有了丰富的意蕴美^［4］.

4 设计合理情境，让学生有问题乐提

在平时的教学中，教师应遵循学生好奇心好表现自己、爱表扬的实际特点，在课堂教学中要给学生提供多种机会，让他们有针对性的表达想法，乐于提出问题.要想实现学生“有问题乐提”的现象，教师可以设计出一种能够让学生明显意识到的想要提出问题的合理情境.因为合理的情境源于学生现实，其对于学生真实可感^［5］.在合理的情境作用下，让学生产生认识上的困惑时，便是激活他们原有认知的开始，激发他们去进行创新性的探索，自己去乐于发现问题、提出问题，进而有效地解决问题.

例如，笔者在教学六年级上册的《百分数的意义》一课时，在学生正确构建百分数的算术意义后，结合新课标的要求，需要深化体会，认识百分数的统计意义.因此，通过回顾例题情境中每一场的投篮命中率，发现第二场的命中率65〖FGS〗%〖FGN〗是最高的，能看出这一场投的最准.此时可创设这样的情境：如果你是篮球队中的一员，你会有什么问题想问大家？在交流中，就有学生提出：“篮球队如果重新来这四场比赛，还会是其中的第二场投的最准吗？篮球队整体的命中率怎么样？”在交流中不断明确像命中率这样用百分数表示的数据，每一次的结果可能都不一样，是一种随机数据，虽然每次的结果可能都不一样，但会发现这些数据稳定在一定的范围内，具有一定的规律，我们可以根据这些规律进行预测，或者做出决策.借此又创设出本市各区2022年中考四星级高中的录取情况这一情境，学生主动提出2023年各区四星级高中的录取率会怎样？影响各地区录取率的因素可能会有哪些等预判性问题，在问题与问题的交织中，发现仅凭2022年的数据是不够的，要通过随机数据进行预判或决策，需要有大数据进行支撑.学生在进一步的分析和产生的新问题中，不再仅仅停留在数学学习的本身，无形中也提升了核心素养.

综上所述，小学数学“问题提出”的教学，有助于增进教学实效.有效创设出生活情境、真实情境、数学情境、合理情境等多样化情境，学生便会有问题可提，有问题敢提，有问题想提，以及有问题乐提，进而感受数学在现实世界的广泛应用，体会数学的价值［1］.

参考文献：

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［2］ 曹培英.小学数学问题提出的反思性实践研究（上）［J］.小学数学教师，2021（5）：4-14.

［3］ 汪安圣.思维心理学［M］.上海：华东师范大学出版社，1992.

［4］ 徐卫兵.小学数学整体建构教学［M］.上海：上海教育出版社，2021.

［5］ 张丹，吴正宪. 培养小学生问题提出能力的实证研究［J］.中国教育学刊，2017（5）：100-104.