基于演化博弈的区域综合能源市场零售侧竞争策略选择方法
2023-03-23郭吉群朱姝豫勇蔚柯
曹 阳,喻 洁,李 扬,郭吉群,朱姝豫,勇蔚柯
(东南大学电气工程学院,江苏省 南京市 210096)
0 引言
随着电力、热力、天然气等多种形式能源的互联互通与耦合转化,综合能源市场逐渐登上历史舞台[1-3]。在此背景下,参与市场交易的决策主体类型愈发复杂多样,使得零售侧市场中各零售商的收益不仅取决于自身的经济性行为,还与其他零售商的行为密切相关。常用的最优化理论一般以单主体决策为主,其理论体系已无法解决日益复杂的多主体行为决策问题。大多数经典博弈理论,如合作博弈与非合作博弈,均立足于完全理性与完全信息的双重假设,其认为在任何局势下参与者都能对外界的任意变化做出最优的反应[4-6]。显然,市场成员在复杂的决策环境中已无法满足过于苛刻的“双完全”要求。
演化博弈(evolutionary game,EG)是基于有限理性与获取有限信息的条件,运用动态过程研究参与者如何在博弈中调整行为以适应环境与对手,从而产生群体行为趋势的博弈理论[7-9]。有限理性是指参与者无须具备很强的计算能力与推理能力,其决策行为受习惯与偏好等因素的影响,在策略选择时并不总是保持序贯理性。获取有限信息,即信息不对称性,是指参与者无须知晓博弈格局面临的所有可能状态,以及随机抽取状态上的客观概率分布,而是通过已知最有利的策略逐渐模仿下去,最终逐渐达到稳定均衡状态。因此,相比于经典博弈,演化博弈更贴近于综合能源市场中多利益主体复杂经济行为的决策问题[10-12]。
目前,对于采用演化博弈或经典博弈研究市场主体行为决策问题,国内外已有针对各个方向的探讨。文献[13]采用Stackelberg 博弈研究了售电公司在电力市场交易时的竞争策略,并分析了售电市场环境下用户选择售电公司的影响因素;文献[14]从能源经济学的角度出发,建立了传统能源与新能源的演化博弈模型,实现了中小城镇热电联供系统的优化;文献[15]构建了基于演化博弈的电-气互联系统需求响应模型,分析了用户的用能行为趋势及其对系统的影响;文献[16]建立了同质性和异质性发电市场中2 类发电商群体竞价的演化博弈模型,并进行了理论分析与动态仿真;文献[17]对电力现货市场中火电企业报价进行研究,建立了基于遗传算法与演化博弈的阶梯报价策略模型,为不同电力供需场景下的报价提供了参考。
上述文献大都只研究了简单的两方双策略演化博弈,且注重于均衡点稳定性的分析,并未考虑演化参数的变化对稳定均衡的影响机制,也尚未建立起完整的研究体系。同时,对于综合能源市场尤其是零售侧的多群体(三群体及以上)多策略非对称演化博弈长期动态交互行为的研究也较少。本文针对区域综合能源市场中零售侧竞争这一热点问题,以有限理性与获取有限信息的综合能源零售商(integrated energy retailer,IER)为研究对象,建立了零售侧市场演化博弈模型。算例通过分析IER 的演化结果、演化时间及其影响因素,并且与其他博弈方法进行对比,验证了模型的实用性与有效性。
1 区域综合能源市场结构与代理模式
首先,根据中国现有的市场模式构建出区域综合能源市场结构模型,如附录A 图A1 所示。区域综合能源市场主要分为供给侧、零售侧、需求侧3 个部分[18]。市场主体之间主要存在能量流、信息流、资金流3 种关系。供给侧简化为n个发电商、n个热力生产商、n个天然气生产商3 类主体;零售侧简化为n个IER;需求侧简化为n个用户,每个用户均包含电负荷、热负荷、气负荷[19]。
另外,输配运行主体简化为电网、热力管网、天然气管网3 类主体,电力输配又对应于输配分离与输配一体化2 种形式。投资主体简化为n个投资商,其对各类供应商与IER 进行资金投入。电力调度运行部门与其他能源调度运行部门对供给侧与输配运行主体进行管理,综合能源交易中心是各类厂商之间相互交易的平台。
综合能源市场的建立打破了传统能源行业间的壁垒,利用综合能源系统在生产—输配—消费—存储等环节间的耦合性与互补性来实现多能流、多维度的协同优化和不同品位能源的梯级利用,赋予了各市场主体更大的运行可行域与价格弹性,提高了能源供给与需求的灵活性,以获得最合理的能源利用效益[20-21]。根据市场结构的不同,综合能源市场代理模式可以分为4 种[22]:1)综合能源垄断型代理模式;2)综合能源竞争型代理模式;3)分行业垄断型代理模式;4)分行业竞争型代理模式。
由于本文的研究重点为零售侧竞争且需要考虑综合能源之间的协调配合,采用其中的综合能源竞争型代理模式,以分析多个IER 之间的竞争关系。该代理模式的结构如图1 所示,即多个IER 代理该区域用户的综合能源,每个IER 均可代理电力、热力、天然气等多种形式能源,并且它们之间存在竞争关系。

图1 综合能源竞争型代理模式Fig.1 Competitive agency mode of integrated energy
2 IER 竞争策略决策模型
在综合能源零售侧市场中,大用户可自主选择IER 向其出售能量来满足负荷需求,故各IER 之间需要竞争售能。假设总交易周期分为若干个时段,在每个时段结算前,所有IER 将进行一次竞争售能。竞争结束后,各IER 将在该时段按照分配结果出售能量并结算各自收益,然后进行下一时段的竞争售能。
IER 售电的收益函数一般为:
式 中:Pi,t为IERi在t时 段 的 零 售 电 量;为IERi的售电收益系数。
则IERi售电的边际收益为:
IERi售热的收益函数一般为:
IERi售气的收益函数一般为:
式 中:Hi,t和Gi,t分 别 为IERi在t时 段 的 零 售 热 量 和天然气量;和分别为IERi的售热、售气收益系数。同理,通过微分可以得出其售热、售气的边际收益。
IER 在竞争售能时,一般不会直接以其边际收益进行报价,而是根据零售侧市场的博弈情况,在对市场上其他IER 竞争策略进行估计的基础上,适当按照比例动态调整报价[23-24]。因此,设IERi的电力、热力、天 然气的策 略 性报价分别为:
IERi以 预 售 能 量 向 量与报价系数为决策变量,基于自身净收益最大化为 目 标 来 选 择 竞 争 策 略,其 中和分 别 为IERi在t时段的预售热量和预售天然气量。IERi在t时段 售能的净 收益Ii,t为:
3 零售侧市场演化博弈模型
3.1 演化博弈收益矩阵
首先,对交易周期内各方之间的演化博弈做出以下假设:
假设1:博弈参与者数目N=3,三方为3 个不同类型(特性参数不同)的IER(IER Ⅰ、IER Ⅱ、IER Ⅲ)。
假设2:博弈三方均为有限理性的主体,处于完全理性与非完全理性间。
假设3:博弈三方均仅可获取有限信息,做出各自决策时难以确认是利益最大化的选择。
假设4:在区域综合能源市场零售侧中,参与博弈的各IER 均会根据自身特性与外部场景设定2 种竞争策略,策略空间为{高价,低价},低价策略为按约等于边际收益报价,高价策略为按明显高于边际收益报价。每一种竞争策略由其预售能量=和报价系数组成。
假设5:IER Ⅰ、IER Ⅱ、IER Ⅲ选择高价策略和低价策略的概率分别为x、y、z和1—x、1—y、1—z。
假设6:α1、β1、γ1分别为当3 个IER 均选择高价策略情况下各方对应的收益,其他7 种情况同理。
根据以上假设,可得出3 个IER 的演化博弈收益矩阵(2×2×2)如表1 所示。
那些未在产品开发过程中运用模拟仿真技术的人如今都会有些失落:毕竟效率对公司的竞争力起着决定性的作用,即便是中小企业也不能置身事外。一旦有了正确的支持,预想中的困难很快就能迎刃而解。

表1 演化博弈收益矩阵Table 1 Evolutionary game revenue matrix
设IERi在t时段对各类能源的报价均值为:
根据低价优先原则,当IER Ⅰ的报价均值低于IER Ⅱ和IER Ⅲ的报价均值的最小值时,各类能源负荷均优先由IER Ⅰ供给;若还有缺额能量,则由IER Ⅱ和IER Ⅲ供给。当IER Ⅱ的报价均值低于IER Ⅲ的报价均值时,第1 阶段缺额能量减去IER Ⅰ预售能量的缺额能量优先由IER Ⅱ供给,直至满足系统功率平衡约束。其他情况同理。由此,可 得 3 个 IER 在t时 段 的 收 益 参 数αj,t、βj,t、γj,t(j=1,2,…,8)分别为:
其中
3.2 演化博弈局部均衡点分析
本文的主要目的在于采用演化博弈理论找出IER 的最优竞争策略,对应到数学层面,即找出演化博弈的稳定均衡点,而稳定均衡点则在局部均衡点中产生。根据表1 的收益矩阵,IER Ⅰ选择高价策略的期望收益为:
IER Ⅰ选择低价策略的期望收益为:
将其加权后可得IER Ⅰ的平均收益为:
复制者动态(replicator dynamics,RD)用于模拟策略的动态调整过程,以表征博弈主体通过模仿和学习使自身策略调整的反应速度,可用关于选择某一特定策略的概率这一变量的微分方程来描述,即复制者动态微分方程。IER Ⅰ选择高价策略的复制者动态微分方程的值与选择该策略的概率x成正比,并且与期望收益超过平均收益的幅度成正比,即
令R1(x)=R2(y)=R3(z)=0,可解得其在空间N{(x,y,z);0 ≤x,y,z≤1}上 的 局 部 均 衡 点。根据文献[25]的结论,多群体多策略演化博弈的均衡稳定性只在其纯策略处取得,即x、y、z至少有一个等于0 或1。显然,(0,0,0)、(0,0,1)、(0,1,0)、(0,1,1)、(1,0,0)、(1,0,1)、(1,1,0)、(1,1,1)均为其局部均衡点,并且解得的其他局部均衡点均为混合策略。因此,只需讨论这8 个点的渐近稳定性,其余均为非渐近稳定状态。
根据Lyapunov 稳定性理论的间接法可知,分析Jacobi 矩阵在局部均衡点处特征值实部的正负可判定其是否为稳定均衡点[26-27]。若均为负值,则该局部均衡点渐进稳定,即系统在该点处于演化稳定均衡状态;若均为正值,则该局部均衡点不稳定,即系统在该点处于演化不稳定均衡状态;若有正有负,则该局部均衡点为鞍点,即系统在该点处于演化临界状态,仍是不稳定均衡状态。
三维复制者动态微分方程组的Jacobi 矩阵如式(17)所示。
代入具体参数,可得8 个局部均衡点处的Jacobi 矩阵,如附录B 所示。根据Jrd特征值的正负来逐个分析各局部均衡点成为稳定均衡点的条件,如附录B表B1 所示。由表B1 可知,8 个局部均衡点在一定条件下均有可能成为稳定均衡点,且由空间几何关系可知,每个均衡点均与其在正四面体上相邻的3个均衡点互为互斥均衡点,如附录B 图B1 所示。换言之,市场层面的最优竞争策略即稳定均衡点会因实际参数的取值而在此8 个局部均衡点中产生。因此,需要通过具体场景的算例来进一步研究。
4 模型求解方法
求解演化博弈问题的数学本质是求解微分方程组。前文所建立模型中的3 个IER 演化博弈的复制者动态微分方程组为:
式(18)属于三元四次微分方程组,很难通过一般方法求出解析解,并且由于外部场景(各类能源负荷、市场出清价格)是时变的,在不同时段相同策略组合所得到的收益参数(αj,βj,γj,j=1,2,…,8)也不同,从而导致每个时段复制者动态微分方程组的系数(Ak,Bk,Ck,k=1,2,3,4)也在变化,更加无法求出解析解,故只能对其求数值解。本章采用向前Euler 公式,对式(18)进行离散化处理可得:
式中:下标t表示对应变量在t时段的值;h为迭代步长。
根据式(19)可进行迭代求解,即基于向前Euler公式的迭代算法。由此,构成区域综合能源市场零售侧竞争的演化博弈求解流程,如图2 所示。算例采用MATLAB R2020a 进行编程求解。
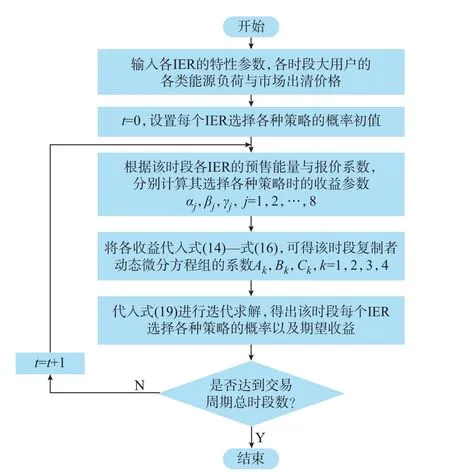
图2 区域综合能源市场零售侧竞争的演化博弈求解流程Fig.2 Flow chart of evolutionary game solution for retail-side competition in regional integrated energy market
5 算例分析
5.1 基础数据
根据实际综合能源市场零售侧竞争的一般情况[23-24],适当设置3 个IER 的收益系数如表2 所示,其2 种竞争策略的预售能量与报价系数如表3 所示。如此设置特性参数使得体量上Ⅰ>Ⅱ>Ⅲ,单位收益上Ⅲ>Ⅱ>Ⅰ,即IER Ⅰ偏向于“大而稳定”,IER Ⅲ偏向于“小而灵活”。

表2 各IER 的收益系数Table 2 Revenue coefficients of each IER

表3 各IER 的竞争策略Table 3 Competition strategies of each IER
设置交易周期为5 d,每次博弈的时间间隔为1 h,即总时段数T=120。每日市场出清电价变化曲线如附录A 图A2 所示,市场出清热价与市场出清气价则视为恒定值,分别为208.33 元/(MW·h)与2.00 元/m3[1]。天 然 气 热 值 为37.26 MJ/m3,迭 代 步长h=0.01。
根据文献[28]的方法,以中国南京市某工业大用户的负荷作为样本数据,采用Homer 软件进行模拟仿真。首先,据此提取出各类能源负荷的时序特征,以此仿真出多个场景下的负荷标幺值;然后,从中选择3 个场景并按照算例系统的规模等比例放大,即得到3 个场景下大用户的电力、热力、天然气负荷的变化曲线,如附录A 图A3 所示。为便于展示,热负荷和气负荷单位已统一为MW。
5.2 IER 的演化结果分析
首先,分析一种初始状态下零售侧竞争的演化结果。本文的初始状态是指在交易周期0 时刻3 个IER 选择某一特定策略的概率(x0,y0,z0)。在场景1下,设置3 个IER 选择高价策略的初始概率分别为x0=0.2,y0=0.4,z0=0.8,其所选策略的演化结果如图3(a)所 示,其 期 望 收 益 的 演 化 结 果 如 图3(b)所示。

图3 各IER 的演化结果Fig.3 Evolutionary results of each IER
由图3(a)可知,在经历约72 个时段后,3 个IER所选择的竞争策略渐进稳定,其稳定均衡点为(1,1,0),即IER Ⅰ与IER Ⅱ的稳定均衡状态为选择其高价策略,而IER Ⅲ的稳定均衡状态为选择其低价策略。
由图3(b)可知,在演化稳定之前,3 个IER 的期望收益均逐渐上升,这与其利润最大化的目标相一致。而在演化稳定之后,三者的期望收益均处于波动状态,且IER Ⅲ的波动更大。其原因在于,由于达到稳定均衡后IER Ⅲ所选低价策略的同 时和分别为520.29 元/(MW·h)和611.00 元/(MW·h)。因此,IER Ⅲ一般能优先向终端用户出售能量,IER Ⅰ随后,IER Ⅱ则在最后出售能量。此时,3 个IER 预售能量之和其 小于大多数情况下的电热气负荷,多余的负荷仍会选择由报价最低的IER Ⅲ来满足,故IER Ⅲ的零售能量会随着各类能源负荷的波动而波动。因此,即使在所选策略不变的情况下,IER Ⅲ的零售能量及期望收益也并不稳定。
分别得出3 个IER 出售各类能源所占据的市场份额,如图4 所示。可以看出,达到稳定均衡后,IER Ⅲ在每种能源的零售市场均占据了50%左右的市场份额,居3 个IER 之首。其原因在于:根据前文分析,达到稳定均衡后IER Ⅲ一般能优先向终端用户出售能量,且其所选低价策略的WbidⅢ,t=[300,200,300]MW,故 其 占 据 了 近 一 半 的 市 场份额。

图4 各IER 的市场份额Fig.4 Market share of each IER
5.3 不同初始状态对零售侧竞争的影响分析
本节分析不同初始状态下零售侧竞争的演化结果。在场景1 下,设置IER Ⅰ的初始概率x0由0 至1以0.2 为步长变化,y0和z0同理,即得到63=216 组演化情况,其所选策略的演化结果如附录A 图A4 所示。在该三维图中,设置第四维时间的值体现在数据点的大小上,所经历的时段数越多,数据点越大。由于该三维图过于复杂,故选取了2 组方位角(Az)和仰角(El)的视点来显示。
由附录A 图A4 可知,若初始状态点位于可行域内部(不位于边界),即x0,y0,z0≠0,1,则均演化至稳定均衡点(1,1,0)。对比3.2 节的理论分析可知,算 例 中 不 同 时 段 的 收 益 参 数αj,βj,γj(j=1,2,…,8)的数值虽然有所差别,但大体上都满足(1,1,0)的稳定均衡条件(α1<α3,β3>β4,γ3>γ7),且几乎均无法满足其他7 个局部均衡点的条件,即与理论结果相符。其原因在于:3 个IER 的收益特性使得预售相同能量时,IER Ⅲ的报价大于IER Ⅰ与IER Ⅱ,且IER Ⅲ本身的体量小于IER Ⅰ与IER Ⅱ,故IER Ⅲ更倾向于预售更多的能量来压低自身的报价,从而更好地与IER Ⅰ、IER Ⅱ竞争。
另外,若初始状态点位于可行域的边界面(不含棱),此时其中一个复制者动态微分方程恒为0,故其演化轨迹仅在该面内;若初始状态点位于可行域的边界棱,此时其中2 个复制者动态微分方程恒为0,故其演化轨迹仅在该线内。
由此可见,在系统参数一定的条件下,博弈参与者最终会演化到何种状态取决于演化的初始位置,即初始状态所在区域决定了最终的稳定均衡状态。若政府或调度运行部门想引导博弈参与者往期望的稳定均衡处发展,则可以通过有效的市场监督或制定合理的奖惩政策,以适当调整系统参数,从而改变稳定均衡条件即(αj,βj,γj),j=1,2,…,8。因此,通过宏观调控使得各IER 在零售侧市场中的最优竞争策略更加趋于合理,以符合实际的市场交易经济性规律,使区域综合能源市场的发展更加健康有序。
另一方面,达到稳定均衡后博弈参与者并未重新出现不稳定状态,这表明演化稳定策略一旦形成,将具备很强的驱逐“入侵者”特性,可抵抗其他变异策略侵入该系统,即非演化稳定策略从此再也不被博弈参与者所选择。
5.4 IER 演化时间分析
对于相同的演化结果,达到市场均衡的时间即演化时间是一项重要特征,故本节分析IER 演化时间的规律。在场景1 下,设置IER Ⅰ的初始概率x0由0.1 至0.9 以0.2 为步长变化,y0和z0同理,即得到53=125 组演化情况,结果如附录A 图A5 所示。
由附录A 图A5 可知,若初始状态下各IER 所选策略均不为纯策略,则其稳定均衡点均为(1,1,0),但其演化时间却有所差别。同时,可定性地看出,IER Ⅲ所需要的演化时间大于IER Ⅰ与IER Ⅱ。其原因在于:根据5.2 节的分析,多余的负荷仍会选择由报价最低的IER Ⅲ来满足,故IER Ⅲ的零售能量会随着各类能源负荷的波动而波动,即IER Ⅲ会被用来平衡各类能源负荷的不确定性,干扰了其演化进程。
对其进行定量分析,将初始状态点(x0,y0,z0)与稳定均衡点(xm,ym,zm)的空间距离即均方根值作为自变量,其演化时间作为因变量。由于演化博弈是一个渐进稳定的过程,本节设当(x,y,z)首次满足|x-xm|<10-2且|y-ym|<10-2且|z-zm|<10-2时 的 时 段数为其演化时间的大小。此处,只研究可行域内部(不位于边界上)的点,其稳定均衡点为(1,1,0)。在场景1 下,设置IER Ⅰ的初始概率x0由0.1 至0.9 以0.1 为步长变化,y0和z0同理,即得到93=729 组演化情况。由此,绘出演化时间关于空间距离的散点图如图5(a)所示。可以看出,整体上空间距离即初始状态下各IER 所选策略与演化稳定策略的差距越大,达到市场均衡的时间越长,且91.5%的情况在40~100 个时段内达到市场均衡。
其次,设首次满足|x-xm|<10-2时的时段数为IER Ⅰ的演化时间,|x0-xm|为x方向距离,IERⅡ与IER Ⅲ同理。由此,绘出单个IER 演化时间关于单方向距离的散点图如图5(b)所示。可以看出,3 个IER 中IER Ⅰ的演化时间最短,大部分在20 个时段内即可达到稳定均衡状态,与附录A 图A5 结论一致。同时,也说明IER Ⅰ的竞争力高于IER Ⅱ与IER Ⅲ,即体量大单位收益小的IER 可在竞争过程中占据主动权,故实际中可向其他类型的IER 适当倾斜一些优惠政策,以保证整个市场不会趋于垄断。由此,可为政府制定市场规则与调控市场交易环境提供一些思路和手段。

图5 各IER 的演化时间Fig.5 Evolutionary time of each IER
5.5 不同外部场景对零售侧竞争的影响分析
对于零售侧竞争的演化博弈,其对外部场景即各类能源负荷变化的适应性是一项重要特征,故本节分析不同外部场景对其演化结果的影响。设置3 个IER 选择高价策略的初始概率分别为x0=0.2,y0=0.4,z0=0.8(与5.2 节相同)。由此,得出在3 种外部场景下各IER 所选策略与期望收益的演化结果如附录A 图A6 所示。
由附录A 图A6 可知,不同外部场景对各IER 参与博弈的演化结果与演化时间的影响均很小,而其对各IER 的期望收益均有一定程度的影响,尤其对IER Ⅲ的影响较大。其原因在于:根据5.2 节的分析,多余的负荷仍会选择由报价最低的IER Ⅲ来满足,故IER Ⅲ的零售能量会随着各类能源负荷的波动而波动,即其在每个时段的零售能量受外部场景变化的影响较大,从而导致其期望收益也受到外部场景较大的影响。
5.6 不同博弈理论的对比分析
与本文算例的研究场景类似,文献[13]采用Stackelberg 博弈研究了售电公司在电力市场交易时的竞争策略。本文所采用的演化博弈与Stackelberg博弈等经典动态非合作博弈相比,其主要区别如表4 所示。由表4 可知,以演化博弈建立的理论体系,更贴近IER 的竞争策略等综合能源市场中多利益主体复杂经济行为的决策问题。

表4 2 种博弈理论的对比分析Table 4 Comparative analysis of two game theories
6 结语
本文以有限理性与获取有限信息的IER 为研究对象,建立了零售侧市场演化博弈模型。算例分析了IER 的演化结果、演化时间及其影响因素,验证了模型的实用性与有效性。结论如下:
1)本文所采用的演化博弈通过假设各IER 都是有限理性与获取有限信息,解决了大多数经典博弈无法解决的综合能源市场中多利益主体复杂经济行为的决策问题。由此,可为零售侧市场中各IER 竞争行为的预测提供一套更先进的方法体系。
2)在系统参数一定的条件下,各IER 最终的稳定均衡状态取决于演化的初始状态。若初始状态下各IER 所选策略均不为纯策略,则体量大、单位收益小的IER 逐渐趋向于选择其高价策略,而体量小、单位收益大的IER 逐渐趋向于选择其低价策略。同时,初始状态下各IER 所选策略与演化稳定策略的差距越大,达到市场均衡的时间越长,而不同外部场景对IER 选择竞争策略的影响很小。由此,可为各IER 如何选择竞争策略以及大用户如何选择IER 提供依据。
3)在各IER 中,体量大、单位收益小的IER 由于其自身特性可在竞争过程中占据主动权,其达到稳定均衡的时间更短、零售收益更稳定且受外部场景变化的影响较小。因此,实际中可向其他类型的IER 适当倾斜一些优惠政策,以保证整个市场不会趋于垄断。由此,可为政府制定市场规则与调控市场交易环境提供一些思路和手段。
未来将结合多种能源转化设备如燃气轮机、电转气、热泵等,考虑IER 利用其进行跨商品套利与多市场交易,进一步研究可套利的IER 的竞争售能行为及其对市场均衡的影响。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
