考虑源荷不确定性的高风险连锁故障快速筛选

朱元振，刘玉田

（电网智能化调度与控制教育部重点实验室（山东大学），山东省 济南市250061）

0 引言

近年来发生的多次大停电事故表明，防范困难的连锁故障是导致大停电的主要原因之一［1-4］。快速筛选出高风险连锁故障，并提出针对性的预防和紧急控制策略，对防止大停电的发生具有重要意义。为研究连锁故障的演化机理，国内外学者提出了OPA（ORNL-PSERC-Alaska）模型［5］、潮流熵模型［6］、相关性模型［7］、基于复杂网络的模型［8］等，但这些模型主要从整体上分析连锁故障对电网的影响，难以用于具体的高风险连锁故障演化路径筛选。

在连锁故障筛选和分析方面，现有研究大多基于事故链搜索的思想，根据前后级故障间相关性的特点，逐级搜索出高风险连锁故障事故链［9-10］。文献［11］考虑线路过载、潮流波动和暂态稳定，提出一种连锁故障事故链预测方法。文献［12］考虑外部天气条件，建立了基于交流潮流的连锁故障搜索模型。文献［13］进一步考虑了多时间尺度下交直流的交互作用，提出交直流连锁故障预测和风险评估方法。文献［14］将网页链接分析方法引入连锁故障研究，可以分析连锁故障传播中的关键环节。文献［15］建立了一种混合学习框架来预测连锁故障和辨识严重初始故障。文献［16］提出一种状态故障网络来识别能够引发高危连锁故障的隐性故障。上述方法均针对确定运行方式，没有考虑新能源大量接入带来的潮流不确定性问题。

针对连锁故障风险评估中的潮流不确定性问题，已有部分学者开展了相关探索。文献［17］针对未来的严重场景分析连锁故障风险，但严重场景的选取具有较强的主观性，对风险评估结果准确性有很大影响。文献［18］采用拉丁超立方采样与Copula 函数相结合的随机潮流计算方法生成多风电场出力场景，针对典型场景生成事故链，但需要进行大量潮流计算，并且其准确性受典型场景选取的影响较大。文献［19］提出了一种考虑风电不确定性及系统调频作用的改进随机潮流方法，由于基于半不变量法建立随机潮流模型，需要假定输入和输出随机变量间呈线性关系且计算过程相当复杂，该方法实际应用难度较大。

在连锁故障风险评估过程中需要进行大量潮流计算，虽然交流潮流算法计算结果准确，但耗时较长。而直流潮流、分布因子（distribution factor，DF）等方法能够大幅提高计算速度［20-21］。由于它们本质上是通过潮流解耦、线性化来提高计算速度，当运行点偏离时，准确度不够。文献［22］利用支持向量机评估多条线路开断场景下分布因子法的计算精度，在误差较大时采用牛顿-拉夫逊法（简称牛拉法）计算，但其未考虑潮流不确定性且特征选取复杂。

本文考虑源荷双侧新能源大量接入带来的潮流不确定性，提出一种高风险连锁故障筛选方法。基于随机响应面法（stochastic response surface method，SRSM）处理风电、负荷等因素带来的线路潮流不确定性，为快速获取连锁故障过程中的线路潮流概率分布，提出一种结合分布因子的改进随机响应面法（stochastic response surface method combining distribution factor，SRSM-DF）。为 降 低潮流线性化带来的计算误差，基于深度森林建立了SRSM-DF 计算误差判断方法，在误差较大时利用基于交流潮流的随机响应面法（stochastic response surface method combining alternative current power flow， SRSM-AC）更新线路随机潮流。为进一步降低不确定条件下连锁故障筛选的计算量，提出了一种两阶段高风险连锁故障筛选策略。将筛选过程分解为高概率连锁故障筛选和连锁故障风险计算2 个过程，可快速求解连锁故障造成的后果及事故链风险。

1 SRSM-DF 基本原理

SRSM 是一种非侵入式概率分析方法，具有计算过程简单且速度较快等优点。其基本原理是用混沌多项式来模拟输入输出的映射关系，通过少量采样确定多项式中的待定系数，进而得到所估计输出响应的概率分布［23］。连锁故障筛选过程中需要反复进行线路开断后的潮流计算。为此，将SRSM 与分布因子法相结合，进一步加快计算速度。

1.1 SRSM 基本原理

对于n维随机变量Χ=［χ1，χ2，…，χn］和输出响应Y，存在函数关系：

若F难以显式表达，则式（1）的计算将较为复杂，采用传统蒙特卡洛抽样求取Y分布的方法非常耗时。此时，可以采用SRSM 建立Y关于输入随机变量X的近似函数关系取代映射关系F，提高计算速度。SRSM 的基本步骤如下。

1）输入变量标准化。将输入的随机变量X变换为标准正态分布变量，变换过程为：

式中：f-1(Φ(ξ))为累积分布函数的反函数；Φ为标准正态分布的累积概率分布函数；ξ为n维标准正态分布变量。

2）建立混沌多项式。对于Y中的某一输出变量y，其与ξ的关系可表示为：

式中：a0，ai1，…，ai1…im为多项式系数；Hm(ξm)为m阶Hermite 多 项 式 ，m=1，2，…，其 中 ，ξm=[ξi1，ξi2，…，ξim]T，ξi1，ξi2，…，ξim为向量ξm中的元素。

多项式中未知系数数量由输入变量的维数n和多项式的阶数m来决定。阶数的增加可提高模拟精度，但同时多项式中未知系数的数量也随之增加，需要大量抽样以确定系数值。研究表明，采用2 阶多项式展开即可达到满意的精度。此外，2 阶多项式中的交叉项对精度提升的贡献较小，通常可以忽略。本文采用了忽略交叉项的2 阶多项式展开式：

式 中：ai为 多 项 式 系 数；ξi为 第i个 标 准 正 态 分 布变量。

3）确定多项式中的未知系数。选择适当的采样点进行计算，确定混沌多项式的未知系数。

4）计算输出响应概率分布。在得到多项式的未知系数后，通过对标准输入变量的大量采样，即可根据式（5）的代数运算快速生成对应的输出随机变量样本，最后可统计得到输出响应的概率分布。

1.2 风电和负荷不确定性描述

在对不确定性描述时，不确定变量可以处理为确定的预测值和不确定的预测误差之和［24］。因此，风电功率和负荷功率的实际值分别表示为：

式中：Pwd和Pld分别为风电功率和负荷功率实际值；和分别为风电功率和负荷功率预测值；ΔPwd和ΔPld分别为风电功率和负荷功率预测误差。

风电功率和负荷功率的预测误差均可以假设服从均值为0 的正态分布。假设风电功率和负荷功率预测误差的标准差分别为σwd和σld，则风电功率服从均值为Pˉwd、标准差为σwd的正态分布，负荷功率服从均值为Pˉld、标准差为σld的正态分布。风电功率和负荷功率的实际值构成了式（1）中的输入变量。

1.3 线路随机潮流

利用牛拉法可计算获得节点电压相角和幅值，线路c的有功功率Pc可写成：

式中：c1和c2分别为线路c的首末节点编号；θc=θc1-θc2，为线路c的相角差，其中，θc1和θc2分别为节点c1和节点c2的相角；Uc1和Uc2分别为节点c1和节点c2的 电 压 幅 值；gc为 线 路c的 电 导；bc为 线 路c的电纳。

本文考虑风电和负荷的不确定性，将风电功率和负荷功率作为输入随机变量，利用SRSM 建立输入变量与支路有功潮流的关系，快速求取支路潮流的概率分布。根据式（5），线路潮流的展开式为：

式中：ac，0，ac，i，…，ac，n+i为多项式系数。

在确定多项式系数时，一般选择0 和m+1 阶Hermite 多项式的根作为样本点。式（9）为2 阶混沌多项式，3 阶Hermite 多项式方程为-3ξi=0，其根为、0 和。通过对式（10）进行求解即可确定多项式系数：[ac，0ac，1…ac，2n]T=

式中：ξ1，0，ξ1，1，…，ξn，2n分别为0，1，…，2n次计算时3阶Hermite 多项式根的值，其基于线性无关原则选择，具体方法可 参考文 献［25］；Pc，0，Pc，1，…，Pc，2n分别为线路c在0，1，…，2n次计算的值，其需要通过2n+1 次交流潮流计算获得。

设第i个输入变量的期望和方差分别为μi和σi，在第j次潮流计算时输入变量为：

式 中：χi，j为 第i个 输 入 变 量 在 第j次 潮 流 计 算 时 的值，即式（1）输入变量矩阵X中的元素，表示风电和负荷的注入功率。利用式（11）可确定风电和负荷的注 入 功 率，通 过 潮 流 计 算 获 得Pc，0，Pc，1，…，Pc，2n的值，再根据式（10）便可求得多项式的系数。

1.4 基于分布因子的随机潮流快速计算

在筛选高风险连锁故障时，众多连锁故障样本需要生成，上述基于2n+1 次交流潮流计算的SRSM-AC 仍然需要大量交流潮流计算。为提高连锁故障筛选过程中的计算效率，提出一种适应于连锁故障分析的改进SRSM。

根据电力系统运行特点，针对式（8）可作如下假设：Uc1=Uc2=1，sinθc=θc，cosθc=1，bc=1/xc，xc为线路c电抗。则式（8）可简化为：

根据式（12），可推导出当多条线路开断后，线路c的 有 功 功 率Pc，Sl为：

式中：Pl为线路l的有功功率；Sl为开断线路集合；Dc，l为线路开断分布因子，其值由节点阻抗矩阵快速计算［26］。

式（13）计算潮流的方法称为分布因子法，在连锁故障筛选过程中，SRSM-DF 采用分布因子法更新多项式系数。Dc，l的计算过程简单且没有迭代，在筛选连锁故障时，采用SRSM-DF 计算潮流概率分布相较于SRSM-AC 计算量显著降低。

SRSM-DF 虽然速度很快，但其缺点是随着开断线路的增加，部分方式下潮流计算结果误差较大，基于该结果的连锁故障分析将不再可靠。为解决该问题，可在计算误差较大时改用SRSM-AC 更新线路随机潮流。随机潮流更新的关键在于准确、快速地判断计算结果的可信度，因此，本文提出了基于深度森林的SRSM-DF 计算误差判断方法。

2 基于深度森林的SRSM-DF 计算误差判断

随机森林是决策树算法的集成，而深度森林则是随机森林在深度和广度上的一种集成［27］。深度森林是近年来提出的一种人工智能方法，具有超参数少、规模根据数据复杂程度自适应改变等特点，能够方便地应用于不同规模电网SRSM-DF 的计算误差评估。

2.1 深度森林

深度森林也被称为多粒度级联森林，图1 所示为深度森林的结构示意图，其包括多粒度扫描和级联森林2 部分。图中，不同颜色的虚线框表示不同大小的滑动采样窗口，不同颜色方框表示对应得到的不同大小的特征向量；RF A1、RF A2、RF B1、RF B2、RF C1、RF C2 为不同结构的随机森林；1A、1B、1C、NA、NB、NC为不同的级联层。

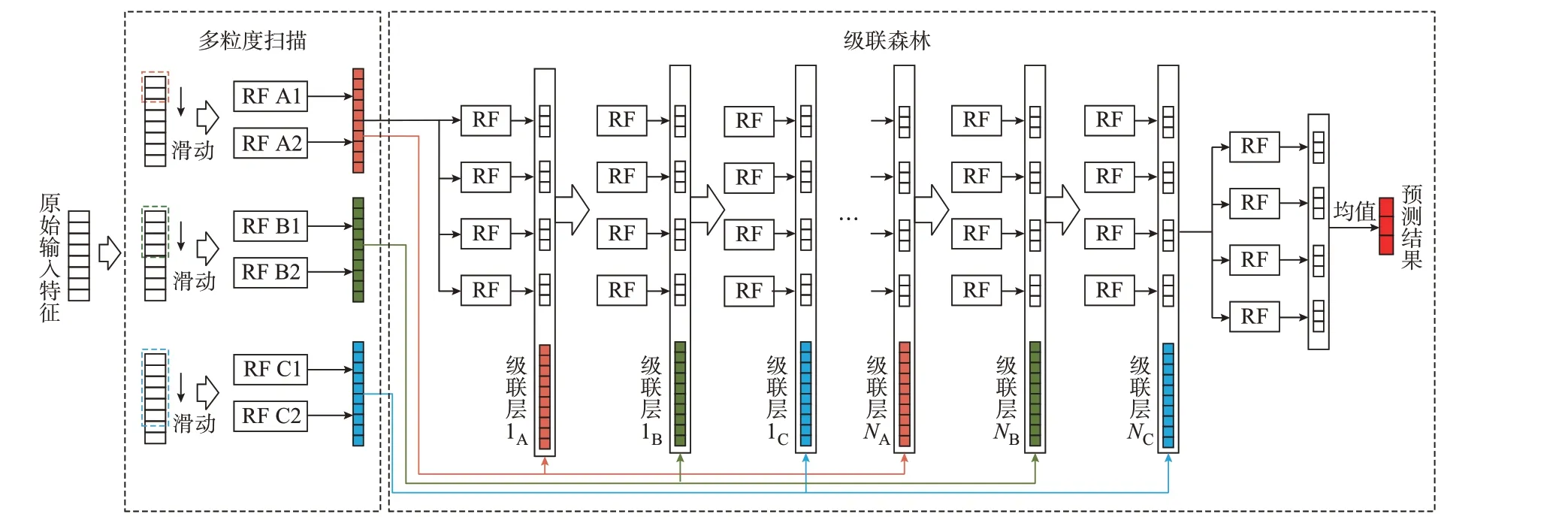
图1 深度森林结构示意图Fig.1 Schematic diagram of structure of deep forest

多粒度扫描通过多个尺度的滑动窗口来获取原始输入中的局部数值，处理得到的结果序列作为随机森林的输入，由随机森林得出每个输入对应类别的概率。将多个森林的多个结果进行拼接作为转换后的特征，用作后续级联森林模块的输入。

级联森林每一层都由多个森林集成得到，其输出和多粒度扫描得到的特征通过拼接作为后一层森林的输入特征。级联森林的每一层可以由多种不同的森林构成，增强对特征差异性的表征。级联森林的层数是自适应的，不用人工提前设定。当扩展一个新的级后，整个级联的性能将在验证集上进行估计，如果无明显的性能增益，则训练过程将终止。

2.2 SRSM-DF 计算误差判断

2.2.1 输入特征选择

SRSM-DF 产生误差的关键在于潮流方程的线性化，即式（8）到式（12）的简化。因此，输入特征的选择应当从简化过程入手，获取能够反映SRSMDF 误差的关键特征。此外，输入特征的计算应当简单方便，避免复杂的计算导致误差判断过程耗费大量时间。

从式（8）到式（12）的简化过程可看出，当线路重载时，线路两端的相角差将变大。此时，sinθc=θc和cosθc=1 的假设将导致误差变大。因此，选择线路两端相角差作为输入特征，线路c两端的相角差可以采用下式估计：

重载时的线路电压降落增加，线路两端的电压幅值差进一步增大，Uc1=Uc2=1 的假设也将给计算结果造成很大误差。因此，选择线路有功功率绝对值|Pc|作为输入特征，可在一定程度上反映电网电压情况。

电气距离能够表征2 个节点之间的电位差，因此，选择关键母线与发电机节点的电气距离作为表征电网电压情况的另一特征。电气距离Zα1-α2表示为［26］：

式 中：zα1α1为 节 点α1的 自 阻 抗；zα2α2为 节 点α2的 自 阻抗；zα1α2为节点α1与节点α2的互阻抗。

在获得各条线路的相角差、有功功率后，对各类特征按从大到小排序，并选择其中排序靠前的部分特征作为输入特征，节点对自阻抗特征无需排序。输入特征向量ε为：

式 中：θ1＞θ2＞…＞θλ；|P1|＞|P2|＞…＞|Pλ|；λ为相角差和有功功率的特征数量；ζ为电气距离特征数量；Zα1-α2，ξ为 第ξ个 电 气 距 离 特 征；ε11，ε12，…，ε3ζ为 特 征向量ε的元素。

2.2.2 误差分类评估

采用线路功率期望的计算误差表征线路随机潮流的计算误差。在Sl中的线路开断后，分布因子法计算的误差指标定义为：

在式（9）中，ac，0即为分布的期望值［23］，即

根据误差指标大小，可将计算结果分为2 类：

在使用深度森林判断SRSM-DF 计算误差前，应建立并训练深度森林模型，其训练过程如下：首先，针对目标电网生成不同的运行方式；然后，在各种运行方式下，随机生成3 级（N-3）故障、4 级（N-4）故障、5 级（N-5）故障，计算输入特征和误差指标并分类，得到训练样本集；最后，利用训练样本集进行训练，获得深度森林模型。

2.3 线路随机潮流更新

连锁故障筛选过程中随机潮流更新流程如图2所示。当多条线路开断后，利用分布因子法计算线路潮流期望值，并获取输入特征向量；利用训练好的深度森林模型评估当前利用分布因子法计算的潮流结果是否准确。若准确，则采用SRSM-DF 更新多项式系数；若不准确，则基于SRSM-AC 更新线路潮流多项式系数。通过该更新流程，可以获得准确度较高的随机潮流计算结果。

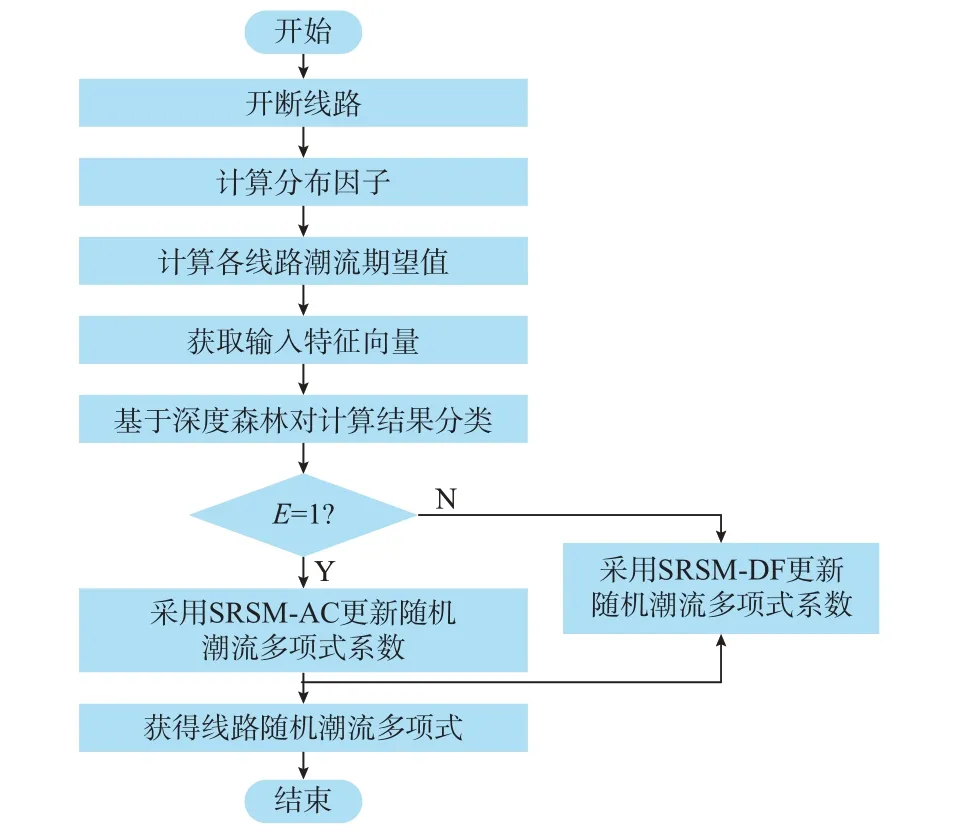
图2 随机潮流更新流程图Fig.2 Flow chart of probabilistic power flow update

3 高风险连锁故障筛选

为评估电网连锁故障风险，提出了高风险连锁故障两阶段筛选方法。阶段1 首先筛选出高概率连锁故障，减小需要风险计算的连锁故障数量；阶段2针对高概率连锁故障计算故障导致的后果，得到连锁故障风险。本文的研究目标是针对交直流混联电网，快速获得预想连锁故障集。因此，为提高计算效率，忽略了故障过程中线路和发电机的暂态稳定问题，重点关注连锁故障对直流的影响。在筛选出高风险故障后，可进一步采用更为准确的仿真方法详细分析故障演化过程。

3.1 高风险连锁故障两阶段筛选策略

高风险连锁故障筛选流程如图3 所示。图中：k为连锁故障级数，K为设定的连锁故障级数上限，Sk为搜索过程中产生的连锁故障集，Mk为Sk中的连锁故障数量，β为连锁故障序号。需要注意的是，开始时k的设置应当根据初始故障确定，比如，当初始故障是N-2 故障时，k=2。

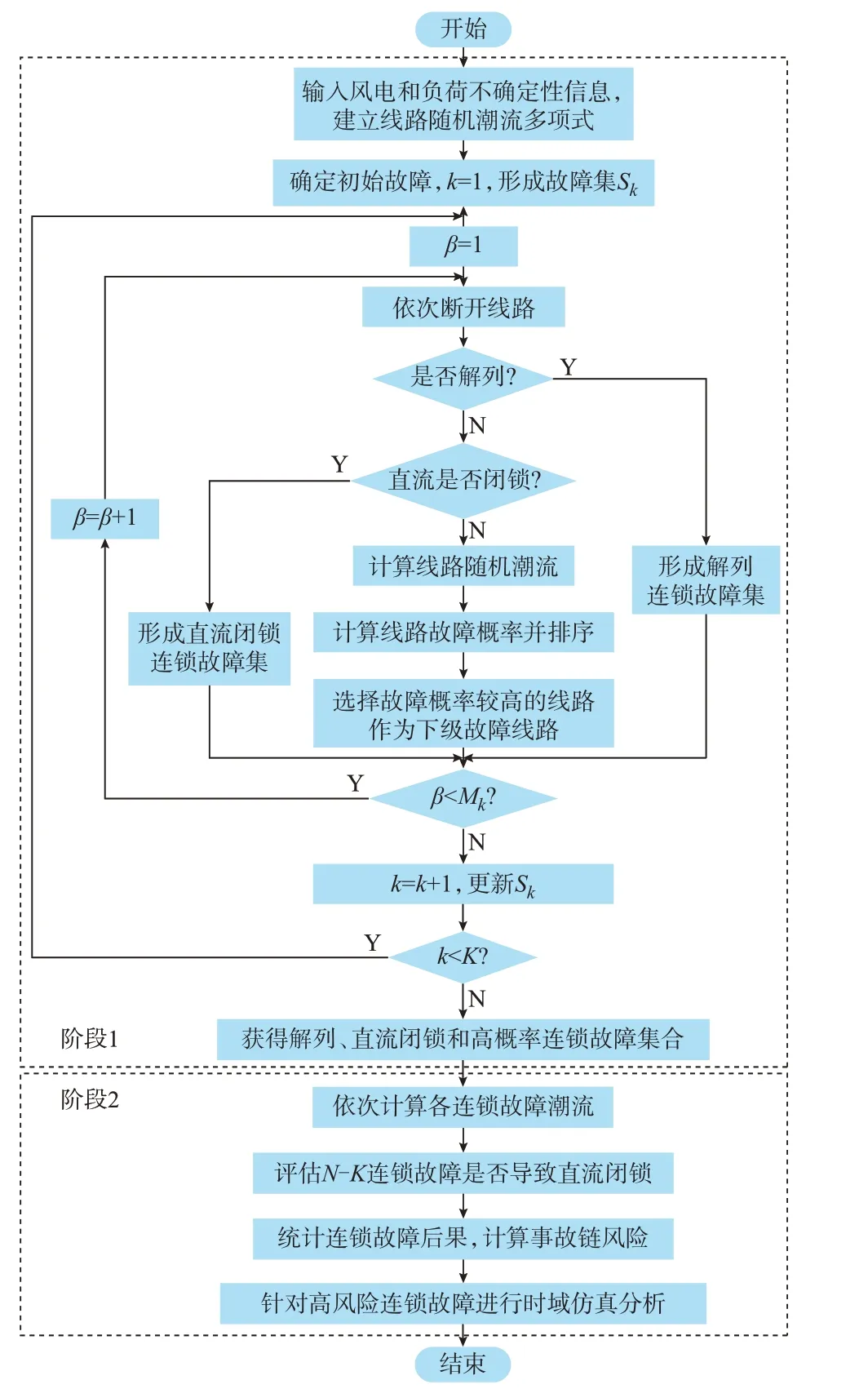
图3 高风险连锁故障筛选流程图Fig.3 Flow chart of screening process of high-risk cascading failures

在阶段1，首先利用SRSM-AC 建立线路潮流多项式并求解多项式系数，在后续的连锁故障搜索过程中，采用图2 所示流程更新随机潮流。在筛选过程中，严重的连锁故障可能导致电网解列或直流系统闭锁。其中，电网解列容易识别，对于导致解列的事故链，应将其纳入解列连锁故障集并终止其后续搜索。而连锁故障对直流系统的影响与故障后交直流电网的动态特性有关，本文提出一种快速评估方法，判断连锁故障是否能够导致直流闭锁，连锁故障对直流系统的影响及该评估方法的具体内容见附录A。

在获得线路随机潮流后，计算各线路的故障概率，选择故障概率较高的线路作为下级故障线路。在故障级数达到上限K后，获得导致解列和直流闭锁连锁故障集以及高概率的N-K连锁故障集，阶段1 结束。

为进一步解释阶段1 的筛选过程，图4 给出了阶段1 筛选过程示意图。图中：l11为初始故障线路，S2和S3即为2 级和3 级连锁故障集。在搜索过程中，首先断开l11，计算随机潮流和故障概率，选择高概率的l22和l23作为下级故障线路，形成故障集合S2。同样，可以得到故障集合S3。依此类推，直到得到连锁故障集SK。

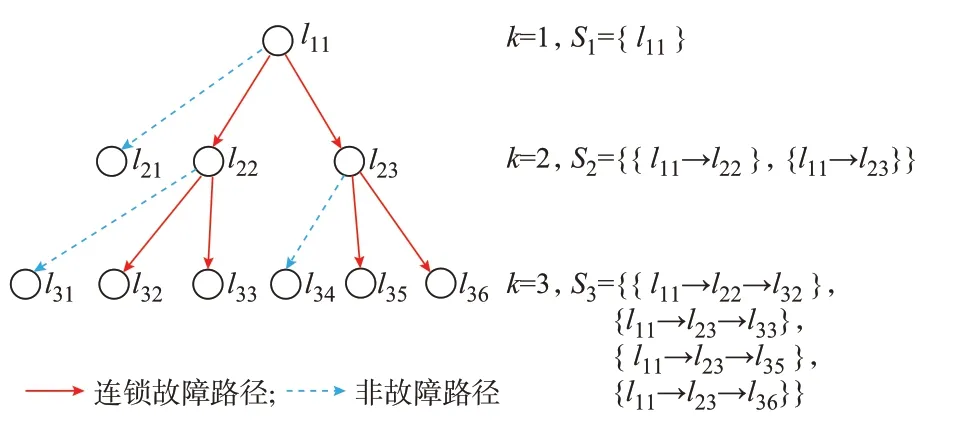
图4 阶段1 筛选过程示意图Fig.4 Schematic diagram of screening process at stage 1

在阶段2 中，针对阶段1 获得的连锁故障集，对集合中的连锁故障按照概率排序并依次计算各事故链风险值。阶段1 评估了前K-1 级故障是否导致直流闭锁；阶段2 在计算风险值时，需要评估N-K连锁故障是否导致直流闭锁，将负荷损失和直流功率损失作为故障后果，综合故障概率和后果，计算得到事故链风险。对于风险较高的故障，可进一步分析故障过程中的动态特性。下面给出连锁故障事故链概率和风险指标的计算过程。

3.2 事故链概率

对于事故链Lk={l1→l2→…→lk}，在获得随机潮流多项式后，可以对输入变量大量抽样后代入式（9），进而获得离散化的线路功率概率密度函数。假设将线路功率分为多个区间，其中，第o个区间为[Po，Po+ΔPo)，ΔPo为第o个功率区间的宽度，则线路功率分布于该区间的概率为：

式 中：Pc，Lk为 事 故 链Lk发 生 后 线 路c的 有 功 功 率；NMC为 抽 样 次 数；N(Po≤Pc，Lk＜Po+ΔPo)为 样 本中线路c功率大于等于Po小于Po+ΔPo的数量。

确定潮流下线路故障率G可表示为负载率的分段函数，二者关系可表示为［17］：

式 中；ηc，Lk为Lk发 生 后 线 路c的 负 载 率，即ηc，Lk=Pc，Lk/，其中，为线路额定功率；为正常负载率下的随机故障概率，其大小应当根据线路所处的外部环境和调度经验灵活调整；ηn为负载率额定值；ηm为负载率极限值。

综合考虑线路功率概率密度和确定潮流下的线路故障概率，不确定条件下线路c的停运概率为：

考虑连锁故障的概率和后果，定义了连锁故障风险指标。事故链LK={l1→l2→…→lK}的连锁故障概率pLK可表示为：

3.3 风险指标计算

交直流受端电网的连锁故障造成的后果主要包括两方面：一是导致电网潮流分布严重不平衡，部分线路严重过载，需要通过切负荷消除线路过载等不正常状态；二是交流连锁故障导致的直流闭锁，造成直流功率的损失。

在阶段1 计算事故链概率时，并没有计算第K级故障后的线路功率。K级连锁故障发生后，线路c的功率为：

式中：ωc为线路c是否故障的状态变量，ωc=0 表示线路c故障，ωc=1 表示线路c未故障；为LK-1故障后线路c和lK开断分布因子。

在不确定条件下，线路功率并不是一个确定值，图5 所示为线路c功率的概率分布，表示累积概率为τ时的线路功率。切负荷和直流功率调整的目的是在一定的置信度τ下，保证线路不过载，即需要调整令其满足。

图5 线路c 功率的概率分布Fig.5 Probabilistic distribution of power on line c

本文将切负荷量和直流功率损失量作为衡量连锁故障严重程度的指标，建立了如下优化模型，其中，式（25）为目标函数，式（26）至式（29）为约束条件。

由于本文考虑了连锁故障导致的直流闭锁事故，ΔPh为从换流母线h处注入受端电网的直流功率。式（26）表示节点功率调整后线路c的功率，式（29）表示功率平衡约束。式（25）至式（29）所构造的优化模型是典型的线性规划模型，可采用成熟的求解器对其求解。综合考虑连锁故障概率和后果，连锁故障事故链LK造成的风险可表示为：

式中：RLK为事故链LK造成的风险。

4 算例分析

针对中国实际华东电网进行仿真分析，该电网包含4 093 个节点、5 345 条交流线路、11 条直流，基准负荷水平为176.944 GW。仿真采用的计算资源为Core i7-6700 3.40 GHz/16 GB RAM。选择2 个大型风电场表征源侧不确定性，采用标准差为1/5期望值的正态分布描述其出力。选择210 个负荷节点表征荷侧不确定性，为简化分析，将负荷节点分成14 类，并假设同一类负荷等比例变化，采用期望为额定值、标准差为1/10 期望值的正态分布描述负荷不确定性。直流功率损失代价因子uh=0.5。

4.1 SRSM-DF 的有效性分析

为验证SRSM-DF 的有效性，以2 000 次基于交流潮流的蒙特卡洛模拟（Monte Carlo simulation，MCS）法作为参考标准，将SRSM-DF 的仿真结果与其进行对比。图6 为在不同故障下采用不同方法仿真得到的绍兴—涌潮Ⅰ线功率累积概率分布曲线。由图中可以看出采用不同仿真方法所得结果接近，说明SRSM-DF 有效。

图6 不同故障下绍兴—涌潮Ⅰ线功率累积概率分布Fig.6 Cumulative probability distribution of power of Shaoxing-Yongchao line Ⅰ with different failures

4.2 SRSM-DF 计算误差判断方法的有效性分析

在判断SRSM-DF 的计算结果误差时，希望判断结果尽可能准确以保证连锁故障筛选的可靠性。

在生成训练样本时，首先生成11 种运行方式，这些运行方式的节点负荷分别为原负荷水平的90%，92%，…，110%。在每种运行方式下，随机选取灵州—绍兴直流落点附近的N-3 故障、N-4 故障和N-5 故障共2 000 个，生成22 000 个训练样本。测试样本则是在负荷水平90%～110%范围内随机生成运行方式，并在灵州—绍兴直流落点附近随机选取N-3 故障、N-4 故障和N-5 故障，共生成20 000 个测试样本。

针对不同的分类标准，利用训练样本训练得到深度森林评估模型，并在测试样本中验证准确率。训练样本和测试样本中的输入特征根据式（16）得到，每个样本包含188 个输入特征。输出为分类类别，误差大于Pˉerr，th时，该样本的类别为1，否则为0。模型包括3 个级联层，训练迭代5 次即达到最优效果。

将本文所提基于深度森林的评估方法与随机森林、二次支持向量机、提升树、线性支持向量机以及决策树等分类方法进行比较，各方法的评估准确率如表1 所示。由对比结果可以看出，在不同分类标准下，本文所提基于深度森林的评估方法均具有最高的准确率，能够有效筛选出计算误差较大的连锁故障，进而可对其采用SRSM-AC 进行计算。

表1 不同方法评估准确率对比Table 1 Comparison of estimation accuracies of different methods

4.3 高风险连锁故障筛选

以绍兴—兰亭双回线和诸暨—舜江双回线为初始故障，分别采用不采取误差判断的SRSM-DF、采取误差判断的SRSM-DF、SRSM-AC 和MCS 法，按照两阶段筛选策略进行高风险连锁故障筛选。筛选过程参考图3 和图4，具体如下。

步骤1：设置故障级数上限K=5，由于初始故障为双回线故障，初始时k=2。

步骤2：依次断开故障集Sk中的线路，判断是否导致系统解列。若解列，则将该故障纳入解列连锁故障集；若不解列，则判断是否导致直流闭锁。若闭锁，则将该故障纳入直流闭锁连锁故障集；若不闭锁，则进行随机潮流计算。根据式（22）得到未故障线路停运概率。

步骤3：选择故障概率最高的10 条线路作为下级故障。

步骤4：重复步骤2 至步骤3，直到Sk中所有故障线路均扫描一遍，得到k+1 级连锁故障集Sk+1，令k=k+1。

步骤5：重复步骤2 至步骤4，直到达到预设的级数上限K。

步骤6：根据式（23）计算各连锁故障概率并排序，得到高概率连锁故障集。

步骤7：针对解列、直流闭锁和高概率连锁故障集合，根据所提风险指标计算方法，计算各故障的风险值。

计 算 随 机 潮 流 时，以Pˉerr，th=5 MW 为 计 算 误 差的判断标准，在连锁故障搜索过程中，10.91%的计算场景下SRSM-DF 计算误差较大。为降低连锁故障风险的计算误差，这些场景需要利用SRSM-AC方法更新线路随机潮流。

图7 所示为以绍兴—兰亭双回线为初始故障，不同方法获得风险最高的前50 个连锁故障的风险值。可以看出，采取误差判断的SRSM-DF、SRSMAC 和MCS 法计算得到的连锁故障风险值结果接近，但不采取误差判断的SRSM-DF 与MCS 法相比，部分计算结果误差较大，影响了高风险连锁故障筛选结果的可靠性。采取误差判断的SRSM-DF、SRSM-AC、MCS 法的计算时间分别为86.7、691.2、8 745.9 s。相较于MCS 法，采取误差判断的SRSMDF、SRSM-AC 等方法在速度方面均有较大提升，采取误差判断的SRSM-DF 与MCS 法相比，计算速度提高了2 个数量级，优势明显。因此，采取误差判断的SRSM-DF 能够兼顾计算速度和精度，是最为合适的随机潮流计算方法。

图7 不同方法连锁故障筛选结果对比Fig.7 Comparison of cascading failure screening results with different methods

此外，用于求取故障后果的线性规划模型单次求解速度小于0.2 s，连锁故障筛选阶段1 初步筛选出了少量高概率连锁故障。因此，阶段2 的连锁故障风险计算时间消耗较少。在筛选高风险连锁故障时，需要进行风险计算的高概率连锁故障数量可以根据实际情况灵活调整，确保满足电网在线安全风险分析的要求。

为进一步分析本文方法在筛选交直流高风险连锁故障方面的有效性，构建了详细仿真策略筛选连锁故障，并与本文方法的筛选结果进行对比。详细仿真策略为利用时域仿真结果评估各级故障发生后电网的暂态稳定情况。同时，为处理不确定性问题，采用MCS 法生成大量运行方式，在每种方式下筛选连锁故障，并将各连锁故障在所有方式下的风险值加和求平均，具体的筛选流程在附录B 中给出。详细仿真策略选择的后续故障线路数量更多，且精细仿真了故障后电网的暂态稳定情况，因此，得到的高风险连锁故障集较为完备和准确。详细仿真策略与本文方法筛选结果的对比如表2 所示。可以看出，详细仿真策略与本文方法的筛选结果非常接近，仅个别连锁故障的排序存在差异。此外，详细仿真策略筛选得到的风险值最高的前50 个连锁故障中，有48 个与本文方法筛选得到的相同。综上所述，本文方法具有较高的准确性。

表2 详细仿真策略与本文方法筛选结果对比Table 2 Comparison of screening results between detailed simulation strategies and proposed method

采用文献［11］的搜索方法筛选连锁故障，并与本文方法和详细仿真策略的筛选结果进行对比。为进一步分析潮流不确定性的影响，基于文献［11］构造了2 种搜索方法。

方法1：构造典型运行方式，其中，风电和负荷功率为期望值。针对该典型运行方式采用文献［11］方法筛选连锁故障并排序。

方法2：利用MCS 法生成100 种运行方式，在每种运行方式下筛选连锁故障，求取各连锁故障在所有运行方式下对应风险值的平均值，按照该风险平均值对连锁故障排序。

为方便与本文方法对比，增加了直流闭锁导致的负荷损失，连锁故障是否导致直流闭锁采用时域仿真法评估。不同方法的筛选结果如表3 所示。

表3 不同方法的筛选结果Table 3 Screening results of different methods

通过仿真发现，方法1 与详细仿真策略相比，存在部分连锁故障的风险排序差异较大的情况，如详细仿真策略中排序为9 至12 的连锁故障，在方法1中的排序为105、107、109、112，差别明显。当考虑潮流不确定性后，即采用方法2 筛选时，筛选结果与详细仿真策略和本文方法较为接近。因此，有必要在筛选连锁故障时考虑潮流不确定性的影响。

在计算速度方面，由于需要考虑不确定性并利用时域仿真判断暂态稳定，详细仿真策略和方法2耗时较长，均需要310 min 以上。本文方法采用了SRSM 计算随机潮流，并且利用人工智能技术进一步加快了计算速度，仿真时间在100 s 以内。因此，计算速度优势明显。

直流换流母线近区的连锁故障会弱化电网结构，降低直流系统抵御扰动的能力。文献［21］分析了交流连锁故障对直流系统的影响，在直流近区多条线路开断后，若再发生一次短路故障则有较高风险引起直流的连续换相失败，甚至闭锁，局部的连锁故障演变成影响全局的交直流连锁故障。新能源的大量接入带来了严重的运行方式不确定性，演化路径预测难度和复杂度显著增加。在文献［21］的基础上，本文进一步研究了交直流受端电网中源荷不确定性对连锁故障演化的影响，弥补了文献［21］只针对确定运行方式分析连锁故障的不足，而且所提方法有效降低了不确定条件下连锁故障分析的复杂度。

5 结语

考虑电网源荷双侧不确定性，本文提出一种高风险连锁故障快速筛选方法。针对筛选过程中潮流概率分布计算量巨大的问题，运用SRSM 和深度森林分别提高计算效率和精度。理论分析和华东电网仿真结果表明，所提出的SRSM-DF 可以快速获取多条线路开断后的潮流概率分布，基于深度森林建立的潮流概率分布误差判断方法能够准确筛选出误差较大的计算场景，采取误差判断的SRSM-DF 在获取潮流概率分布时能够兼顾计算速度和精度。

所建立的连锁故障两阶段筛选策略对事故链概率计算和后果计算进行了解耦，降低了筛选过程的复杂度。综合考虑切负荷和直流功率调整建立了事故链后果指标的线性规划模型，可快速计算事故链后果。

所提方法考虑了潮流不确定性的影响，在计算故障风险时计及了严重连锁故障造成的直流闭锁，能够高效筛选出交直流电网中的高风险连锁故障，是交直流电网安全风险预警与防控［29］的重要基础。

本文在筛选高风险连锁故障时，主要考虑了新能源大规模馈入带来的潮流不确定问题，在今后的研究中将进一步分析电网动态过程对连锁故障传播的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。