含风电场的MMC-MTDC 系统通用频率响应模型

2023-03-23刘昊宇刘崇茹董浩云

电力系统自动化 2023年5期

刘昊宇，刘崇茹，董浩云

（新能源电力系统国家重点实验室（华北电力大学），北京市 102206）

0 引言

为实现“双碳”减排目标［1］，风能、太阳能等清洁能源成为中国能源开发的主流方向［2］。中国“三北”地区和海上的风能资源富集，土地占用矛盾相对缓和，已建成或规划建设多个大型风电基地［3］。基于模块化多电平换流器的多端柔性直流（modular multilevel converter based multi-terminal direct current，MMC-MTDC）输电系统无须电网辅助换相，具备丰富的运行控制方式，契合风电送出需求［4］。因此，大型风电基地经MMC-MTDC 系统并网成为新型电力系统的重要发展方向［5］。

利用含风电场的MMC-MTDC 系统的调频潜能改善电网频率安全意义重大［6］。频率响应特性的研究是开发MMC-MTDC 系统频率调节能力的重要前提［7］。现有频率响应特性分析主要依赖时域仿真［8］。但时域仿真法存在2 个主要问题：1）时域仿真模型无法对系统稳定性进行理论分析，控制系统参数整定依赖于重复试验，不利于工程应用［9］；2）对于风电场经MMC-MTDC 系统并网的复杂系统，时域仿真模型元件众多，建模过程烦琐［10］。

针对上述问题，以含风电场的MMC-MTDC 系统稳定性分析和频率响应特性研究为目标的频率等值模型成为研究热点。在风机频率等值模型方面，文献［11］考虑风机有功功率输出特性，利用二阶线性方程模拟风机功率和转速的关系。文献［12-13］基于最大功率点跟踪（maximum power point tracking，MPPT）方式和虚拟惯性控制，建立了双馈风机的频率等值模型。文献［14］在单机频率等值模型的基础上，根据风电场拓扑结构建立了风电场的频率响应模型。文献［11-14］均面向传统跟网型风机。文献［15-16］针对新兴的构网型风机，根据其主动支撑型控制方式重构了文献［12-13］的频率等值模型。文献［11-16］的频率等值模型未涉及直驱风机。而现有直驱风机小信号模型［17-18］通常仅保留背靠背变流器的网侧，无法反映直驱风机频率响应特性。因此，直驱风机的频率响应模型亟待提出。

在MMC-MTDC 系统频率等值模型方面，现有MMC 小信号模型［19-20］的问题包括：1）一次系统通常使用理想电压源，无法模拟系统频率动态；2）二次系统缺乏对频率控制环节的建模［21］，而频率控制环节是MMC 频率响应的基础［22］；3）侧重于桥臂内部特性的模拟，导致模型过于复杂，对于研究系统有功类分量的动态响应不够直观［23］。

针对MMC 小信号模型研究频率响应的局限，遵照小信号建模思路，MMC 有功类分量等值模型应运而生。文献［24-25］结合MMC 基础控制方式和附加频率控制，建立了单个MMC 的有功功率-频率响应模型。文献［26-27］分别建立了不考虑和考虑附加频率控制环节的MMC-MTDC 系统有功类分量等值模型，前者侧重于分析直流网络电压和有功功率的相互影响，后者更多关注附加频率控制对系统功率、电压动态特性的作用。文献［24-27］均基于连接常规交流电源的MMC-MTDC 系统，未考虑风电场经MMC-MTDC 系统送出的电网新形态。

针对时域仿真模型建模复杂、无法进行稳定性分析和参数优化等问题，本文考虑交流线路传输损耗、风机损耗及换流器损耗，将变流器有功类分量及功率-频率控制解耦出来，建立了完整的含风电场的MMC-MTDC 系统的通用频率响应模型。

1 MMC-MTDC 系统拓扑结构及控制方式

图1 所示为含风电场的MMC-MTDC 系统拓扑结构和控制方式。图中：Pref，G和Ps分别为电网侧变流器（GSC）有功功率参考值及实际值；f和f*分别为频率及其基准值；Udc和Udc，ref分别为直流电压及其参考值；Kf和KV分别为频率下垂系数和直流电压下垂系数；uabc和iabc分别为交流系统三相电压和三相电流；Ud、Uq和id、iq分别为公共连接点（PCC）的d、q轴电压和电流分量；id，ref、iq，ref分别为d、q轴电流参考值分别为风电场侧变流器（WFC）交流侧频率及其参考值；Kowf为频率转换系数；KD和Ki分别为风机等效阻尼和惯性系数；Pref，P和ΔPref，P分别为风机功率参考值及调频功率增量；s为Laplace 算子；PI表示比例-积分控制器。直流电网采用网状拓扑以示通用性，网络中没有纯直流节点。

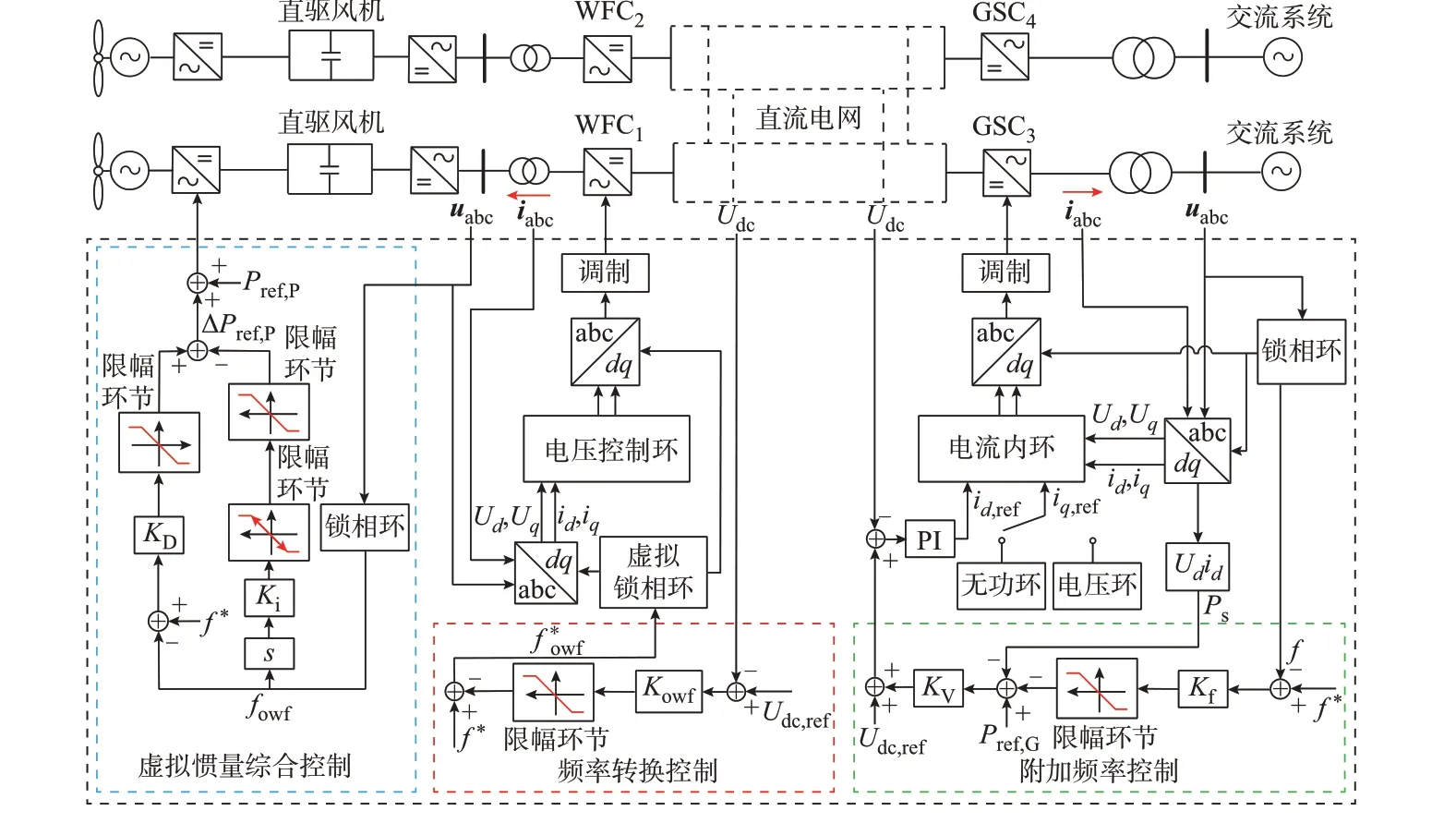
图1 含风电场的MMC-MTDC 系统拓扑结构及控制Fig.1 Topology and control of MMC-MTDC system integrated with wind farms

MMC 采用基于dq轴同步旋转坐标系的矢量控制，其中GSC 的定功率控制和定直流电压控制用下垂控制统一表征［28］。附加频率控制环节［25］解决了GSC 无法响应交流系统频率变动的问题。则GSC有功外环可表示为：

WFC 外环采用定交流电压控制，系统频率由虚拟锁相环直接生成。WFC 频率转换控制［29］将直流电压同WFC 交流侧频率相耦合，即

对于无源系统，在虚拟锁相环的作用下fowf和相等。

直驱风机机侧变流器采用定有功功率控制［30］。正常运行时，有功功率参考值Pref，P为MPPT 模块生成的最大运行功率PMPPT。辅助频率支持时，Pref，P叠加虚拟惯量控制生成的调频功率增量ΔPref，P以增发功率［31］。ΔPref，P定义为：

交流系统发生频率扰动后，式（1）—式（3）的频率控制协同作用完成了网侧至源侧的频率扰动传递，促成了源侧至网侧的辅助频率支持。本文以式（1）—式（3）的频率控制为基础，结合MMC-MTDC系统数学模型，提出系统通用频率响应模型。

2 MMC 及交流系统频率响应模型

2.1 频率响应模型建立基础

MMC 简化模型如附录A 图A1 所示。图中：Us为PCC 电压；Pg为发电机机端功率；Rg、Lg和Rs、Lm分别为线路和MMC 交流等效电阻、电感；idc为直流电流。

基于瞬时功率理论的Ps为［32］：

通常MMC 锁相环定向于PCC 的d轴电压［33］，即Ud=Us、Uq=0。则式（4）化简为：

式（5）的MMC 有功功率计算摆脱了q轴分量干扰。假定PCC 电压恒定，则Ps与id成正比［34］。由于内环控制实现了MMC 的dq轴分量解耦［35］，外环控制的电流参考值能独立生成id。结合式（5）和内外环控制，提出图2 所示的基于d轴分量的MMC 有功闭环控制，为独立分析MMC-MTDC 系统有功类分量动态特性提供理论基础。图2 中：kp1、ki1和kp2、ki2分别为MMC 外环和内环控制器的比例和积分系数；vd为d轴内电势。

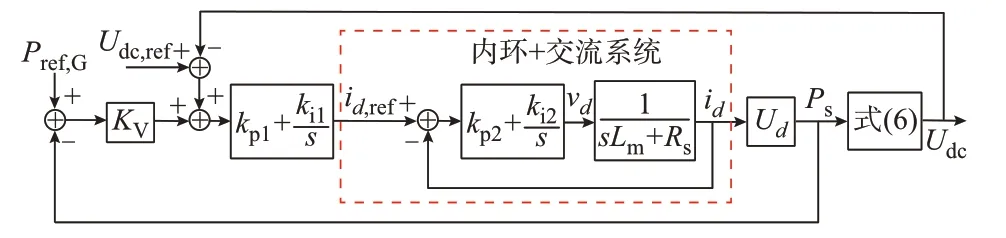
图2 MMC 有功分析模型Fig.2 Active power analysis model of MMC

2.2 GSC 频率响应模型

平均值模型忽略MMC 内部动态，仅关注MMC的能量传递和交直流外部特性［36］，简化了MMC 建模过程，适用于分析MMC 所连交直流系统的频率响应特性。MMC 平均值模型见附录A 图A2。

2.2.1 GSC 直流侧模型

MMC 平均值模型的直流侧数学模型为：

式中：Ceq为MMC 等值电容，计算方法见文献［37］；Iloss为MMC 等效损耗电流；Rloss为等效损耗电阻，通常按稳态有功功率的1%计算［38］；IC和Idc分别为直流侧等效受控电流源的理论和实际电流。

将式（5）代入式（6），线性化为：

式中：Δ 表示偏差量，下标i表示MMC 及所连交流系统编号，下同；idc，ij表示MMCi经直流线路ij流向MMCj的电流；ε1，i、ε2，i的具体表达式见附录A式（A1）。

2.2.2 GSC 交流侧模型

根据式（1）和图2，忽略参考值微分项，可得GSC 交流侧数学模型如下：

2.3 发电机频率响应模型

本文以附录B 图B1 所示经典汽轮发电机为例研究发电机频率响应特性［39］。图中：ωr和ω*r分别表示发电机转速及其参考值；Tm和Te分别表示发电机的机械和电磁转矩；VCV表示汽门开度；KG为调速器调频系数；FHP为高压涡轮（high pressure turbine，HPT）级功率占比；TRH、TCH分别为再热器、主进汽容积和汽室的时间常数；H和D分别为发电机惯性时间常数和阻尼系数。

由附录B 图B1 可知，汽轮发电机的线性化模型为：

式中：xG1表示中间变量。

电磁转矩Te可通过发电机电磁功率Pe间接获取，即

但Pe通常不可测，由文献［40］和附录A 图A1可知：

式中：Ra为发电机电枢电阻；Ig为发电机电流。

Pg可使用Ps表征，即

根据式（11）、式（12），采用附录A 计算可得：

式（13）建立了显性变量Ps和隐性变量Pe的数学关系，以Ps为媒介实现了发电机转速和GSC 有功功率的交互。将式（10）、式（13）线性化后代入式（9），可得：

式中：φ1和φ2的具体表达式见附录B 式（B1）和式（B2）。

式（9）和式（14）构成了完整的汽轮发电机频率状态方程。经典水轮发电机状态方程见附录B式（B3）。

3 WFC 及直驱风机频率响应模型

3.1 WFC 及直驱风机模型简化方法

本文根据容量加权法利用单台风机模拟整个风电场［41］，直驱风机及其背靠背变流器的完整平均值模型如图3（a）所示。背靠背变流器直流线路很短，因此等效直流系统中忽略直流线路阻抗［42］。同时，在网侧变流器定直流电压控制的作用下，背靠背变流器的直流电压维持Udc，ref不变［42］。

图3 直驱风机等值模型Fig.3 Equivalent model of direct-drive wind turbine

根据式（6）和图3，可得PCC1的有功功率Ps1和PCC2的有功功率Ps2的数学关系为：

根据式（15），仅考虑机侧和网侧变流器的功率传递，可忽略图3（a）中的直流系统，得到图3（b）的直驱风机简化平均值模型。

图4 为直驱风机和WFC 简化等值模型。风机采集PCC2的频率fowf用于虚拟惯量控制。而风机功率Ps1经背靠背变流器转为Ps2，再经汇集线路输送至PCC3，利用WFC 传导至直流网络。参照附录A，PCC3的有功功率Ps3为：

式中：Rw、Xw分别为PCC2至PCC3的汇集线路电阻、电抗；Zw=。类似地，仅关注有功功率传递时，也可忽略图4（a）的GSC 和WFC 的交流侧等中间环节，仅保留图4（b）的机侧变流器交流侧和WFC 直流侧模型。

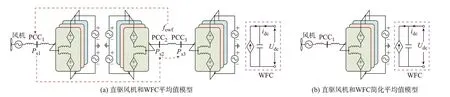
图4 直驱风机和WFC 简化等值模型Fig.4 Simplified equivalent model of direct-drive wind turbine and WFC

3.2 WFC 及直驱风机简化频率响应模型

3.2.1 WFC 直流侧模型

WFC 直流侧数学模型为：

将式（15）、式（16）代入式（17），线性化可得：

式中：γ1，i和γ2，i的计算方法见附录C 式（C1）和式（C2）。

3.2.2 直驱风机机侧变流器模型

机侧变流器正常运行时的有功功率参考值Pref，P为：

式中：kopt为最优功率系数。

将式（19）代入式（8），KV置1，Udc相关项置0，可得风机正常运行时的机侧变流器线性化模型为：

式中：ωr，0为风机当前运行转速。

风机调频时，Pref，P通常由基准功率PMPPT，0和调频功率ΔPref，P两部分构成，即

式中：PMPPT，0为风机启动调频时刻的功率，后续基准功率维持不变以保证风机能够增发功率调频［13］。

将式（17）、式（18）、式（21）代入式（8），可得风机调频时的机侧变流器的线性化方程如式（22）所示，具体推导过程见附录C 式（C3）—式（C10）。

式中：η1，i至η6，i的具体表达式见附录C 式（C9）。

整合式（20）和式（22），风机正常运行和频率支援时的统一状态方程为：

式中：η7，i的具体表达式见附录C 式（C11）。

风机正常运行时令Kowf，i=0，则式（23）化为式（20）。当风机调频时，令kopt，i=0，则式（23）化为式（22）。机侧变流器的vd，i和id，i的状态方程同式（8）一致。

3.2.3 风力发电机模型

相较于汽轮发电机，风力发电机没有调速器，于是风力发电机模型仅需考虑转子运动方程，即

式（24）中Pe可根据式（11）求取。机械功率Pm为：

式中：ρ为空气密度；S为风轮面积；v为风速；Cp为风能捕获系数，其定义详见文献［43］。

将式（13）、式（25）代入式（24）可得风力发电机线性化模型：

式中：φ3和φ4的具体表达式见附录D。

4 含风电场的MMC-MTDC 系统全阶频率响应模型

本文采用模块化设计，将MMC-MTDC 系统中的换流器分为GSC 和WFC 两大类进行内部状态方程构建。以直流线路为接口，实现MMC-MTDC 系统频率响应模型的全局整合。系统状态方程如下：

式中：x为状态变量；u为控制量；A和B分别为x和u的系数矩阵。

1）GSC

根据式（8）、式（9）、式（14），GSCi及其交流系统的状态变量xi和控制量ui分别为：

xi为GSCi内部变量，对应的系数矩阵AG，i、BG，i见附录E 式（E1）和式（E2）。由式（7）可知，GSCi的直流电压除了关乎自身状态变量外，还与直流线路电流相关。定义GSCi对直流线路ij的系数矩阵AG，i-L，ij为：

Udc，i同GSCi的所有直流线路电流均相关。因此，AG，i-L，ij的数量同GSCi的直流线路数量一致。

2）WFC

WFCj及所连直驱风电场的xj和uj分别为：

式中：下标j表示WFC 的编号，下同。

相应系数矩阵AW，j、BW，j见附录E 式（E3）、式（E4）。式（23）中Udc和idc的微分会使WFCj与直流线路相关。参照式（29），结合式（E5），定义WFCj对直流线路ij的系数矩阵AW，j-L，ij为：

式中：Aij，l-j的定义式见附录E 式（E5）。

同样地，AW，j-L，ij的数量同WFCj的直流线路数量一致。 WFCj对直流线路ik的系数矩阵AW，j-L，ik为：

式中：Ldc，i和Rl，ik的定义见附录E 图E1；μi、Lij的具体表达式见附录E 式（E6）。

AW，j-L，ik的数量同与直流线路ij共享端口i的线路数量相同。

3）直流线路

基于T 型线路模型［44］，本文考虑换流器和直流电路平波电抗的影响，从而更准确地表征直流线路动态特性。直流线路ij的数学模型见附录E 式（E6）—式（E8），其状态变量xij为：

直流线路无控制量，系数矩阵Aij见附录E 式（E5）。直流线路ij的系数矩阵与所连MMCi、MMCj及其共享出口的其他直流线路相关。定义直流线路ij对MMCi、MMCj的系数矩阵AL，ij-V，i和AL，ij-V，j为：

直流线路ij对线路ik的系数矩阵AL，ij-L，ik为：

4）MMC-MTDC 系统

根据式（28）、式（30）、式（33），MMC-MTDC 系统的状态变量x和控制量u分别为：

根据式（29）—式（35），MMC-MTDC 系统状态方程的系数矩阵A和B分别为：

式（36）—式（38）仅列出MMC-MTDC 系统的部分换流站和直流线路，其余环节在对应位置补充元素即可。式（27）的状态方程可使用数值计算方法［45］求解。本文的频率响应模型主要针对有功功率突变等小扰动事件，交、直流侧故障时的系统暂态响应特性不属于本文研究范畴。

5 仿真验证

5.1 仿真模型

本文在PSCAD/EMTDC 上建立了图1 所示MMC-MTDC 系统的电磁暂态仿真模型，系统参数见附录F 表F1—表F4。下文数字下标1 至4 分别表示WFC1、WFC2、GSC3、GSC4及其所连系统的序号。

5.2 变风速验证

t=5 s 时，风电场1（简记为WF1）风速由10 m/s变至8.5 m/s。t=20 s 时，风电场2（简记为WF2）风速由10 m/s 变至8.5 m/s。风速变化时转速、频率、有功功率、直流电压仿真对比结果如附录F 图F1—图F3 所示。

由附录F 图F1 可知，WF1风速下降后，在MPPT 的作用下风机1 的转速ωr，1降至0.96 p.u.，引发WF1的有功功率Pw，1由450.03 MW 降至397.64 MW。在下垂控制的作用下，系统直流电压下降，GSC3和GSC4的有功功率开始抬升，其连接的交流系统频率下降。随后WF2也发生风速突变，引起系统直流电压和GSC3、GSC4的有功功率继续变化。最终，风机2 的转速ωr，2稳定至0.96 p.u.，系统直流电压收敛于376.98 kV。依次计算图F1 至图F3 中转速、有功功率、直流电压等状态量在两个风电场风速分别变化后的最大相对误差，结果见表1。

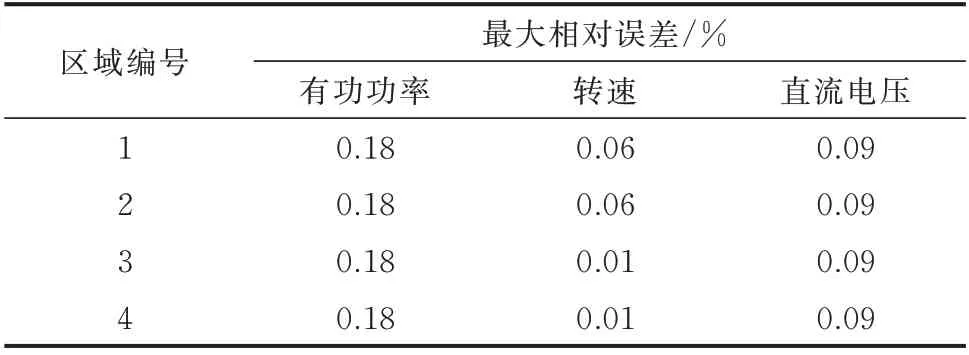
表1 风速变化时不同参数最大相对误差Table 1 The maximum relative error of parameters during wind speed change

由表1 可知，频率响应模型在整个仿真过程中与电磁暂态仿真始终维持一致的变化趋势，MMC-MTDC 系统的有功类分量最大相对误差不超过0.18%，证明频率响应模型具备很高的准确度。

5.3 频率支持验证

t=5 s 时，GSC4机械转矩突降30%，WF1和WF2风速维持10 m/s 不变。频率调节过程中采用的仿真模型及风机控制策略见表2。

表2 频率调节时采用的仿真模型及风机控制策略Table 2 Simulation models and control strategies of wind turbines with frequency regulation

频率调节时转速、频率对比如图5 所示，有功功率、直流电压对比分别见附录F 图F4、图F5。图5中：f3和f4分别为GSC3和GSC4所连交流系统频率。

图5 频率调节时转速、频率对比Fig.5 Comparison of rotational speed and frequency with frequency regulation

由图5 和附录F 图F4、图F5 中的转速、有功功率、直流电压对比可知，GSC4出现功率失衡事件后，无频率调节措施的情况下，受扰交流系统无法利用MMC-MTDC 系统的调频资源。在发电机自身调频能力的作用下GSC4所连交流系统频率f4由50 Hz降至49.16 Hz，跌幅超过系统安全运行边界。应用辅助调频措施后，WF1和WF2通过释放转子动能使有功功率分别由450.04 MW、350.01 MW 提升至465.14 MW、365.04 MW，同时GSC3增发有功功率24.5 MW。在MMC-MTDC 系统的共同作用下，f4仅下跌0.27 Hz，相较于无辅助调频措施减少了67.86%。t=30 s 时，风机启动转速恢复，WF1和WF2的有功功率Pw，1和Pw，2分别降至420.06 MW 和320.04 MW，引发GSC4的频率二次下跌。随后，随着转速逐渐恢复，f4也逐渐提高并稳定。转速恢复期间，f4和GSC4直流电压Udc，4的最小值分别为49.62 Hz 和355.51 kV。

分别统计无辅助调频措施和有辅助调频措施时系统状态量的最大相对误差，结果见表3 和表4。

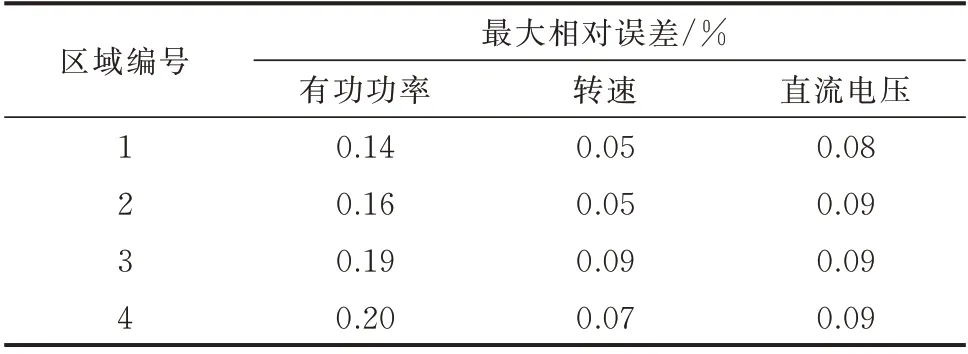
表3 无辅助调频措施下不同参数最大相对误差Table 3 The maximum relative error of different parameters without auxiliary frequency regulation strategy

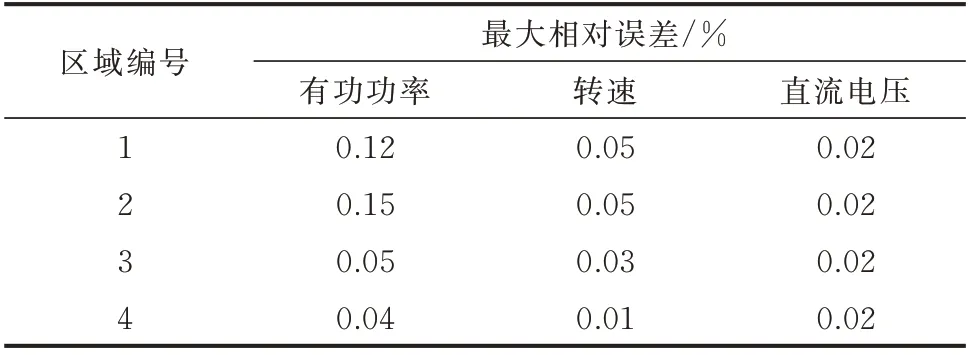
表4 有辅助调频措施下不同参数最大相对误差Table 4 The maximum relative error of different parameters with auxiliary frequency regulation strategy

由表3 和表4 可知，系统功率扰动事件中，无辅助调频措施和有辅助调频措施时，系统有功类状态量的最大相对误差分别为0.20%、0.15%，验证了频率响应模型的正确性。

此外，附录G 中含附加直流电压控制［28］的MMC-MTDC 系统频率响应模型的仿真研究表明，本文频率响应模型对其余有功类控制具有良好的适应性。

5.4 稳定性分析

对WFC、直驱风机和GSC 频率控制的主要参数Kowf、KD、Ki、Kf、KV进行小扰动稳定性分析，特征值分布情况见图6。

图6 系统控制参数小信号稳定性分析的特征值分布Fig.6 Eigenvalue distribution of small-signal stability analysis of system control parameters

由图6（a）可知，频率转换控制系数Kowf，1的5 个主导特征值均位于虚轴左半平面。随着Kowf，1由0升至25，特征值向虚轴右侧运动。由图6（b）、（c）可知，随着风机虚拟惯量综合控制的阻尼和惯量系数KD，1和Ki，1分别由0 升至20 和10，除KD，1的一个位于实轴的特征值向左运动外，其余主导特征值均朝虚轴右侧前进，但始终位于虚轴左侧。图6（d）所示为频率下垂系数Kf，4对系统稳定性的影响。随着Kf，4由0 升至20，4 个主导特征值均向右移动，只有1 个特征值向左收敛于实轴。图6（e）、（f）展示了GSC下垂系数的特征值分布情况。随着KV，3和KV，4的增长，除KV，4的一个特征值向左移动外，其余特征值均向右前移。图6 的稳定性分析结果表明，在正常频率系数范畴内，所有特征值全都分布于虚轴左半平面，MMC-MTDC 系统保持稳定。