基于最小特征轨迹的电力系统稳定器参数整定方法

许 昊，甘德强，黄 润，张 杰，黄 伟

（1.浙江大学电气工程学院，浙江省杭州市 310027；2.云南电力调度控制中心，云南省昆明市 650011）

0 引言

随着特高压交直流输电技术的广泛应用，电网大规模区域互联得到了长足发展。与此同时，由于大规模电能跨区输送，电力系统中以低频振荡和超低频振荡为代表的小干扰稳定性问题日趋严重。低频振荡事故在国内外频频出现［1-2］，而超低频振荡主要存在于水电占优系统中，例如2016 年云南电网与南方电网主网异步联网后出现了超低频振荡［3］。低频及超低频振荡的存在严重制约了区域间电网的大容量功率交换，威胁到电网的安全稳定运行。

为抑制电网中的振荡，提高电力系统小干扰稳定性，通常需要加装控制器，如电力系统稳定器（power system stabilizer，PSS）、调速器等。而如何确定控制器的最优参数涉及小干扰稳定性分析方法的选用。目前针对小干扰稳定性最常用的分析方法是线性化分析方法，包括基于状态空间矩阵特征值的阻尼转矩法［4］、留数法［5］、灵敏度分析法［6-7］等，以及基于传递函数矩阵分析的广义Nyquist 判据［8］、μ分析［9］、相似矩阵法［10］等。

现有的这些小干扰稳定性分析方法大都能为系统的小干扰稳定性分析提供理论支撑，在某些应用场合仍有待完善。例如，阻尼转矩法优势在于物理意义容易理解，但是分析结果较多依赖于数值计算，定性分析较少；状态空间矩阵灵敏度分析法通常用于指导参数调整方向，对稳定裕度的量化分析尚不完善；相似矩阵法多适用于转子回路矩阵对角占优的系统，给出的稳定裕度精度仍待提升。一种工程实用的小干扰稳定性分析方法应当具有严谨的数学基础，并可给出解析且简单的小干扰稳定裕度表达式，从而实现任意控制器的任意参数对于稳定性影响的分析。

针对上述问题，本文从频域角度提出了一种基于最小特征轨迹的小干扰稳定分析方法，并基于此提出了一种控制器参数整定方法。相比状态空间或者多项式模型，电力系统频域模型更加简洁和紧凑，往往只包含几个回路。因此，频域分析可以实现研究对象的简化。该分析方法给出了高精度的稳定裕度，可以量化分析各回路控制器参数对于小干扰稳定性的影响，具有比较严谨的数学基础，适用于电力系统低频振荡及超低频振荡分析。此外，本文基于最小特征轨迹从理论层面解释了PSS 增益存在上界的原因，并给出了励磁模式频率及PSS 临界增益求解方程。

1 小干扰稳定分析的转子回路反馈系统模型

本文所采用的转子回路反馈系统模型是基于Heffron-Phillips 模型变形得到，本质上是Heffron-Phillips 模型的紧凑形式。传统的Heffron-Phillips模型的框图和参数矩阵定义如附录A 所示。

在常规的小干扰稳定分析中，将Heffron-Phillips 模型中的转子环节（sM+KD）-1视作前向通道，其余环节视作反馈环节，得到如图1 所示的转子回路紧凑形式Heffron-Phillips 模型，推导过程详见文献［10］。其中，s为拉普拉斯算子；M为含发电机转子运动惯性常数的对角矩阵；KD为含转子运动阻尼系数的对角矩阵。转子回路将系统分为调速器、转子、有功和无功功率4 个部分，为后续的回路分析带来便捷。

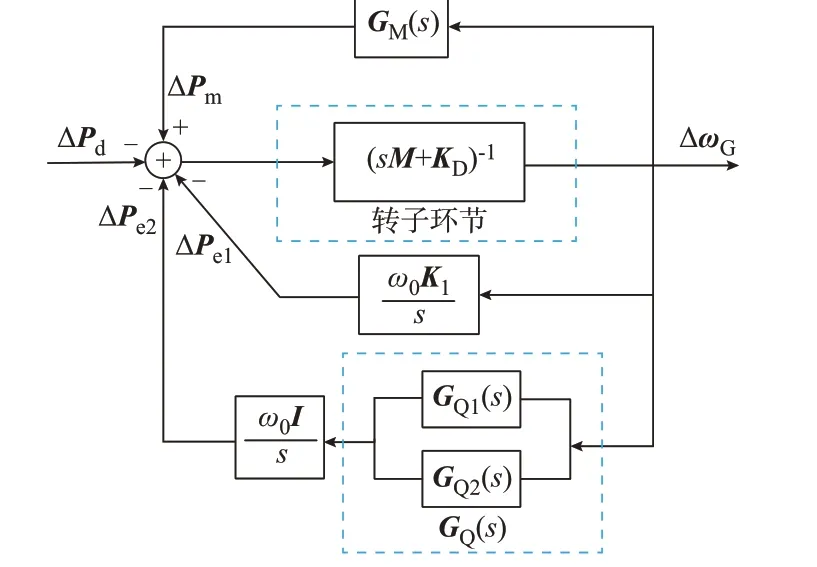
图1 转子回路的紧凑形式Heffron-Phillips 模型Fig.1 Compact form of Heffron-Phillips model of rotor loop

图1 中：ΔPm为原动机输出机械功率列向量；ΔPe1和ΔPe2为发电机电磁功率ΔPe列向量的分量；ΔPd为系统功率扰动列向量；ΔωG为各发电机的角频率列向量；矩阵K1为线性化模型系数矩阵，反映了网络结构、元件参数、运行工况和负荷特征；GM（s）为调速器-原动机系统传递函数对角矩阵；GQ（s）为与励磁系统和PSS 相关的传递函数矩阵，GQ1（s）和GQ2（s）为其子传递函数，其定义分别为式（1）和 式（2）；ω0为 系 统 同 步 角 速 度；I为 单 位矩阵［11］。

式中：GEX(s) 为励磁系统传递函数对角矩阵；ΗPSS(s)为PSS 传递函数对角矩阵；K2，K3，…，K6为线性化模型系数矩阵，反映了网络结构、元件参数、运行工况和负荷特征；为含各发电机d轴暂态时间常数对角矩阵。

传递函数矩阵HPVr(s)定义为：

图1 所示系统对应的回差矩阵［8］为：

式中：L(s)为转子回路开环传递函数矩阵。

在开环传递函数矩阵L中令s=jω，ω为角频率，则有

后文中如不作特殊说明，均默认s=jω。为实现对各个回路进行独立分析，将上述开环传递函数矩阵L进行分解。

因为矩阵M和KD都是对角矩阵，所以

将式（6）代入L并整理得：

定义：

式中：LK1、LKD、LGQ1、LGQ2、LGM分别为和发电机有功功率、发电机阻尼、励磁环节、PSS、调速器相关的开环传递函数矩阵。

可以看到，式（7）将L分解为了和发电机有功相关的LK1、和发电机阻尼相关的LKD、和励磁环节相关的LGQ1、和PSS 相关的LGQ2以及和调速器相关的LGM这几个回路的加和形式，可对各环节分别进行小干扰稳定性分析。下文将以PSS 为例，从回路的角度分析PSS 参数改变对于小干扰稳定性的影响。

2 最小特征轨迹灵敏度法

2.1 频域稳定裕度

根据广义Nyquist 法，可以由转子回路开环传递函数矩阵行列式det（L）环绕-1 点的次数来判断系统的稳定性，进而可将行列式det（L）距离-1 点的距离视作稳定裕度［8］。但是，用行列式来表示稳定裕度存在弊端：高阶行列式计算极其复杂，并且给出的稳定裕度表达式不是解析表达式。特征轨迹稳定判据可视作广义Nyquist 判据的特征轨迹形式［12-13］。该判据无须求解矩阵的行列式，从而达到简化计算、易于分析的目的。

定理1（特征轨迹稳定判据）［13］：若开环传递函数矩阵L有P个不稳定极点，那么闭环系统稳定的充要条件为L的所有特征轨迹逆时针环绕复平面内-1 点 的 次 数 为P次。

其中，L的所有特征值随角频率ω变化的曲线称为特征轨迹。当电力系统采用转子回路模型时，特征轨迹数目与发电机数目m相同。

一般情况下，只需要关心转子回路开环传递函数矩阵距离复平面内-1 点最近的特征轨迹λmin（L），将其称作最小特征轨迹。这是因为当系统中一个振荡角频率为ωo的模式接近临界稳定时，其对应在回差矩阵特征值上的表现是：当ω=ωo时，L（jωo）的一个特征值接近0，该特征值所对应的特征轨迹即将穿越-1 点，而其余特征值均远离-1 点，每条特征轨迹的-1 点环绕次数均为0。当控制器参数发生改变时，不同特征轨迹到（-1，0）点的距离会发生改变，此时，依然将参数改变后距离（-1，0）点最近的曲线称为最小特征轨迹，不影响分析。基于上述原因，可以得到最小特征轨迹稳定裕度［13］。

推论1（最小特征轨迹稳定裕度）：若系统开环传递函数矩阵为L，可将最小特征轨迹λmin（L）到-1点的距离视作该系统稳定裕度Sm。

式中：λi(L(jω))为L（jω）的第i个特征值。

显然，当最小特征轨迹λmin（L）穿越-1 点时，对应于闭环系统矩阵存在一个在虚轴上的特征值，此时，系统临界稳定。

式（9）中给出的稳定裕度是矢量裕度，需要以-1 为圆心作最小特征轨迹的相切圆得到。在稳定分析时选取转子回路反馈系统作为分析对象的另一个优势在于，计算经验表明当系统处于弱稳定时，转子回路的最小特征轨迹接近实轴部分斜率趋近于0。因此，可以通过取最小特征轨迹上实部为-1 的点近似确定系统的振荡频率，该点的虚部为稳定裕度的近似值。

2.2 小干扰稳定量化分析方法

尽管将系统的稳定裕度由行列式简化为单个特征值，但是系统转子回路开环传递函数的最小特征轨迹λmin（L）需要经过复杂的计算才能够获得，并且根据代数学Abel-Galois 理论，高阶矩阵特征值不存在解析解［14-15］，难以解析给出稳定裕度与电网参数的关系，不便开展稳定分析。而文献［10］中所提到的相似矩阵法，尽管解析关系简单，但是适用范围存在局限性。在分析对角占优特性不明显的系统时，特征值的估计精度不够。为此，提出一种基于转子回路特征轨迹灵敏度的小干扰稳定分析方法。该方法可以实现定量分析回路参数变化对稳定裕度的影响。

不失一般性，假设λ1是L（α）的最小特征值，其中α代表了系统中一个变化的参数，v1、u1是其对应的左、右特征向量，有

两边同时对α求导，得到：

将上式写成微分量的形式，有

式中：Δλ1为最小特征值变化量；ΔL（α）为参数微小变化情况下转子回路开环传递函数的变化量。

前文中提到可将转子回路开环传递函数按回路进行如式（7）所示的分解，得到简单相加的关系式，从而实现对各个回路分别进行分析。结合式（7）和式（13）可以实现不同回路参数改变对于不同模式小干扰稳定性影响的定量分析。

上述方法与传统灵敏度法的不同之处在于，传统灵敏度法只能定性且笼统地提供单个参数微小变化时特征值的变化方向等信息，而转子回路经过求偏导后可将各环节对稳定性的贡献写成简单相加的形式，可以求解不同回路、不同控制器对于稳定性的定量影响。由于转子回路的左、右特征向量比较稳定，向量元素值变化很小，可以直接使用式（13）结合原先的稳定裕度，定量给出各个回路控制器参数变化后的稳定裕度变化量，并且具有很高的精度。

以PSS 相位补偿为例。设PSS 的相位为φ，则最小特征值（稳定裕度）关于相位的灵敏度为：

从式（2）与式（7）中可知，L（jω）中仅LGQ2项含PSS 相关项，因此，

当PSS 的增益固定时，ΗPSS是φ的隐函数，尽管求不出∂ΗPSS/∂φ解析的表达式，却可以根据数值计算的方法求其值。

式（14）取偏差量可得：

式中：ΔΗPSS(φ)为相位变化Δφ后PSS 传递函数的变化量。

因此，基于式（17）不难得到PSS 参数变化对于稳定裕度的影响ΔSm即为最小特征值变化量Δλ1。

118 节点系统中，以第1 台发电机所安装的PSS补偿相位为例，确定PSS 的最佳补偿相位。同时，比较当PSS 在振荡频率下取不同相位时，特征轨迹实际稳定裕度、相似矩阵法稳定裕度以及特征轨迹灵敏度法的变化情况。系统参数设置见附录B。

从图2 不难发现，特征轨迹灵敏度法所给出的稳定裕度近似值与实际稳定裕度相差很小，所得PSS 最佳补偿角度均为50°左右；而相似矩阵法给出的近似值误差较大，所得到的最佳补偿角度25°～30°与真实值存在较大偏差。图2 中PSS 相角表示0.68 Hz 下的相角。

图2 不同方法下PSS 最佳补偿相位Fig.2 Optimum compensation phases of PSS with different methods

上述算例说明，当系统转子回路矩阵对角占优特性不明显时，文献［10］中相似矩阵法得到的稳定裕度精度降低，适用范围存在局限性；而特征轨迹灵敏度法则保证了精度，具有较广泛的适用性。此外，还对文献［16］中给出的其余算例进行了相同的测试，得到的结果均佐证了本方法的有效性。

3 基于最小特征轨迹的励磁模式分析

实际工程经验表明，PSS 的增益存在上界，当PSS 输出达到一定值时，会造成励磁系统的失稳，这就是所谓的励磁模式（exciter mode）［17］。通常PSS增益设置为临界增益的1/3 时性能最佳［18］。目前求解临界增益普遍采用的是工程方法：持续增大PSS增益，当励磁调节器的输出电压或者转子电压开始出现持续振荡时，PSS 的增益即为临界增益［18-19］。针对上述情况，基于最小特征轨迹给出了励磁模式频率及PSS 临界增益的数学推导公式，从理论层面解释了PSS 增益不能无限增大的原因。

3.1 临界稳定方程及其简化

根据2.1 节可知，系统中某PSS 的增益发生变化时，对应到复平面上转子回路的开环传递函数矩阵L的最小特征轨迹为一簇曲线；当且仅当PSS 增益达到临界值时，最小特征轨迹恰好首次穿过-1点，最小模特征值为0。因此，临界稳定时，系统的临界稳定方程为：

根据式（18），即可求解励磁模式临界失稳时的临界增益。各类文献对于励磁模式振荡频率范围的阐述稍有出入，大致集中在2～8 Hz 之间［17，20］。在该频段下，转子回路中的相关矩阵存在一些特殊性质，可根据这些性质将临界稳定方程逐步化简。

测试发现，当频率较大时，转子回路开环传递函数矩阵L的对角占优特性十分明显。根据盖尔圆定理（Geršgorin circle theorem）可知，对于任意一个矩阵，其任意特征值都在行盖尔圆之中［21-22］。

当L满足非对角元的值很小时，每行对应的行盖尔圆的半径很小，并且任意一行对角元的值远大于非对角元，基于盖尔圆定理，可以考虑用L的对角元来近似其特征值，这样的近似具有足够高的精度。

不失一般性，假设对全网m台发电机中第i台发电机所安装的PSS 求解其临界增益。结合式（2）至式（4），可知第i台发电机PSS 的增益变化只会影响L的第i列元素，从而只会影响到第i个对角元Lii，使之最先穿越-1 点。因此，临界稳定方程（18）可以近似等价为：

式（19）将临界稳定方程从矩阵方程转化为代数方程，极大地简化了分析。计算经验表明，当频率高于2 Hz 时，GM（jω）值 很 小，且GQ2（jω）≫GQ1（jω）。因此，可以忽略GM（jω）和GQ1（jω），得到：

由于M和KD都是对角矩阵，（jωM+KD）-1也是对角矩阵。文献［6］中提到K1对角元为正，非对角元为负且行和为0，因此，不难看出K1非严格对角占优［23］；而K2对 角 占 优，K3、K6元 素 很 小，GEX（jω）和HPSS（jω）均是对角矩阵，故结合式（2）很容易发现GQ2（jω）在励磁模式频段也是对角占优的。综上所述，L具有很强的对角占优特性。

将式（20）进行展开，式（19）可以改写成：

式中：Mi为对角矩阵M的第i个对角元；KD，i为对角矩阵KD的第i个对角元；K1，ii为K1矩阵的第i个对角元；gQ2，ii为GQ2矩阵的第i个对角元。

Mi、KD，i、K1，ii三 者 皆 为 常 数，可 以 直 接 确 定；gQ2，ii随频率变化而改变。下面着重关注GQ2的对角元gQ2，ii的表达式。在式（2）中，由于T′d0和GEX（jω）都是对角矩阵，且当频率高于2 Hz 时，jωT′d0和GEX（jω）元素的值很大，远大于K3，可将式（2）中K3相关项忽略，得到：

式（22）中，由于(jωT′d0+GEX(jω)K6)-1是对角占优矩阵，且只关注GQ2（jω）矩阵的对角元，在分析时可以忽略非对角元，将其看作一个对角矩阵。考虑 用jωT′d0+GEX(jω)K6对 角 元 的 倒 数 来 近 似(jωT′d0+GEX(jω)K6)-1的对角元。

将GQ2进行展开，可得到：

则gQ2，ii的表达式为：

记hPSS0，i表示增益为1 时第i台发电机PSS 的传递函数。假设当第i台发电机的PSS 增益为K时系统处于临界稳定。则将式（24）代入式（21）整理可得临界失稳方程为：

忽略KD之后，有

式（26）即为最终的励磁模式临界稳定方程。定义式（26）等号左边为励磁模式临界稳定函数Γ（ω，K）；根据ω=2πf也可以将临界稳定函数转变为频率形式Γ（f，K），其中，f为频率。对于一个给定系统，将参数代入（26）后令实部、虚部分别为0 可以得到一个方程组，从而求解系统中各台发电机的励磁模式角频率ωe及PSS 临界增益Kc。

3.2 励磁模式频率与PSS 临界增益

式（26）包含了2 个未知数：励磁模式角频率ωe与PSS 临界增益Kc。将该方程改写为极坐标形式，等号左侧共3 项，注意到第1 项和第3 项都只包含实部，且两项之和为负值，因此要求第2 项为正实数。对第2 项进行极坐标分解，可得：

式中：arg（·）为求相位的函数。

结合式（26）和式（27），可得在励磁模式临界失稳时幅值和增益分别需要满足以下2 个方程：

特别地，PSS 的补偿角度只对式（30）产生影响 。 由 于 |ωT′d0，i|≫|gEX，i K6，ii|， arg(jωT′d0，i+gEX，i K6，ii)≈π/2，当临界稳定时，需要满足：

在对精度要求不高时，可以用式（30）得到励磁模式的近似振荡角频率。式（29）中只包含一个未知数ω，求解之后可以得到励磁模式角频率ωe，将ωe回代入式（28）中求解K可以得到PSS 临界增益Kc。特别地，当ω=ωe时，式（28）等号右侧为常数，等号左侧为关于K的正比例函数，不难看出，PSS 的增益并不能无限增大，从而解释了临界增益的存在性问题。

4 基于最小特征轨迹的PSS 参数整定

4.1 基于最小特征轨迹的PSS 参数设计

安装PSS 之前要求选择合适的参数以保证其具有最优的频率特性，包括相频特性和幅频特性：一方面，要求PSS 在低频振荡频段下提供最佳超前角度，从而补偿励磁系统产生的滞后相位［20］；另一方面，要求PSS 在低频振荡频率下达到尽量大的幅值的同时又不至于因为增益过大引起励磁模式的失稳。传统PSS 由于结构相对简单，在抑制频率较低的振荡模式时的效果并不理想；而新型多频段稳定器PSS4B 尽管可以实现多模态多频段的抑制，由于其高控制自由度增加了控制设计的复杂度［24］。基于此，本文基于最小特征轨迹提出了一种PSS4B 参数的优化设计方法。该方法选取系统各振荡模式的稳定裕度加权值作为性能指标，可以兼顾各个运行方式下各种振荡模式的稳定性，并利用理想相频法的思路确定约束条件，优化设计得到的PSS4B 参数能很好地提高系统小干扰稳定性。

4.1.1 性能指标

对于一个稳定运行的系统，某一时刻系统中某元件参数发生了变化，导致系统在低频振荡模式下的稳定裕度减小，原先的PSS 参数已经不再是最优参数，需要重新整定一组PSS 参数，保证在新系统下PSS 依旧可以为低频振荡提供足够的阻尼，提高系统的小干扰稳定性。

不失一般性，假设λn为L与-1 点距离第n小的特征轨迹，对应第n个模式。设系统共m台发电机安装PSS，令整定参数后的PSS 传递函数对角矩阵为HPSS（s）。根据式（3）和式（16），可得该模式的稳定裕度为：

式中：λsys为系统除PSS 部分的稳定裕度分量，是常数，作为优化目标时可以忽略λsys；vn和un分别为模值第n小的特征值对应的左、右特征向量。

实际系统通常需要同时抑制多个弱阻尼振荡模式。此时，可将系统在这些模式对应频率处的稳定裕度加权和作为性能指标，优化目标为：

式中：N为考虑模式数量；ωn为模式n的振荡角频率；Wn为模式n的权重。

4.1.2 约束条件

1）相位约束

理想相频特性法已在实际应用中证明了其有效性，能够有效抑制本地模式的振荡［17］。参照文献［10］可将式（3）中HPVr的对角元相位随频率变化情况作为理想相频特性曲线整定PSS。为此，可以在低频振荡频段内确定一条理想相频特性曲线，并且所设计的PSS 相频特性不应偏离其太远。假设扫频的角频率为ω1，ω2，…，ωΩ，HPSS的对角元需满足相位约束：

式中：ep为相位误差上界；hPVr，i为HPVr（s）的对角元。

相位约束的引入进一步确保了PSS 在低频段，尤其是本地模式频段提供正阻尼，不会恶化本地模式的稳定性。

2）参数界限约束

对于不同的PSS，设计时还需要根据实际情况、典型参数等给出所设计参数的上下界约束。以采用中心频率形式整定的PSS4B［25］为例，要求PSS4B 的参数满足上下界：

式 中：FL，i、FI，i、FH，i分 别 为 第i台 发 电 机PSS4B 低、中、高 各 支 路 的 中 心 频 率；KL，i、KI，i、KH，i分 别 为 第i台发电机PSS4B 低、中、高各支路的增益；TL，i、TI，i、TH，i分别为第i台发电机PSS4B 低、中、高各支路各环 节 的 时 间 常 数；FL，imax、FL，imin、FI，imax、FI，imin、FH，imax、FH，imin、KL，imax、KL，imin、KI，imax、KI，imin、KH，imax、KH，imin、TL，imax、TL，imin、TI，imax、TI，imin、TH，imax、TH，imin分 别 为 相 应变量的上、下界，根据实际工程要求给出。PSS4B的详细结构及中心频率形式整定思路见附录C。

3）确定临界增益

式（32）至式（35）构成了PSS 参数设计的优化模型，求解该模型可以得到一组提供合适补偿相位且具有最优幅频特性的PSS，可以实现对系统中弱阻尼振荡模式的抑制。若进一步增大PSS 增益，则系统低频振荡模式阻尼可得到进一步增强。但为避免励磁模式失稳，PSS 的增益不能无限增大，存在临界增益。根据式（28）可以求解PSS 的临界增益Kc以及励磁模式的振荡频率fe。在得到各台发电机PSS 临界增益后，将最终的PSS 增益取为临界增益的1/3［18］。

4.1.3 设计流程

所提出的基于最小特征轨迹的PSS 参数优化方法的具体设计流程如下。

步骤1：在每个弱阻尼模式频率下计算式（31）得到相应稳定裕度，并设置各弱阻尼模式的权重，得到式（32）作为优化目标。

步骤2：计算式（3），将HPVr的对角元作为理想相频特性曲线相位，根据式（3）得到相位约束式（34）。

步骤3：设置PSS4B 各参数的上下界，得到参数界限约束式（35）。

步骤4：用计算机软件求解式（32）至式（34）构成的优化模型。

步骤5：求解式（27），解得各发电机的临界增益。将PSS 增益设为临界增益的1/3，得到最终设计的PSS4B 参数。

4.2 仿真算例

通过四机两区域系统以及云南电网仿真算例验证所提方法的有效性。算例时域仿真与模式分析均在DIgSILENT PowerFactory 环 境 中 进 行，PSS 优化模型的求解使用了MATLAB Optimization Toolbox。

4.2.1 四机两区域系统算例

四机两区域系统的结构图在附录D 中给出。原先系统中存在频率为0.54 Hz 及1.08 Hz 的2 个振荡模式。利用4.1.3 节中的设计流程整定发电机G1、G2 上安装的PSS4B 参数，优化设计模型及所得参数详见附录D。

1 s 时在线路a 上发生三相短路故障，0.1 s 后故障清除，线路a 上有功功率波形变化如图3 所示。可以发现，所设计的PSS4B 增强了振荡阻尼，提高了系统的小干扰稳定性。

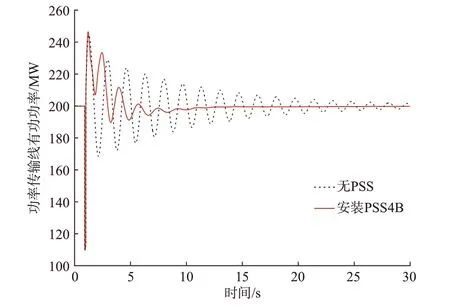
图3 四机两区域系统安装PSS4B 前后系统功率振荡波形Fig.3 Oscillation curves of system power before and after installing PSS4B in four-unit two-area system

安装PSS4B 前后系统振荡模式特征值如表1所示。由表1 可以发现，设计得到的PSS4B 同时提高了2 个振荡模式的阻尼，验证了本文方法的有效性。

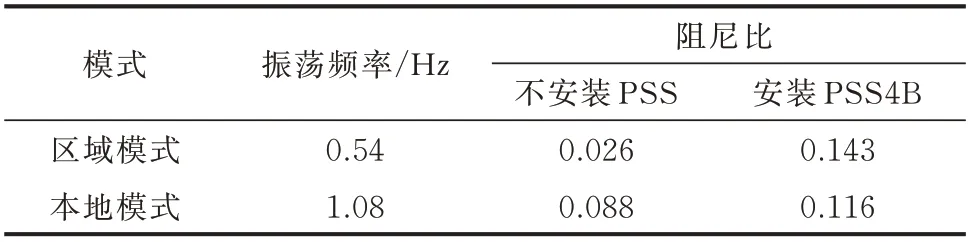
表1 四机两区域系统安装PSS4B 前后系统阻尼比Table 1 Damping ratios of system before and after installing PSS4B in four-unit two-area system

4.2.2 云南电网算例

云南电网冬大运行方式下存在0.622、0.678、0.838 Hz 的3 个弱阻尼模式，夏大极限运行方式下存在0.571 Hz 和0.858 Hz 的2 个弱阻尼模式。通过所提出的方法设计PSS4B 参数以同时提高2 种运行方式下的各振荡模式阻尼比。

根据各振荡模式下发电机的参与度选定LY1G、AH4G、LDL1G、SJH1G、XLD10G 这5 台发电机安装PSS4B，利用4.1.3 节中的设计流程整定5 台发电机上安装的PSS4B 参数，优化设计模型及所得参数详见附录E。

0.5 s 时发生三相短路故障，0.1 s 后故障清除。2 种运行方式下功率传输线上有功功率波形如图4所示。图中：PSS2B 为双通道PSS。由图4 可以发现，所设计的PSS4B 增强了各振荡模式的阻尼，提高了系统的小干扰稳定性。

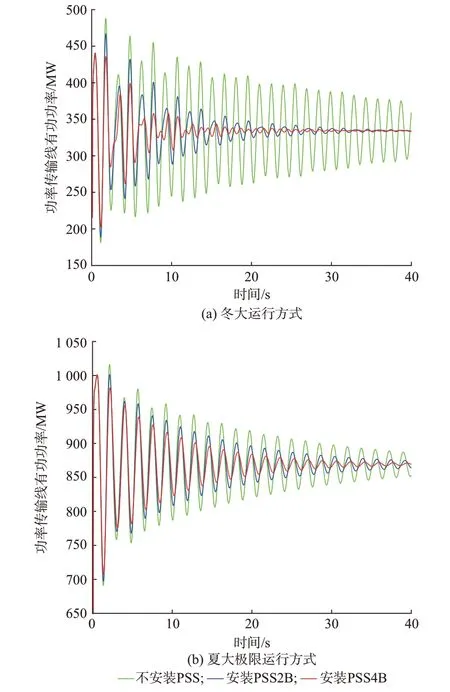
图4 云南电网安装PSS4B 前后系统功率振荡波形图Fig.4 Oscillation curves of system power before and after installing PSS4B in Yunnan power grid of China

安装PSS4B 前后系统振荡模式特征值变化见表2。由表2 可以发现，设计得到的PSS4B 能同时提高2 种运行方式下各振荡模式的阻尼比，且效果优于原先所安装的PSS2B，说明基于本方法设计所得的PSS4B 参数效果良好，从而验证了本文方法的适用性。

表2 云南电网安装PSS4B 前后系统阻尼比Table 2 Damping ratios of system before and after installing PSS4B in Yunnan power grid of China

5 结语

本文从频域角度出发，基于最小特征轨迹提出了一种稳定分析的新思路。相比状态空间或者多项式模型，电力系统频域模型更加简洁且紧凑，可实现研究对象的简化。

1）提出了基于最小特征轨迹的小干扰稳定性分析法，将开环传递函数矩阵最小特征轨迹到-1 点的距离作为稳定裕度，可以将稳定裕度表达为不同回路的加和形式，实现了对控制器回路的单独分析。

2）针对最小特征轨迹所得灵敏度，利用灵敏度法实现了控制器参数改变对稳定性影响的定量分析。

3）利用最小特征轨迹从理论层面对励磁模式进行了数学推导，给出了励磁模式频率以及PSS 临界增益的解析求解方程。

4）以PSS4B 参数为例，给出了基于最小特征轨迹整定方法的一个应用实例，并通过算例证明了该方法的有效性与实用性。

所提出方法基于Heffron-Phillips 模型提出，目前只适用于采用3 阶发电机模型的系统，后续工作将对更普适的高阶模型分析方法展开研究。此外，测试中初步发现该方法可以在新能源电力系统中推广应用，下一步将对所提方法在新能源系统中应用的可行性进行验证。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。