GA−COA求解柔性作业车间多资源调度问题

姜鹏，方成刚，杨帆

（南京工业大学机械与动力工程学院，江苏 南京 210000）

1 引言

制造业是国民经济的支柱性产业“，工业4.0”以及“中国制造2025”的背景下，制定合理的车间调度方案是企业掌握核心竞争力的基础。柔性作业车间（FJSP）突破了传统作业车间加工机床唯一性的约束，越来越适用于当今小批量、多品种的生产模式，且在实际作业车间中需考虑多种资源的分配，因此研究柔性作业车间多资源调度（MRFJSP）具有重大的理论意义和实际价值。

近年来，国内外学者一直注重对MRFJSP的研究。文献[1]将自动导引小车（AGV）与机器调度同时考虑，利用改进的遗传算法求解。文献[2]考虑工件制造、装配以及运输，提出了一种考虑装配及组装的MRFJSP，并通过带优选策略的粒子群算法进行求解。文献[3]提出基于时间窗和Dijkstra算法的混合遗传算法，求解综合考虑机器调度和多AGV 路径规划的调运输和处理时间有限的FJSP。文献[4]利用带禁忌搜索的遗传算法来解决一个考虑运输和处理时间有限的FJSP。文献[5]建立考虑运输和多个机器人的MRFJSP 模型，在粒子群算法中混合了局部搜索算法求解该问题。文献[6]提出一种包含运输约束的调度析取图模型。文献[7]建立包含运输时间的FJSP混合整数线性规划模型，运用混合模拟退火算法的自适应帝国竞争算法求解该问题。文献[8]提出一种遗传、粒子群混合算法，用于求解包含运输、装配的MRFJSP。

郊狼优化算法（COA）是2018年文献[9]提出的，其是通过模拟郊狼成长、生与死、被驱离等现象的新型全局优化的群体智能算法。文献[10]首先将此算法运用在复杂函数和医学图像等方面，并通过实验证明，其具有良好的全局搜索能力和收敛速度。

从以上文献发现：大多数考虑运输的FJSP调度模型均假设所有工件的原材料在0时刻都可开始加工，且未考虑工件成品回库，仓储作为工件原材料、成品的存储设备，是车间调度中不可忽视的一环节，与运输处于同等重要的位置。因此，在目前的考虑运输的FJSP调度模型的基础上，进一步细化、完善调度模型，加入仓储资源约束，建立考虑仓储及运输的MRFJSP调度模型。针对该问题设计了一种遗传—郊狼混合算法（GA—COA），运用算例进行验证，将GA−COA 与遗传算法（GA）和郊狼优化算法（COA）对比，并对模型和算法进{1，2，···，n}，p={1，2，···，Cn}。

2 问题建模

本问题的加工完成时间为工件最终回库时间，以最小化完工时间为目标函数，即行分析。

该车间调度问题的数学模型存在以下约束：

3 问题描述

柔性作业车间中有n个工件，m台机床，一台AGV，每个工件有多道工序，每道工序可选一台或多台机床进行加工，工序在不同机床上的加工时间不同。AGV用于工件在仓库与机床、机床与机床之间的运输，AGV每次仅运输一个工件，且工件的第一道工序由AGV从立体仓库中取出该工件的原材料运至对应机床的线边库后开始加工、工件的最后一道工序完成后由AGV将其运回仓库。

每台机床间的距离相等，因此AGV在每台机床间的运输时间相同，且AGV空载、负载的速度不变；线边库有充足的存储能力，并将上下料等准备时间考虑到机加工时间内；最后一个工件回库标志着整个加工的结束。变量符号定义，如表1所示。

表1 符号定义Tab.1 Symbol Definition

Xipj为布尔变量，若工件i的工序p由机床j加工，则Xipj=1，否则Xipj=0，其中，i={1，2，···，n}，p={1，2，· ··，Cn}，j={1，2，···，m}；Yipjt为布尔变量，若t时刻机床j加工工件i的工序p，则Yipj=1，否则Yipj=0，其中，i={1，2，···，n}，p={1，2，···，Cn}，j={1，2，···，m}；Zipt1t2为布尔变量，若AGV在t1到t2时刻运输工件i的第p道工序，则Zipt1t2=1，否则Zipt1t2=0。

（1）工件的一道工序只能同时由一台机床加工，不能由多个机床加工。

（2）一台机床只能同时对一个工件的一道工序进行加工。

（3）AGV小车一次只能运输一个工件。

（4）任一工件的第一道工序均是从仓库中取出工件原材料运输至该工序所对应的机床线边库中。

这里定义初始工序：该工序是此工艺路线中第一道工序；设仓库位置简称为M0，机床m所在位置简称为Mm。

若工件i的第一道工序是初始工序，对应的机床为j，则工件i的第一道工序开始加工时间为：

若工件i的第一道工序不是初始工序，则工件i的第一道工序开始加工时间为：（TAGVx0中x代表：该工序的前一道工序所在的机床为Mx，则该机床所在位置也是x；设该工序所在的机床为My，该机床y可开始加工时间为：TMSy）

（5）工件的前后工序不在同一台机床上加工，则下一道工序的开始加工时间根据前道工序的完工时间、AGV当前可开始使用时间、AGV在机床间的运输时间以及负责下一道工序的机床的可开始加工时间而定。

假设工件i的第p和p+1道工序分别在机床j1和j2上加工，运输工具AGV小车当前所处机床为r。若TAGVS+TAGVrj1−TFipj1≤0，则：

4 算法设计

GA 的交叉步骤只是针对父代种群中的部分染色体进行操作，不具有全局性。COA有多组结构这种良好的搜索框架，有较强的搜索能力，且COA组内郊狼的成长、生与死，有一定的全局搜索能力，但多组结构使得组与组之间的信息不联通，导致后期收敛速度慢。因此，针对以上GA和COA的特点，提出一种带随机动态分组的GA—COA混合算法，可以很好地解决MRFJSP问题。采用一个实例来描述GA—COA混合算法具体步骤，工件加工及运输信息，如表2所示。

表2 工件加工及运输信息表Tab.2 Workpiece Processing and Transportation Information Sheet

4.1 编码，种群初始化

此处采用基于工序的单层编码，将工件回库作为该工件的最后一道工序，设机加工时间为0，仅需AGV运输时间，最后一个工件的回库代表着整个加工流程的完工。编码为：111122223333，初始化随机将其打乱，可得：123321213123，i出现的次数j表示工件i的第j道工序，最后一个i表示其回库。

4.2 解码，适应度函数计算

以上述编码123321213123为例，解码步骤如下：

（1）在每道工序的可选机床中随机选取机床，可得相应的机床号：[M1 M2 M3 M2 M2 M3 M1 M2 M1 M0 M0 M0]

（2）以编码顺序可得到AGV相应的运输顺序，根据运输顺序和相应的机床号可得到AGV的运输路线。

运输顺序为：O1，1→O2，1→O3，1→O3，2→O2，2→O1，2→O2，3→O1，3→O3，3→O1，4→O2，4→O3，4，其中工序O1，4、O2，4、O3，4表示该工件加工完成由AGV运回仓库中。

以完工时间最短为目标函数，求解值的大小对应该组染色体的优劣。

4.3 精英选择，随机动态分组

组内染色体的成长受组内alpha 染色体和组文化趋势的影响，若alpha是局部最优染色体，则可能导致收敛慢、易陷入局部最优。因此，利用精英选择策略，将其作为全局引导的组内newalpha染色体，并放入子代种群，使算法加快收敛速度，更好地向全局最优解逼近。

COA的多组结构对性能影响较大，N（种群规模）=Np（组数）×Nc（组内个体数）。在N固定不变的情况下，Np越大，Nc越小，全局最优解的作用强；反之，全局最优解的作用弱。采用动态分组方式，根据文献［12］，每组的个体数Nc限制在14以内，有利于各组之间的信息交流，增加郊狼的多样性。假设N=100，Np和Nc必须是100的因子且Nc必须大于3，所以Nc可为4、5、10。在算法迭代前期，设Np=10、Nc=10，全局搜索能力强；在算法迭代后期，设Np=20、Nc=5，局部搜索能力强。随机动态分组的采用，可省去COA的郊狼被驱离这一步骤，改善算法的操作性能。随机动态分组，计算第p组第c个染色体的社会适应能力SOCp，c。

其中，lbc和ubc—染色体社会因子的下界和上界，rand为［0，1］内均匀分布的随机数。

4.4 组内染色体成长、生与死

确定全局最优染色体newalpha、组内文化趋势culture（也称组内中值染色体），随机选取组内两条染色体Cr1、Cr2。组内染色体成长受δ1和δ2的影响，δ1为alpha与Cr1的差异、δ2为culture与Cr2的差异。

组内染色体成长的新解：

更新组内染色体成长后的社会适应度值，

组内染色体成长后，通过贪婪选择保留下优质染色体，加快算法收敛速度。

染色体的新生受随机选取父代染色体的社会条件和整个社会环境所共同影响。

式中：j1和j2—新生染色体的两个随机选取的维度；rj—[0，1]内均匀分布的随机数；Rj—决策变量在第j维范围内随机产生的变异值；Ps—分散概率；Pa—关联概率。

新生染色体的生与死由其社会适应能力决定，具体描述如下：（1）组内有一或多条染色体比新生染色体差，则新生染色体生而最差的染色体死；（2）组内无染色体比新生染色体差，则新生染色体死。

4.5 变异

变异操作为GA中增加种群多样性的步骤，有利于改善算法的早熟收敛。在车间调度领域常用的变异操作为：互换操作、逆序操作、插入操作等。采用的是互换变异，按照变异概率随机交换父代染色体除精英选择保留到子代种群外的染色体两不同位置上的基因。

GA—COA混合算法流程，如图1所示。

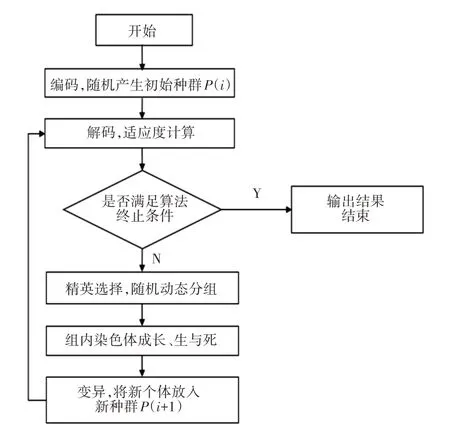
图1 GA—COA流程图Fig.1 GA−COA Flow Diagram

5 实例分析

利用一个标准算例，对所提出的MRFJSP 模型和GA—COA混合算法进行验证，在MATLAB中编程实现。根据文献[14]中提出的（6×10）FJSP 算例（工件数6，机床数10）的基础上加入仓储和运输（AGV），设机床间的距离相等，AGV在各机床间的运输时间为1，则工件运输时间，如表3 所示（0 代表仓库，1−10 代表机床号），工件的加工时间，如表4所示。

表3 工件运输时间表Tab.3 Workpiece Transport Schedule

表4 工件加工时间表Tab.4 Workpiece Processing Schedule

根据文献[9−12]，GA、COA及GA—COA参数设置，如表5所示。

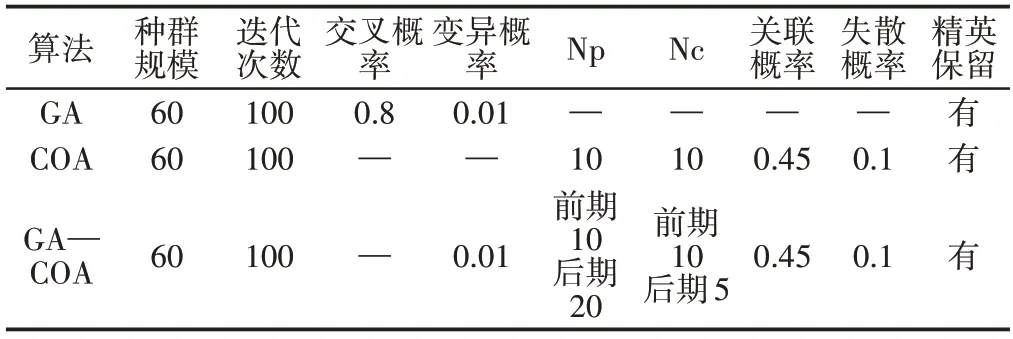
表5 参数设置Tab.5 Parameter Setting

GA、COA 及GA—COA 三者运行100 次最优结果，如图2 所示。对比可见COA 的寻优能力是强于GA的，GA—COA 混合算法是优于前两者的。GA的交叉操作增强了种群的多样性，且引入随机动态分组加快了种群收敛并改善了算法的操作性，表明GA−COA混合算法在MRFJSP求解中的优越性。

图2 迭代结果对比图Fig.2 Comparison Diagram of Iteration Results

获得最优的调度甘特图，如图3所示。最优调度周期为162。柔性作业车间中工件初始存储于仓库中，由AGV运输至相应机床的线边库中；工件在机床间的运输时间是不确定的，需要单独考虑；加工完的工件由AGV运回仓库，当最后一个工件的回库表明整个加工流程的完结。因此，将仓储和运输考虑到FJSP中是必要的，为精细化调度做出更好的指导参考。

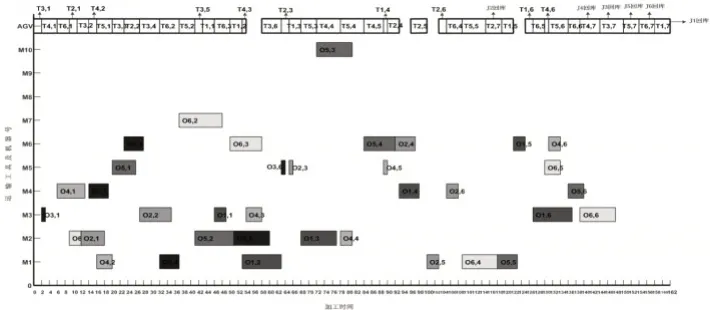
图3 调度甘特图Fig.3 Schedule the Gantt Chart

6 结论

将仓储和运输两个环节考虑到FJSP中，对该MRFJSP 进行建模，并设计了一种混合算法用于求解该问题。GA—COA混合算法将COA中多组结构、组内郊狼成长、生与死代替GA中的交叉操作，并加入随机动态分组和精英保留策略，增强混合算法的操作性能，避免算法陷入早熟收敛的不足。通过对比求解结果，证明混合算法在求解MRFJSP中的优越性。另外，仓储作为工件的存储装置，是生产环节不可忽视的一重要环节，而运输时间影响着整个生产过程，因此将仓储和运输考虑到FJSP中是必要的、更贴近实际情况的。