地月空间星地双向单程测量高精度模型

刘 通，陈 浩，郭鹏斌

(1. 中国科学院太空应用重点实验室，中国科学院空间应用工程与技术中心，北京 100094；2. 北京跟踪与通信技术研究所，北京 100094)

0 引 言

使用双程单向测量(Dual one way ranging，DOWR)量相减进行钟差估算可以将传播路径上的公共误差抵消，相加计算距离可以将两端时钟的噪声基本抵消，从而实现更高精度的星地或星间的时间比对和距离测量。该方法在科学探索及工程项目上得到了广泛应用。由美国宇航局，德国宇航局和德国波茨坦地学中心等机构合作研制，于2002年发射的重力回溯及气候实验(Gravity recovery and climate experiment，GRACE)项目使用K/Ka频段的DOWR载波相位测量实现了两相距约220 km的低轨卫星之间的微米级相对距离测量和优于1 μm/s的距离变化率测量，用于高精度监测地球重力场变化等[1-2]。由美国宇航局等机构研制，于2011年发射的重力回溯及内部结构实验室(Gravity recovery and interior laboratory，GRAIL)项目使用Ka频段的DOWR载波相位测量实现两相距约200 km的绕月卫星之间的相对距离高精度测量，精确探测月球重力场以判断其内部构造[3]。Turyshev等[3]在广义相对论框架下，给出了使用GRAIL任务Ka频段的DOWR载波相位测量量进行绕月卫星星间1 μm精度相对距离测量模型和1 μm/s精度距离变化率测量模型。同时GRAIL任务还使用S频段的DOWR测量量实现星间的高精度时间比对和绝对距离测量[4]。北斗导航卫星使用DOWR码伪距星间测量实现厘米级星间测距及优于1ns的星间时间同步，为对地面站不可见的导航卫星提供了另一种高精度时间同步技术途径[5-6]。黄飞江等[7]提出一种基于最小二乘拟合的星地动态双向时间同步与测距算法。MEO卫星与地面站之间的DOWR仿真数据处理结果表明，使用该算法计算的星地时间同步精度优于 3 ns，测距精度优于 3 m。空间站原子钟组(Atomic clock ensemble in space, ACES)是欧空局的空间时钟任务，该任务计划将其建立的超高精度时频标准通过Ku频段的DOWR以ps级的精度传递给多个地面站[8]。我国空间站实验舱上搭载的精密时频柜也计划采用K～Ka频段DOWR测量方式实现超高精度和稳定性的星地时间比对[9-10]。卫星双向时频比对(Two-way satellite time and frequ-ency transfer，TWSTFT)是利用地球同步卫星转发两个实验室的时间信号，两站同时进行信号发射和接收，进行双向时间、频率信号传递的技术，是目前国际上实现协调世界时(Universal time coordinated，UTC)所使用的高精度时间比对技术之一，其原理也可视为一种特殊的DOWR测量方式[11]。

上述参考文献使用DOWR进行高精度时间同步或距离测量的场景均为在同一个自然天体的两颗卫星之间开展测量，如GRACE任务，北斗星间链路和GRAIL任务，或是绕地球航天器和地面站之间进行测量，这类问题的DOWR模型在地惯系或月惯系中建立即可。论文讨论分析使用DOWR测量方式进行绕月卫星和地面测站之间的高精度时间比对和距离测量，探索支持未来中国载人登月等星际任务的高精度时间比对技术及地月空间自主导航技术。基于DOWR技术的地月空间星地时间比对和距离解算应该在太阳系质心天球参考系(Barycentric cele-tial reference system，BCRS)中进行。时间尺度应选择质心坐标时(Barycentric coordinate time，TCB)或质心力学时(Barycentric dynamical time，TDB)。模型中各项量级分析和误差分析基于BCRS系度规和广义相对论理论。模型中不同时间尺度之间的转换需要考虑观者位置的影响。引力时延和相对论频移的建模和误差分析需要考虑多个天体引力场的影响。论文的第一节建立了基于DOWR的地月空间星地时间比对和距离解算模型，并在给定的场景中，分析了模型中各项量级。第二节在给定场景下，讨论了时差和距离单次解算模型中各因素引入的误差量级，包括卫星定轨精度，大气延迟修正误差，引力时延修正误差和相对论效应修正误差等因素。第三节考虑星钟和地面站时钟噪声，测量噪声，系统收发时延等因素进行符合给定场景的DOWR数据仿真，并考虑卫星位置和速度估算误差，与仿真模型不同的动力学模型，地面站气象参数的测量误差等因素对仿真数据进行处理分析，计算星地瞬时钟差和距离，并对结果进行讨论分析。第四节为全文总结。

1 地月空间DOWR高精度模型

1.1 双向单程测量

在图1所示的测量场景中建立基于双向单程伪距测量量的星地时差与距离解算模型。对于上行链路，卫星测量到的伪距为ρup；对于下行链路，地面站测量到的伪距为ρdown。伪距值为信号真实传播时间与星地时钟误差之和。其中，信号真实传播时间为系统收发时延和信号从天线相位中心发出到接收方的天线相位中心的飞行时间之和；时钟误差为相对论频移引入的钟差及钟本身不稳定性和不准确性引入的钟差两部分之和。上下行伪距表达式分别为，

图1 星地双向单程测量Fig.1 Dual one-way ranging

(1)

式中：c=299792458 m/s为光速；T12=t2-t1表示信号于t1从地面站天线相位中心发出，至t2时刻到达卫星天线相位中心飞行总时间；T34=t4-t3表示信号于t3从卫星天线相位中心发出，至t4时刻到达地面站天线相位中心飞行总时间。T12和T34均包括大气折射延迟项，引力时延，星地相对运动时延项等。Dge(t),Dsr(t),Dse(t),Dgr(t)分别表示t时刻地面站发送时延，卫星接收时延，卫星发送时延和地面站接收时延。Δτs(t)和Δτg(t)分别表示星载时钟和地面站时钟在t时刻的由于其不稳定性和不准确性引入的钟差。Crel_up和Crel_down分别表示上行和下行链路中相对论频移修正项。

1.2 地月空间DOWR高精度模型

论文的时间尺度选择秒长和国际原子时(International atomic time，IAT)秒长相同的TCB，记为t。为了在建立模型时给出定量分析，给出如下场景约束，

1) 用来解算单次星地钟差和瞬时距离的一对伪距值的接收时刻相同；

2) 绕月航天器在距离地心2.8×105～4.8×105km中的空间中运动；

3) 绕月航天器在BCRS系中的运动速度大小为28～32 km/s；

4) 上下行链路均工作在K频段中23～27 GHz；

5) 地面站时钟为和UTC高精度时间同步和频率同步的高性能原子钟，钟差估算精度为ns级，在卫星任务期间，频率准确度优于5×10-12，频漂优于5×10-15/86400 s；

6) 星载原子钟频率准确度在卫星任务期间优于5×10-9，频漂优于3×10-13/86400 s，星地钟差Csg(t)=Δτs(t)-Δτg(t)可以通过地面站主动授时等手段控制在6×10-4s之内，校时间隔小于一天；

7) 地面站系统收发时延可能为负值，绝对值小于300 ns，星上系统收发时延均为正值，且小于30 ns。

Dsha_up+Dother_up

(2)

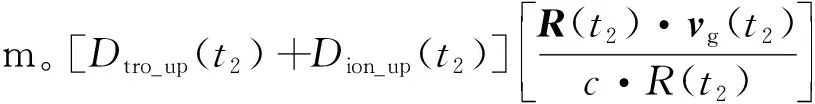
(3)

Crel_up和Crel_down值相近，符号相反。卫星固有时和坐标时之间频移，协调世界时和坐标时之间频移均大于1.4×10-8，小于1.6×10-8，所以Crel_up和Crel_down之和为10 ns量级。用来解算星地钟差和瞬时距离的一对伪距值的接收时刻相同，即τs(t2)+Dsr(t2)+Δτs(t2)=tUTC(t4)+Dgr(t4)+Δτg(t4)。且卫星固有时和坐标时之间频移，协调世界时和坐标时之间频移均小于1.6×10-8，系统收发时延小于300 ns，星地钟差控制在6×10-4s之内。所以在式(3)计算时，认为τs(t2)=tUTC(t4)为上下行伪距接收时刻，引入的Crel_up和Crel_down计算误差小于10 ps，可以忽略。将上行和下行的伪距测量量表达式相减，忽略小于10 ps的项及多径效应影响，记T23=t3-t2。地面站和星上原子钟的天频漂值均远小于其频率准确度，所以在短时间内，星地钟差变化由二者频率准确度决定，呈线性关系，得

Dge(t1)-Dsr(t2)+Dsha_down-Dsha_up+

[Dion_down(t4)-Dion_up(t2)]+[Dtro_down(t4)-

Dtro_up(t2)]+[tUTC(t1)-t1]+[tUTC(t4)-t4]-

[τs(t2)-t2]-[τs(t3)-t3]-

(4)

式(4)为星地时差解算模型。这里星地时差为由于星载时钟和地面站时钟的不稳定性(通常以Allan方差或Hadamard方差给出时钟的稳定性指标)和不准确性(包含初始同步钟差，频差，频漂)引入的误差，不包含相对论效应影响。将上行和下行的伪距测量量表达式相加，整理得，

[Dge(t1)+Dsr(t2)]-(Dsha_down+Dsha_up)·

[Dion_down(t4)+Dion_up(t2)]-[Dtro_down(t4)+

Dtro_up(t2)]+[tUTC(t1)-t1]-[tUTC(t4)-t4]-

[τs(t2)-t2]+[τs(t3)-t3]-[Δτs(t2)-

Δτs(t3)]-[Δτg(t4)-Δτg(t1)]+

(5)

式(5)为星地距离解算模型。从星地钟差及距离解算模型中可以看出，钟差和距离的解算并未完全解耦。钟差的表达式中含有和瞬时距离相关的Sagnac项。距离计算表达式中存在钟差项-[Δτs(t2)-Δτs(t3)]-[Δτg(t4)-Δτg(t1)]。在给定的场景下(绕月航天器距离地心2.8×105～4.8×105km，用来解算单次星地钟差和瞬时距离的一对伪距值实测接收时刻相同)，该钟差项表示星载原子钟和地面站原子钟频差之和的0.9～1.6倍。地面站钟频率准确度优于5×10-12，星载钟频率准确度优于5×10-9，测量时星地距离约4.8×105km，忽略钟差项，引入的瞬时距离计算误差约1.2 m。若通过对钟差的多次估算，可以使用最小二乘或卡尔曼滤波等方法以3×10-10的精度估算星钟频率准确度，则对钟差项修正后，引入单次瞬时距离估算误差约为7.2 cm。

1.3 时间比对和距离解算模型各项量级分析

为了更好的定量分析，除了在1.2节中列出的7条场景约束，给出以下约束条件，

1) 地面站气象条件在3 s左右时间间隔内变化小，对流层时延变化小于200 ps；

2) 依据精密定轨结果，卫星姿态精度及相位中心偏移修正综合计算给出的星载天线相位中心位置误差小于10 km，速度误差小于10 cm/s；

3) 地面站天线相位中心在BCRS系中的位置误差和速度误差主要来源于地心位置误差和速度误差；

4) 地心位置误差小于1 km，速度误差小于10 cm/s；

5) 结合卫星平台搭载载荷的外形设计，太阳能帆板及星载天线安装位置，地面站周围环境及天线不遮挡情况，采取安装抗多径天线等措施，分析得出多径引起的伪码误差可以有效得到控制，认为多径效应引入的伪距测量误差小于1 m。

总结1.2节讨论分析，表1给出式(4)和式(5)右侧各项量级。

表1 星地钟差和距离解算中各因素绝对值量级Table 1 Absolute values of each factor in the calculation of satellite-ground time comparison and instantaneous distance

2 时差和距离单次解算误差分析

依据式(4)和式(5)估算星地时差和瞬时距离的精度取决于，计算式中各项依据的具体模型精度和数据质量引入的误差，如测量误差，系统收发时延标校误差，相对论效应计算误差，卫星定轨精度，大气延迟修正误差等因素， 1.2节分析了钟差项估算精度对星地瞬时距离解算的影响。本节对其他因素引入的误差量级进行讨论。

2.1 测量误差

上行和下行伪距测量误差分别记为σρup和σρdown。则该项引入星地钟差估算最大误差为，

(6)

其中，当σρup=σρdown=0.5m时，引入的星地钟差计算误差σCsg≈1.67ns，星地瞬时距离的计算误差σR≈0.5 m。可以通过提高码片率，降低载噪比等来降低测量误差。

2.2 收发时延标校误差

在设备工作环境稳定的情况下，地面站系统发送时延，接收时延，卫星发送时延和接收时延标校的误差分别记为，σDge,σDgr,σDse和σDsr，认为卫星收发时延测量误差和地面站收发时延测量误差相互独立，则该项引入星地钟差估算最大误差为

(7)

收发时延的标定结果随工作环境温度等条件变化而改变，美国国家标准与技术研究院学者实验结果表明，其进行实验的地面站设备发送时延温漂系数约为(-50±10) ps/℃，接收时延温度系数约为(-150±30) ps/℃[13]。在短时间内，温度基本不变，若σDge=σDgr=σDse=σDsr≤3 ns，则引入的σCsg≤4.3 ns,σR≤1.28 m。长时间情况下，星载或地面站设备由于工作环境如温度变化会引入额外的误差，如一天时间内，星载系统工作温度变化可达30 ℃，若温漂系数为-200 ps/℃，则接收时延变化约为6 ns。对于地面站可通过定时标校，温度控制或测量实时温度，然后对测量数据进行温度补偿来精确修正。国家授时中心和日本通信综合研究所联合进行的卫星双向时间比对实验的误差分析显示，即使去掉温度影响，设备收发时延误差仍是该时间比对实验中的最大误差源[14]。

2.3 引力时延修正项及其误差

相对论效应计算误差包括引力时延修正误差和时间系统转换中的计算误差。参考文献[15]中引力时延的表达式，计算太阳及太阳系八大行星，冥王星和月球引起的引力时延。结果表明，除了太阳和地球，其他天体引力场带来的引力时延最大值均小于5 ps。所以计算时仅考虑太阳和地球引力场带来的引力时延。二者的最大值分别小于31.69 ns和250 ps。引力时延的计算误差主要由卫星位置误差引入。当卫星位置误差为10 km，引力时延修正误差小于10 ps。在星地钟差计算中上下行链路的引力时延相减，且二者数值基本相同，其引入的误差可忽略。在星地距离计算中上下行链路的引力时延相加，考虑模型中忽略月球等天体引力场影响带来的误差等，星地距离计算误差小于5 mm。

2.4 时间系统转换中的计算误差

相对论效应修正项式(3)中各项具体表达式为，

(8)

(9)

略去的高阶项ο(1/c4)为1×10-16量级，经过上述分析，本文模型中Uc为卫星在太阳，地球和月球引力场中的引力势之和。使用JPL行星星历对应的地球时间星历实现UTC到TCB之间的转换，地球时间星历项的准确度为0.1ns量级[16]。

2.4.1UTC和TCB转换计算误差

(10)

式中：xE和vE为地心在BCRS中的位置矢量和速度矢量。式(10)右侧括号中的相对论频移积分项引入的钟差计算误差在2.4.2小节中讨论，这里仅分析其他项，可得

(11)

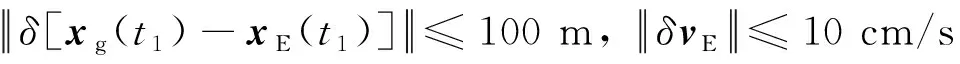
分析星地瞬时距离解算中时间系统转换中的计算误差，式(5)中和其相关项为

t2]+[tUTC(t1)-t1]-[tUTC(t4)-t4]}

(12)

相对论频移积分项引入的误差在2.4.2节中讨论，分析其他项影响，有

(13)

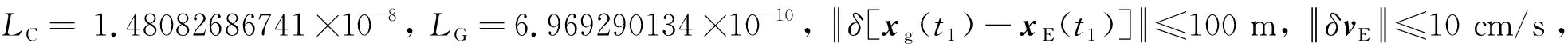
2.4.2相对论频移积分计算误差

由式(10)可以得到相对论频移积分计算误差引入的钟差计算误差为

(14)

相对论频移积分计算误差引入的星地瞬时距离计算误差为

(15)

综上可得，在给定的场景约束下，时间系统转换和星地相对运动项计算误差引入星地时差中的计算误差小于4.19 ns。时间系统转换误差引入星地瞬时距离计算误差小于0.21 cm。

2.5 星地相对运动修正误差

2.4.1节中讨论了星地相对运动修正误差对星地时差计算误差的影响。这里分析星地相对运动修正误差对星地瞬时距离计算误差的影响。卫星位置和卫星速度存在较大的误差，二者主要通过式(5)中Sagnac项的前两项引入星地距离计算误差，即

(16)

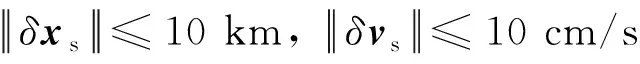
2.6 大气延迟修正误差

大气延迟修正误差包括对流层延迟修正误差和电离层延迟修正误差。对于工作在K波段等频率较高的信号，对流层延迟包括对流层色散延迟和对流层非色散延迟，其中前者一般小于10 ps量级，ACES的微波链路使用海量实测数据拟合计算得到多测站的对流层色散延迟经验公式，来对此项进行修正[17]。下文讨论对流层非色散延迟与电离层延迟修正模型与修正误差。

2.6.1对流层延迟修正误差

对流层延迟修正模型为

Dtro_up=mdry(φ)zdry+mwet(φ)zwet

(17)

式中：zdry和zwet分别为干延迟分量和湿延迟分量的天顶延迟修正模型。mdry和mwet分别为干延迟分量和湿延迟分量的映射函数。φ为观测仰角。天顶延迟修正模型和映射函数模型均有多种。论文认为测站在中纬度低海拔地区，选择Hopfield模型作为干延迟分量和湿延迟分量的天顶延迟模型；mdry选择CFA-2.2模型，即Davis模型，mwet选择Chao模型[18]。文献[19]考察了在不同季节平稳大气环境下多种对流层延迟修正模型的修正误差，其中对中纬度低海拔地区，仰角大于10°的条件下，采用论文选择的模型组合得到对流层延迟修正平均误差较小，约17 cm。气象条件的测量误差也会引入对流层延迟修正误差，如文献[19]中提到的，在相对湿度75%，温度0°～30°的气象条件下，天顶方向的延迟量对表面大气压，温度和相对湿度的敏感系量级分别为2 mm/hPa，5～20 mm/℃，1～3 mm/%。所以，气象条件的精确测量是获得高精度天顶方向延迟修正的必要条件之一。另外当气象条件变化较快时，对流层延迟中的湿延迟分量不易精确估计。结合多篇参考文献，对中纬度低海拔地区，气象参数测量精确(表面大气压，温度和相对湿度测量误差分别为0.3 hPa，0.5 ℃，2%)，在一般气象条件下，采取论文选择的组合模型得到的对流层延迟修正误差小于1 m[18-21]。

由式(4)，在星地钟差计算中，上下行链路的对流层延迟相减，认为在信号往返1.8～3.2 s的时间间隔内，气象条件变化极小，且对于绕月卫星的观测，上行和下行仰角差值非常小，一般情况下带来的对流层时延之差小于200 ps。使用模型修正的误差可能大于实际上下行对流层时延差，所以在时差解算中忽略对流层延迟项，引入的误差为10 ps量级。由式(5)，在瞬时距离计算中，上下行链路的对流层延迟相加。认为上下行对流层延迟修正误差并不相互独立，则引入星地距离估算误差小于1 m。

2.6.2电离层延迟修正误差

电离层延迟修正模型使用经典电离层延迟模型。当载波频率为23 GHz，模型中f-3项带来的电离层时延小于1 ps，所以模型仅考虑f-2项，模型表达式为[22]

(18)

其中，f1和f2分别为上行和下行链路载波频率。Iup和Idown分别为上下行路径天顶方向总电子量。其建模方法有多种，如GPS系统采用的8参数Klobuchar模型，Galileo采用的NeQuick模型，其在全球中纬度地区可以实现50%左右及以上的修正精度。F为倾斜因子，其表达式为[23]

(19)

式中：Re为地球半径；H为电离层薄层高度，取400 km；取f1=23 GHz,f2=27 GHz,Iup和Idown最大约100TECU=1018/m2，则天顶方向上时延最大约为Dion_up≈254 ps,Dion_down≈184 ps。在仰角大于10°时，F<4倾斜路径上的电离层延迟量小于天顶方向的4倍。在钟差计算中忽略电离层延迟修正项，带来的钟差误差约小于140 ps。若上下行总电子量估算误差均为50%，则倾斜方向的大气延迟修正误差引入的星地钟差计算误差最大约为316 ps。使用模型修正的误差可能大于实际上下行电离层时延差，所以在钟差计算中忽略电离层延迟修正。在星地距离计算中电离层延迟修正项小于0.30 m。若上下行总电子量估算误差均为50%，倾斜路径上引入的距离估算误差小于0.13 m。也可以使用双频电离层消去法处理电离层延迟。

2.7 误差量级总结

除了在2.2节和2.3节中列出的12条场景约束，给出以下约束条件。表2在此基础上，给出式(4)和式(5)各项建模方法及引入的误差量级。

表2 星地钟差和距离解算中各因素建模或处理方法引入的误差量级Table 2 Errors of satellite-ground time difference and instantaneous distance estimation caused by the modeling or processing method of each factor

1)通过对钟差的多次估算，可以以3×10-10的精度估算星钟频率准确度；

2)上下行伪距测量精度小于0.50 m；

3)采取定时标定手段，地面系统收发时延误差均小于3.0 ns，且收发时延误差变化有一定的相关性；卫星发射前标定收发时延，在轨测量工作环境温度进行温漂补偿，收发时延误差均小于5.0 ns，且收发时延误差变化有一定的相关性，收发时延差值经过温漂补偿后，引入钟差计算误差小于4.0 ns。

4)卫星姿态测量精度优于0.1°；

5)卫星观测仰角大于10°；

6)地面精测卫星天线相位中心和星载原子钟相对卫星质心的位置误差在mm级。

表2显示在上述列出的场景约束下，星地钟差计算误差小于7.6 ns，星地瞬时距离计算误差小于2.4 m。若地面站时钟钟差估算误差小于10 ns，则卫星钟差计算误差小于12.3 ns。系统收发时延误差是影响星地钟差和瞬时距离估算精度的主要因素之一。

3 仿真数据处理与分析

3.1 测量数据仿真

为校验星地钟差和星地距离解算模型的精度，这里使用解算模型处理仿真数据，并对结果分析讨论。仿真模型设置，

1) 星钟参数，初始钟差0.5 ms，初始频差5×10-10，频漂(天漂移率)为3×10-13。原子钟的稳定性指标以Hadamard标准差给出，满足≤5×10-12/(1 s)，≤2×10-12/(10 s)，≤5×10-13/(100 s)，≤2×10-13/(1000 s)，≤1×10-13/(10000 s)，≤1×10-13/(24 h)，仿真时取稳定性指标临界值。

2) 地面站时钟参数，准确度参数，初始钟差5 ns，初始频差2×10-13，频漂(天漂移率)为2×10-15。稳定性指标以Allan标准差给出，≤2×10-13/(1 s)，≤6×10-14/(10 s)，≤9×10-15/(100 s)，≤5×10-15/(1000 s)，≤3×10-15/(1 h)，≤2×10-15/(10000 s)，≤2×10-15/(24 h)，仿真时取稳定性指标的临界值。

3) 测量误差，伪距测量噪声为均值为0，方差为0.5 m的白噪声。

4) 收发时延，地面站系统收发时延噪声设置为均值300 ns，方差为3 ns的白噪声；星上系统收发时延噪声设置为均值30 ns，方差为5 ns的白噪声。

5) 绕月航天器轨道类型选择共振比为2∶1的远距离逆行轨道(Distant retrograde orbit，DRO)，卫星距离地心2.8×105～4.8×105km,距离月心7×104～1×105km，在BCRS系中的运动速度为28～32 km/s。

6) 动力学模型设置，选择太阳质点模型，地球引力场非球形50×50 EIGEN_6C4，月球非球形引力场非球形50×50 GRGM1200B，光压模型参数，面质比0.002 m2/kg，积分器选择RK4，积分时间为10 s。

7)地面站选择北京密云站，设置经纬度高程(116.976°E, 40.368°N, 160.00 m)。

8)仿真时段选择卫星对地可见且仰角大于20°的时间段。

9)对流层延迟建模，区别于数据处理时3.5.1节中使用的模型，天顶方向延迟模型和映射函数模型均采用Saastamoinen模型。

10)电离层延迟建模，采用文献[19]中经典电离层延迟模型，考虑其中的f-2项，忽略地磁场影响，倾斜因子依据式(19)给出。

11)行星星历选择DE430。

3.2 仿真数据处理

仿真数据处理时，相关数值设置如下:

1)初始位置误差10 km，初始速度误差10 cm/s。

2)收发时延设置，地面站系统收发时延取300 ns，星上系统收发时延取30 ns。

3)设置与仿真程序中不同的动力学模型，选择太阳质点模型，地球引力场非球形20×20 GGM05C，月球非球形引力场非球形20×20 GRGM900C，面质比0.002 m2/kg，积分器选择RK4，积分时间为10 s。

4)地面站位置误差小于100 m，速度确定误差小于1 cm/s。

5)表面大气压，温度和相对湿度测量误差分别为0.3 mbar，0.5 ℃，2%。

6)行星星历选择DE421。

分析处理时长3 h的DOWR仿真数据，图2给出了星地钟差真实值与星地钟差估算结果，估算误差如图3，其均方根误差为6.90 ns(仿真数据中认为地面站的收时延和发时延误差变化负相关)。得到星地瞬时距离估算误差如图4所示，其均方根误差为2.03 m(仿真数据中认为地面站的收时延和发时延误差变化正相关)。校验了论文第二节中的定量分析结论。其均方根误差略小于理论分析的原因有两个。第一个原因为，在第二节进行误差定量分析中，仅考虑运动学模型，认为轨道在径向，切向和法向的误差分量基本独立，没有动力学模型约束；而在仿真数据处理中，考虑了动力学模型对运动学参数误差传播的约束。第二个原因为，表2给出的电离层和对流层引入的误差为最低仰角10°的误差，仿真数据长3小时，仰角为70°左右，且仿真中气象条件变化平稳，所以大气延迟引入的误差较小。

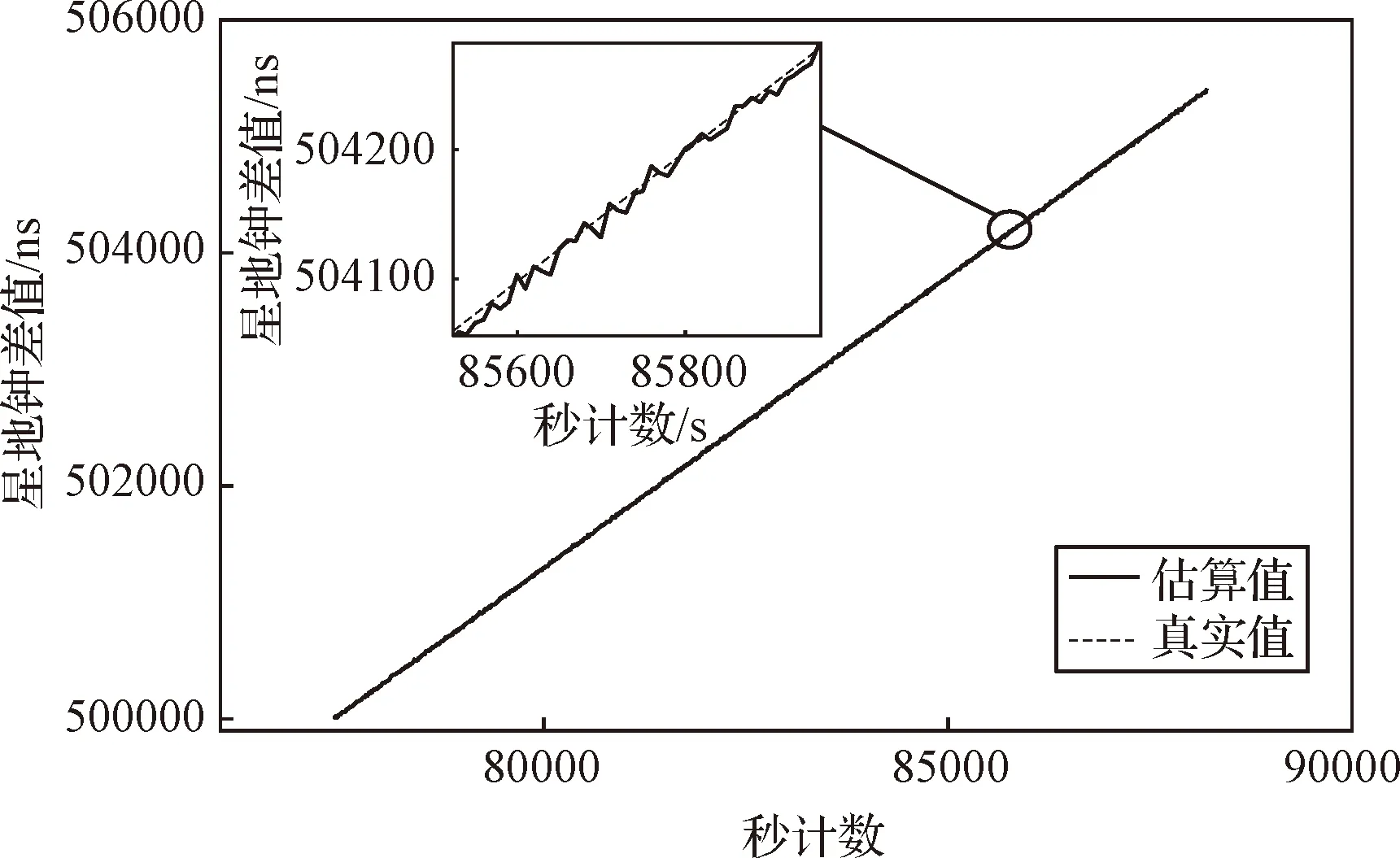
图2 星地钟差估算结果Fig.2 Estimation results of satellite-ground clock difference

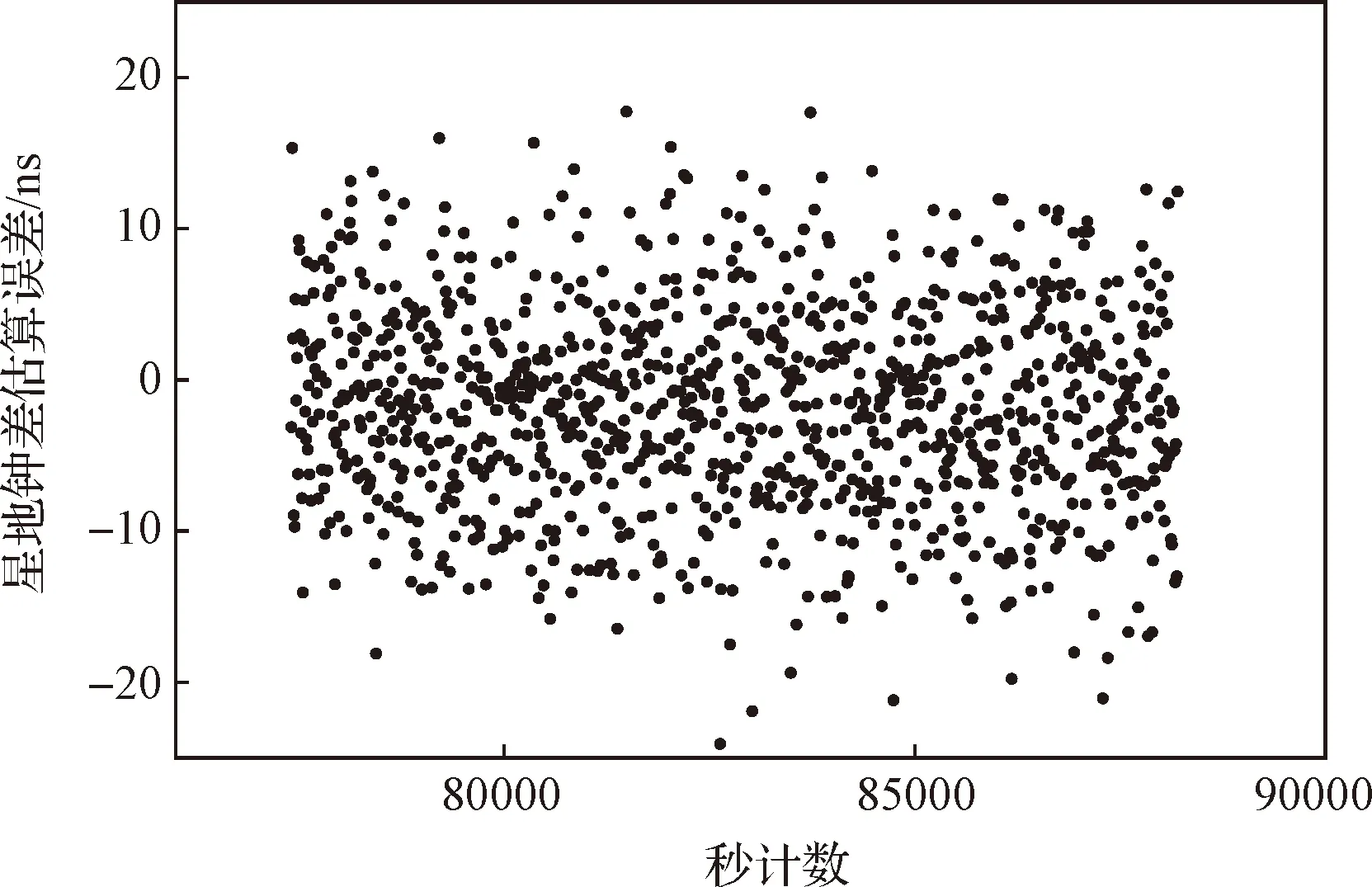
图3 星地钟差估算误差Fig.3 Estimation errors of satellite-ground clock difference

图4 星地瞬时距离估算结果Fig.4 Estimation errors of satellite-ground instantaneous distance

4 结 论

论文考虑系统误差，引力时延，相对论频移，星地相对运动效应，大气延迟等因素的影响，建立了地月空间星地双向单程测量高精度模型。在给定场景下，对模型中各项因素可能引入的误差进行了定量分析。理论分析结果表明，使用该模型进行星地钟差估算误差小于7.6 ns，星地瞬时距离计算误差小于2.4 m。使用该模型处理仿真数据，估算得到的星地钟差均方根误差为6.90 ns，星地瞬时距离均方根误差为2.03 m。仿真实例校验了该模型的有效性和模型误差定量分析结果的准确性。