航天器反应式碎片规避动作规划方法

吴健发，魏春岭，张海博

(1. 北京控制工程研究所，北京 100094； 2. 空间智能控制技术重点实验室，北京 100094)

0 引 言

根据NASA轨道碎片项目办公室的统计，截至2022年3月，编目的空间碎片总数已接近26000个[1]。密集分布的空间碎片对航天器的在轨安全运行造成严重威胁，近年来已发生多起航天器与碎片的交会事件，例如，2021年5月12日，国际空间站在例行检查中发现其机械臂已被未知的空间碎片撞出一个明显的破洞；2022年1月18日，我国清华科学卫星与俄罗斯的宇宙1408卫星碎片发生了一次极危险交会，双方最近距离仅14.5 m。如何使航天器自主、安全地规避规模日渐庞大的空间碎片群，已成为目前各航天大国研究的重要课题。

航天器自主规避技术主要涵盖感知、规划和控制三个层面，其中规划技术基于感知的空间态势，生成航天器的最优规避路径和机动动作，并对姿轨控制系统下达控制指令，在三个层面技术中起“大脑中枢”的关键作用，受到广泛的关注。从目前的文献来看，如果以决策行为模式的角度分类，则相应的规避动作规划方法可分为慎思式和反应式两类方法[2]。慎思式动作规划方法通过对当前/历史状态信息进行逻辑推理的方式实现决策，形式上表现为“状态-估计-预测-建模-规划-动作”的分层串行规划过程，其典型方法为基于预测控制的动作规划方法，即预测有限步长内的威胁状态，基于此优化该时间段内的控制序列，最后执行当前时刻所需控制输入，例如，Weiss等[3]针对航天器交会对接问题，提出一种动态可重构约束的线性二次模型预测控制制导方法，该方法基于测量的相对距离和角度估计航天器状态，进而根据估计信息并结合视野锥、控制器带宽和羽流方向等非线性约束条件，采用二次规划方法求解相应控制量；Li等[4]针对轨道追逃问题，首先采用无迹Kalman滤波算法估计对手的未知信息，进而将估计参数输入基于微分对策的最优逃逸策略中，实现不完全信息条件下的轨道博弈。总体而言，这类方法能取得不错的规划效果，但求解流程比较复杂，各环节累加计算耗时较长，不利于对威胁做出快速反应[2]。

与之相对的是反应式规划方法，即根据一定规则直接基于当前/历史状态信息映射出对应动作，形式上表现为没有“预测”、“建模”等环节的“状态-动作”端到端决策过程，例如文献[5-6]提到的应急机动决策方法。由于空间光照条件复杂，可能会影响航天器探测设备成像的连续性，容易造成空间碎片的漏检[7]。当航天器重新检测到碎片时，二者距离可能已相当接近，必须尽快规划并执行相应的规避动作。相较于慎思式方法，反应式方法在这类场景下可能具有更好的适用性，原因在于反应式方法具有更快的决策速度，有利于对多发、突发、动态的空间碎片群做出及时地响应。然而，由于不存在直接的“预测”和“建模”环节，导致部分基于简单规则的反应式方法因不能充分利用历史和模型信息而产生并不理想的规划效果。

近年来，以深度强化学习为代表的新一代人工智能方法广泛应用于各类复杂系统的优化控制问题，其具有如下优点[8]：(1)引入的深度神经网络一方面能在与环境的交互过程中充分提取历史信息的特征并学习到其中的状态变化规律，实现间接的高质量“预测”，另一方面具备强大的非线性逼近能力，可有效应对高维连续状态-动作空间下的优化控制问题；(2)深度强化学习得到的策略在使用时只需进行一个神经网络的前向传播过程，适用于具有高实时性需求的决策任务。这些优点使得通过反应式规划方法生成高质量的规避动作成为可能，从而吸引了众多学者进行探索，例如，针对离散动作空间，Ge等[9]提出一种可采用深度Q学习的航天器反应式鲁棒轨迹规划方法，可生成针对动态威胁的无碰撞轨迹走廊；在此基础上，一些研究进一步提出面向连续动作空间的深度强化学习方法，其搜索空间更大，求解质量更高，在航空宇航领域目前已应用于无人机机动控制和导弹制导中[10-13]，但对于航天器规避动作规划问题尚缺乏针对性研究。

围绕空间碎片规避任务需求，本文提出一种航天器反应式规避动作规划方法，该方法将一种成熟有效的自然启发式规避动作规划算法：扰动流体动态系统(Interfered fluid dynamical system, IFDS)与目前比较先进的一类深度强化学习算法：双延迟深度确定性策略梯度(Twin delayed deep deterministic policy gradient, TD3)有机结合，并引入优先级经验回放和渐进式学习策略以提升深度强化学习的训练效率，最终面向多发、突发、动态且形状各异的空间碎片群，实现规避机动动作的“状态-动作”端对端快速规划。

1 问题描述

1.1 航天器轨道运动建模

当航天器感知到空间碎片并准备进行规避机动时，记此时处于工作轨道的航天器为参考航天器，位置为o，以o为原点建立LVLH坐标系，ox轴沿参考航天器地心矢径方向；oy轴沿参考航天器轨道面内运动方向；oz轴垂直于参考航天器轨道面，与ox,oy轴构成右手系。在LVLH坐标系下，航天器相对于参考航天器的轨道动力学方程可简化为Clohessy-Wiltshire(C-W)方程：

(1)

式中：X=[x,y,z]T为航天器相较于参考航天器的位置；ω为参考航天器的轨道角速度；u=[ux,uy,uz]T为航天器的轨控加速度，满足有界约束条件|ui|≤umax,i=x,y,z。

1.2 空间碎片群建模

空间碎片或碎片群可用球体或椭球体等效安全包络建模，模型定义如下：

(2)

(3)

注1：航天器对空间碎片的规避是一个包含态势感知、交会预警、规避决策、动作规划、控制执行等多个环节的复杂系统工程[7]，本文聚焦于整个系统工程中的动作规划环节，而对于式(2)中碎片群参数的测定则属于态势感知环节，目前已具有相对成熟的技术方案，且测量精度较高，例如：对于碎片群包络形状参数的测定可采取类似点云数据聚类的思路，这种思路目前已在地外探测[14]、自动驾驶[15]等领域得到广泛应用；对于碎片群的位置速度，可由航天器敏感器自主测定并进行轨道外推，或由航天器与体系化的天基/地基观测系统联合测定，具体方案可见文献[7,16-17]。因此本文假设由感知环节给出的碎片群参数具有较高的置信度。

2 基于扰动流体动态系统的航天器规避动作规划基础算法

本文选取扰动流体动态系统(IFDS)作为规避动作规划的基础算法，该方法原本是一种三维路径规划方法，其模拟了自然界水流的宏观特性，原理是将威胁视为河流中的岩石，将规划的路径视为流水的流线，当流线经过岩石时，根据流体力学理论，岩石会对其施加一个可量化的扰动效应，使水流改变方向从而平滑的绕过岩石。该方法具有如下优点：(1)面对并发、动态威胁时仍具有较高的计算效率；(2)规划路径平滑，便于控制器跟踪；(3)可调参数较少，且物理意义明确。目前该方法已在无人机、水下机器人等自主无人系统中得到应用[11,18-19]，但其在航天领域的应用仍有待进一步探索。由于航天器的运动学特性以及轨道规避任务场景与上述无人系统相比存在较大差异，因此本文对IFDS算法进行了一定的针对性改进，以使其能够规划航天器的轨道规避机动动作u=[ux,uy,uz]T，具体如下：

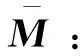
(4)

式中：wk(ΔXk)为第k个包络的权重系数，其取决于航天器与包络表面的距离，距离越大权重系数越小(即产生的扰动效应越小)；Mk(ΔXk)为第k个包络的扰动矩阵。wk(ΔXk)和Mk(ΔXk)的公式如下：

(5)

(6)

式中：I3为三阶单位吸引矩阵，引导航天器沿原有轨迹运行；第二项和第三项分别为排斥矩阵和切向矩阵；ρk和σk分别为对应包络的排斥反应系数和切向反应系数，决定航天器的规避时机(值越大，时机越早)；nk(ΔXk)为径向法向量，垂直于包络向外；tk(ΔXk,θk)为单位切向矩阵，其可分解为垂直于nk(ΔXk)且相互垂直的两个向量tk,1(ΔXk)和tk,2(ΔXk)：

(7)

由tk,1(ΔXk)和tk,2(ΔXk)所组成切平面内的任意单位切向量可表示为：

(8)

式中：θk∈[0, 2π]为任意切向量与tk,1(ΔXk)的夹角，称为切向方向系数，决定规避方向。

以tk,1(ΔXk),tk,2(ΔXk)和nk(ΔXk)分别为x,y和z轴建立新的直角坐标系，由该坐标系到坐标系Dx′y′z′下的坐标转换矩阵P如式(9)所示，则t′k可通过P转化为tk(ΔXk)，即tk(ΔXk)=P·t′k。

(9)

(10)

在此基础上，考虑到输入有界约束，航天器的可达轨控加速度可按如下步骤解算：

(11)

其中，ΔTc为动力学计算采样时间步长。

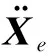
(12)

最终基于输入有界约束对uc进行限幅处理，得到实际可达的轨控加速度u。

3 基于双延迟深度确定性策略梯度的反应式动作规划方法

3.1 总体设计

图1 反应式规避动作规划方法的总体架构Fig.1 Overall framework of the reactive collision-avoidance action planning method

3.2 训练机制

TD3[20]改进自深度确定性策略梯度[21](Deep deterministic policy gradient, DDPG)算法，是目前比较先进的一类面向连续状态/动作空间的深度强化学习算法。DDPG基于动作-评价机制，利用深度神经网络逼近价值函数和确定性策略，可视为深度Q学习(Deep Q-learning)与动作-评价机制的结合。然而，由于DDPG在价值估计过程中存在不可避免的噪声，因此常出现价值过高估计现象，导致算法获得较差的策略。为降低过估计的效果，借鉴van Hasselt等[22]提出的双Q学习(Double Q-lear-ning)思路，TD3采用了两套评价网络估计价值函数，并使用动作网络延迟更新和目标动作网络平滑正则化等操作来进一步提高算法的收敛性。

TD3中一共使用了6个神经网络，动作现实网络，动作目标网络，以及2个评价现实网络和2个评价目标网络，结构如图2所示。本文所构造的网络结构如图3所示：动作网络由输入层(INPUT)、全连接层(FC)、线性整流单元层(ReLU)和双曲正切层(tanh)组成，仅包含观测量o的输入通道；评价网络则包含观测量o和动作量a两个输入通道，由INPUT、FC、ReLU和叠加层(ADD)组成；括号中的数字表示FC层的节点数。

图2 TD3的结构Fig.2 Structure of the TD3

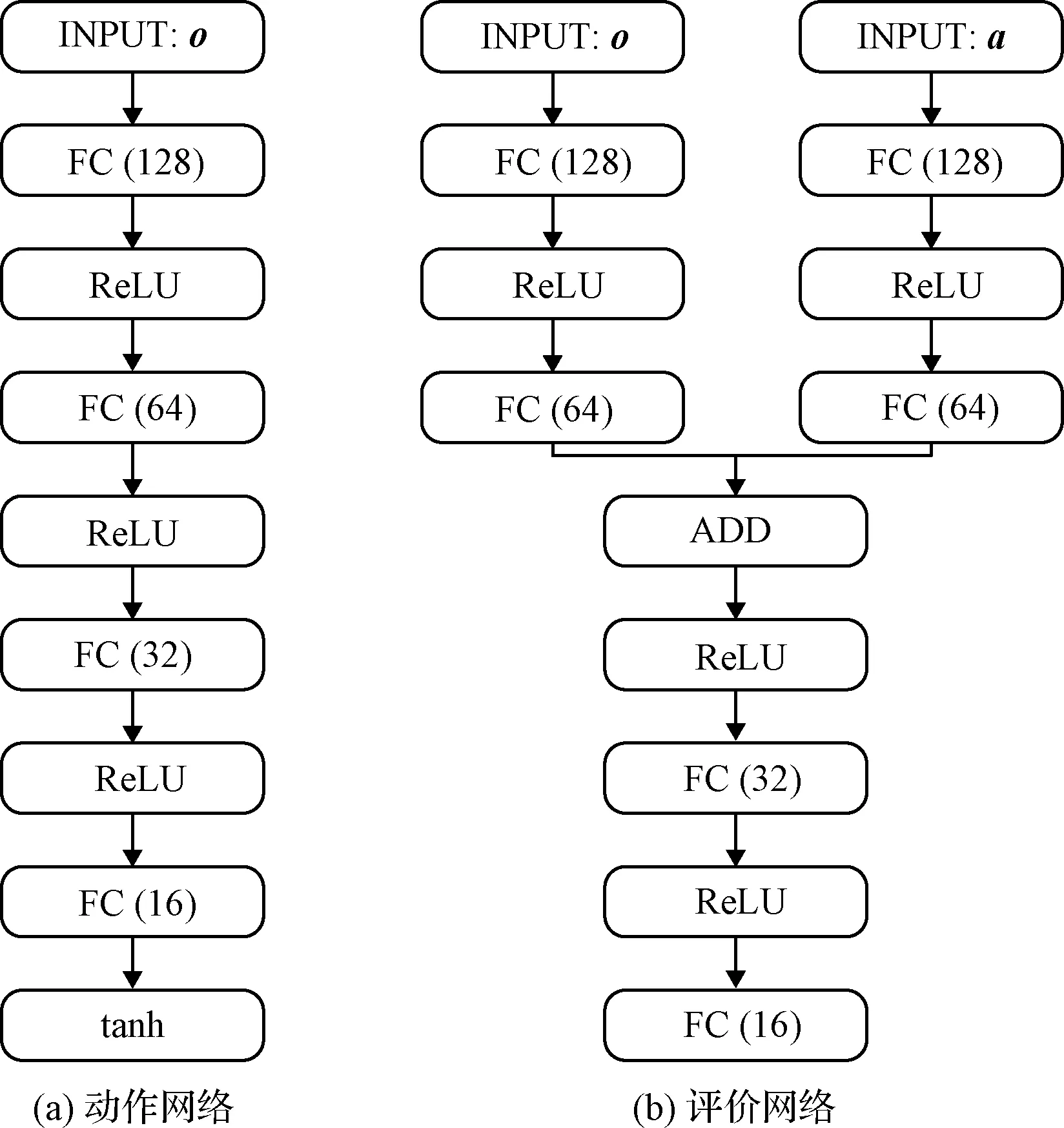
图3 动作和评价网络结构Fig.3 Structures of actor and critic networks

观测量o和动作量a定义如下：

(13)

a=[ρ,σ,θ]

(14)

式中：o中各量分别表示航天器到包络表面的距离，以及航天器与包络中心的相对位置和速度；a为包络对应的IFDS规划参数组合。

针对航天器规避动作规划问题，相应训练机制设计如下：

1) 动作现实网络根据从训练环境中获得的观测量ot选择一个动作输出at，并与随机噪声ϑt叠加以增强探索性，上述过程可表述为：

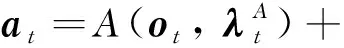
(15)

2) 在训练环境中执行at，计算对应的奖励函数rt并更新观测量ot→ot+1。在此基础上，将状态转移过程{ot,at,rt,ot+1}存入经验池中。

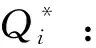
(16)

式中：μ为折扣因子；ε为截断的随机噪声，用于目标策略平滑。

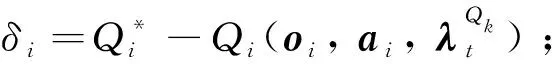
(17)

式中：Pi为采样概率；α∈[0, 1]用于调节优先程度；FRK(|δi|)表示|δi|由大到小的排名数。

最后，由于基于优先级的经验回放引入了偏差，改变了样本的采样频率，因此需要引入重要性采样更新样本计算梯度时的误差权重i：

(18)

式中：β用于控制校正程度。

(19)

(20)

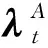
(21)

式中：τ为软更新平滑因子。然后循环跳转至步骤1。

当循环数达到最大值T或满足终止条件时，更新回合数，重置训练环境，直至最大回合N时结束训练，并提取动作网络用于在线反应式动作规划。通过上述迭代过程，智能体可以根据自身与训练环境的交互不断调整网络参数以增强自身性能。

3.3 基于渐进式学习策略的训练环境建模方法

基于深度强化学习的动作规划方法需要智能体与训练环境不断交互以提升自身策略水平。为实现高效交互，提升训练效果，必须对训练环境进行合理设计。针对此需求，本文引入渐进式学习策略，提出如下可适配IFDS动作规划算法的、具有规范化设计步骤的训练环境建模方法：

1) 设计如式(22)的环境重置条件Φ，当满足条件Cond1、 Cond2或Cond3之一时，触发重置条件。

(22)

式中：Cond1表示航天器进入包络的后半球区域(即Cond1,a)，且按进入时双方的位置速度推演，一定步长Ω内不会出现Γ(ΔX)≤1(即Cond1,b)的情况(可判定航天器已脱离危险)；Cond2表示航天器与包络发生接触的情况；Cond3表示达到最大循环数的情况。

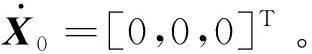
3) 在环境中设置一个碎片群包络，继而在一定边界内，随机给定包络的形状参数A,B,C和φ1,φ2,φ3。

4) 在LVLH坐标系下定义用于描述包络相对航天器初始方位的角度χ∈[0, 2π]和γ∈[-0.5π, 0.5π]，如图4所示，其中，Rini表示包络中心与航天器的初始距离。

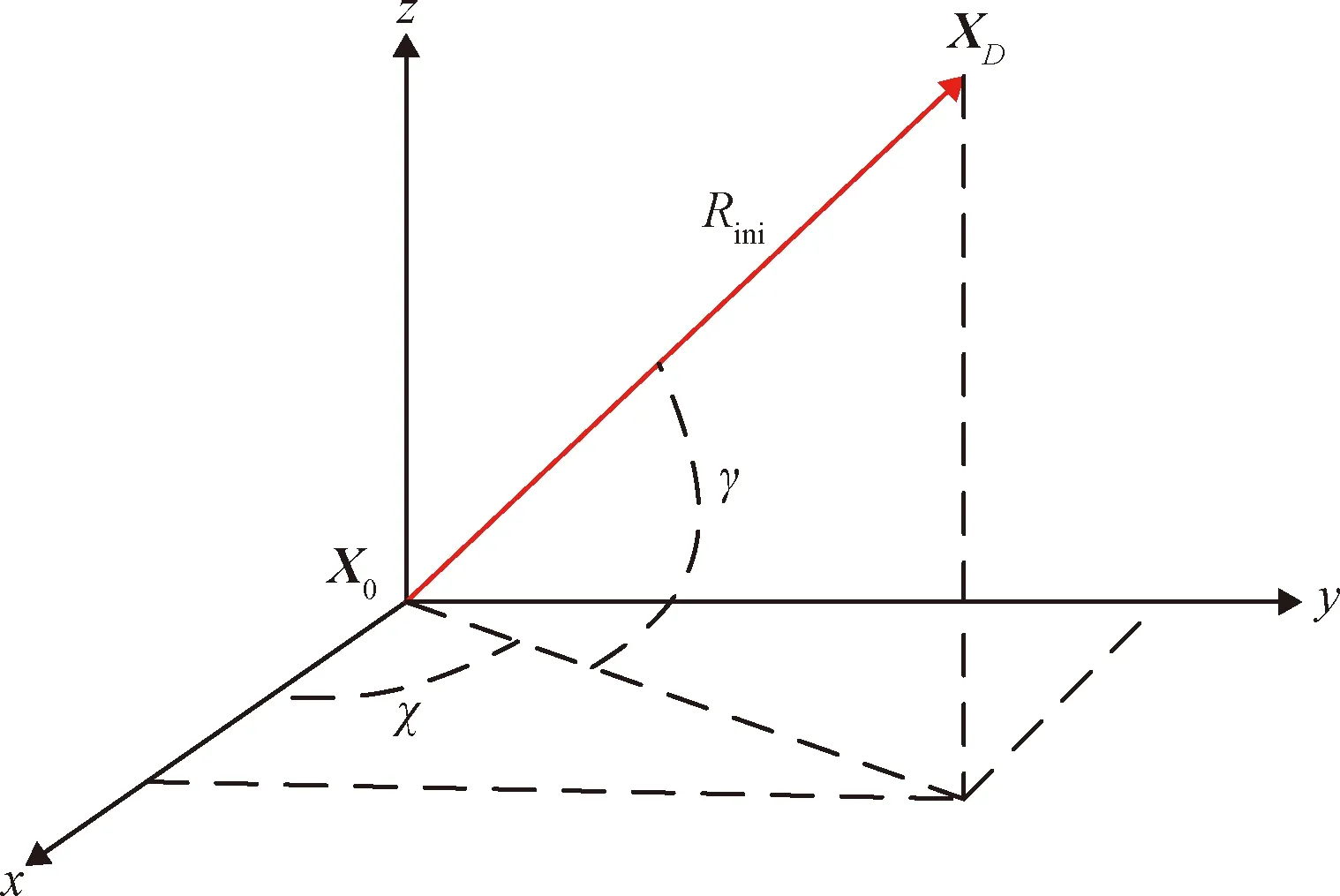
图4 包络初始方位角Fig.4 Initial azimuthal angles of the envelope

5) 设定Rini∈[max(A,B,C)+ΔR,Rmax]，其中，上限为航天器的最大探测距离Rmax，下限为包络尺寸的最长半轴max(A,B,C)与一个确保航天器与包络表面相对距离大于0的距离阈值ΔR之和，则包络中心的初始位置为：

XD=Rini·[cosγcosχ, cosγsinχ, sinγ]T

(23)

6) 设定包络的初始速度Vini：

(24)

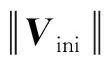
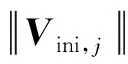
(25)

式中：σV为标准差，Vbase,j为均值，clip表示相应的截断。

然后进入如下循环：

当处于训练回合j时，给定Vbase,j，按上述步骤生成相应的训练场景。经训练后，提取动作网络，在相同Vbase,j的条件下生成F个场景中进行Monte Carlo测试(本文中F=100)：

1)当规避成功率大于等于设定阈值η时(本文中η=90%)，可认为智能体已掌握面向此场景的有效应对策略，则回合数j→j+1，并将均值平移ΔVbase，即：

Vbase, j+1=Vbase, j+ΔVbase

(26)

2)当规避成功率小于设定阈值η时，表示仍需要在此场景下继续训练，则回合数j→j+1，但仍保持原有均值，即：

Vbase, j+1=Vbase, j

(27)

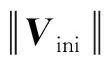
(28)

除了训练场景外，奖励函数r的设计也遵循渐进式学习策略，如式(29)所示：

(29)

4 仿真校验

表1 航天器初始轨道根数Table 1 Spacecraft initial orbital elements

表2 空间碎片群包络参数Table 2 Parameters of envelopes of the space debris clusters

不同时刻(总共1200 s)的航天器机动轨迹如图5所示，各包络Γ(ΔX)的最小值(表征与包络等效表面的最近距离)如图6所示，各轴轨控加速度如图7所示。

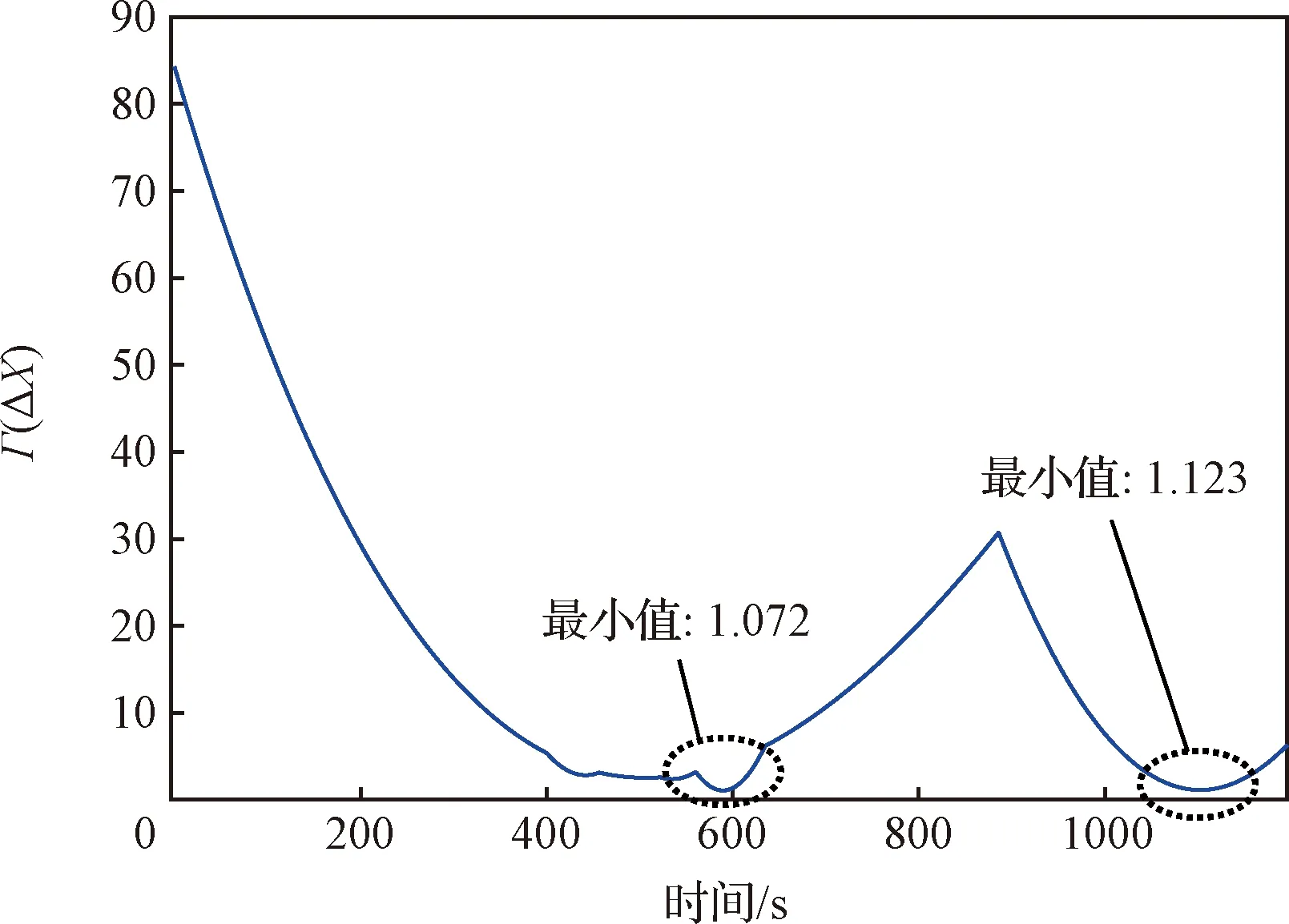
图6 各包络Γ(ΔX)的最小值Fig.6 Minimum values of Γ(ΔX)

图7 各轴轨控加速度Fig.7 Orbit control accelerations in each axis

如图5(a)所示，若航天器不进行规避，则将与包络1发生交会，而基于本文方法实施机动后，航天器能够顺利规避密集分布的碎片群包络1～4，如图5(b)所示。如图5(c)所示，若航天器不对突发包络5做出及时反应，则预期在1093.1 s时双方交会，此时本文方法迅速使航天器做出反应，实现对碎片群包络5的安全规避，如图5(d-e)所示。如图6～7所示，所提方法可使航天器在输入受限的情况下安全规避多发、突发、动态且形状各异的空间碎片群包络，规避机动轨迹相对平滑，有利于控制器跟踪，且根据统计，动作规划算法的单步运行时间在6～8 ms范围内(均值约6.7 ms)，可满足相应的快速反应需求。

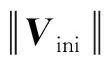
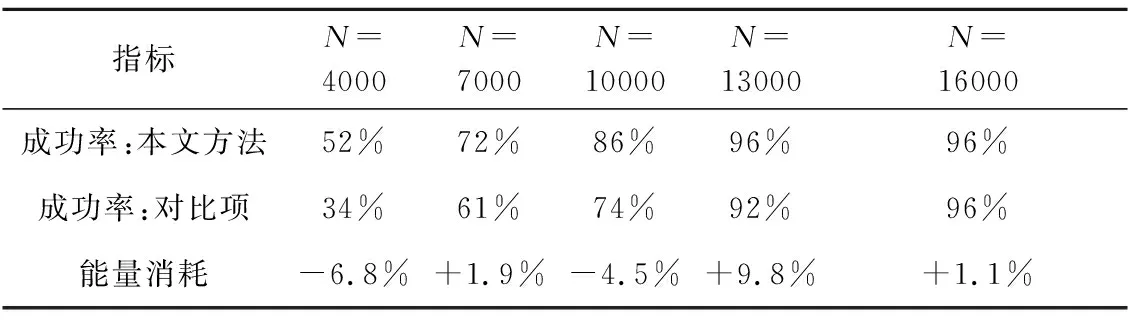
表3 Monte Carlo测试结果Table 3 Monte Carlo test results

图8 训练过程中的奖励函数Fig.8 Reward functions in the training processes

结果可见，经过16000回合充分训练后，二者奖励函数和指标数值基本趋同，且达到了较好的规避效果，表明本文方法和对比项均能使奖励函数进入收敛状态。对比项的奖励函数总体较平滑，但与本文方法相比，当训练回合数较低时(4000、7000和10000回合)，对比项的规避成功率明显偏低，而当回合数较高时(13000回合)，尽管二者规避成功率接近，但对比项整个规避过程的能量消耗要高于所提方法，表明在反应式规划方法中引入本文策略后可以提升训练效率，加快深度强化学习的收敛速度，且能够使反应式规划方法生成质量更高的规划动作，证实了策略对深度强化学习训练的积极作用。所提方法的奖励函数出现了几次急剧下降的过程，原因在于渐进式学习策略的引入使得训练环境发生较大的变化，导致旧环境下训练成型的策略在新环境下短暂地陷入了局部最优。不过经过后续充分训练，智能体很快适应了新的训练环境，从而不断跳出局部最优情况，使奖励函数回升，最终进入收敛状态。此外，尽管测试场景与训练场景存在一定差异，但经过充分训练后的动作网络在测试时仍具有较高的规避成功率，表明网络具有较强的泛化能力。

综上所述，本文所提反应式方法具有规划质量高、计算速度快等优点，能够满足复杂空间碎片环境下的规避任务需求。

5 结 论

针对复杂的空间碎片环境，本文提出一种航天器反应式规避动作规划方法，该方法将IFDS和TD3两种算法相结合，通过TD3在线优化IFDS规划参数，实现对空间碎片群的“状态-动作”最优、快速规避决策。在此基础上，引入优先级经验回放和渐进式学习等策略提升所提方法的训练效率。仿真结果表明，面向多发、突发、动态且形状各异的空间碎片群，所提方法能够快速规划出航天器的安全规避动作指令。