一种基于模型预测的火星返回推力器容错控制再分配方法

杨 博，魏 翔，于 贺，刘超凡

(北京航空航天大学宇航学院，北京 100191)

0 引 言

火星探测器在火星表面采集土壤和岩石样品返回地球，可以用于探究火星的地质特性[1]，为人类实现火星“移民”的目标提供理论依据。由于火星与地球通信延迟大、火星大气环境复杂等因素[2]，火星返回上升器的姿态控制系统需要考虑气动力、液体晃动力等诸多干扰力，同时应该具备自主容错能力[3]。我国天问一号火星探测器的软着陆GNC系统设计有干扰力和干扰力矩的快速识别算法，以及推力器故障快速诊断和重构算法，使探测器具备了在着陆过程中的高容错控制能力，提高了此过程姿态控制的鲁棒性[4]。近年来，随着火星返回任务研究大力开展，使用冗余执行器的过驱动容错控制设计思想，成为当前容错控制技术应用的主要研究方向之一。

对于过驱动系统，控制分配是容错技术应用的典型方法[5-6]。在保持顶层控制律不变的条件下，通过对推力器进行控制指令再分配，实现故障状态下的容错控制[7-8]。常见的控制分配方法有直接分配法、daisy chain法[9]，在此基础上Zhou等[10]提出了两种控制分配方法用于分析在推力器卡死故障下的容错性能；Li等[11]利用基于优化求解的控制分配方法提出了一种推力器卡死故障容错控制方法；Wang等[12]提出基于自适应滑模技术的故障条件下控制指令再分配方法；Galvan-Guerra等[13]提出利用积分滑模控制技术补偿故障产生的干扰的容错控制方法。上述学者所提的方法对于火星上升器推力器的故障均能产生一定的容错控制效果，但都忽略了执行器自身的动态特性对姿态闭环系统造成的影响。Yan等[14]研究表明执行器动态特性能够影响闭环系统的控制性能。董哲等[15]考虑执行器工作特性时仅将响应速度作为优化指标，忽略了执行器动态特性引起的分配误差。Bolling[16]通过对执行器施加过驱动指令力图抵消动态特性的影响，但是这种方法并没有充分利用动态模型的信息，故而造成补偿效果不理想。Hanger等[17]提出的基于模型预测的控制分配方法，在简化意义上解决了考虑执行器动态特性情况下的控制分配问题。

本文基于模型预测的基本控制分配思想，对火星上升器的推力器故障提出一种基于模型预测的推力再分配容错控制新方法，其突出特点是依据推力器各自动态特性，综合考虑分配误差和燃料消耗设计优化指标，建立推力器故障模型作为优化求解器的输出约束，利用模型预测控制分配方法，实现故障状态下的姿态控制系统快速镇定。

1 火星上升器的控制系统推力分配模型

火星返回上升器姿态控制系统模型为仿射非线性模型：

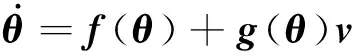
(1)

式中：θ为上升器姿态控制模型中的状态变量；虚拟控制量v为控制力及控制力矩沿上升器本体坐标系的三轴分量。假设上升器带有N个推力器，li=[li,x,li,y,li,z]T,i=1,2,…,N，代表推力器到上升器本体坐标系的位置量，推力器喷管摆动使推力方向变化。设ob,xb,yb,zb为上升器本体坐标系，oi,xi,yi,zi为推力器坐标系，其关系如图1所示。

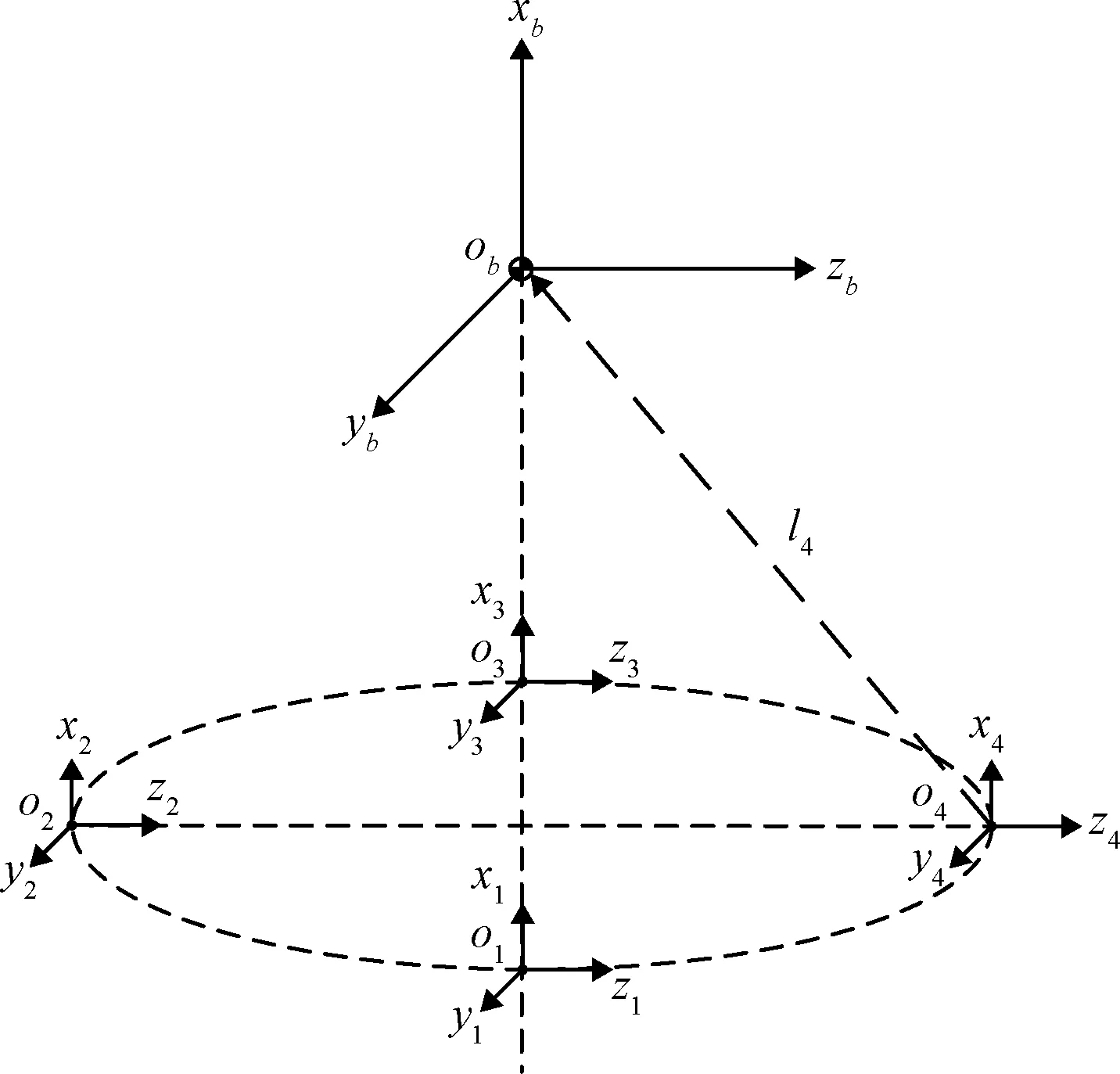
图1 推力器几何位置示意图Fig.1 Geometric position of the thruster

推力器i的推力Ti(t)映射到上升器本体坐标系中的力Tb,i(t)和力矩Mb,i(t)表示为：

(2)

(3)

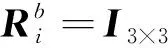
(4)

记N个推力器推力T为

(5)

根据式(3)，N个推力器产生的总的力和力矩为

(6)

(7)

映射矩阵G为

(8)

映射矩阵H为

(9)

根据效率矩阵K的定义,有

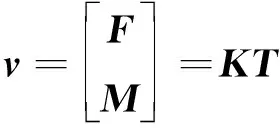
(10)

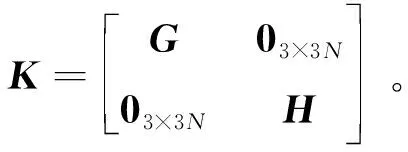
1.1 推力器线性二阶环节

将火星上升器的推力器动态模型建模为线性二阶环节，如下：

(11)

式中：xi,a表示第i个执行器的动态模型的状态变量；ui为控制输入；yi表示第i个推力器的推力沿推力器坐标系的三轴分量。假设各个执行器的动态特性相互独立，对N个推力器则有

(12)

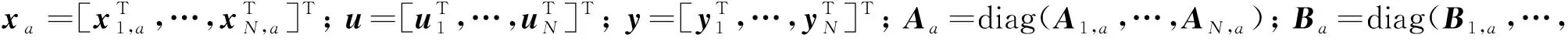
1.2 推力器模型修正

若火星上升器推力器的动态模型存在建模参数误差，则对式(12)进行如下修正

(13)

假设误差项ΔAa和ΔBa可以由一组特定的未知参数表示，如下所示

ΔAaxa+ΔBau=d(xa,u)ϑ

(14)

假设：推力器负载动态模型的状态量xa以及映射矩阵d(xa,u)具体表达式已知。

将式(14)代入式(13)中可以得到

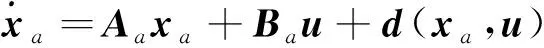
(15)

用自适应估计算法对式(15)模型参数进行估计。定义如下的状态估计方程：

(16)

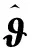
(17)

(18)

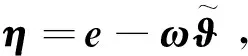
(19)

根据如下的动态方程定义矩阵Qe∈p×p和Ce∈p:

(20)

(21)

假设存在时间点tc使得Qe(tc)是可逆的，那么对于∀t≥tc有

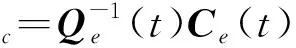
(22)

式中：ϑc为不确定参数ϑ的估计输出。根据式(20)有

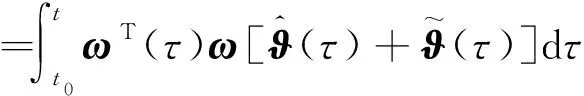
(23)

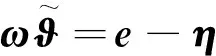
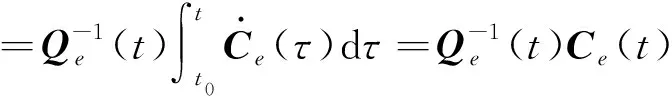
(24)

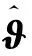
(25)

(26)

假设(Ak,Bk)是可控的，(Ak,C)是可观的。控制分配任务即求解输入uk-1使得Kyk与虚拟控制量vk相等。

2 火星上升器推力控制分配

控制分配任务的总体框图如图2所示：

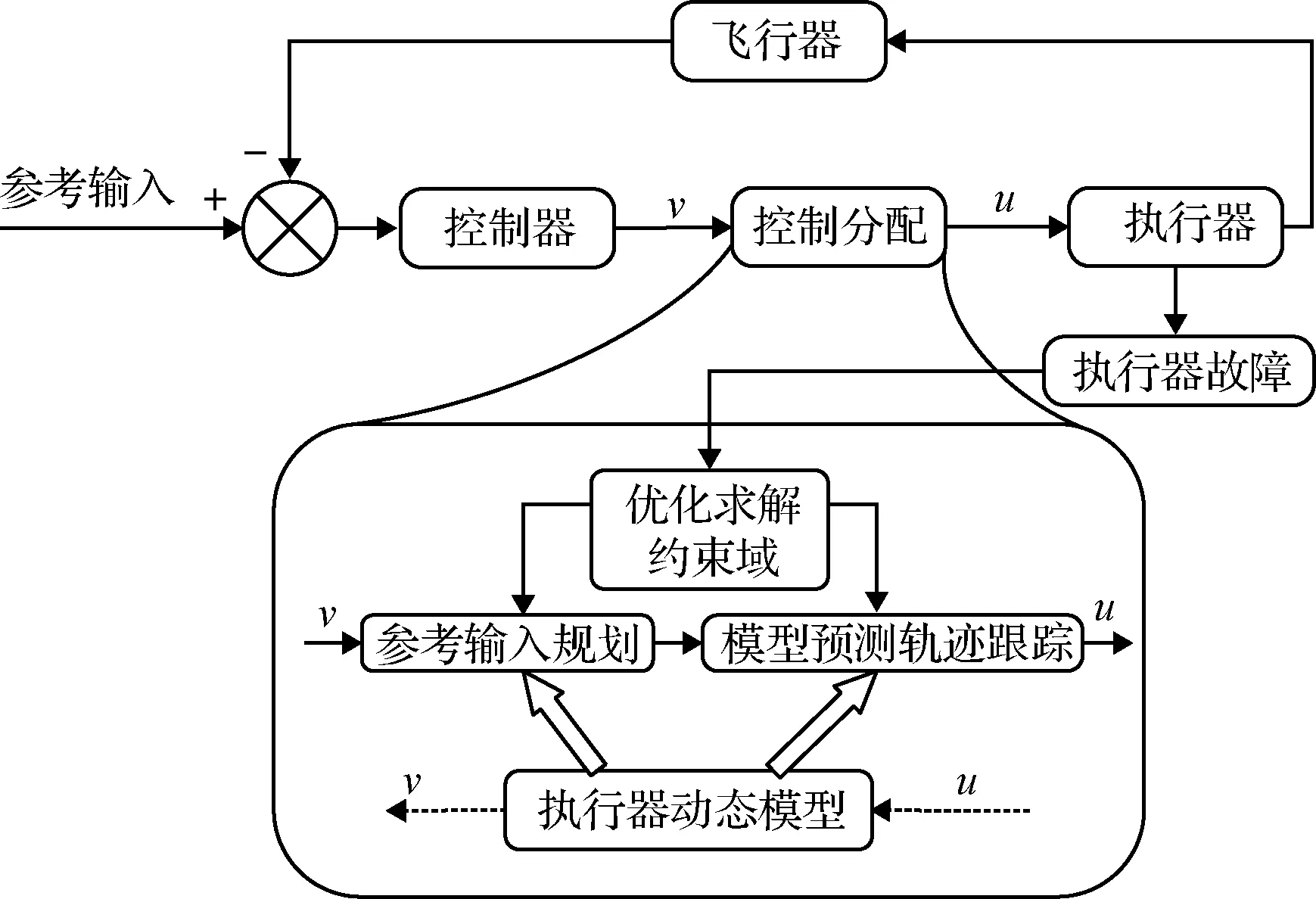
图2 动态控制分配总体方案图Fig.2 Scheme diagram of the dynamic control allocation

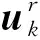
2.1 基于优化求解的参考控制输入规划

由式(26)得到

(27)

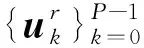
(28)

式中：

(29)

写为优化问题，定义

(30)

(31)

式中：ω1,ω2,ω3为调节参数；ω1为控制量的模，表示燃料消耗最小；ω2表示分配误差最小；ω3表示松弛因子最小。则约束条件为:

(32)

式中：Ωy表示输出约束。

2.2 基于模型预测的控制分配

令性能指标函数为：

(33)

式中：Q>0,R>0,Ψ>0,xk+i|k是在时刻k时的预测状态量,xk|k=xk。

定义跟踪误差为：

(34)

将式(33)写为:

(35)

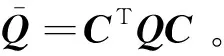
由式(26)和式(34)，i=0,1,…,P-1，得到如下的约束方程:

(36)

系统参数Ak和Bk为自适应估计方法得到的当前时刻的估计值，则最优控制为:

(37)

3 推力器容错控制再分配设计

以推力器卡死故障为例，故障约束可以表示为推力沿三轴分量的线性约束，即存在矩阵M使得

Myk=0

(38)

说明：假设共有四台推力器，推力器1卡死时，输出推力T1存在如下所示的约束:

(39)

式中：T1x,T1y,T1z分别为T1沿推力器坐标系的三轴分力;α*,β*,γ*分别为T1与推力器坐标系三轴的夹角。记约束矩阵为

(40)

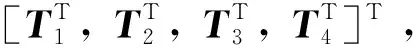
在预测时刻i, 1≤i≤P，推力器预测输出yk+i|k的表达式为：

(41)

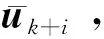
(42)

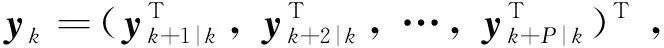
Skz+Tk=yk

(43)

式中：

(44)

(45)

若卡死故障发生，则将式(38)代入式(43)作为新增约束：

M(Skz+Tk)=0

(46)

模型预测跟踪控制求解过程中，对于输出yk+i|k的速率约束可以通过相邻控制周期的时间间隔Ts转换为位置约束，速率约束如下，0≤i≤P:

(47)

由式(47)和式(43)整理得到：

(48)

式中：

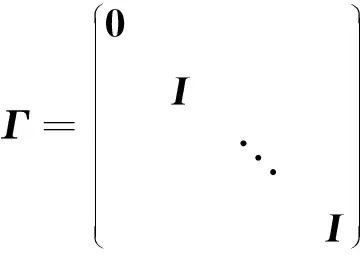
(49)

根据式(48)可以得到关于优化变量z的线性约束:

(50)

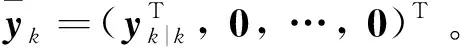
4 仿真校验

4.1 上升器姿态动力学模型

假设上升器在射面内运动，带液体晃动[19-20]，则火星上升器姿态动力学方程如下所示，沿xb轴方向:

T-FX

(51)

沿zb轴方向:

F-FZ

(52)

绕yb轴转动:

mfgasin(θ+φ)=M+(F-FZ)b-MY

(53)

液体晃动等效单摆动力学方程:

(54)

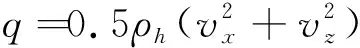
火星大气密度随海拔高度变化可以建模为一维指数模型

ρh=ρ0e-(h-h0)/hs

(55)

假定姿态动力学方程(51)中推力T较大且为恒定常值，并且不考虑液体燃料的消耗，在上升器机动时，姿态角变化较小，晃动为微幅晃动，则液体晃动和气动力对xb轴方向的加速度影响较小，因此可以用下面的近似方程代替

(56)

定义控制指令(u1,u2)如下所示

(57)

式中：

(58)

mgbsinθ-MY

(59)

(60)

则可以得到简化的姿态动力学方程

(61)

式中：

(62)

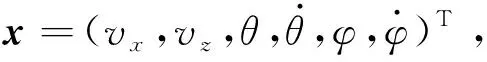
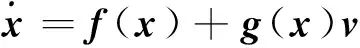
(63)

式中：

(64)

利用反馈线性化设计状态反馈控制器[21]：令S=[05×1,I5×5]，定义映射如下所示，

H0(x)=Sx

(65)

使用李导数记号，有下列表达式：

(66)

反馈输入项为

(67)

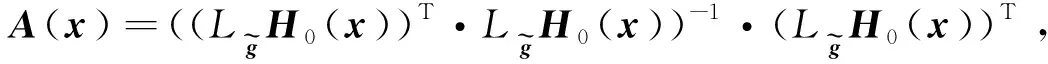
v=u*+A(x)FS0x

(68)

其中反馈矩阵F为常值矩阵。

4.2 仿真条件

(1)仿真实验中，推力器数目N=4，推力器动态模型为:

(69)

式中：自然频率ω=40 rad/s；阻尼η=0.05。模型参数误差不确定项映射矩阵d(xa,u)记为d:

(70)

不确定参数ϑ维度p为1,真实值为2。

(2)上升器系统参数：m=600 kg,I=720 kg·m-2,mf=100 kg,a=0.32 m,b=0.25 m,T=3500 N,ε=0.19 kg·m2·s-1,If=90 kg·m-2；火星大气参数：ρ0=2×10-4kg·m-3,h0=40000 m,hs=7500 m,h=5000 m；气动参数：Cz=0.04,xd=0.75 m,xz=0.62 m,Sm=0.23 m2；控制器反馈矩阵取值为：

(71)

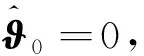
l=[l1,l2,l3,l4]=

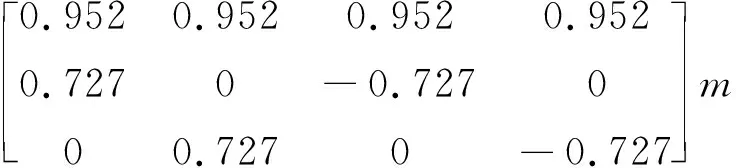
(72)

四个推力器模型输出约束为：

(73)

式中：推力最大值Tmax=2000 N，摆角最大值αmax=10°；推力变化速率最大为150 N/s。

4.3 仿真验证及结果分析

4.3.1推力器为二阶模型的控制分配

假定推力器为线性二阶环节，见1.1节，得到如下仿真结果。

图3所示为姿态角θ和液体晃动等效摆角φ的变化规律，相应的角速度如图4所示。

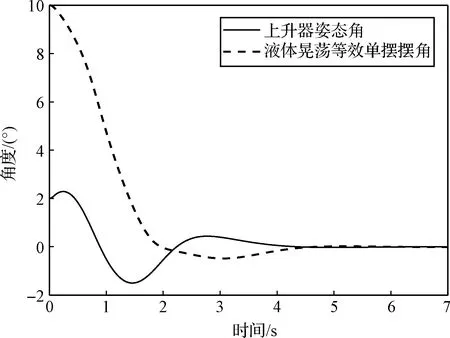
图3 上升器姿态角和等效单摆摆角Fig.3 Attitude angle and equivalent single pendulum deflection angle of the ascent vehicle

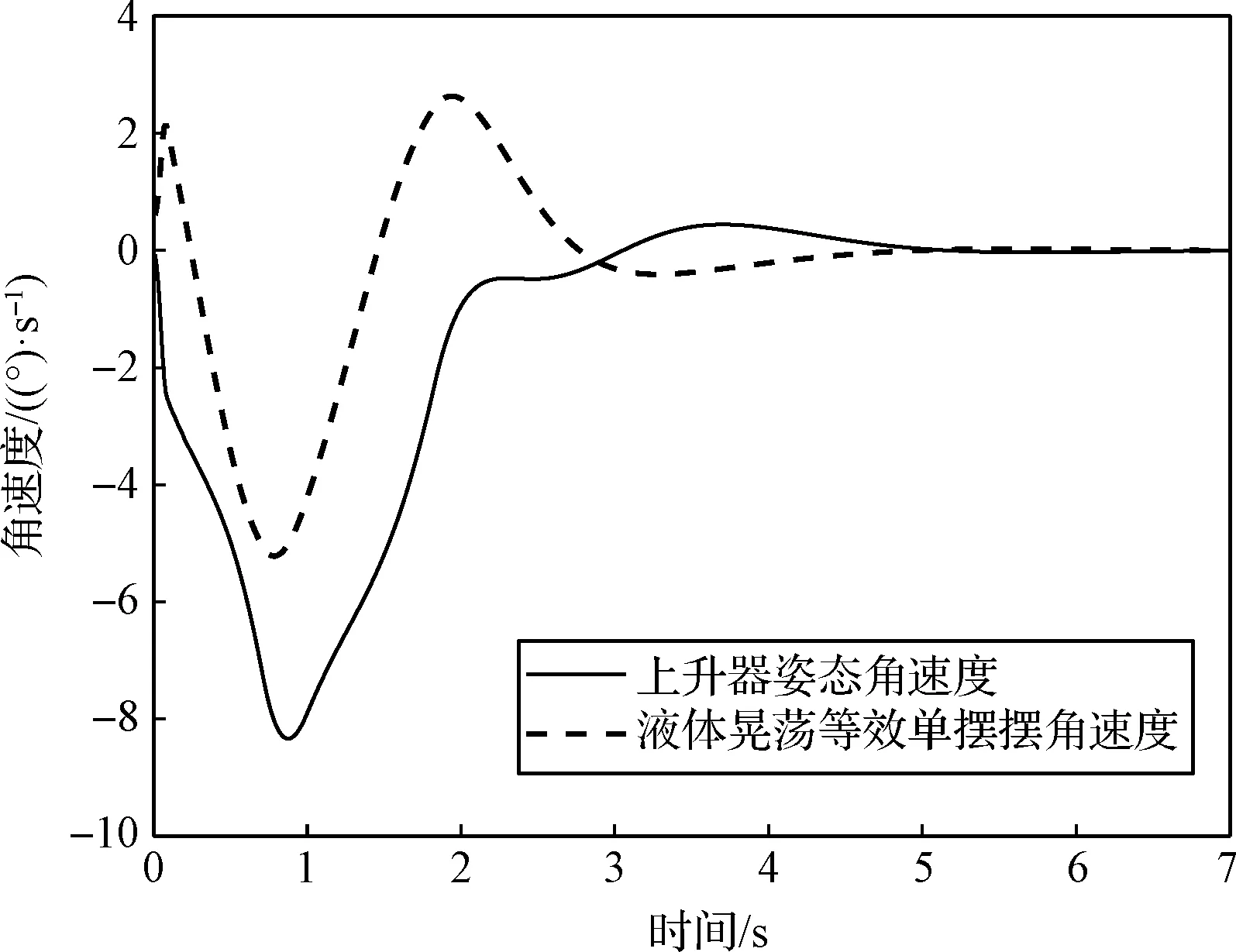
图4 上升器姿态角速度和等效单摆摆角速度Fig.4 Attitude angular velocity and equivalent single pendulum deflection angle velocity of the ascent vehicle

从图3和图4可以看出，上升器的姿态角和液体晃动的等效摆角在5 s后均趋于零，说明若推力器为二阶系统模型时，实施推力控制分配，可以快速抑制由液体燃料晃动造成的姿态角误差，提高了系统可控性。

四台推力器的推力如图5所示，摆角如图6所示，描述了各推力器在参与推力动态控制分配过程中的变化规律。

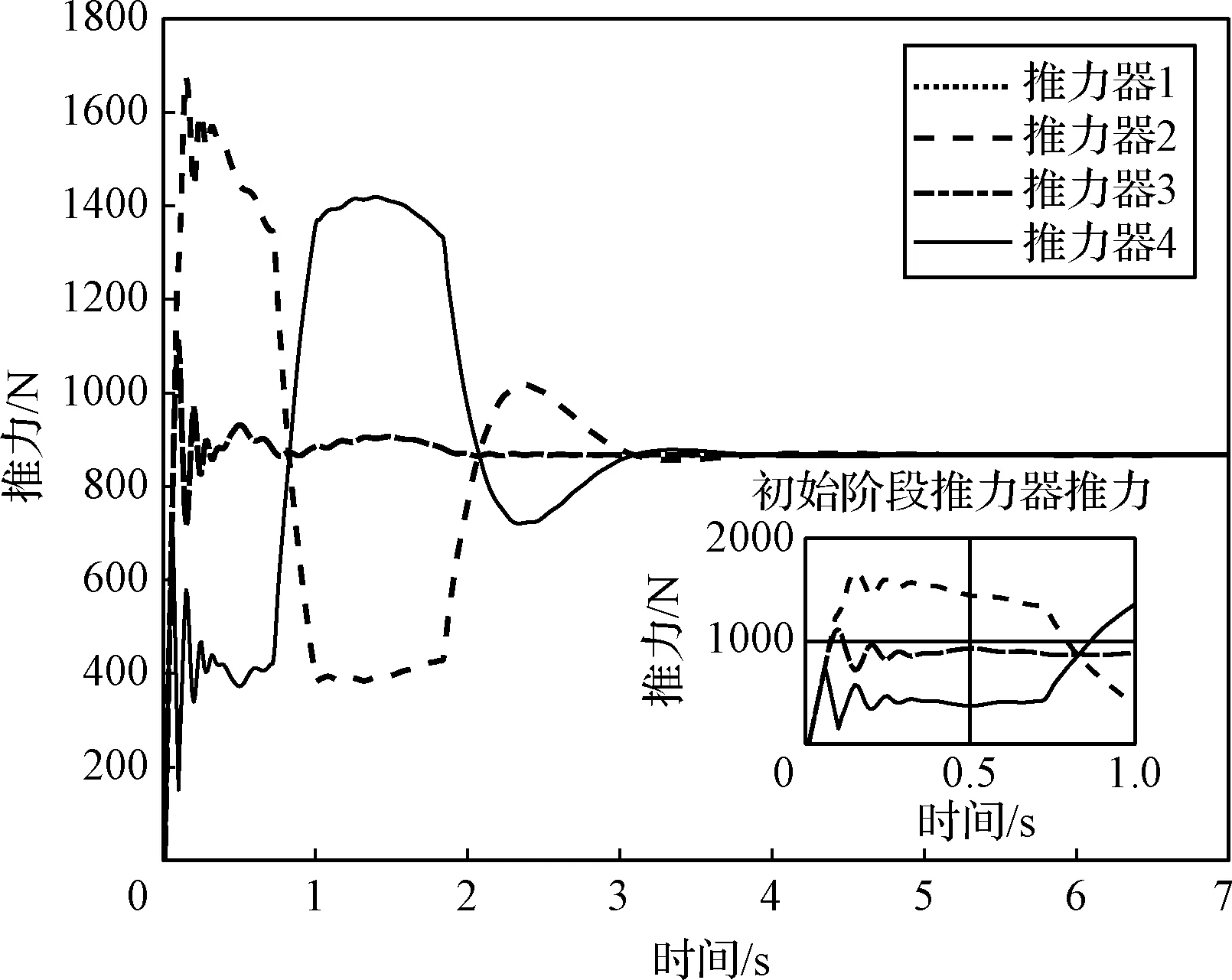
图5 四台推力器推力Fig.5 Thrust of the four engines

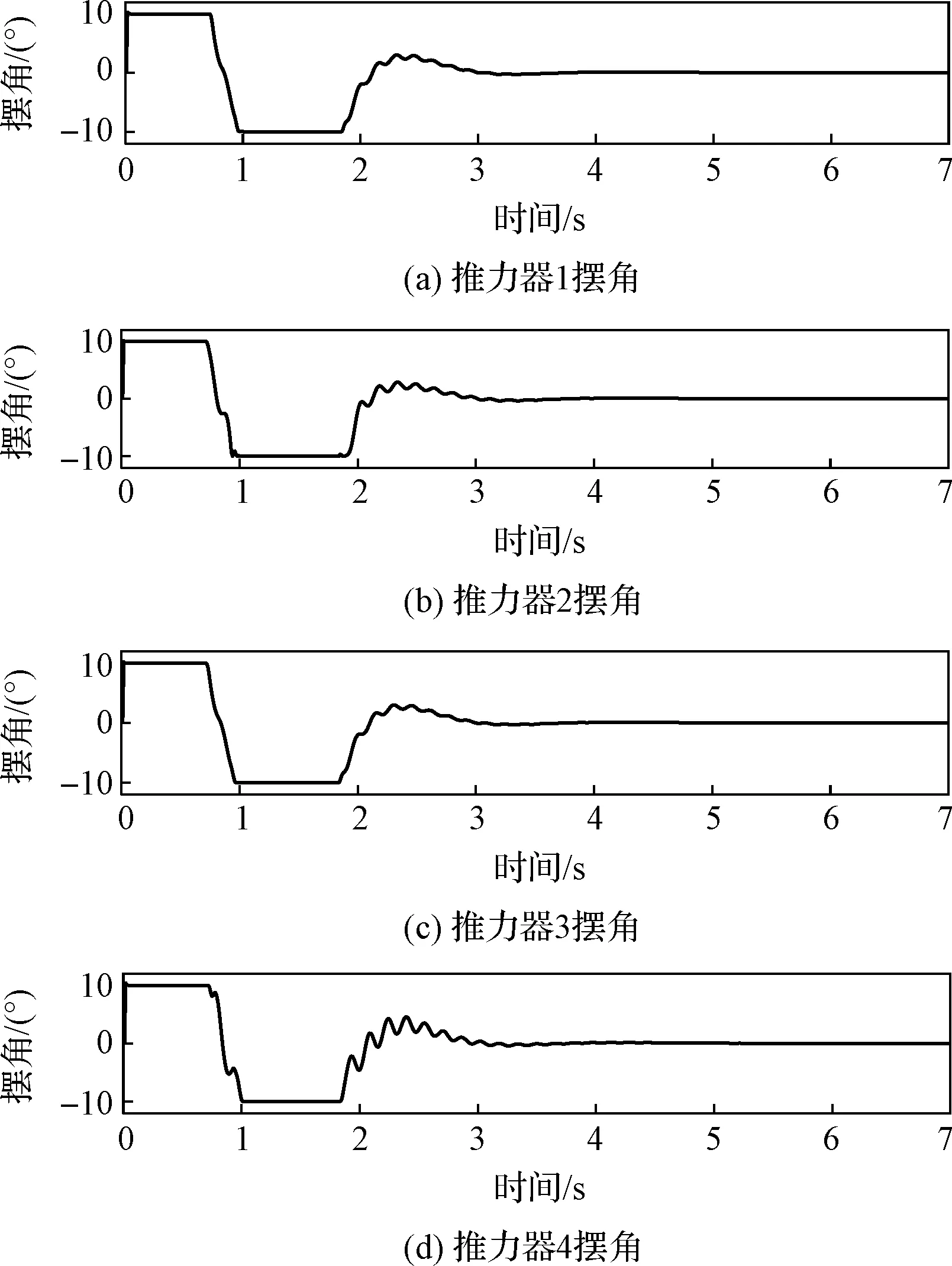
图6 四台推力器摆角Fig.6 Swing angle of the four engines

各推力器推力最大值限制在2000 N以下，输出推力趋于875 N，图6中推力器摆角最大值为10°，满足预先假定的推力限制条件，结果说明，四台推力器不但可以将上升器控制在弹面内，同时还可以沿xb轴方向使上升器上升获得所需求的3500 N额定推力。

对比未使用1.2节模型预测跟踪控制方法的推力变化曲线如图7所示，明显看出初始阶段推力变化幅度大，而且实施时间长，倘若出现更大的随机扰动，将很难保证推力分配使系统快速稳定，甚至可能导致上升失败。

图7 未使用模型预测跟踪控制时的推力Fig.7 Thrust without model predictive tracking control

使用伪逆法和加权伪逆法[22]结合线性状态反馈跟踪控制作为仿真对比，得到如下所示的实际控制力和控制力矩的结果:

根据图8和图9可以得出，本文提出的基于模型预测的控制分配方法能够有效避免由于推力约束引起的控制量抖动，相对于伪逆法、加权伪逆法输出的实际控制力和力矩更加平稳，这是因为优化求解的过程中不仅满足推力大小和方向约束，同时考虑了预测时间域内的分配误差和燃料消耗指标。

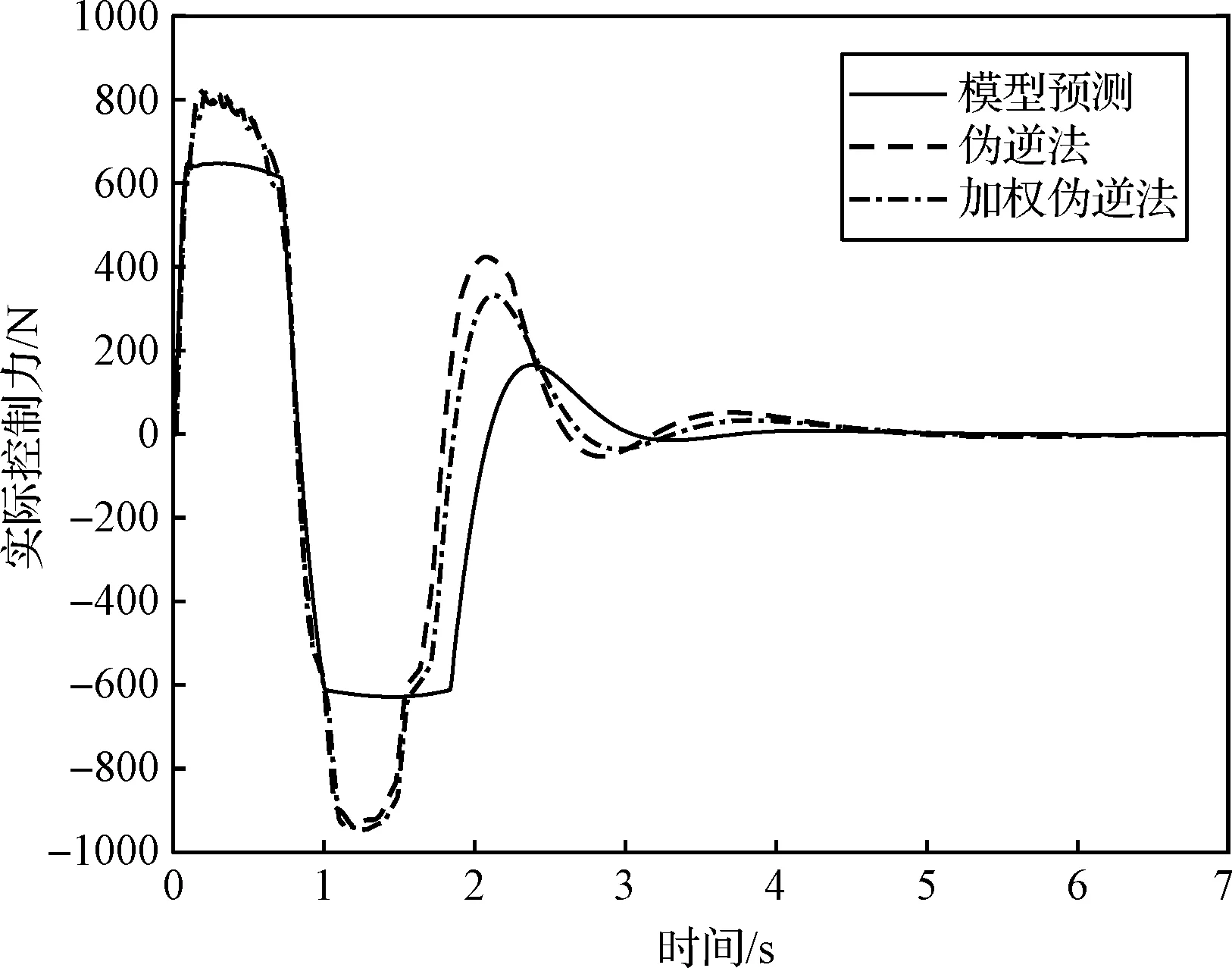
图8 三种控制分配方法下的实际控制力Fig.8 Actual control force under the three control methods

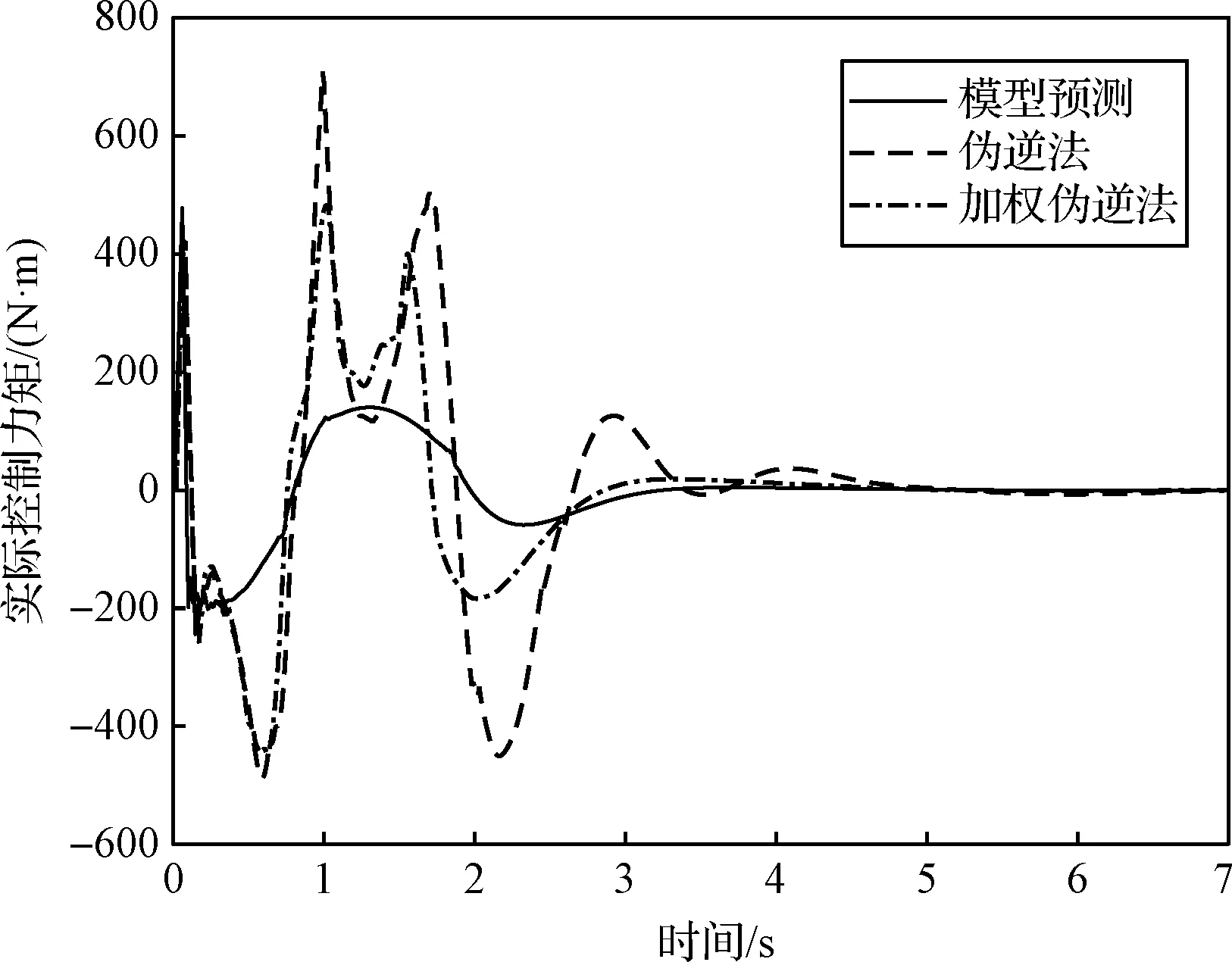
图9 三种控制分配方法下的实际控制力矩Fig.9 Actual control torque under the three control methods

4.3.2推力自适应动态控制分配

根据1.2节做推力器模型修正，即对二阶模型作参数估计，用2.1节的自适应动态分配方法得到如下结果:

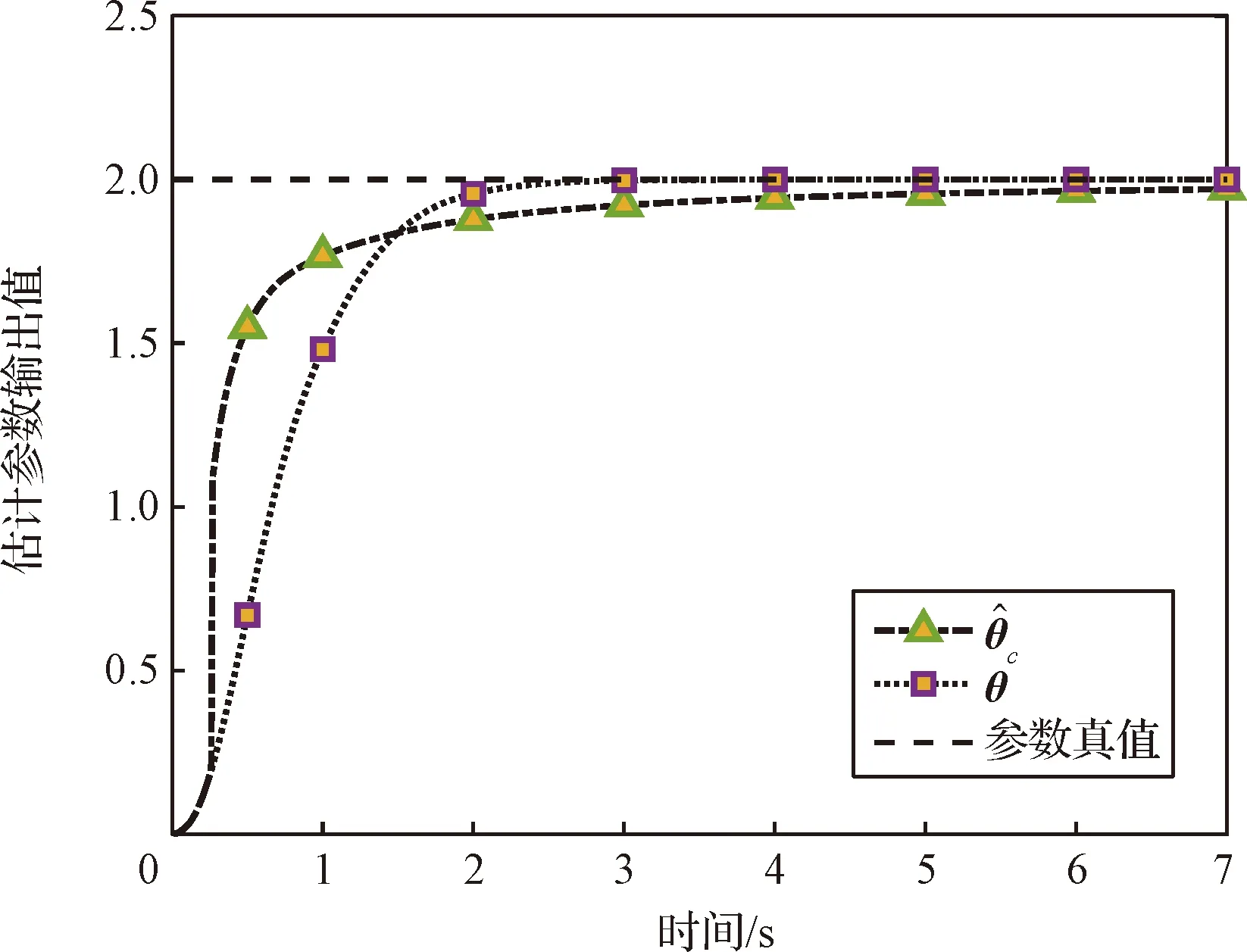
图10 推力器动态模型参数估计Fig.10 Parameter estimation of the thrusters’ dynamic model

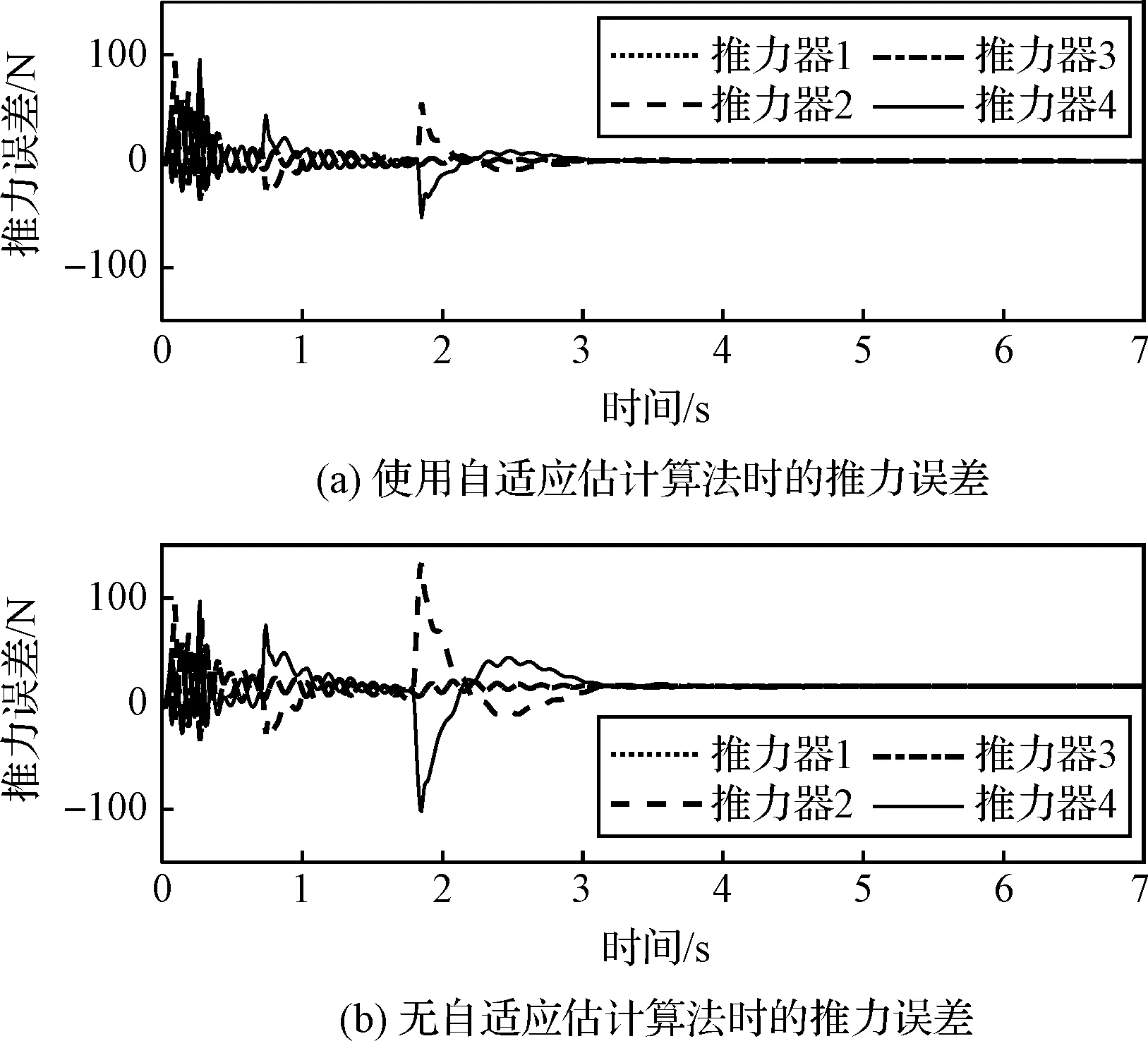
图11 使用和未使用自适应分配算法的推力偏差对比Fig.11 Comparison of thrust deviations with and without the adaptive allocation algorithm

由图11可以得出，在1～2 s期间，未使用动态自适应分配算法时推力发生明显偏差，约130 N，这是由于此时推力指令变化幅度较大，如1.8 s时4号推力器的推力从1300 N下降到800 N以下。

而在使用动态自适应分配方法后，推力与基准值的偏差最大不到50 N，可以认为，使用模型参数估计可以对推力指令实施有效跟踪控制，可以有平滑输出减少超调，在一定范围使推力偏差减小60%以上。

4.3.3推力器容错控制再分配

假定推力器发生卡死故障，对推力器卡死故障实施容错控制再分配。

在1.95 s时，令1号推力器摆角卡死在-6°，此时式(38)中的约束矩阵为：

(74)

在2.45 s时，使用容错控制再分配方法对推力进行再分配，仿真结果如图12所示。

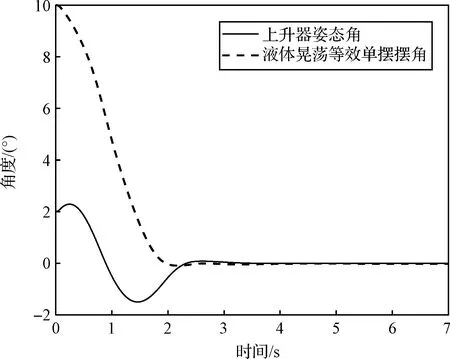
图12 上升器姿态角和等效单摆偏转角Fig.12 Attitude angle and equivalent single pendulum deflection angle of the ascent vehicle

可以看出，收敛时间、稳定误差、超调等各项指标均较优越。

图13和图14所示为四台推力器在容错控制过程中各自的推力和偏角的变化过程，可以看出，本文提出的推力器容错控制再分配方法对解决火星上升器推力器卡死故障是非常有效的。

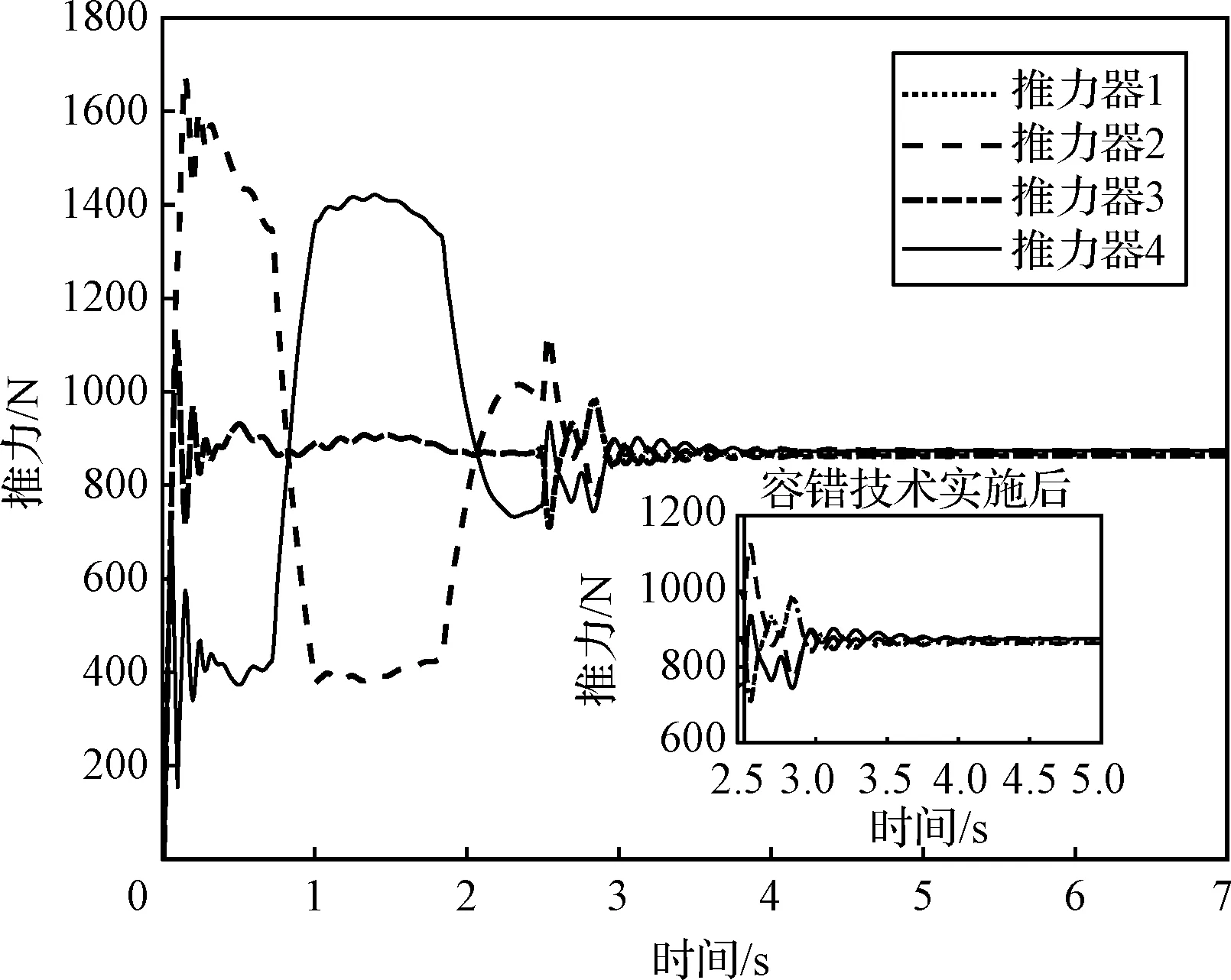
图13 四台推力器推力Fig.13 Thrust of the four engines

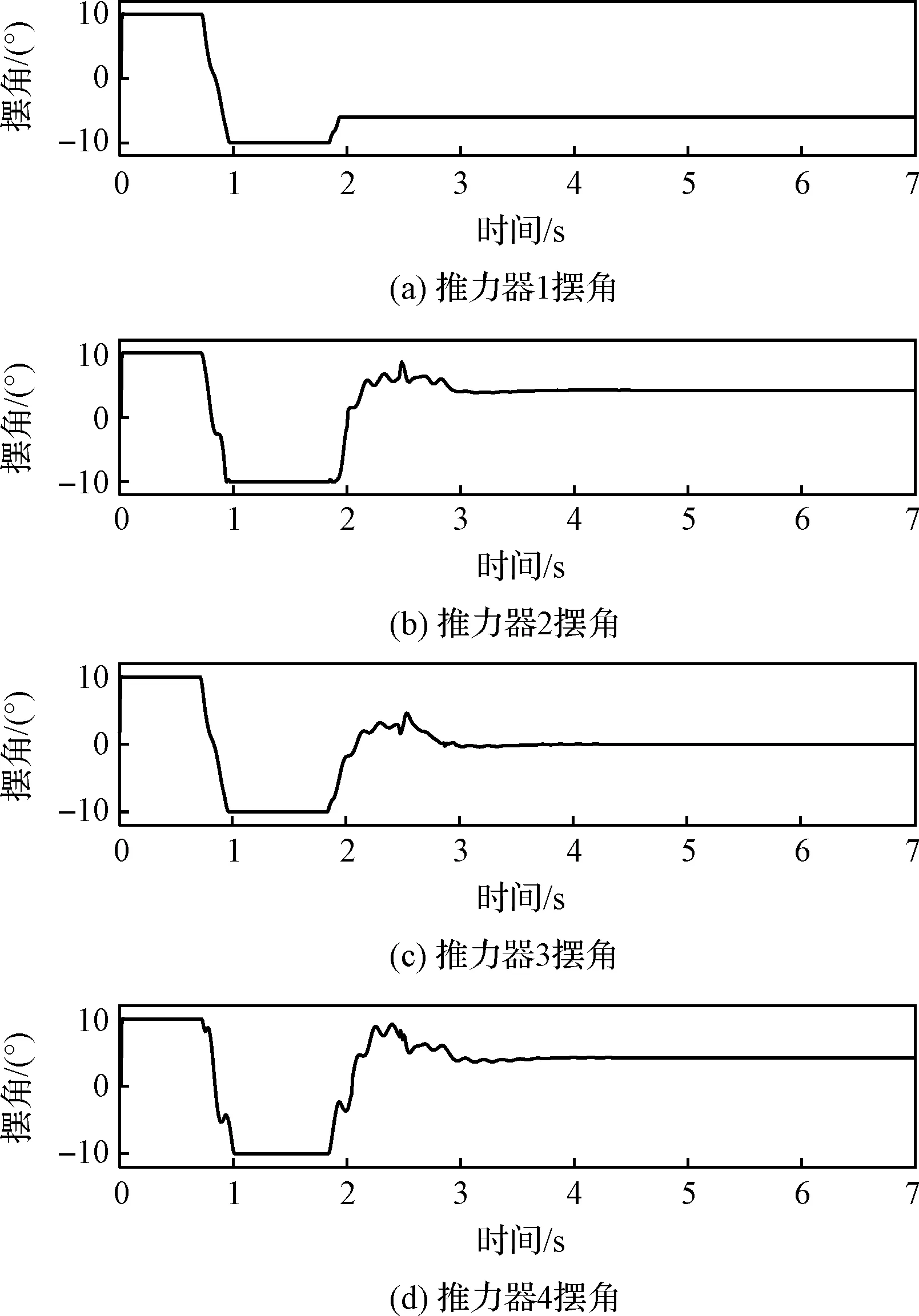
图14 四台推力器摆角Fig.14 Swing angle of the four engines

5 结 论

本文针对火星返回上升器的推力器故障容错技术研究，提出基于模型预测的容错控制再分配方法，结论如下：根据火星返回器的推力器动态特性获得基础模型，并采用参数估计方法实时修正逼近真实模型，使推力器输出误差能够减小60%以上；使用推力再分配技术，实现推力器容错控制再分配，3～5 s即可实现对控制指令的稳定跟踪，姿态控制系统快速镇定；用推力器故障状态下的输出约束调整优化求解器的约束域，实现最小化分配误差和最小燃料消耗意义下的最优控制再分配。