一种基于学习的高超声速飞行器智能控制方法

王 冠，夏红伟

(哈尔滨工业大学航天学院，哈尔滨 150001)

0 引 言

吸气式高超声速飞行器采用超燃冲压发动机，具可重复使用、飞行能力强的特点,其动力学控制作为高超声速飞行器研制中的关键问题之一，在近年得到了广泛关注[1]。

随着控制理论的发展，传统比例-积分-导数(PID)控制[2]、滑模控制[3]、容错控制[4]等控制方法在高超声速飞行器控制领域的研究已经取得了一定成果。为了解决存在未知动态且无法精确建模的高超声速飞行器控制问题，一些学者采用自适应和神经网络技术，提出了新颖的控制方法。文献[5]针对带攻角约束的高超声速飞行器控制问题，提出一种基于非对称时变障碍函数的自适应控制方法，在保证良好跟踪性能的同时能够满足攻角约束限制。文献[6]利用神经网络技术逼近未知非仿射动态，结合漏斗控制与低通滤波器，提出一种不需要虚拟控制律的控制策略，确保了跟踪误差的瞬态性能和稳态性能，但其设计相对复杂且参数较多。自适应控制和神经网络控制在处理模型参数不确定性方面具有先天优势，但学习能力较有限，通常需要引入大量的参数更新律，强烈依赖于神经网络的更新规律，极大地增加了控制算法的结构复杂度和控制参数整定难度[4-9]。如何处理控制效果与算法复杂度之间的矛盾，是当下高超声速飞行器控制领域亟待解决的关键问题之一。与传统控制方法相比，确定学习能够从动力学系统的神经网络控制过程中实现未知动态的学习[10]。在对未知动态的知识获取、存储以及利用方面具有明显优势，越来越多研究工作将确定学习的思想应用于解决工程实际问题[11-12]。例如，文献[13]利用确定学习理论对机械手系统的未知动态进行知识获取，提出一种预设性能神经学习控制器，实现了机械手在预设性能约束下的跟踪控制。高超声速飞行器动力学模型的强非线性、强不确定性、飞行工况的复杂性，以及现有算力、可靠性等因素都制约着自适应和神经网络控制在实际工程中的落地应用，考虑到上述问题，将确定学习思想引入高超声速飞行器的控制设计中，在减轻线上控制计算负担方面具有极大潜力。此外，实际工程还要求考虑超燃冲压发动机的可执行范围存在一定限度，即燃油阀开度的上限和下限约束，保障高超声速飞行器的稳定飞行控制。因此，在实际工程中必须考虑燃油阀开度受限下的控制问题。文献[14]通过构造自适应辅助系统提出一种基于上界估计的自适应飞行控制策略，在保证预设跟踪性能的同时克服了燃油阀开度受限的问题。目前，常见的处理手段包括构造辅助系统[14]、构造辅助线性矩阵不等式[15]等，能够有效处理输入受限问题，但是以上方法对模型依赖性强、参数调节相对复杂。

需要指出的是，上述控制策略通常采用时间触发的方式，为了保证系统的稳定性并达到预期性能，控制量的更新周期一般相对较小。这种机制可能造成不必要的通信和计算资源消耗，更严重的情况是加速高超声速飞行器元器件的老化和系统能源的损耗。为了解决基于时间触发控制带来的资源浪费，近年来学者们基于事件触发机制做了大量工作[16-17]。文献[18]针对无人机系统提出的事件触发控制方案与传统的时间触发采样方案相比，能够显着降低网络利用率，同时获得令人满意的控制性能。尽管在现有文献中事件触发控制研究已经得到了一定发展，但在高超声速飞行器控制领域中仍有待研究，该类控制问题逐渐引起学界的关注。

基于上述分析，本文针对高超声速飞行器控制问题，提出一种基于学习的智能控制方法。针对输入受限的速度子系统，提出一种基于近端策略优化算法(Proximal policy optimization, PPO)的智能权值分配控制方案。考虑通信资源有限的高度子系统，提出一种基于事件触发的确定学习控制方案。该方案包含离线学习训练和在线触发控制两个阶段。该控制方案设计分为两个步骤：离线学习训练阶段和在线触发控制阶段。第一步，首先在具有充足通信资源的离线控制测试端，利用径向基函数(Radial basis function, RBF)神经网络设计控制器，获取高超声速飞行器系统的未知动态知识。第二步，对于高超声速飞行器的远程在线控制阶段，结合存储的经验知识构建在线触发控制器。随后，结合高超声速飞行器动力学模型与李雅普诺夫理论验证了所提出的控制方案能够保证跟踪性能和闭环系统的稳定性。

本文的主要贡献总结如下：1)利用强化学习来解决输入受限下的速度跟踪控制问题，将经过离线学习训练获得的智能体应用于在线控制，降低了速度子系统控制器的计算量；2)利用确定学习思想来解决高超声速飞行器的高度跟踪控制问题，在本地系统资源充足的情况下，经过离线学习训练获取系统的未知动态知识，利用经验知识进行在线控制阶段方案设计，降低了由神经网络权值的在线频繁更新带来的计算负担；3)与已有的神经自适应控制方案[9]不同，所提出的方案在保证在线暂态跟踪性能的同时，通过结合事件触发机制实现了更少的触发次数，避免不必要的通信资源浪费。

1 系统描述和预备知识

1.1 高超声速飞行器的纵向模型

本文采用高超声速飞行器纵向动力学模型[19]

(1)

该模型包含5个状态量X=[V,h,γ,α,Q]T，V，h，γ，α和Q分别表示飞行器的速度、高度、航迹角、攻角和俯仰角速度；m和g分别表示飞行器的质量和重力加速度，Iyy表示转动惯量；T，D和L分别表示发动机推力、阻力和升力，Myy表示俯仰力矩，具体表达式为

(2)

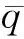
1.2 预备知识

为了实现离线学习控制的知识获取以及存储，给出几个必要的引理。

引理 1[10].对于紧集上的未知平滑非线性函数fi(xi)，可利用RBF神经网络对其进行逼近：

(3)

(4)

(5)

式中：εi为任意小的逼近误差，且常值神经网络权值可通过如下方式计算

(6)

式中：tb>ta>T,[ta,tb]为系统稳态后的时间段。

1.3 控制目标

对于输入受限的速度子系统，设计基于强化学习的智能控制方案，使得输出速度V稳定跟踪参考信号Vr。对于通信资源有限的高度子系统，设计基于事件触发的确定学习控制方案，使得输出高度h稳定跟踪参考信号hr。

2 控制器设计

本节首先针对速度子系统进行强化学习训练设计，实现速度参考信号的跟踪；然后通过设计高度子系统跟踪控制器，使得高度紧密地跟踪参考轨迹；在此基础上进行离线神经网络训练，获取并存储神经网络权值；最后结合获取的经验知识，构造在线触发控制器。图1为本文所提出的智能控制方案示意图。

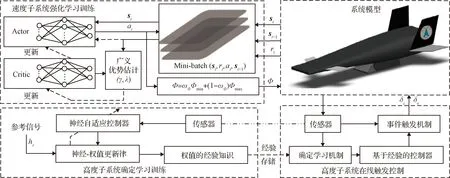
图1 基于学习的高超声速飞行器智能控制方法示意图Fig.1 Schematic diagram of learning-based intelligent controller design for hypersonic flight vehicle

2.1 速度子系统

定义Vr为速度参考信号，则速度跟踪误差为eV=V-Vr，其导数可表示为

(7)

在速度子系统中，考虑实际系统中燃油阀开度饱和的要求，将控制指令输入表示成如下形式：

(8)

式中：Φc表示理想的燃油阀开度指令；Φmin表示燃油阀开度的下界，源于热管理系统中主动冷却功能的需求；Φmax表示燃油阀开度的上界，为了避免发生热阻现象而危害系统的稳定性。

基于上述分析，可将式(8)改写成基于权值分配的形式：

Φ=ωΦΦmin+(1-ωΦ)Φmax

(9)

式中：ωΦ∈[0,1]是一个表示权重的正常数。

为了实现燃油阀开度指令的快速响应以及抗饱和需求，本文提出了基于PPO算法的智能权值分配控制器。PPO算法是一种Actor-Critic方法[21]，结合广义优势估计方法，可将其优势函数表示为：

(10)

设置目标函数为

(11)

式中：πθ是以θ为参数的随机策略网络。

本文对于速度子系统的智能控制设计中，将PPO算法中的旧策略πθold与高超声速飞行器模型进行多次交互，产生用于强化学习训练的数据。

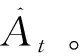
(12)

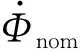
注1.与文献[22]中所采用的智能PID参数整定相比，本文所提出的基于PPO算法的智能权值分配控制器考虑了控制输入的幅值约束，在奖励函数设计中兼顾了工程实际意义。

2.2 高度子系统

在具有充足通信资源的离线控制测试端，首先通过利用高斯RBF神经网络设计神经自适应控制器，获取高超声速飞行器动力学系统的动态知识。

2.2.1(h-γ)子系统

定义高度误差变量为eh=h-hr，并考虑到sinγ≈γ，对其求导得

(13)

式中：gh=V。

设计如下的航迹角虚拟控制律

(14)

然后定义航迹角误差变量为eγ=γ-γd，结合式(1)对其求导得

(15)

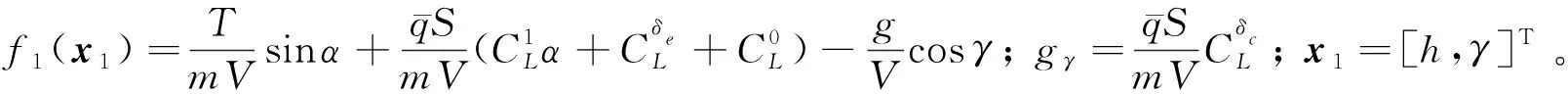
设计鸭翼控制律为

(16)

其更新律设计如下

(17)

2.2.2(α-Q)子系统

定义期望攻角α*，设计攻角虚拟控制律：

αd=α*-eγ

(18)

定义攻角跟踪误差eα=α-αd，结合上式可将eα的导数表示为

(19)

对此，设计俯仰角速度的虚拟控制律：

(20)

定义俯仰角速度跟踪误差为eQ=Q-Qd，则其导数可写为

(21)

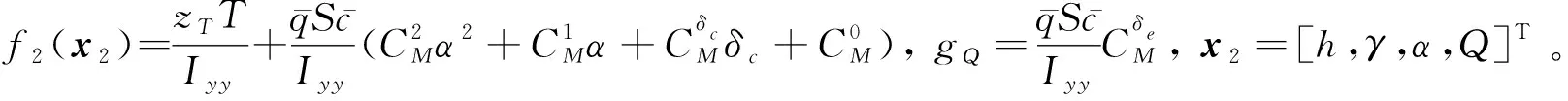
设计升降舵控制律为

(22)

其更新律设计如下：

(23)

以上完成了基本神经自适应控制的推导，在此基础上将进行离线神经网络训练并获取权值知识。

2.3 利用存储的经验知识构造在线触发控制器

对于高超声速飞行器的远程控制阶段，调用存储的经验知识，构建通信资源占用较低的在线触发控制器。在给出控制器设计过程之前，给出以下假设：

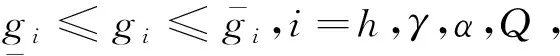
随后，对于(h-γ)子系统设计虚拟控制律及更新律设计为

(24)

设计基于事件触发的鸭翼偏角实际控制律δc为

(25)

对于(α-Q)子系统，设计虚拟控制律及更新律为

(26)

设计基于事件触发的升降舵偏角实际控制律δe为

(27)

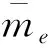
注2.与文献[9]相比，本文所提出的基于事件触发的确定学习控制器式(24)～(27)所需的在线计算量更少，更加易于实施。此外，由于事件触发机制的引入，能够使系统在获得较好的暂态跟踪性能的同时，节省控制器-执行器信道间的通信资源。

3 稳定性分析

为保证所设计控制器的收敛性，基于李雅普诺夫稳定性分析保证系统有界性。分析和相关引理如下。

引理 3[23].对于任意的κ>0和φ∈R，如下不等式成立：

(28)

定理 1.对于本文研究的高超声速飞行器高度子系统，在假设1以及虚拟控制器(24),(26)，实际控制器及事件触发条件(25),(27)的作用下，通过选择适当的设计参数，闭环系统中的所有信号是最终一致有界的，且能够排除芝诺现象。

证.选取如下李雅普诺夫函数：

(29)

对于鸭翼偏角指令，由事件触发条件式(25)可得，在区间t∈[tk,tk+1)中存在如下关系：

vc(t)=(1+βc1(t)mc1)δc(t)+βc2(t)mc2

(30)

式中：βc1(t)和βc2(t)为满足|βc1(t)|≤1和|βc2(t)|≤1的变量。因此可以得到

(31)

(32)

(33)

(34)

相似地，对于升降舵偏角指令可以得到

(35)

因此，结合式(24)和(26)，LA的导数可表示为

(36)

进而，结合引理2以及杨氏不等式，并应用如下的不等式：

(37)

可得

(38)

接下来，将证明所提出的方案可以避免芝诺现象，即触发事件不会在有限时间内无限次触发。为了实现这一目标，只需证明存在一个常数t*满足∀k∈+,tk+1-tk≥t*。对于(h-γ)子系统，由Ec(t)=vc(tk)-δc(t), ∀t∈[tk,tk+1)，可得

(39)

4 仿真校验

以第1.1节纵向运动模型(1)作为被控对象，分别按照以下几个步骤对所提控制方案进行仿真研究。首先利用第2.1节的方案进行速度子系统强化学习训练，然后利用第2.2节的离线学习方案进行训练并获取经验知识，最后利用第2.3节的触发控制方案进行验证。

4.1 利用存储的经验知识构造在线触发控制器

在训练过程中，Actor和Critic网络均采用3×64×128×1的全连接结构，超参数选取如表1所示，隐藏层激活函数为线性修正单元(Rectified linear unit, ReLU)函数，动作网络均值激活函数为双曲正切函数。

表1 PPO算法超参数设置Table 1 Hyperparameter settings of the PPO algorithm

4.2 离线训练与知识获取

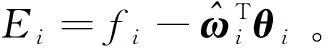
为了更清晰地展示训练效果，图2展示了离线训练100 s内的输出跟踪曲线和神经网络逼近效果。图2(a)给出了训练过程中高度的跟踪效果，可以看出经过一个暂态过程，高度状态可以很好地跟踪参考信号。图2(b)描述了所定义的训练效果，神经网络具有较好的收敛效果，因此可以根据式(25)来存储控制过程中的经验知识。

4.3 对比仿真

本部分将对比文献[9]中的神经自适应方法控制效果从而验证文中提出控制方案的有效性及优点。图3～图6展示了两种方案对比的仿真结果。其中，图3给出了速度与高度跟踪的效果对比，两种方法均能够实现对参考指令的跟踪，本文的方案具有更高的跟踪精度。图4(a)(b)(c)分别给出了速度子系统和高度子系统控制输入曲线。图5给出了姿态角变化曲线。图6描述了由控制器到执行器间的触发情况，可以看出在事件触发机制的作用下，所提方案可以在一定程度上减少触发次数，从而节省通信资源。表2展示了本文方法和对比方法在触发次数以及CPU耗时方面的对比结果。通过表2可知，由于学习控制的过程中不需要对神经网络权值参数进行在线调节，计算量大大降低，通信资源占用更少，所提的学习控制方法节约了近4/5的计算时间。

图3 速度和高度跟踪效果Fig.3 Velocity and altitude tracking performances

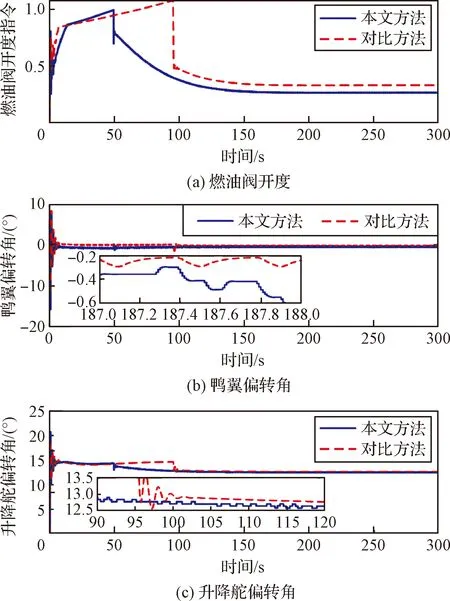
图4 控制输入曲线Fig.4 Curves of the system inputs

图5 姿态角变化曲线Fig.5 Curves of the attitude angles

图6 事件触发时间间隔Fig.6 Curves of the event interval time

表2 性能对比Table 2 Performance comparison

5 结 论

针对吸气式高超声速飞行器的飞行控制问题，本文提出一种基于学习的智能控制方法，将离线学习训练获取的智能体和经验知识应用于在线控制，分别解决了输入受限下的速度跟踪控制问题和有限通信资源条件下的高度跟踪控制问题。利用李雅普诺夫理论证明了该控制器能够保证高度跟踪误差收敛到零的小邻域内，且不会发生芝诺现象。仿真结果验证了此方案能够在节省通信资源、减少算法计算量的同时，实现良好的飞行跟踪效果。