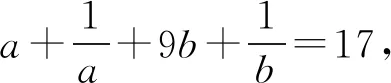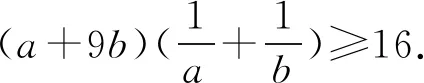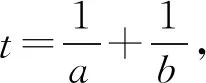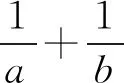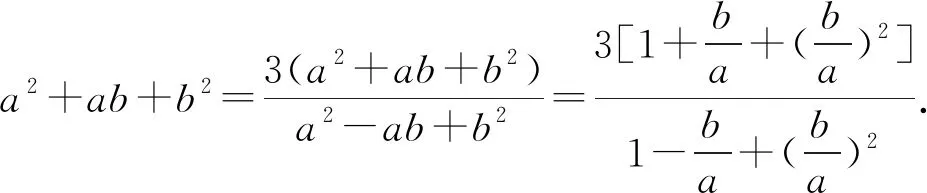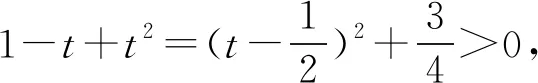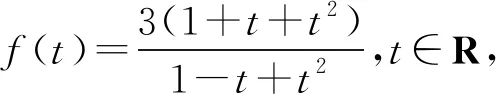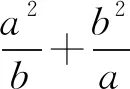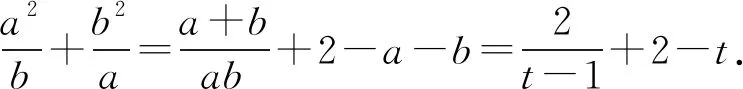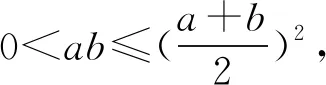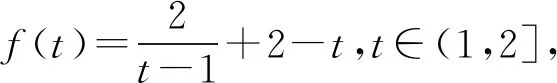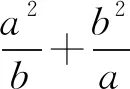主元法在不等式中的应用
2023-03-18邓启龙
邓启龙
(广东省中山纪念中学 528454)
主元法是指在一个多元数学问题中,以其中一个变量为主元,将问题转化为该主元的函数、方程或不等式等来解决问题.主元若选择得当,解题思路会变得清晰,问题将迎刃而解.选定主元后,从该主元去分析和研究,沟通问题的条件和结论,可解决许多用常规方法难以解决的问题.
1 选低次元为主元
若问题中含有二次元和三次元等高次元,可以选取低次元为主元,一般选取二次元.
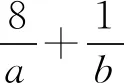
分析在条件式a+4b=a2b3中,变量a,b的次数分别是二次和三次.由于a的次数更低,所以选a为主元,将条件式a+4b=a2b3变形为关于a的一元二次方程b3a2-a-4b=0.
解析选a为主元.
由a+4b=a2b3,得b3a2-a-4b=0.
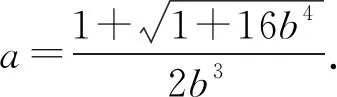
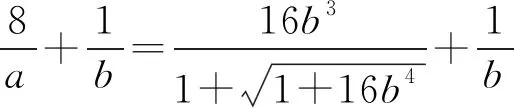
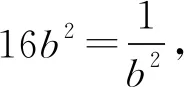
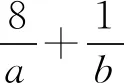
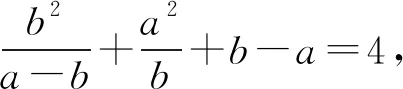

解法1 选b为主元.
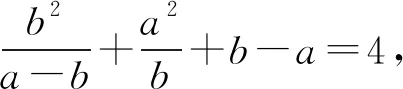
a3-2a2b+2ab2+4b2-4ab=0.
于是2(a+2)b2-2a(a+2)b+a3=0.
由b≠0,b≠a,得
解得-2 当a=2时,b=1. 所以a的最大值是2. 解法2选b为主元. 由均值不等式,得 解得-2 当a=2时,b=1. 所以a的最大值是2. 若问题中所含多个变量的次数相同,可任选一个变量为主元. 例3若不等式a2+8b2≥λb(a+b)对任意a,b∈R恒成立,求实数λ的取值范围. 分析条件式a2+8b2≥λb(a+b)中,变量a,b的次数都是二次,可选a或b为主元. 解析选a为主元. 由a2+8b2≥λb(a+b),得 a2-λba+(8-λ)b2≥0. 于是Δ=λ2b2-4(8-λ)b2 =(λ2+4λ-32)b2≤0. 整理,得λ2+4λ-32≤0. 解得-8≤λ≤4. 所以数λ的取值范围是[-8,4]. 解法1选a为主元. 4ba2+(4b2+1)a-b=0. 解法2选b为主元. 例5设a,b,c∈(-1,1),证明:ab+bc+ca+1>0. 证明选c为主元. 令f(c)=(a+b)c+ab+1,c∈(-1,1). 若a+b≥0,则f(c)>f(-1)=ab-a-b+1=(a-1)(b-1)>0. 若a+b<0,则f(c)>f(1)=ab+a+b+1=(a+1)(b+1)>0. 综上可得,ab+bc+ca+1>0 证明选a为主元. 若问题中含有多个变量,选某个变量为主元,形式简单,结构容易处理和变形,而选其他变量为主元,形式复杂,很难处理,则选该变量为主元. 分析若选a为主元,形式复杂,很难处理,而选b为主元,结构b(a-b)既可以按二次函数来处理,也可以用均值不等式来放缩,所以应选b为主元. 解析选b为主元. 由均值不等式,得 解析选b为主元. 由柯西不等式,得 解析选a为主元. 由均值不等式,得 两边平方得6a2-6a+1<0, 若问题中含有多个变量,但是选任一变量做主元都不易处理和变形,此时可构造一个新变量,例如和值、比值、差值等,然后以新变量为主元. 解析由均值不等式,得 当且仅当a=3b时取等号. 于是t(17-t)≥16. 即t2-17t+16≤0,解得1≤t≤16. 例11设a,b∈R,且a2-ab+b2=3,求a2+ab+b2的取值范围. 解析由a2-ab+b2=3,得 由a2-ab+b2=3,得a2(1-t+t2)=3. 若t=0,则f(0)=3. 若t≠0,则 综上可得,1≤f(t)≤9. 所以a2+ab+b2的取值范围是[1,9]. 解析由a+b=a2+b2,得 令t=a+b>0,由a+b=a2+b2=(a+b)2-2ab, 解得1 当t=2时,a+b=2且ab=1, 解得a=b=1. 当a=b=1时取到.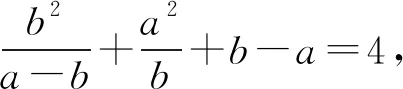
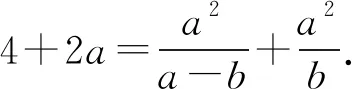
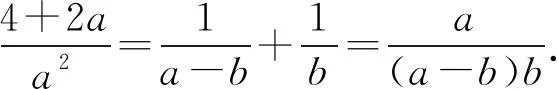
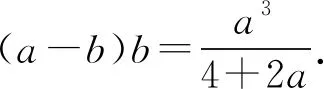

2 次数相同时任选一元为主元


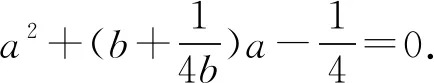
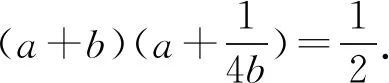
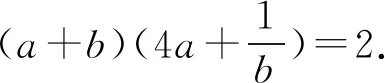


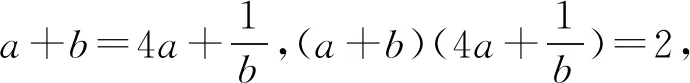
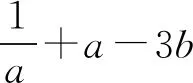

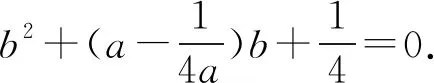
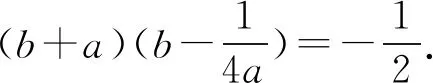
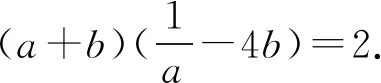
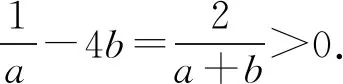

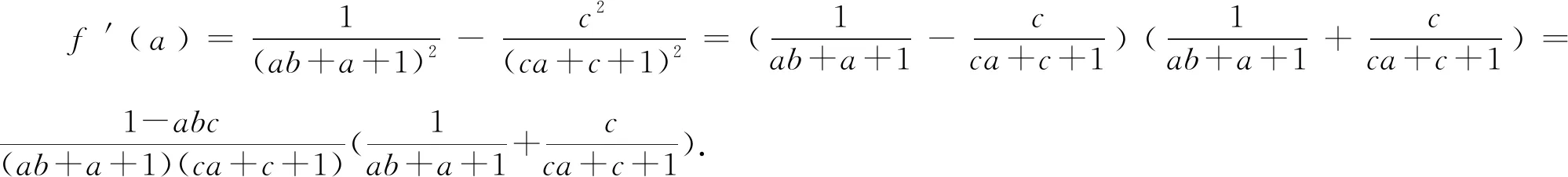
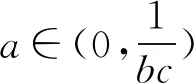
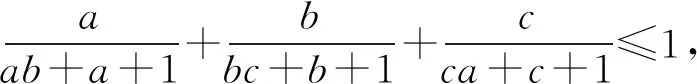
3 选易处理的变量为主元
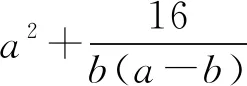

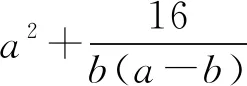
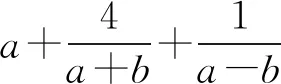
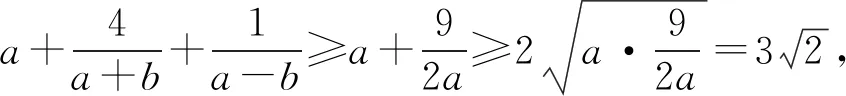
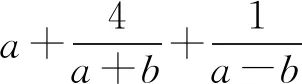
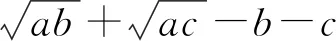

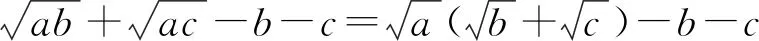
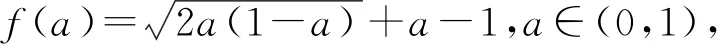
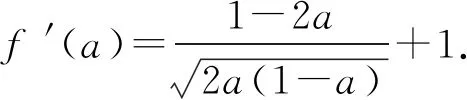
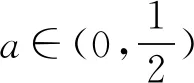
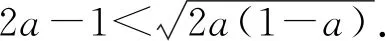
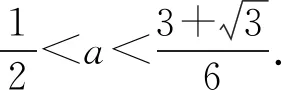
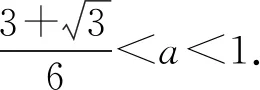

4 构造新变量为主元