Electron sheaths near a positively biased plate subjected to a weak electron beam
2023-03-15QiLIU刘琦ZianWEI卫子安JinxiuMA马锦秀KaiyangYI弋开阳WanTAO陶万andZhengyuanLI李政元
Qi LIU (刘琦), Zian WEI (卫子安), Jinxiu MA (马锦秀),*, Kaiyang YI (弋开阳),Wan TAO (陶万) and Zhengyuan LI (李政元)
1 School of Physical Sciences, University of Science and Technology of China, Hefei 230026, People's Republic of China
2 Department of Plasma Physics and Fusion Engineering,University of Science and Technology of China,Hefei 230026, People's Republic of China
3 Southwestern Institute of Physics, Chengdu 610041, People's Republic of China
Abstract Electron sheaths have previously only been measured near a positively biased small electrode,in which a potential dip was often observed.In this paper,we present an experimental study on the electron sheath near a stainless steel plate in the presence of a weak electron beam.It is shown that the electron beam,though its density is much lower than that of the background plasma,will substantially alter the sheath structure,i.e.,it causes the disappearance of the potential dip when the beam energy just exceeds the ionization potential of the neutral gas but later enhances the dip for higher energies.It is also shown that proper biases on the plate and chamber wall are the key to the formation of the electron sheath and the dip.For a fixed plate bias but with different electron beam energy,the measured thickness of the ion-free Child-Langmuir sheath agrees well with that of the theoretical model.
Keywords: electron sheath, potential dip, electron-beam-plasma system
1.Introduction
Sheaths are non-neutral regions in plasma boundaries connecting to a wall or an electrode and have been widely studied since the 1920s [1-3].The sheaths are usually classified as electron and ion sheaths according to potential distributions[4].The ion sheaths are more commonly encountered both in laboratories and in nature.However, electron sheaths usually occur near a small electrode that is biased positively with respect to the plasma potential [5-7].Under the same experimental conditions, the electron sheaths are often much thinner than the ion sheaths,which makes the measurement of the electron sheaths more difficult [8-12].
Previous experiments have shown that the potential distribution of the electron sheath was not monotonic, but often accompanied by a potential dip between the sheath and bulk plasma [5, 13-15].The sheath with the potential dip was also known as a double sheath,which is a kind of double layer since it consists of two regions of opposite space charge.Studies of the double sheath have attracted much interest over the past decade.There were also some studies on the sheath structures being influenced by injecting extra directional particles into the boundary of the electrode.For example, Fujita et al studied the V-shaped potential distribution near a grid due to electron beam injection [16].Bailung et al studied the effect of an ion beam on the electron sheath near a small plate in an ion-beam-plasma system[14].However, it is not clear how the electron sheath could form near an electrode immersed in an electron-beam-plasma system and how the electron beam affects the sheath structure.
Past observations of the electron sheath were only made near a sufficiently-small positively-biased electrode, which was usually covered with a ceramic coating on the back.The existence of the previously measured potential dip was once explained by an ‘ion pumping mechanism’ [13, 17, 18].Because of the ionization process within the sheath, the generated ions will be trapped in the dip, but the generated electrons will be accelerated toward the electrode.Thus, the accumulation of positive charge will prevent the formation of the stationary sheath.To explain the observed stationary dip,Forest and Hershkowitz[13]once measured the equipotential contours near the electrode and found a potential drop near the edge of the electrode because the back side of the electrode was electrically floated at a negative potential.Thus,they proposed the removal (pumping) of the trapped ions along the surface to the edge of the electrode, which is, in fact, a 2D process.However, in many low-pressure discharges, the collision mean-free-path for the ionization is much longer (about the size of the discharge chamber) than the sheath thickness.Thus, the ion pumping might not be applicable to the low pressure discharges.
Recently, Baalrud et al proposed a new model of global nonambipolar flow to explain under what conditions a monotonic electron sheath, a monotonic ion sheath, or a nonmonotonic(double)sheath could form[5]for the simplest case of the plasma consisting of a wall and a planar auxiliary electrode.They found that the area of the auxiliary electrode is a key parameter in determining which kind of sheath could form near it.If the area ratio of the auxiliary electrode to the wall is greater than 1.7μ, whereμ= (and meand miare the electron and ion mass, respectively, a monotonic ion sheath will form near the auxiliary electrode regardless of its bias.If the area ratio is less than μ, a monotonic electron sheath can form when the auxiliary electrode is biased at least a few volts more positive than the plasma.If the area ratio is between μ and 1.7μ, a double sheath (potential dip) will form near the auxiliary electrode.The act of the potential dip is to reflect some random electron flux back to the bulk plasma in order to keep the global balance of the electron and ion currents to the wall and to the auxiliary electrode.This model was verified in hot filament and hollow cathode discharges in recent experiments[5, 6, 19, 20].
Another difficulty in the study of the electron sheath is that the positive bias on the electron-collecting electrode will significantly alter the plasma parameters, and in particular,raise the plasma potential.The bias of the electrode is relative to grounded chamber walls, which means that the potential drop from the electrode to the bulk plasma is a variable.However, the effect of the potential drop was not taken into account in previous experiments.
In this work, we experimentally investigate the electron sheath formation near a positively biased plate immersed in a weak electron-beam-plasma system.It will be shown that the presence of the electron beam,though weak,will appreciably modify the electron sheath structure.The experimental arrangement is described in section 2.The formation of the electron-beam-plasma system and the measured plasma parameters are given in section 3.The electron sheath structures are presented in section 4.The main conclusions are summarized in section 5.
2.Experimental setup
The experiment was carried out in a double plasma device,which is schematically shown in figure 1.The device consists of two identical cylindrical chambers of 500 mm length and 500 mm diameter insulated from each other.The base pressure is p=2×10-4Pa and the working pressure is p=2.5×10-2Pa with Ar gas injected.Two separation grids,SG1 and SG2, with 60% geometric transmittance, were placed in parallel between the chambers.The plasma-generating part(in the source chamber)consists of an anode mesh(AM) and a hot cathode composed of 12 tungsten wires (hot filament, HF) of 120 mm length and 0.2 mm diameter.The plasma was produced with the discharge between the AM and HF.The discharge voltage and current are 30 V and 48 mA,respectively.The bulk plasma parameters in each chamber were diagnosed with two identical stainless steel planar Langmuir probes (10 mm diameter and 0.5 mm thickness,located 140 mm to the separation grids).The typical plasma parameters in the experimental chamber are electron density ne=(1-2)×1014m-3and temperature Te=3-4 eV.A stainless steel circular plate (80 mm in diameter, positively biased)was placed in the center of the experimental chamber for the purpose of the electron sheath formation.An axially movable emissive probe was used to measure the plasma potential distribution in the upstream side of the plate.

Figure 1.Schematic diagram of the experimental setup.AM: anode mesh, HF: hot filaments, PP: planar probe, EP: emissive probe.
The diagnostics using Langmuir probes are typical invasive methods,which were previously applied to diagnose some sheath-related properties,for example,the thickness of a collisional pre-sheath[21]and the expansion of a sheath[22].The size of the cold Langmuir probes is usually about (or even larger than) the sheath thickness.Thus, the interference of the cold probes with the sheath results in significant measurement deviation from reality [23].Hot (emissive)probe [24] diagnosis has become the most common method for the sheath diagnosis.The fine structured emissive probes(with sizes much smaller than the dimension of the sheath)were widely used in the studies of both the ion and electron sheaths [5,14,25-28].The emissive probe used in this work consists of a probe tip made of tungsten wire 0.025 mm in diameter and 5 mm in length (positioned with its length parallel to the surface of the plate) and lead wires insulated and supported within glass capillary tubes of 0.32 mm in diameter.The details of the probe structure can be found elsewhere [25].The resistance of the emissive probe is 1.5 Ω(including lead wires and connections)and the heating current is 230-240 mA.The spatial resolution of the probe movement is 0.02 mm.The plasma potential is measured using the inflection-point method from the probe I-V trace in the zeroemission limit [24].
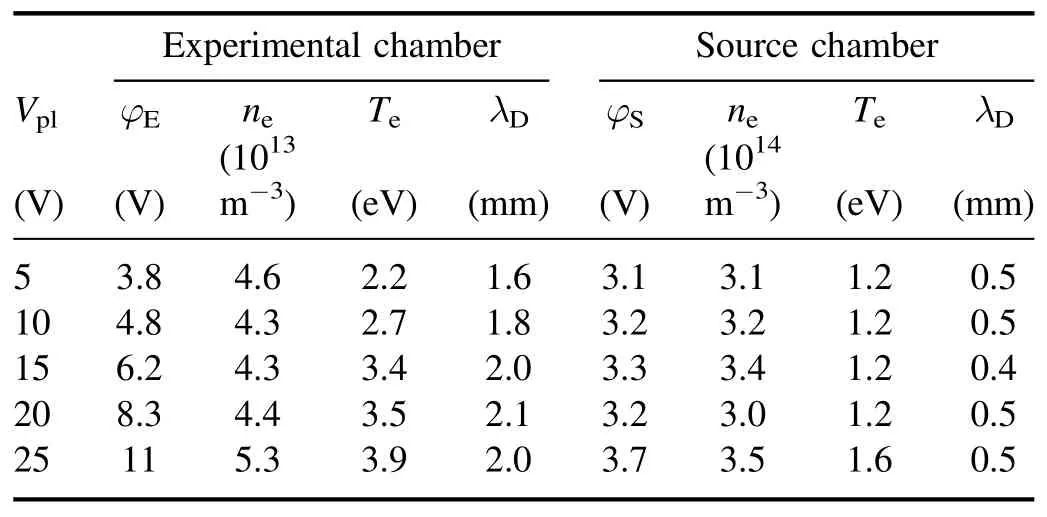
Table 1.Dependence of the plasma parameters on the bias of the plate, Vpl.The source and experimental chamber walls as well as SG1 and SG2 are grounded.
3.Formation of electron-beam-plasma system
Previous experiments showed that an ion-beam-plasma system with a large proportion of beam ions can be easily obtained in the double-plasma device [26, 29].To keep the experiment as stable as possible, both SG2 and the experimental chamber were grounded.To form an electron-beamplasma system, a necessary condition is that the potential of the experimental region must be higher than that of the source region.Two ways were used to control the electron beam energy by adjusting the potential difference between the experimental and the source regions.
First, we investigated the influence of the plate bias, Vpl,on the plasma parameters while keeping the source chamber and SG1 grounded.A positive bias Vpl=5-25 V with respect to the ground was applied to the plate.The electron density ne,temperature Teand the plasma potentials φSand φEin the bulk plasmas of the source and experimental regions, measured with the planar Langmuir probes, together with the calculated Debye lengths λD,are listed in table 1.It is shown that the plasma parameters in the source region remain almost unchanged.In the experimental region,the changes in ne,Te,and λDare very small, but the plasma potential φEincreases with the increase of Vpl.It should be noted that the increase of φEis not linear with Vpl.When Vplexceeds 30 V,φEis raised close to the bias of the plate.
It can be seen from table 1 that the plasma potential is higher in the experimental region than that in the source region.Thus, the electrons gain energy traversing from the source region through SG1 and SG2 into the experimental region,forming an electron beam.Since the plasma is weakly collisional in this device (collision mean-free-path is comparable to the size of the chambers),the energy of the electron beam, Eb, is approximately equal to the potential difference between the experimental and source region, i.e.,Eb≈e(φE-φS).Figure 2 shows the dependence of the potential drops φE-φSand Vpl-φEon the plate bias Vpl.It is shown that the electron beam energy increases with Vpl.Furthermore, the bias on the plate is higher than the plasma potential φE.Therefore, the electron sheath forms near the plate and the potential drop across the sheath increases with the increase of Vpl.
Second, we keep the plate bias fixed at Vpl=20 V and change the negative bias,VS,on the source chamber wall and SG1(SG1 is connected to the source chamber)while keeping the experimental chamber and SG2 grounded.In this case,the measured plasma parameters are listed in table 2.It can be seen that the changes in ne,Te,and λDin the source chamber are very small except for the VS=0 case, and the changes in the experimental chamber are not appreciable, especially when VS≤-10 V.With the decrease of VSfrom 0 to-80 V,the plasma potential in the experimental region,φE,shows an initial increase of about 4 V and then remains almost unchanged after VS≤-10 V.However, the plasma potential in the source region, φS, decreases with VS, but φSis always about 4 V higher than VSexcept for VS=0 case.Figure 3 shows the dependence of the potential drops φE-φSand Vpl-φEon the bias VS.It is shown that φE-φS(i.e., the electron beam energy) decreases almost linearly with the increase of VS.The potential drop Vpl-φEonly shows a very slight decrease when VSchanges from -80 to -20 V and then a small increase after VS>-20 V.
From the above results it can be seen that the potential difference between the experimental and source regions accelerates the electrons to form a beam.The beam electrons ionize the neutral gas to create a background plasma.Thus,the electron-beam-plasma system establishes in the experimental region.However, since the plasma potential in the source region is higher than the bias on SG1, most of the electrons from the source region are reflected by the potential barrier of SG1.Only a few electrons enter into the experimental region.Therefore, the electron beam is weak.This is manifested by the current-voltage trace of a spherical probe of 8 mm diameter inserted into the experimental region (about 100 mm from the SG2)as shown in figure 4(a)for the case of VS=-40 V and Vpl=20 V.The main knee position(inflection point) is near the spherical probe bias Vsp~15 V,corresponding to the bulk plasma potential of the experimental region.There is a second knee at Vsp~-39 V as shown in the magnified portion of the I-V trace in the inset of figure 4(a), which corresponds to the contribution from the electron beam.The difference between the two knee points(~44 V) corresponds to the electron beam energy.The soobtained beam energy is close to the plasma potential difference between the experimental and source regions(~39 V)measured with the planar probes.Note that there exist slight differences in the measured results among the spherical and planar probes and that the plasma potentials in the source and experimental regions are measured not with a single planar probe.The collected current from the electron beam to the spherical probe can be estimated by the current difference between the two tangents near the second knee[30]as shown in the inset of figure 4(a).The inferred beam-to-background density ratio, nb/ne=(vte/vb)(Ib/Ie) (vb, vte, Ib, and Ieare the speeds and the probe collected currents of the beam and thermal electrons,respectively)versus the potential difference φE-φSis shown in figure 4(b).It shows only a slight increase in nb/newhen the beam energy increases from 20 to 80 eV.nb/neis only about ~0.2%for most cases.Though the concentration of the electron beam is rather low, it has an appreciable effect on the sheath structure,as will be shown in the next section.

Figure 2.Variations in the potential drop from the plate to the bulk plasma Vpl-φE in the experimental region and the plasma potential difference φE-φS between the experimental and source regions with respect to the bias on the plate Vpl.Both chamber walls and SG1 and SG2 are grounded.

Figure 3.Variations in the potential drop from the plate to the bulk plasma Vpl-φE in the experimental region and the plasma potential difference φE-φS between the experimental and source regions with respect to the bias on the source chamber wall VS.The plate bias is Vpl=20 V.

Table 2.The dependence of the plasma parameters on the bias of the source chamber wall and SG1, VS.The experimental chamber and SG2 are grounded and the plate is biased at 20 V with respect to the ground.
4.Potential distribution of the electron sheaths
For the case when both the source and experimental chambers are grounded, the potential distributions with respect to the distance from the plate for different plate biases are shown in figure 5.It is shown that the electron sheath structures are nearly monotonic in this case.As the plate bias increases,both the sheath potential drop and the electron beam energy increase (see also figure 2 and table 1), and thus the electron sheath thickness increases.
For a given bias on the plate, Vpl=20 V, and different negative biases on the source chamber, the potential distributions with respect to the distance from the plate are shown in figure 6.As shown in the figure, when VS=0, the electron beam energy is low (see figure 3 and table 2) and there exists an obvious potential dip structure near the plate.As VSdecreases to -20 V, the dip structure weakens and almost disappears.With a further decrease in VS, the dip structure reappears and gradually enhances.
For convenience of discussion, we define a few characteristic quantities as schematically shown in figure 7.We define the position of the potential minimum as the dip position,xdip,and the corresponding potential difference from the bulk plasma to the dip as φdip.The position where the potential starts to deviate from the bulk plasma is defined as the sheath edge, xs.The inflection point, xinfl, at which the charge neutrality satisfies (d2φ/dx2=-ρ/ϵ0=0, where ρ is the net charge density and ϵ0is the vacuum dielectric constant),is defined as the interface between the electron and ion sheaths.The region between xinfland the plate is a negative charge layer(electron sheath)and that between xsand xinflis a positive charge layer(ion sheath).In the case when there is no potential dip structure,the inflection point and the sheath edge should coincide, i.e., xinfl=xs.Because for this kind of discharge the ion temperature (close to room temperature) is much lower than the electron temperature, all ions are essentially reflected by the positive sheath potential with respect to the bulk plasma potential.Hence, the point in the region between the dip and the plate where the potential is equal to the bulk plasma potential, xCL,can be defined as the edge of the electron Child-Langmuir sheath since the ion density can be neglected in the region between x=xCLand x=0.

Figure 4.(a)Current-voltage trace of the 8 mm diameter spherical probe.The inset is a magnified portion of the trace near the second knee.(b)Beam-to-background electron density ratio,nb/ne,inferred from the second and main knees of the I-V trace,versus the bias on the source chamber wall.

Figure 5.Potential distributions near the positively biased plate in the upstream side for different bias voltages on the plate.x=0 is the position of the plate.The source and experimental chambers and SG1 and SG2 are grounded.

Figure 6.Potential distributions near the positively biased plate(Vpl=20 V) in the upstream side for different bias voltages on the source chamber and SG1.x=0 is the position of the plate.The experimental chamber and SG2 are grounded.The lines are the polynomial fits to the experimental data.
Using the analog to the electron-free Child-Langmuir law, the ion-free Child-Langmuir law can similarly be obtained.The relationship between the thickness of the Child-Langmuir sheath, wCL, and the sheath potential drop from the plate bias Vplto the Child-Langmuir sheath-edge potential (equal to the bulk plasma potential of the experimental region φE) can be written as [31]
where λDis the electron Debye length evaluated at the sheath edge.Figure 8 presents a comparison of the thickness of the Child-Langmuir sheath, |xCL|, obtained from the measured potential profiles,with that evaluated from equation(1),wCL,using the bulk plasma parameters obtained in section 3, versus the potential difference φE-φS.Good agreement between the measured and the theoretically evaluated Child-Langmuir sheath thicknesses is observed.However, the experimental Child-Langmuir sheath thickness is systematically larger by about 1 mm than the theoretical thickness.

Figure 7.Schematic drawing of the electron sheath with the potential dip showing the characteristic points.xs is the edge of the sheath with the bulk plasma, xinfl is the inflection point separating the ion and electron sheaths, xdip is the point of the potential minimum, xCL is the edge of the ion-free Child-Langmuir sheath, and φdip is the potential difference between the bulk plasma and the potential minimum.

Figure 8.Comparison of the measured (|xCL|, bullets) and the theoretically evaluated (wCL, closed circles) ion-free Child-Langmuir sheath thickness versus the potential difference φE-φS.
In the presence of the potential dip, the variations of the depth φdipand the width xCL-xsof the dip together with the whole thickness of the electron sheath |xinfl| with respect to the electron beam energy, ~e(φE-φS), are shown in figure 9.It is shown that with the increase of the beam energy,the dip depth suddenly drops to almost zero and then slowly increases and saturates at about 0.2 V.The dip width and the whole electron sheath thickness show similar variations.

Figure 9.Variations in the depth φdip (a), the width xCL-xs (b) of the potential dip,and the whole thickness of the electron sheath|xinfl|(c) with respect to the potential difference φE-φS.
To explain the experimental results, we make use of the balance between the loss and generation of the charged particles [5].For simplicity, we only consider the balance in the experimental chamber.Since the potential of the bulk plasma is higher than the grounded chamber wall and the bias on the planar plate is higher than the bulk plasma potential, the ions are mainly lost to the chamber wall and the background electrons are mainly lost to the plate because they are reflected by the corresponding potential barrier.The beam electrons, on the other hand, can be lost both to the chamber wall and to the plate because of their higher energy to penetrate the barrier except for the case when VS=0.The charged particle generation in the experimental chamber is due to the ionization of the neutral argon gas by both the thermal electrons and the electron beam.In the presence of the potential dip near the plate, the balance of the electrons and ions can be written in a simplified form
where G represents the generation of the charged particles,Apland Aware the areas of the plate and chamber wall, respectively, nband vbare the density and velocity of the electron beam,is the mean speed of the background electrons,is the ion-acoustic speed,and α accounts for the correction of the ion loss flux due to the presence of the electron beam.The quasi-neutrality condition requires ni=ne+nb.From equations (2) and (3), and noting Apl≪Awandwe obtain the depth of the dip
Equation (4) shows that the presence of the electron beam deepens the potential dip.Note that when VS=0 or-5 V (the first two data in figure 9), the energy of the electron beam is lower than the ionization potential of the Ar gas(15.6 eV),so that no loss of the beam electrons due to the ionization occurs.In this case, the fraction of the beam electrons is relatively high and hence the dip is relatively deep.When VS=-10 V,the energy of the electron beam is Eb~17.9 eV,which is higher than the ionization potential, and hence the impact ionization by the beam electrons takes place,which is evidenced by the sudden increase in the background electron density (from 0.7×1013to 1.3×1013m-3) as observed in table 2.In this case, the beam electrons are substantially consumed and nb/neis substantially lower than the case when VS>-10 V.This explains the sudden decrease in φdiptill Eb~17.9 eV.The ionization process is further enhanced until VS=-20 V (the background electron density is further increased from 1.3×1013to 1.8×1013m-3),after which the ionization seems to be saturated (the background electron density is around 2×1013m-3,see table 2).This can also be seen in figure 4(b) where nb/neis about 0.2%.However, the beam energy increases in this process.Thus,the increase in vbcan explain the slow increase in φdipafter Eb>17.9 eV.
5.Discussion and conclusion
In this paper, the formation of the electron-beam-plasma system and its influence on the electron sheath near a positively biased plate were studied in the experimental chamber of a double-plasma device.It was shown that the large-area(about the cross section of the device) and low-energy electron beam can be introduced by means of adjusting the biases on the plate and on the source chamber wall.Though the concentration of the electron beam is small,it has a significant effect on the electron sheath.
For the case when both the source and experimental chambers are grounded,raising the bias on the plate results in the increase both in the electron sheath potential drop and in the electron beam energy.In this case, the electron sheaths near the plate are nearly monotonic and the potential dip structure is not obvious except for in the case when the bias is rather low (~5 V) when the dip structure tends to appear.
For a given bias on the plate,raising the negative bias VSon the source chamber wall results in a nearly linear increase in the electron beam energy but the sheath potential drop remains almost fixed.The presence of the electron beam enhances the dip structure, i.e., the increase in the beam energy causes the deepening and widening of the potential dip except for the initial rapid drop in the dip depth when the beam energy increases from below to above the ionization potential of the argon gas.The latter effect is attributed to the rapid loss of the beam electrons to the background electrons in the ionization process.Furthermore, the experimentally measured variation of the thickness of the ion-free Child-Langmuir sheath agrees well with that of the theoretical model.
It was previously shown that the formation of the dip structure near an electron sheath is the result of the selfadjustment of the plasma to satisfy the global balance between the fluxes of the electron and ion losses[5,6].In the presence of the electron beam, the total electron loss flux increases.Thus, it is expected that a deeper potential dip forms self-consistently to repel more thermal electrons from being lost to the plate in order to maintain the global current balance.Therefore, our experimental results showing that the dip depth increases with the beam energy are in agreement with the theoretical expectation.
The electron sheath exists widely both in laboratory plasmas and in applications, such as that near the Langmuir probe and the surface of a spacecraft.The existence of the electron beam significantly modifies the sheath properties.Thus, the investigation carried out in this work may have practical applications in interpreting the possible deformation of the collected currents of the Langmuir probe and the surface charging of the spacecraft when they are in the plasma containing the electron beam.In addition, it may also have potential applications in plasma-material processing using the electron beam.
Acknowledgments
This work is supported by National Natural Science Foundation of China (Nos.11975229 and 11705201).
猜你喜欢
杂志排行
Plasma Science and Technology的其它文章
- Application of integrated simulation environment SIEMNED to the analysis of the MEPHIST-0 tokamak operation
- Improvement of a temperature response function for divertor heat flux monitoring in fusion devices
- Degradation of sulfamethoxazole in water by dielectric barrier discharge plasma jet:influencing parameters, degradation pathway, toxicity evaluation
- Experimental investigation of dynamic stall flow control using a microsecond-pulsed plasma actuator
- Laser-assisted ablation and plasma formation of titanium explored by LIBS,QCM, optical microscopy and SEM analyses along with mechanical modifications under different pressures of Ar and Ne
- Study on the effect of focal position change on the expansion velocity and propagation mechanism of plasma generated by millisecond pulsed laser-induced fused silica
