星下点构型对目标定位精度的影响分析*

屈 瑞 宋 友 李国宾 刘志江 邓 丽 段 然

1. 北京航空航天大学软件学院，北京 100191 2. 中国科学院国家空间科学中心复杂航天系统电子信息技术重点实验室，北京 100190

0 引言

无源定位是一种在自身不发射电磁波的情况下，利用被探测目标自身所发出的信号进行定位的目标探测技术。目前基于多星系统的无源定位已广泛应用于军事和民用领域[1-3]，包括无线通信[2]、布站[4]、雷达[5]、导航等[6-8]。随着大规模卫星星座网络的发展，开展多星联合定位，有效提升定位精度越来越重要。

多星定位可以利用的参数包括到达角(Angel of Arrival，AOA)、到达时间(Time of Arrival，TOA)、到达时间差(Time Difference of Arrival，TDOA)、到达频率差(Frequency Difference of Arrival，FDOA)等。联合多种测量参数的定位体制可以融合不同参数的优势，提升对目标辐射源信号类型的适应能力，并在一定程度上提高定位精度。

HO等首次提出TDOA/FDOA算法是对运动目标进行定位的经典两阶加权的最小二乘(weighted least squares, WLS)算法[9]并推导了多星TDOA/FDOA联合定位的误差CRLB，通过此方法计算出了无偏估计器中最优无偏估计器能够产生的最小的定位误差[10]。CHOU等计算了双星联合定位的几何精度因子(geometric dilution of precision, GDOP)和方差，得出TDOA/FDOA定位曲面与地球表面夹角为直角时定位误差最小的结论[11]。常新亚等根据双星时差/频差(TDOA/FDOA)的定位原理，推导了目标定位精度模型，分析了目标定位精度与误差源之间的关系，且通过分析得知FDOA测量精度和卫星速度测量精度是影响双星定位的关键因素之一[12]。丰泽斌等在应用GPS、北斗等系统进行定位时，使用通过信号质量、仰角的选择并结合模糊综合评判的一系列选星策略，来高效选取最佳卫星组合[13]。康国华等提出了一种基于M-W组合观测值进行自适应估计观测噪声的方法，通过对观测噪声统计实时估计观测噪声[14]。任凯强等针对三星时差定位系统中，由星历误差和时间同步误差导致无法精确定位的问题，提出一种基于正交投影的两步迭代有源校正算法[15]。

上述研究侧重于定位算法的改进和优化，对星座构型特别是星下点构型对定位精度的影响分析研究较少。本文基于TDOA/FDOA对地面辐射源目标的定位原理，建立了多星TDOA/FDOA联合定位模型和定位精度分析模型。针对三星和四星系统的不同星下点构型，仿真分析了5种三星系统星下点构型和4种四星系统星下点构型的目标定位精度。

1 多星TDOA/FDOA定位的基本原理

多星TDOA/FDOA定位是通过配置有接收和处理模块的多颗卫星同时接收运动的目标辐射源的发射信号，根据信号到达不同卫星的时间差、多普勒频移差来确定目标的位置。

设地面辐射源目标的位置坐标为u。卫星的位置坐标为si，i为卫星序号，假设选取1号卫星为主参考星(以下简称“主星”)，其他星为副星，在计算TDOA与FDOA时副星均以主星为参考，卫星与目标的相对位置为ri，相对运动速度为vi。TDOA/FDOA定位原理表示如式(1)。

(1)

式中：TDOAi为主星与i号副星的到达时间差，FDOAi为主星与i号副星的到达频率差。f为探测频率，c为光速。通过卫星探测数据得到的两星之间的时差和频差，联合求解非线性方程组，计算出目标位置。该方程属于非线性的三元高次方程，一般通过数值迭代和多维搜索取得一定精度下的近似解。国内外学者提出了很多进行解算的方法，包括降元法、基于泰勒级数法的求解法、牛顿迭代求解法等。本文不对其求解方法进行讨论，主要对该方法的定位精度进行分析。

2 多星构型的定位精度分析

目标的定位精度受多种因素影响，包括星座构型、测量因素和目标辐射源本身特性，如图1所示。星下点构型主要影响基线长度和基线方向。

图1 目标定位精度影响因素

这里以三星定位为例，基于多星TDOA/FDOA定位原理，可以进一步推导出目标定位精度模型。由式(1)可知，

(2)

利用全微分法对其影响因素对定位精度的影响进行建模。对式(2)中的变量TDOA2,TDOA3,FDOA2,FDOA3,(x,y,z),(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),(vx1,vy1,vz1),(vx2,vy2,vz2),(vx3,vy3,vz3)进行一阶线性近似展开，可得其定位精度评定模型。

(3)

将式(3)改写为：

(4)

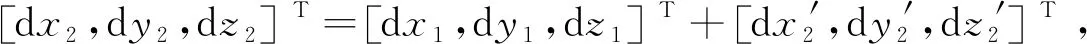
(5)

设K1=B1+B2+B3,K2=B2,K3=B3,K4=B4,K5=B5,K6=B6, 并认为两颗卫星的位置测量精度、速度测量精度、TDOA测量精度、FDOA测量精度互不相关，则利用矩阵相关运算得到：

(6)

式中：M为TDOA和FDOA测量精度的相关矩阵；Ei为位置测量精度和速度测量精度的相关矩阵。从上面的分析结果可以看出，计算定位精度需要计算TDOA和FDOA测量精度相关矩阵M、位置测量精度及速度测量精度相关矩阵Ei。

假设信号TDOA和FDOA的测量精度均值为0，且互不相关，则TDOA和FDOA的测量精度相关矩阵为：

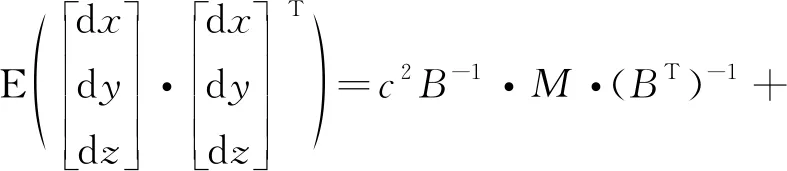
(7)

这里认为绝对位置测量精度分量 dxi, dyi,dzi是各自独立的随机变量，因此卫星不同时刻的绝对位置测量精度相关矩阵为

(8)

式中:σas为主星的绝对位置测量精度。2号副星及3号副星相对于1号主星的相对位置测量精度相关矩阵为

(9)

式中:σrs为相对位置测量精度。三星的速度测量精度相关矩阵表示为

Ei=diag(D(dvxj),D(dvyj),D(dvzj)),
i=4,5,6,j=1,2,3

(10)

式中：D(dvxj),D(dvyj),D(dvzj)分别表示1号主星、2号副星和3号副星在x、y、z方向上的速度测量精度。

目标定位精度σ用式(8)计算出的3个正交方向上的测量精度σx,σy,σz表示，即：

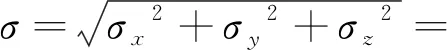
(11)

以上为三星定位系统的目标定位精度模型，四星定位系统的目标定位精度模型与之同理，这里就不再赘述。

3 仿真校验

3.1 仿真输入

仿真轨道高度600km圆轨道，波束角40°，探测区域1000km，多颗卫星近似在同一轨道面内。

各项测量精度指标为：目标辐射信号频率为3GHz，TDOA测量精度为100ns，FDOA测量精度为20Hz，速度测量精度为10m/s，绝对位置测量精度为100m，相对位置测量精度为10m。各个测量量彼此相互独立。

有效定位区域：满足目标定位精度小于或等于10km的区域。定位因子：有效定位区域占探测区域的比值。

3.2 三星构型的目标定位精度分析

对比5种典型的卫星星下点构型的定位精度分布情况，每种构型中的最长基线均为900km。5种构型星下点分布分别为直线型、顶角为30°的等腰锐角三角形、等边三角形、顶角为90°的等腰直角三角形、顶角为120°的等腰钝角三角形。

探测区域为三星定位系统中心星下点为中心，经仿真分析，其探测区域内的定位精度如图2所示，其中圆圈代表卫星的星下点位置分布，箭头表示各卫星的速度。

图2 三星不同星下点构型时探测区域的GDOP图

3.3 四星构型的定位精度分析

对比4种典型的卫星星下点构型的定位精度分布情况，每种构型中的最长基线均为900km。4种典型构型的星下点分布为：直线型、近似等腰直角三角形、等边三角形和凸四边形。仿真分析，探测区域的定位精度如图3所示，其中圆圈代表卫星的星下点位置分布，箭头表示各卫星的速度。

图3 四星不同星下点构型时探测区域的GDOP图

3.4 数据分析

经仿真计算得到的三星构型和四星构型的定位精度和定位因子如表1所示：

表1 不同构型的定位精度均值及定位因子

三星定位系统中，星下点等边三角形构型的定位精度分布最优，在定位区域内的定位有效区域达到100%，且在定位区域内的平均定位精度达到6.1m。直线型构型定位精度最差。三星星下点位置越分散，目标区域内的定位精度越高。

四星定位系统中，星下点凹四边形构型的定位精度分布最优，在定位区域内的定位有效区域达到100%，且在定位区域内的平均定位精度达到5.9m；其次是星下点凸四边形构型，在定位区域内的定位有效区域同样达到100%，在定位区域内的平均定位精度为6.3m，构型2的定位精度相对构型3和构型4较低，定位精度为7.8m。构型1直线型，存在定位盲区，且定位精度较差，有效定位区域内的定位精度为639.5m。同样可以看出，四星星下点位置越分散，目标区域内的定位精度越高。

对比四星定位和三星定位，卫星数量的增减，能提升定位精度。三星及四星定位系统中，当卫星构型为非直线型时，其定位精度能达到米级左右。在观测范围内，星下点位置越分散，目标区域内的定位精度越高。

因此，为了获得更高的精度，应该尽量应用非直线型的三星及四星定位系统对目标进行观测，同时，各卫星之间的基线尽可能拉长。

4 结论

大规模卫星星座的发展，使得目标定位精度的分析更为重要。目标定位受多种因素影响，包括星座构型、测量因素和目标辐射源本身特性。本文在假定测量因素确定的条件下，针对性地分析了多颗卫星不同星下点构型对定位精度的影响。定位卫星数量的增加，可以提高定位精度。星下点位置越分散，目标区域内的定位精度越高，尽量避免选用星下点直线型的三星及四星定位系统。在未来利用大规模卫星星座进行目标定位时，本文研究为针对性地选取可视卫星和定位精度分析提供了有效支撑。