松鼠搜索算法优化SVM的液体火箭动力系统故障诊断*

2023-03-13陈占国

航天控制 2023年1期

陈占国薛薇许亮

1.天津理工大学电气工程与自动化学院天津市复杂系统控制理论与应用重点实验室，天津 300384 2.中国航天科技创新研究院，北京 100083

0 引言

在上世纪，红线阈值系统是火箭发动机的主要保护系统，如果测量值超过了几个参数中的任何一个预先确定的运行限制，就会发出引擎关闭信号，从而关闭发动机引擎。对于航天飞机主发动机(SSME)，在主级期间会监控7个关键的发动机参数，这些参数的限值被设定在影响发动机安全运行的水平。然而，仅依靠这一系统，就会导致发动机过早熄火，原因是正常的漂移可能引起红线参数的变化。因此为了进一步加强安全监测，并实现更早的故障检测，90年代NASA提出了火箭发动机健康管理系统(HMSRE)的框架。HMSRE能够解决现有系统无法充分检测到故障模式的问题，使发动机受到最小的损伤，得到最大的收益。

2002年，国防科技大学的赵永学等[1]提出了基于羽流发射光谱的故障检测技术。这项技术有非接触和高灵敏度等特点，适合作为发动机的健康监控及故障诊断技术。2003年，哈尔滨工业大学龙兵等[2]研究了航天器集成健康管理的基本概念，提出了航天器健康管理系统的开发方案。

近年来，利用神经网络、聚类分析、模糊数学、专家系统、云计算方法等技术进行故障检测与诊断的研究取得了优异的成绩[3]。2009年李睿等[4]结合虚拟仪器语言和快速原型化技术的优点，构建了航空发动机故障诊断算法仿真平台，有效解决了故障算法硬件在回路仿真过程中存在的一些问题。2010年黄强等[5]研究了基于云-神经网络的液体火箭发动机故障检测方法，但是基于神经网络的故障检测方法需要大量数据进行训练，而实际样本数据往往十分有限。2011年窦唯等[6]针对涡轮泵故障诊断方法只能在有样本数据并且样本数据充足的情况下才能进行准确诊断的缺点，提出一种适用于涡轮泵在线监测及诊断的方法，可用于故障样本少的航空航天设备的故障检测。2011年尹俊等[7]对卡尔曼滤波故障诊断方法和神经网络故障诊断方法进行融合从而提高了故障诊断的准确率和可靠性。2016年吴建军等[8]提出了利用动态云反向传播神经网络进行液体火箭发动机故障诊断的方法，优点是可正确检测和分类故障，对噪声具有较高的鲁棒性，同时运行时间短，满足液体火箭发动机故障诊断的实时性要求。2020年Park等[9]将深度学习用于液体火箭发动机故障检测与诊断中，该方法有较好的分类性能和较强的适用性。2020年董周杰等[10]提出了一种基于数据驱动的综合模糊聚类算法用于液体火箭发动机故障诊断，能够准确及时地检测出故障并隔离故障。2021年王珺等[11]提出了一种卷积自编码器的液体火箭发动机健康状态智能检测方法，该方法能够监测整机及各部件的健康状态和退化趋势，但是准确率稍低。2022年赵万里等[12]提出了一种基于时间序列分析的故障诊断方法，该方法可对故障的传感器进行有效判断，同时运行时间短，具有良好的工程应用价值。2022年杨懿等[13]利用Hilbert-Huang变换进行液体火箭发动机涡轮泵的故障分析，该方法可分析火箭发动机和其他组合件的试验数据并对故障定位。

上述方法都比传统的红线阈值监测进步了很多，体现了不同程度的智能、鲁棒和准确等性能，是现代智能方法在火箭动力系统故障检测中的成功应用。但是现今的智能算法大多都存在需要充足故障训练样本、预测时间长、分类准确率有待继续提高等问题。针对以上问题，本文提出了一种实时性好、准确略高、需求样本少的具有工程应用价值的故障诊断方法。

由于智能优化算法原理和机理的不同，其结果在不同的应用中会有差距。在实践中，选择与支持向量机相结合的优化算法值得考虑。PSO算法是Kennedy等[14]观察追踪鸟群捕食情况提出的全局搜索算法，PSO-SVM模型即采用粒子群算法对支持向量机的惩罚因子和核函数参数进行优化的模型。相较于PSO-SVM模型容易陷入局部最优的缺点，松鼠搜索算法优化(SSA)是一种新的优化算法，算法中加入了季节性监测条件，用松鼠搜索算法优化与支持向量机结合，有助于避免寻优计算陷入局部极值，同时使模型具有收敛速度快、精度高的优点。SSA算法简单且有效，实验仿真结果表明，SSA的性能优于目前流行的优化算法。本文将SSA算法与SVM相结合。用松鼠搜索算法优化支持向量机的参数，提高支持向量机的分类精度。

1 液体火箭发动机故障诊断方法及智能优化算法介绍

1.1 液体火箭发动机故障诊断方法介绍

2020年国防科技大学的吴建军等总结了液体火箭发动机故障诊断方法[15]。根据所使用信息类型的不同，将其分为3类：基于模型驱动的方法、基于数据驱动的方法和基于人工智能的方法。

1.1.1 基于模型驱动的方法

基于模型驱动的故障检测与诊断方法，主要包括基于解析模型的方法和基于定性模型的方法。

基于解析模型的方法，其基本原理是以解析方程将系统的输入、状态和输出的内在规律表示出来，从而建立的数学模型。

基于定性模型的方法，其基本原理是根据系统组成元件之间的连接建立诊断系统的结构、行为或功能上的定性模型。

1.1.2 基于数据驱动的方法

基于数据驱动的方法主要是根据系统的输出与故障之间的联系，分析处理发动机的测量输出信号，以此判断故障是否存在及故障发生的位置。基于数据驱动的方法主要包括统计分析、主成分分析、独立分量分析、小波分析和羽流光谱分析、最小领域方法、支持向量机和聚类方法等。

1.1.3 基于人工智能的方法

基于人工智能的方法主要包括专家系统、人工神经网络和模糊理论等方法。

综上，相较于基于模型驱动方法建立复杂精确的数学模型困难重重或计算成本巨大难以实现，基于数据驱动的方法和基于人工智能的方法将研究对象作为黑箱处理，计算简单，容易实现。

考虑到新一代大推力液体火箭发动机具有关键部件多且大多处于高温、高压、强振动的极致环境中，建立合理精确的数学模型是个困难的问题。因此本文选择智能优化算法与基于数据驱动的方法中的支持向量机作为液体火箭发动机故障诊断的分析方法。

1.2 松鼠搜索算法(SSA)

松鼠搜索算法是一种新的自然启发优化范算法，由M.Jain、V.singh、A.Rani于2018年提出[16]。

在松鼠的搜索过程中，有以下4个必要假设：假设1，落叶林中有n只松鼠和相同数量的树，松鼠均匀分布在每棵树上。假设2，每只松鼠都有一种动态的觅食行为，它们各自寻找食物，并优化利用现有的食物资源。假设3，森林里只有3种树，山核桃有最好的食物来源(山核桃坚果)，橡子树有一般的食物来源(橡子坚果)。假设4，认为森林只存在4颗拥有食物资源的树，其中包括3颗橡树(即算法寻求的次优解)和1颗山核桃树(即算法寻求的最优解)，普通树没有食物资源。其中dg是松鼠在树间跳跃的滑行距离，R1、R2、R2是[0,1]范围内的随机数。FSht、FSat、FSnt分别是松鼠到达山核桃树、橡树和普通树的位置。t是迭代次数。Gc是数学模型中的滑动常数，经过严格分析，其值设为1.9。Pdp表示捕猎者存在概率，如果R的值大于捕猎者存在概率，松鼠是安全的。如果小于，则有被捕食的风险，松鼠进行随机行走[17]。

1)当松鼠由橡树向山核桃树移动时位置更新如下：

(1)

2)当松鼠由普通树向橡树移动时位置更新如下：

(2)

3)当松鼠由普通树向山核桃树移动时位置更新：

(3)

不同季节的气温会影响松鼠觅食的活跃程度。该算法中提出了季节性监测条件，有助于算法跳出局部最优。

4)计算季节变量Sc

(4)

(5)

其中:t为当前迭代次数，tm是最大迭代次数。Smin为影响算法的勘探和开发能力。

(6)

莱维分布(Levy distribution)有助于更高效的空间探索。

(7)

其中:ra和rb是[0,1]区间上的符合正态分布的随机数。β是小于2的正常数，σ计算公式如下：

(8)

7)松鼠在山核桃树的位置即最终的最优解。SSA算法流程图如图1所示：

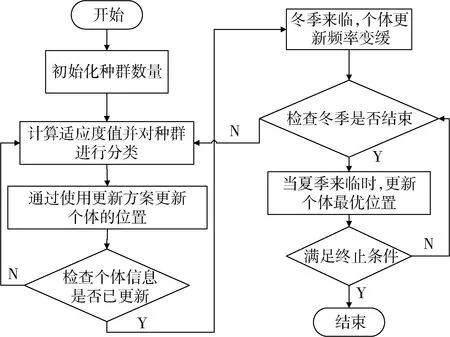
图1 SSA算法流程图

1.3 支持向量机(SVM)

SVM 最早在1963年提出，现在用的SVM是1993年提出，并在1995年发表的版本。支持向量机是比较成熟的分类算法之一。它在分类问题中具有良好的性能。与KNN和多层感知器等其它传统分类算法相比，SVM的计算复杂度更低。近年来，随着大数据时代的到来，深度学习已成为研究热点。SVM在机器学习中，被认为是深度学习问世前性能最优的算法。与深度学习相比，SVM仍具有一定的竞争力。支持向量机最大的特点是它不是黑箱方法，具有坚定的数学理论基础，而且SVM还有参数较少，易于调整的优点[19]。

标准支持向量机使用线性回归来拟合训练数据，假设训练集是：

S={(xi,yi)|i=1,2…,n}，xi是输入，yi是输出，n是样本数。回归函数为：

f(x)=ωTx+b

(9)

其中:ω是权向量，b是偏差。ω和b是通过求解最优问题得到的：

(10)

上述公式需满足以下条件：

(11)

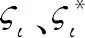
表1 常用核函数表

核函数首先可以通过先验知识选取。如图像分类，一般采用高斯径向基核函数。其次，可以在尝试不同类型的核函数之后，再按照结果准确度判断。本文将根据先验知识，选择RBF作为核函数。

利用拉格朗日方程组可以把优化问题转换为二次规划问题，转换式(12)和(13)：

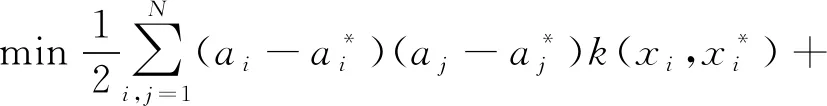
(12)

s.t.

(13)

得到基于核函数的SVM回归方程为：

(14)

惩罚因子(c)和核函数参数(g)是支持向量机的2个重要参数，这2个参数的选择对分类结果有很大影响。

SVM结构如图2所示：

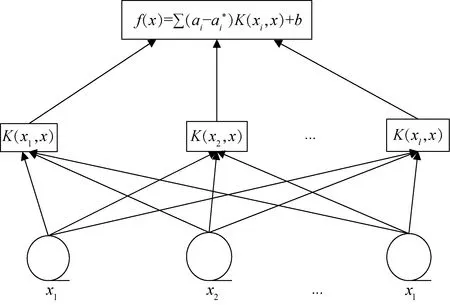
图2 支持向量机结构图

2 SSA-SVM模型构建及其在火箭动力系统的故障诊断实验仿真

2.1 SSA-SVM诊断模型

采用SSA算法优化支持向量机，SSA-SVM模型建立过程如图3所示，具体执行流程如下：

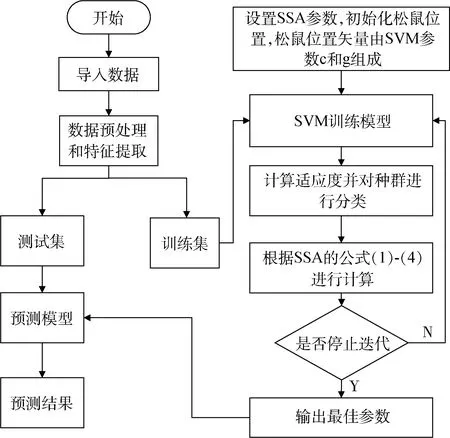
图3 SSA-SVM诊断流程

(1)导入数据，对数据进行预处理，将数据分为测试集和数据集两组；

(2)将支持向量机中核函数参数和惩罚因子作为松鼠搜索算法的位置向量，设置松鼠搜索算法参数，初始化松鼠种群与位置参数；

(3)确定支持向量机模型，并设置参数；

(4)计算松鼠个体适应度，并对种群进行分类；

(5)根据式(1)、(2)、(3)和(4)更新松鼠个体位置；

(6)更新松鼠适应度与最大迭代次数，判断是否达到终止条件。如果达到，则执行下一步，否则返回第3步；

(7)输出最佳参数，建立预测模型；

(8)执行预测模型，得到最佳分类结果。

2.2 训练样本的选取

本次实验输入数据来自于表2的部分监测参数，利用某型号液体火箭动力系统846组数据进行仿真实验，采用MATLAB R2016a作为仿真软件。846组数据分别为6种故障类型，每种类型的数据集数量相同。分别取各类型的113组数据作为训练集，28组数据作为测试集。输出1，2，3，4，5，6分别代表以下故障类型：涡轮泵端面密封泄露、热燃气集合器传递管破裂、波纹管失效、冷却夹套堵塞、涡轮叶片损坏、液管路受损泄露。

表2 动力系统参数检测表

算法参数设置如下：松鼠种群数为10，最大迭代次数为100，滑动常数Gc=1.9，捕食者存在概率Pdp=0.1。在给定参数条件下，运行得到最优核函数参数与惩罚因子，结果分别为：g=0.6469，c=3.8295。

2.3 仿真结果对比

对SVM、经过粒子群算法优化的SVM(PSO-SVM)、经过松鼠搜索算法优化的SVM(SSA-SVM)进行仿真结果对比。

SSA-SVM的误差分布图如图4所示：

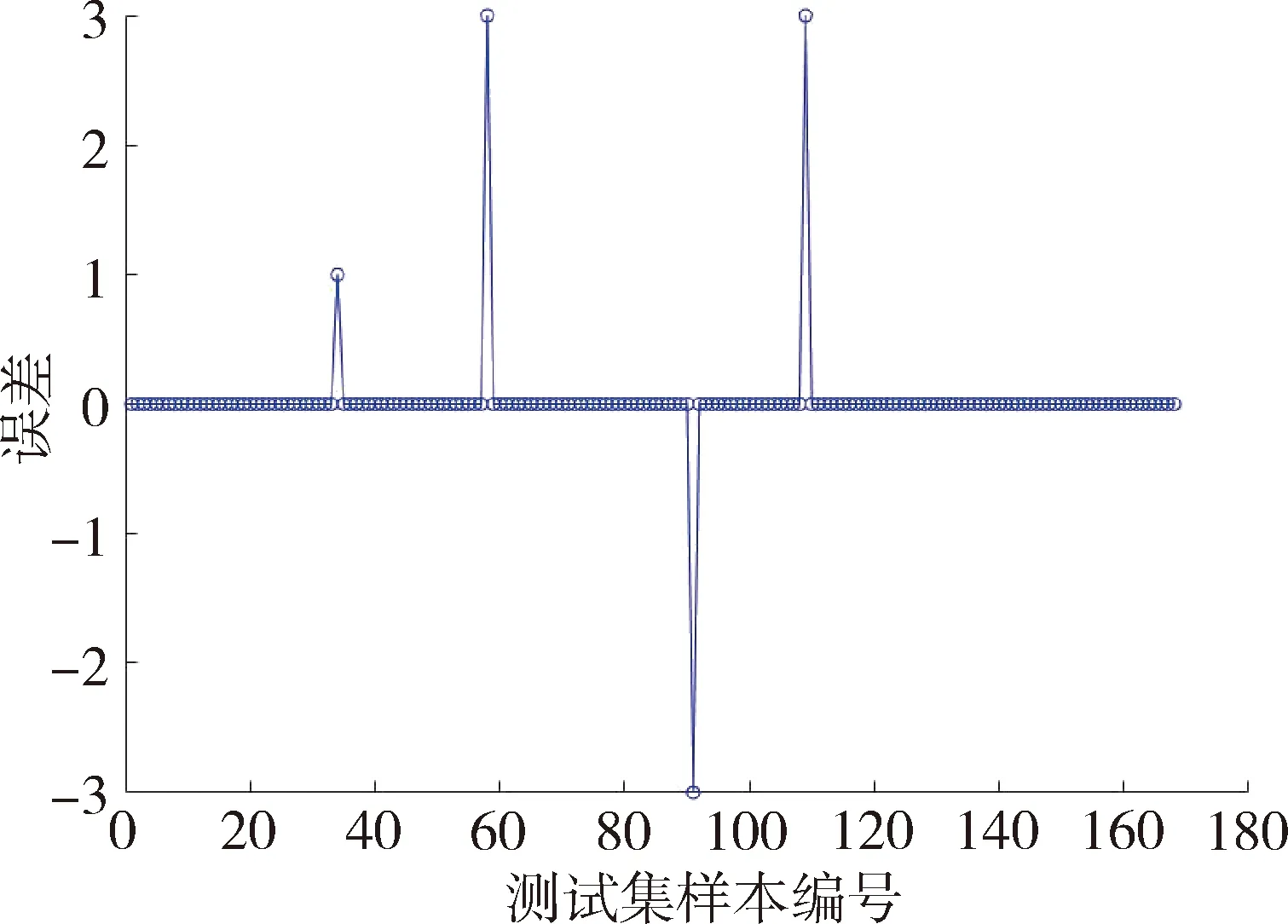
图4 SSA-SVM模型误差分布

由图4可知，利用SSA-SVM模型对测试集进行分类，分类错误个数为4个。为增加SSA-SVM模型可信度，本文将SSA-SVM模型与SVM模型和PSO-SVM模型的结果进行了对比。对比模型PSO-SVM误差分布如图5所示：

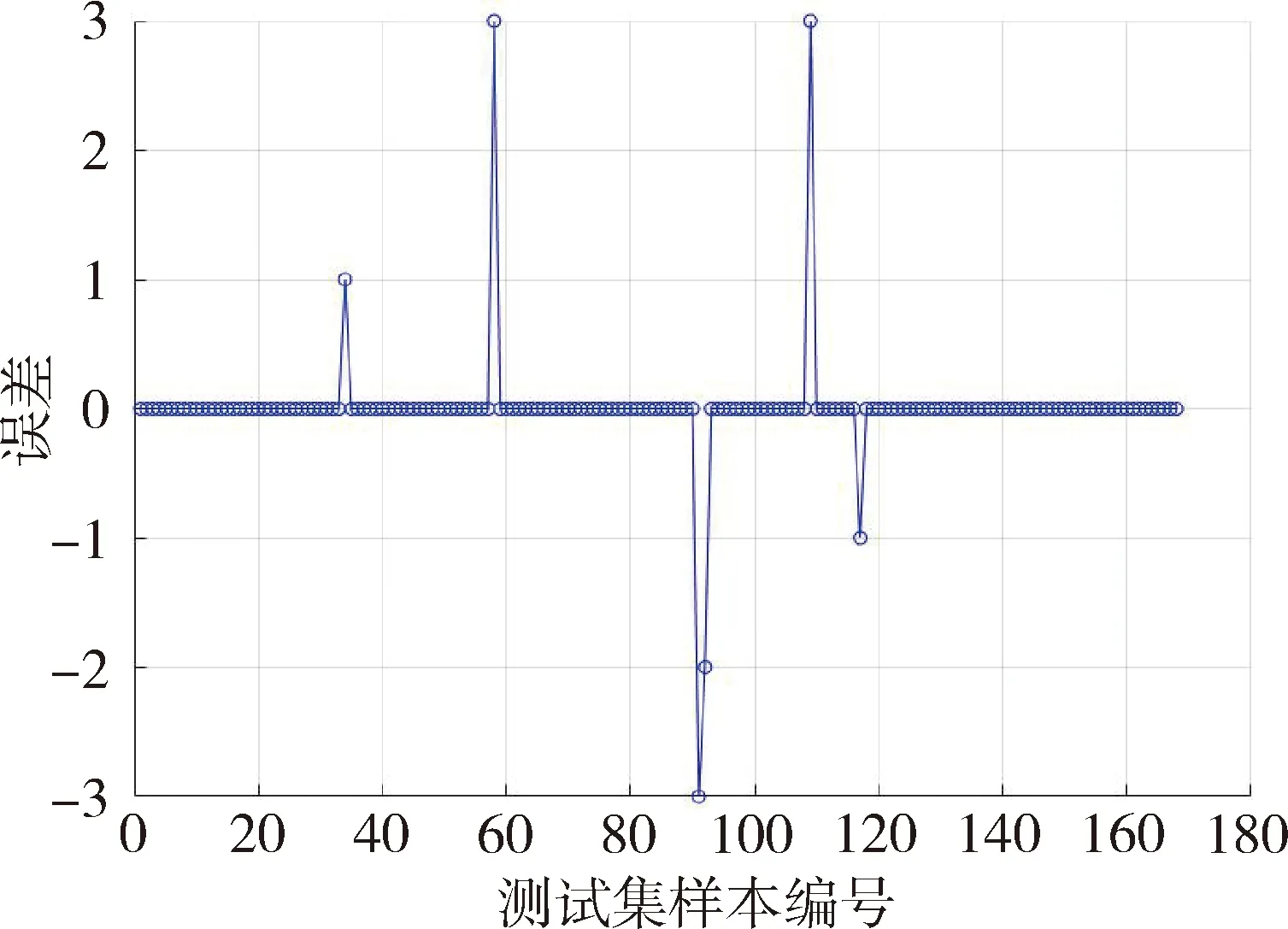
图5 PSO-SVM模型误差分布图

由图5可知，PSO-SVM模型预测误差增加为6个，分类效果低于SSA-SVM模型。SVM的误差分布如图6所示。

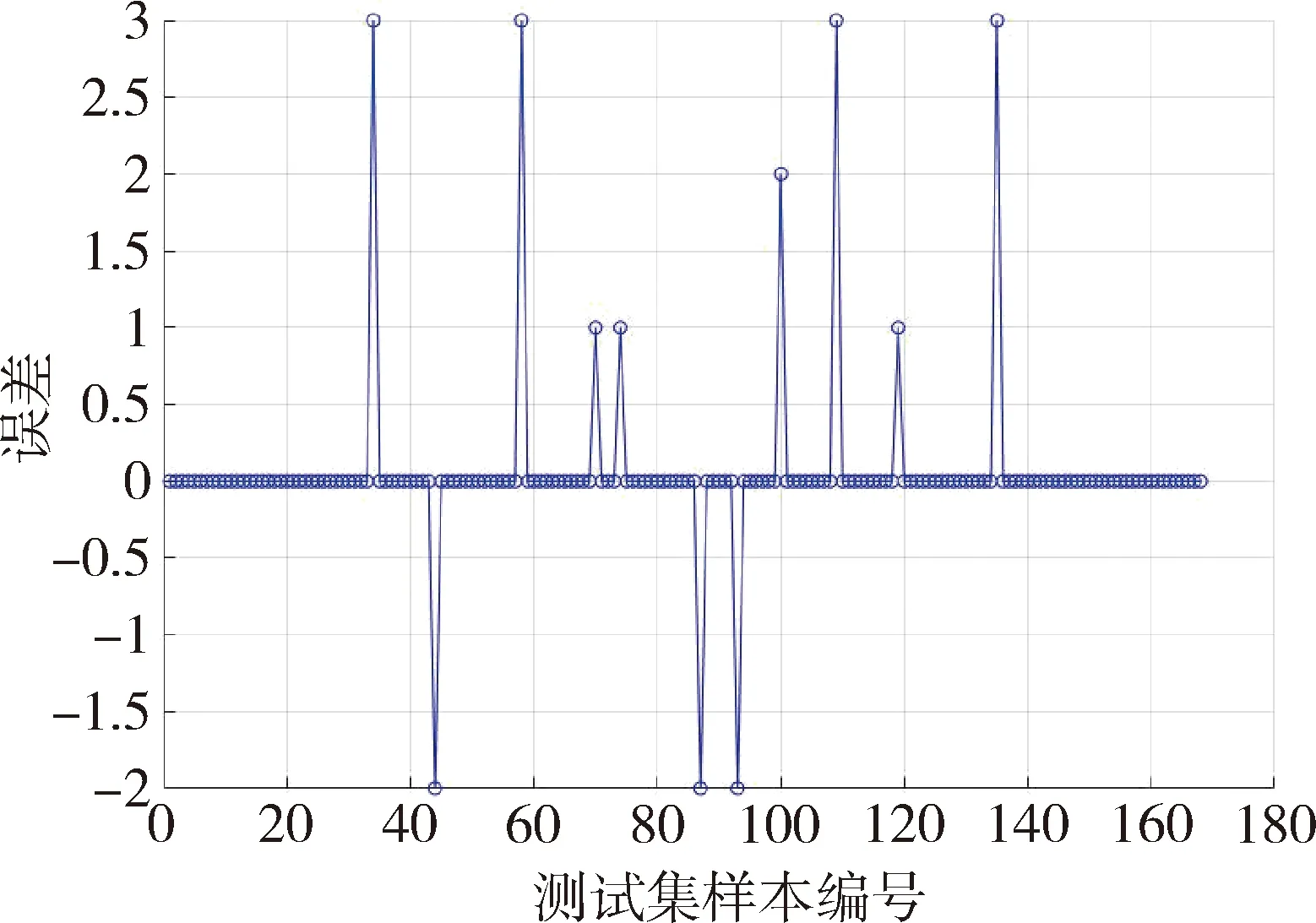
图6 SVM模型误差分布图

由图6可明显看出，单纯的SVM模型分类错误率远远大于PSO-SVM与SSA-SVM模型。

综上所述，由图4～6可知，在168个测试集中SVM模型分类错误个数为11个。PSO-SVM模型的分类错误个数为6个，而基于SSA-SVM模型的液体火箭动力系统的故障诊断错误个数为4个。张伟星[20]等使用BP神经网络进行故障检测的误差率为0.025。4种模型误差对比如表3所示，SSA-SVM模型的测试集的分类错误率降低到0.0238。说明本模型在液体火箭动力系统故障诊断中有较高的准确率，可以应用在液体火箭动力系统的故障诊断中。