一种微型航天器姿态跟踪的四元数实现方法

冯路明 路坤锋 刘晓东

1.北京航天自动控制研究所，北京 100854 2.宇航智能控制技术国家级重点实验室，北京 100854

0 引言

空间航天器在执行对目标跟踪与观测、编队飞行、空间交会对接、轨道转移等空间任务时，需要航天器姿态控制系统精确地跟踪指令坐标系。姿态控制系统的设计效果对在轨服务性能的稳定性和可靠性有着十分重要的影响[1]，因此姿态控制系统研究一直是空间科学和技术领域的一个热点问题。

航天器执行任务期间需要从初始姿态过渡到指令姿态并实现姿态指令的稳定跟踪，描述飞行器的姿态运动通常采用欧拉角法和四元数法。由于航天器姿态机动范围大，当采用欧拉角法时，欧拉方程将出现奇异点。而四元数微分方程是代数方程，在计算过程中不会出现奇异点的情况，因此本文采用四元数描述航天器姿态运动及姿态跟踪方法。

目前姿态跟踪控制器设计方法通常有LQR控制、滑模变结构非线性控制以及自适应控制方法。LQR基于姿态运动的线性化模型，通过最小化某一性能指标求出控制量，但该方法在实现姿态控制的同时不可避免地带来系统线性化误差。滑模变结构控制虽能有效地抑制外界干扰和系统不确定性，但因其采用三通道控制，不能实现能量最小控制。自适应控制通过设计动态的自适应控制器可以逐渐调整一部分系统参数，适应航天器内部系统参数具有较大不确定性的情况，因此广泛应用在航天器姿态控制问题上[2-3]。

目前，航天器的四元数姿态控制方法研究大多集中在解决姿态控制性能需求方面。本文基于现代控制理论，将复杂的非线性航天器姿态运动模型转化成一个特征结构可以任意配置的线性定常状态空间模型。利用极点配置具有很大自由度的特点，通过极点配置法实现线性定常系统的稳定性，该方法的应用性和自由度都很高，设计灵活。

1 基于误差四元数的姿态机动模型

1.1 航天器姿态跟踪的四元数描述

航天器相对惯性空间以角速度ω1旋转，旋转四元数为qd。设期望坐标系相对惯性空间以角速度ωr旋转，旋转四元数为qr。定义由期望坐标系到航天器坐标系的旋转四元数为误差四元数qe，则[4]：

(1)

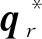
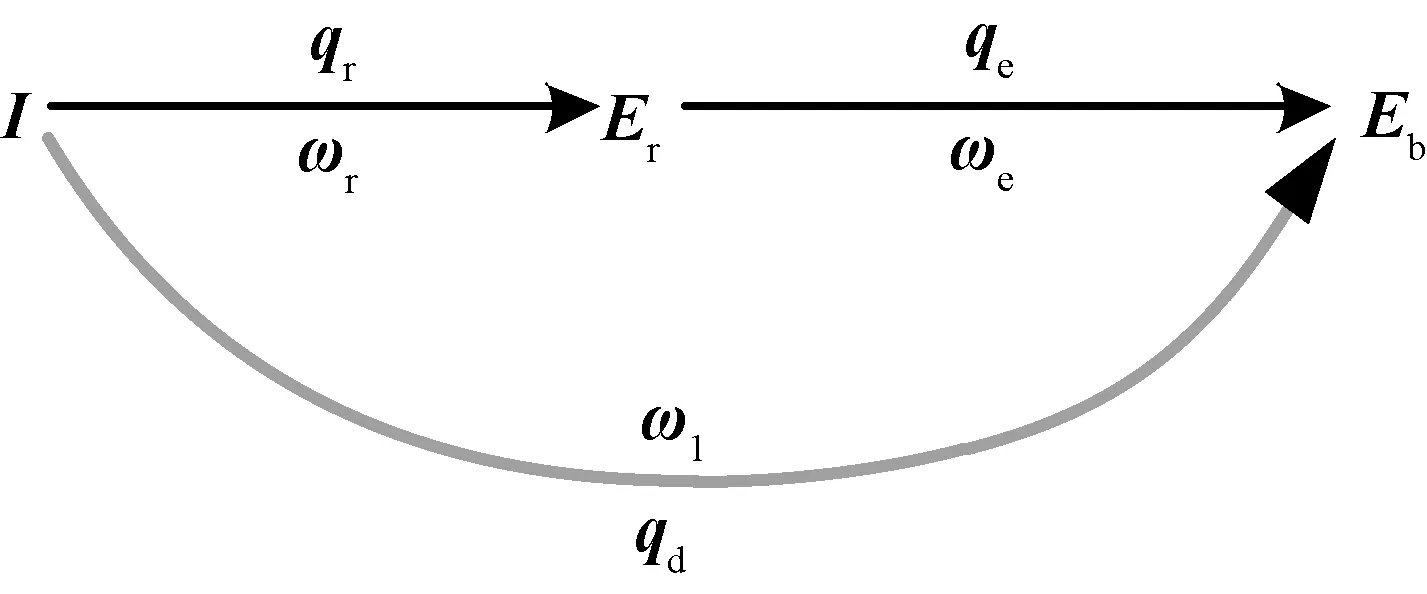
图1 航天器运动四元数与指令四元数关系

航天器姿态运动的四元数微分方程为：

(2)

误差四元数微分方程方程为：

(3)

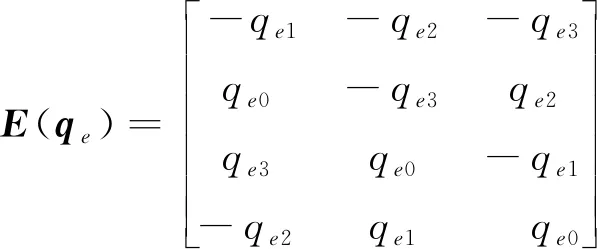
则式(3)可以表示为：

(4)

定义：

(5)

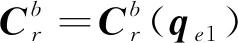
根据刚体运动学理论，航天器姿态运动的动力学方程为：

(6)

(7)

将式(7)代入式(6)，整理可得：

(8)

将式(5)表示的ω1代入式(8)，整理得：

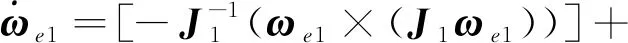
(9)

1.2 基于四元数的姿态跟踪控制系统模型

定义误差四元数矢量部分：q=[qe1qe2qe3]T，由公式(3)可得：

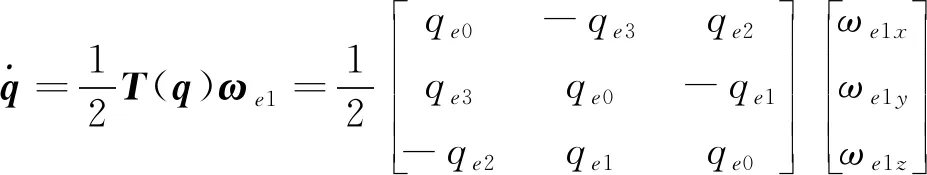
(10)

对公式(10)求导，将一阶的姿态运动学模型转化成姿态动力学模型：

(11)

由式(4)得：

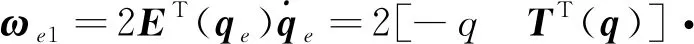
(12)

因此：

(13)

令：

则角速度ωe1可以表示为：

(14)

为了简化推导，假设飞行器各通道之间转动惯量无耦合，即：J1=diag(Jx1，Jy1，Jz1)

令：J=[Jx1Jy1Jz1]T

将ωe1、J1代入式(9)得：

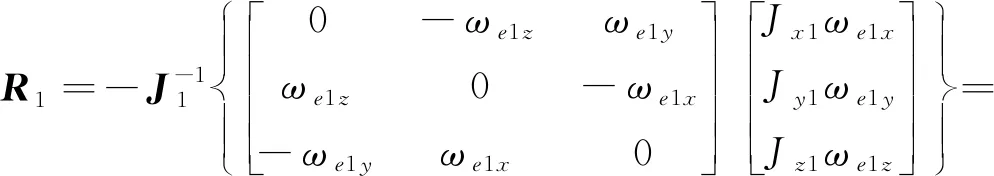
(15)

其中：

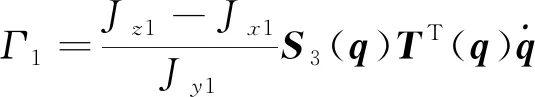
则：

(16)

(17)

(18)

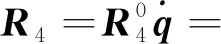
(19)

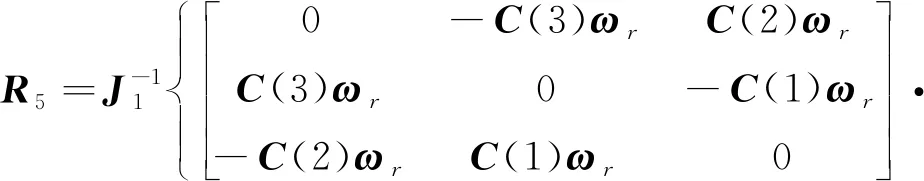
(20)

将式(16)～ (20)代入式(11)，得到由误差四元数描述的姿态控制系统模型：

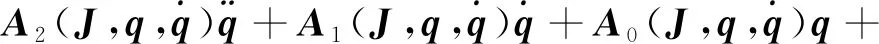
(21)

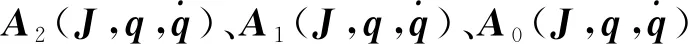
1.3 基于误差四元数的姿态跟踪问题描述

针对式(21)描述的关于q的航天器二阶系统模型，其控制问题的提法是设计适当的控制律u：

u=f(q)=f(q1,q2,q3)

(22)

使得闭环系统

(23)

满足:

(24)

当被控航天器的姿态误差四元数矢量部分q从初始值到达平衡点qe=[0 0 0]T时，控制系统完成了航天器姿态跟踪控制问题。

2 基于误差四元数的姿态跟踪控制器

控制器设计的目的是在系统存在干扰的情况下，实现航天器姿态的稳定与跟踪，因此，对于系统确定性扰动，通过设计补偿控制器来实现姿态控制系统的扰动抑制能力，因此控制器设计如下所述：

u=uf+uc

(25)

其中，uc补偿是为了抑制系统的确定性干扰设计的补偿控制器，uf为状态反馈控制律。

2.1 扰动补偿控制器

将式(25)设计的控制器代入式(21)描述的闭环系统，当选择

即：

(26)

2.2 控制器设计

经过扰动补偿后，控制系统的二阶模型可以表示为：

(27)

状态反馈控制量：

(28)

扰动补偿后的闭环控制系统模型变为：

(29)

其中：

对式(29)表示的系统进行线性变换[5]：

(30)

其中：

则式(28)和式(29)系统的求解问题，可以转化为式(31)描述的Sylvester方程求解问题：

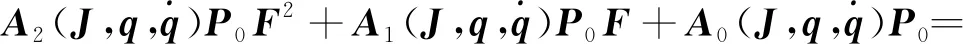
(31)

其中：

式(31)系统左右互质分解及其解为[6-7]：

(32)

Z∈Rn×2n是自由参数，可根据具体的指标进行优化求解。

F∈R2n×2n是自由的待定参数，用于配置系统特征根，可以根据系统指标进行优化求解。

2.3 控制量优化求解

由于式(31)描述的稳定系统系数矩阵F可以自由配置，因此可以通过优化某一特定的性能指标Jopt求解状态反馈控制器uf。

对于线性系统，通常以系统特征根灵敏度作为优化指标[8-9]，因此选择系统特征根的二范数作为优化指标，即：

(33)

式(33)的优化问题，可以通过式(32)描述的带约束非线性规划方法求解：

minJopt(F,Z)

(34)

利用Matlab优化工具箱进行求解，可以得到λi，则

F=diag(λ1,λ2,…,λ2n)

优化出F、Z后，即可求解状态反馈增益矩阵Kf，进而根据确定性扰动与状态反馈控制量求解出系统的控制律：

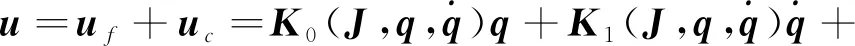
(35)

将u代入式(6)，即可实现航天器姿态跟踪的闭环控制。

3 仿真验证

3.1 仿真条件

假设微型航天器初始时刻处于空间静止状态，指令坐标系以角速度ωr旋转。

(36)

描述指令坐标系的四元数初值：

qr(0)=[0.5000 -0.6456 0.4655 0.3412]T

描述飞行器本体坐标系的四元数初值：

qd(0)=[1.0 0.0 0.0 0.0]T

误差四元数初值为：

[0.5000 0.6456 -0.4655 -0.3412]T

在机动过程中，假设航天器的惯量矩阵不变，且各轴之间无交联耦合。

Jx1=0.014kg·m2
Jy1=0.025kg·m2
Jz1=0.018kg·m2

通过极点配置后的闭环系统矩阵为：

F=diag(-0.18，-0.2，-0.22，-0.35，-0.44，-0.5)

仿真时间150s，控制周期20ms。

3.2 仿真结果

依据3.1节仿真条件进行仿真，结果如下所示：

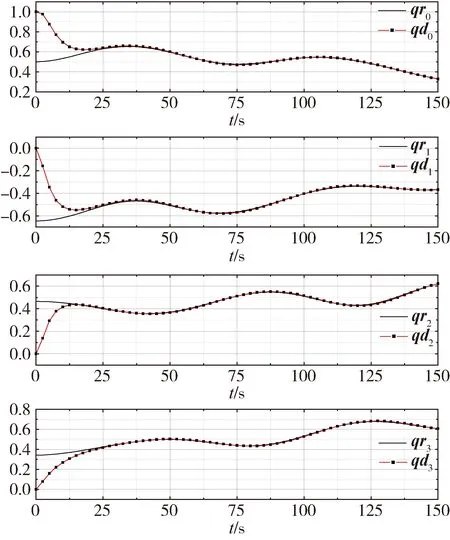
图2 qd与qr随时间变化曲线

图3 误差四元数标量q0随时间变化曲线

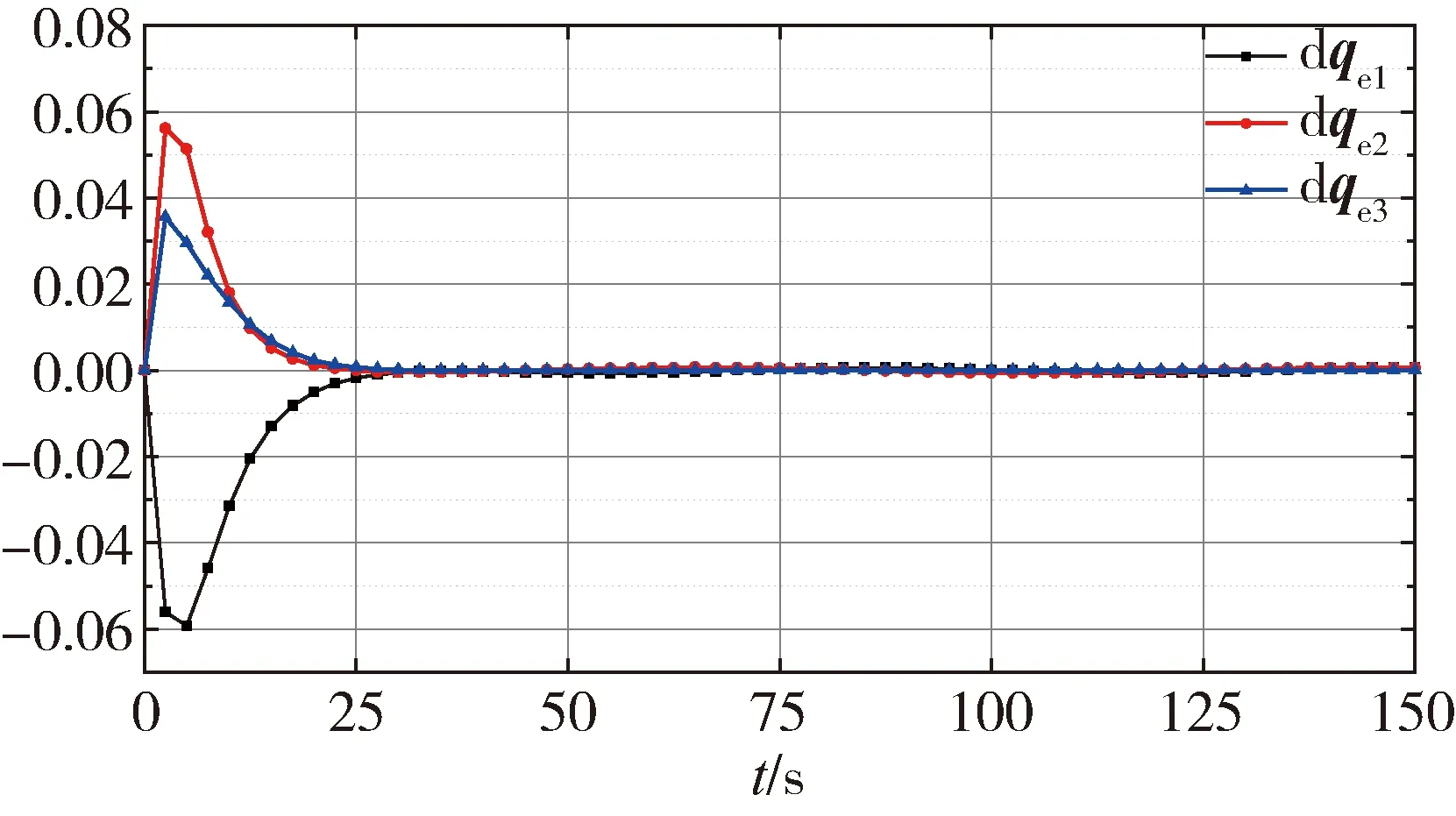
图5 误差四元数矢量导数随时间变化曲线

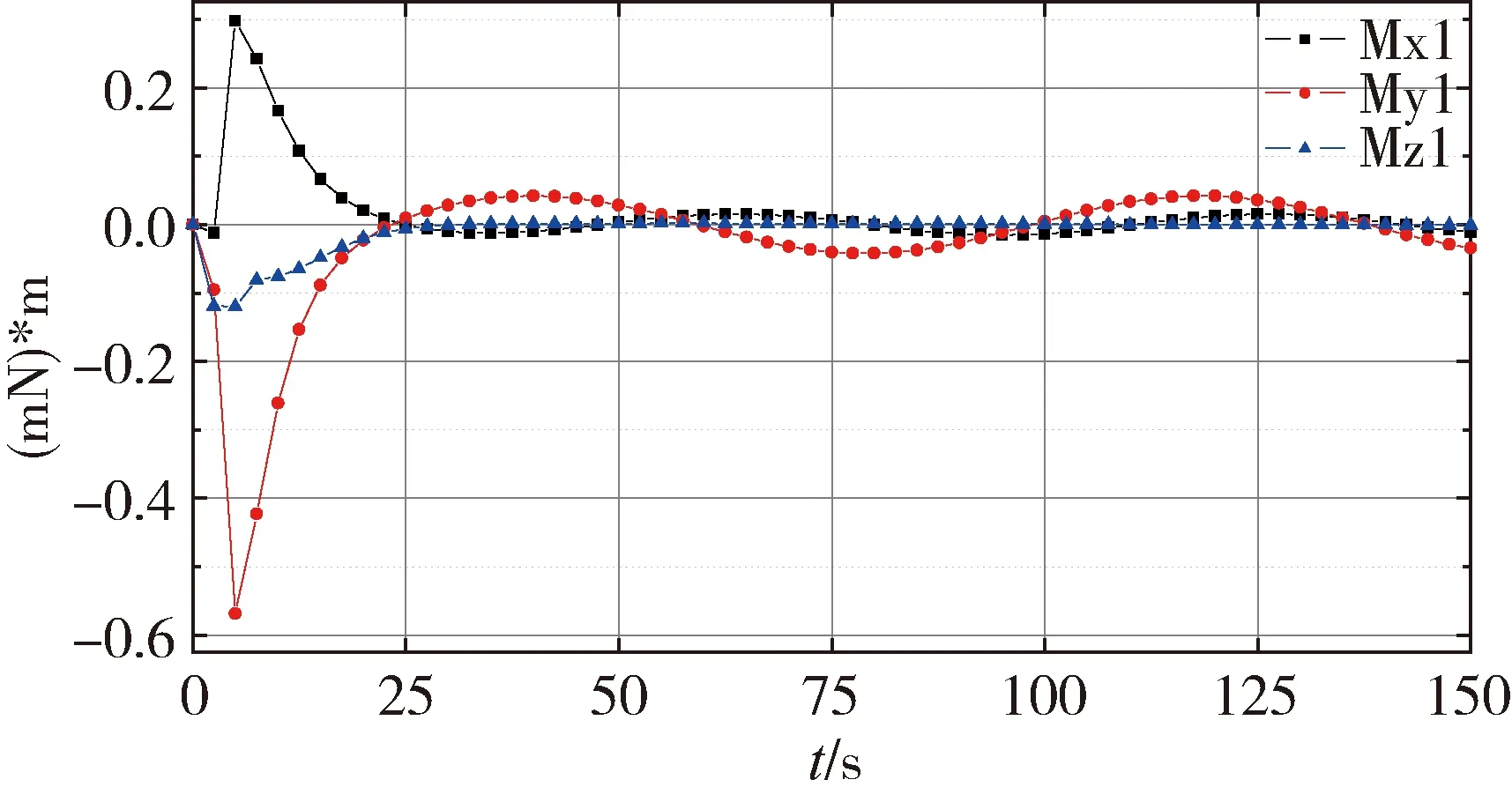
图6 控制力矩随时间变化曲线

4 结论

建立了基于误差四元数的微型航天器姿态控制系统该模型，同时基于状态反馈控制器，通过配置系统的极点，满足飞行器对姿态控制系统的性能需求。数学仿真验证表明：通过四元数状态反馈设计的控制器能够稳定地以高精度跟踪姿态指令。