过驱动卫星姿态动态控制分配研究

谢方圆 张爱民

1. 中国人民解放军63766部队，西双版纳 666200 2. 西安交通大学电子与信息学部，西安 710049

0 引言

卫星运行在复杂多变的太空环境中，不仅面临来自外界的各类干扰影响，还可能由于外界或内部的原因出现各种故障，进而对功能造成影响。在卫星在轨期间的各类故障中，执行机构发生故障的比例很高，而且对卫星姿态造成的影响很大。为了提高卫星对执行机构故障的容错能力，现代卫星往往采用3个以上的反作用飞轮构成冗余执行机构。那么一个控制需求会有多种可行的执行机构分配方案，这就引出了控制分配问题。

针对过驱动卫星的控制分配问题，传统的伪逆分配法，其本质上是固定分配，不能充分利用执行器冗余的优势[1]。动态控制分配(Dynamic Control Allocation, DAC)在故障时根据约束条件和最优化目标将虚拟控制力矩重新进行分配，使执行机构最终输出的控制力矩尽可能与虚拟控制力矩一致[2]。提高了控制过程的精确度、系统对执行机构故障的容错能力，进而延长卫星在轨寿命。如文献[3]中针对空天飞行器再入过程异类冗余执行机构的复合控制分配问题，设计了基于二次规划的按需动态分配律，实现了姿态准确跟踪。文献[4]在过驱动卫星姿态控制中应用基于负载均衡的控制分配方法，优化了推力分配布局，延长了执行机构使用寿命。

相对于被动容错方法，采用DAC可以无需设计过于复杂的控制器，以提供对飞轮故障的鲁棒性，而是通过DAC方法进行处理；相对于主动容错方法，不需要重构控制器[5]，也会相应的使控制方法的设计复杂度降低。所以，将简单的控制器和DAC结合，是针对飞轮故障的一种有效的姿态控制设计方法。但在以往的文献中，应用动态控制分配方法时，将权值矩阵对角线元素设置为最大限幅值倒数，并没有将飞轮故障的影响考虑在内。本文考虑飞轮故障，重新设计了对角权值矩阵的计算方法。

另外，无论何种执行机构，都存在由于物理限制存在输出力矩和转速的上限。在要求的力矩或转速超过上限时，执行机构就无法跟随控制命令，造成实际输出的力矩和要求之间存在误差，即执行机构发生了饱和。但一些文献在设计控制律时并没有考虑这一点。如文献[6]中，仅设计了控制器，对于工程实践中可能出现的执行机构饱和问题没有加以考虑，缺乏实践指导意义。Kenneth提出了解决这一问题的两种方法[7]。其中利用控制效率矩阵(安装矩阵)零空间特性的修正方法，可以使超出执行机构位置和速度限制的分配方案重新落入可行域内，且保证控制矢量方向不变。

卫星发射过程中，颠簸可能带来结构变形，现代快速响应卫星安装矩阵在发射前可能来不及校准，这些因素都会使卫星不可避免的存在执行机构安装偏差，往往会对控制精度有较大影响。所以高精度的姿态控制必须考虑执行机构存在安装偏差的问题[8-9]。

以上提及的卫星姿态控制中可能出现的问题，以往许多文献中一般只着眼于它们中的一部分，而忽略了其他部分，没有综合考虑。虽然设计的控制方法对其他未考虑的问题可能有一定的控制效果，但缺乏理论支撑和仿真验证。也有少量的文献将以上问题综合考虑[10]，但控制器设计过程复杂，不利于实际工程应用。

本文综合考虑不确定干扰、飞轮安装偏差、故障以及饱和，结合滑模控制和动态控制分配，利用零空间法处理飞轮的饱和问题。仿真结果证明，本文提出的控制方法对上述问题有良好的控制效果。

1 卫星姿态模型

1.1 卫星姿态方程

采用四元数描述的卫星姿态动力与运动学方程为：

(1)

(2)

(3)

式中：J∈R3为卫星惯量矩阵；we表示本体系Β相对于期望系Ο的误差角速度；有

(4)

(5)

假设1.干扰力矩d有界，即满足‖d‖≤λ。其中:‖·‖表示(·)的2-范数，λ>0为正常数。

假设2.角速度w和姿态四元数qv均可通过直接测量或间接计算得到。

1.2 飞轮结构与故障分析

1.2.1 飞轮安装偏差分析

记执行机构的数量为m>3，执行机构产生的力矩向量为v=[v1v2…vm]T。卫星的控制力矩u=[u1u2…un]T(n=3)，由反作用飞轮通过安装矩阵D提供：

un×1=Dn×mvm×1

(6)

考虑航天器反作用飞轮存在安装偏差ΔD,设标称部分为D0,即有：

D=D0+ΔD

(7)

1.2.2 飞轮故障分析

飞轮效率矩阵为F=diag(f1,f2,…,fm),其中fi(i=1,2,…,m)∈[0,1]表示每个飞轮的故障系数，fi=1表示飞轮正常，fi∈(0,1)表示飞轮效率降低，fi=0表示完全失效。记vc为飞轮的输入指令。飞轮实际输出v的表达式如下：

v=Fvc

(8)

假设4.F已经准确检测或估计到，其估计误差本文不做讨论。

1.2.3 飞轮饱和分析

定义飞轮在物理限制下可以输出控制力矩的范围为：vmin≤v≤vmax，速度的范围为：ηmin≤η≤ηmax。设采样时间为T,综上，在某一时刻t飞轮输出力矩范围可表示为：

(9)

(10)

这使得位置和速率的双重约束转化为单位计算周期内的位置约束问题。

1.3 问题陈述

综上，本文研究的问题可以描述为：在卫星姿态控制过程中，考虑存在不确定干扰以及飞轮安装偏差的情况下，当飞轮出现故障以及饱和时，设计怎样的控制方案，能使卫星姿态系统仍能稳定运行。

2 控制器设计与稳定性分析

首先考虑在卫星存在不确定干扰和飞轮安装偏差的情况下如何设计控制律u，使系统渐近稳定。

如果使用伪逆法将控制力矩分配到各个飞轮，则：

(11)

式中：u∈R3为控制模块计算得到的所需的控制力矩。将式(6)、(7)和(11)代入式(3)中可得：

(12)

设计滑模变量s=we+βe，可得：

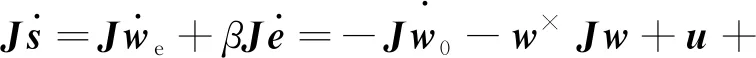
(13)

定义

(14)

则

(15)

设计Lyapunov函数

(16)

则

(17)

设计控制律

u=-A-ksgn(s)-kss

(18)

式中:k、ks为待确定的正常数。代入式(17)中：

(19)

式中:sTksgn(s)=k‖s‖，代入式(19)可得

(20)

由假设1和假设3可知

(21)

将控制律代入可得

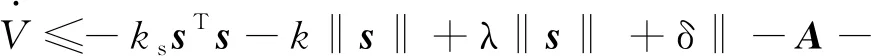
(22)

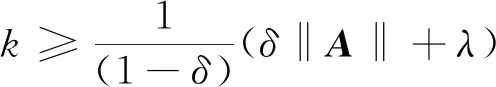
(23)

控制律中的ks和滑模矢量参数β的取值如下：

(24)

ts为要求的响应时间，根据控制任务需求选取。值得一提的是，在滑模控制的实际应用中，由于惯性、滞后等因素的存在，会不可避免的产生抖振。使用边界层法，即用饱和函数sat(s)代替符号函数(开关函数)sgn(s)，可以达到削弱抖振的目的，并提高仿真速率。这里取饱和函数为：

(25)

并令ε=0.001。

3 动态控制分配策略

从前面的分析可知，仅仅使用伪逆法进行力矩分配是无法应对飞轮故障的。所以这里使用动态控制分配处理飞轮故障。

3.1 优化目标

动态控制分配问题本质上是一个优化问题，求解它是一个数学规划问题。选择l2范数作为优化目标：

(26)

s.t.

(27)

式中:v(t)∈Rm为所求的飞轮力矩指令，vs(t)∈Rm为期望的稳态飞轮力矩，v(t-T)∈Rm是上一时刻的飞轮力矩指令，W1和W2为对角权值矩阵；u(t)∈Rn为虚拟控制力矩，D0∈Rn×m是安装矩阵的标称部分，Ω表示飞轮控制力矩的可行域。

文献[11]中将W1矩阵对角线元素设置为最大限幅值倒数，但这种方法并没有将飞轮故障的影响考虑在内。事实上，当星上故障检测系统已经发现某飞轮存在故障，则应增大W1对应的对角线值，使分配时尽量减少使用该飞轮。根据这两个方面的要求，本文将文献中的方法加以改进，将W1对角线元素设置为：

(28)

3.2 求解

在不考虑饱和影响的情况下，优化问题变为：

(29)

s.t.

D0v(t)=u(t)

(30)

根据文献[12]，可得优化问题的解为：

v(t)=Evs(t)+Fv(t-T)+Gu(t)

(31)

(32)

4 零空间法

采用零空间法处理飞轮饱和。

安装矩阵D∈Rn×m，存在一组m-n个m维正交向量，它们构成了Rm上D的零空间的一组基。将这组向量组成的矩阵记为N∈Rm×(m-n)，即满足DN=0，则DNx=0,∀x∈Rm-n，记vm=Nx。向量vp满足Dvp=u，则向量v=vp+vm有下式成立：

u=Dv=D(vp+vm)=Dvp+DNx+
Dvp+0·x=Dvp=u

(33)

式(33)说明若初始解vp加上一个由D的零空间基组成的向量vm，等式仍成立。所以，基于零空间控制分配方法就应用了这一思路：给定了初始解vp，满足Dvp=u，在vp∉Ω时，寻找x，使得v=vp+vm=vp+Nx∈Ω成立。

若经过计算后得到的v满足了所有分量未超出约束范围，则将修正结果输出到执行机构，若还存在超出约束范围的分量，则重复以上的修正过程。值得注意的是，以上方法存在多次迭代仍不能使所有分量都落入约束范围内的情况，这时需要设定一个最大迭代次数，若仍有超出约束范围的分量，就将其置于极限值后停止修正，这时输出的执行机构命令虽然无法合成要求的控制量，但避免了多次迭代浪费宝贵的控制时间。

5 仿真校验

5.1 仿真实验

设卫星的转动惯量矩阵：

J0=diag(6.292,9.650,5.477)kg·m2

(34)

设系统初始姿态角为θ0=[10 10 10]o或θ0=[45 45 45]o两种值。

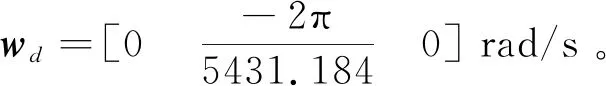
考虑4个反作用飞轮按照αi=35.25°,βi=45°(i=1,2,3,4)的标称安装角安装于卫星上。则由文献[13]可知

(35)

外干扰在三个通道上均设置为：

uf=0.0005sin(0.1t)N·m

存在安装偏差角Δαi,Δβi。仿真中Δαi(i=1,2,3,4)在[-4.5° 4.5°]之间随机选择，Δβi(i=1,2,3,4)在[-5.5° 5.5°]之间随机选择。

仿真中的飞轮故障设置为某飞轮完全失效,其他飞轮能正常运转，既在仿真中对应的飞轮效率矩阵的对角线元素为0。设置飞轮最大位置限制为±0.25N·m，转速最大限制为0.03N·m/s。取ts=60s。设计以下3种条件：

仿真1：初始姿态角[10° 10° 10°]，未发生饱和，3号飞轮完全失效。仿真结果如图1～2所示。

图1 飞轮指令与实际产生的力矩差

仿真2：初始姿态角[45° 45° 45°]，发生了饱和，飞轮正常。仿真结果如图3所示。

仿真3：初始姿态角[45° 45° 45°]，发生了饱和，且2号飞轮完全失效。仿真结果如图4所示。

图2 虚拟力矩与实际输出力矩差

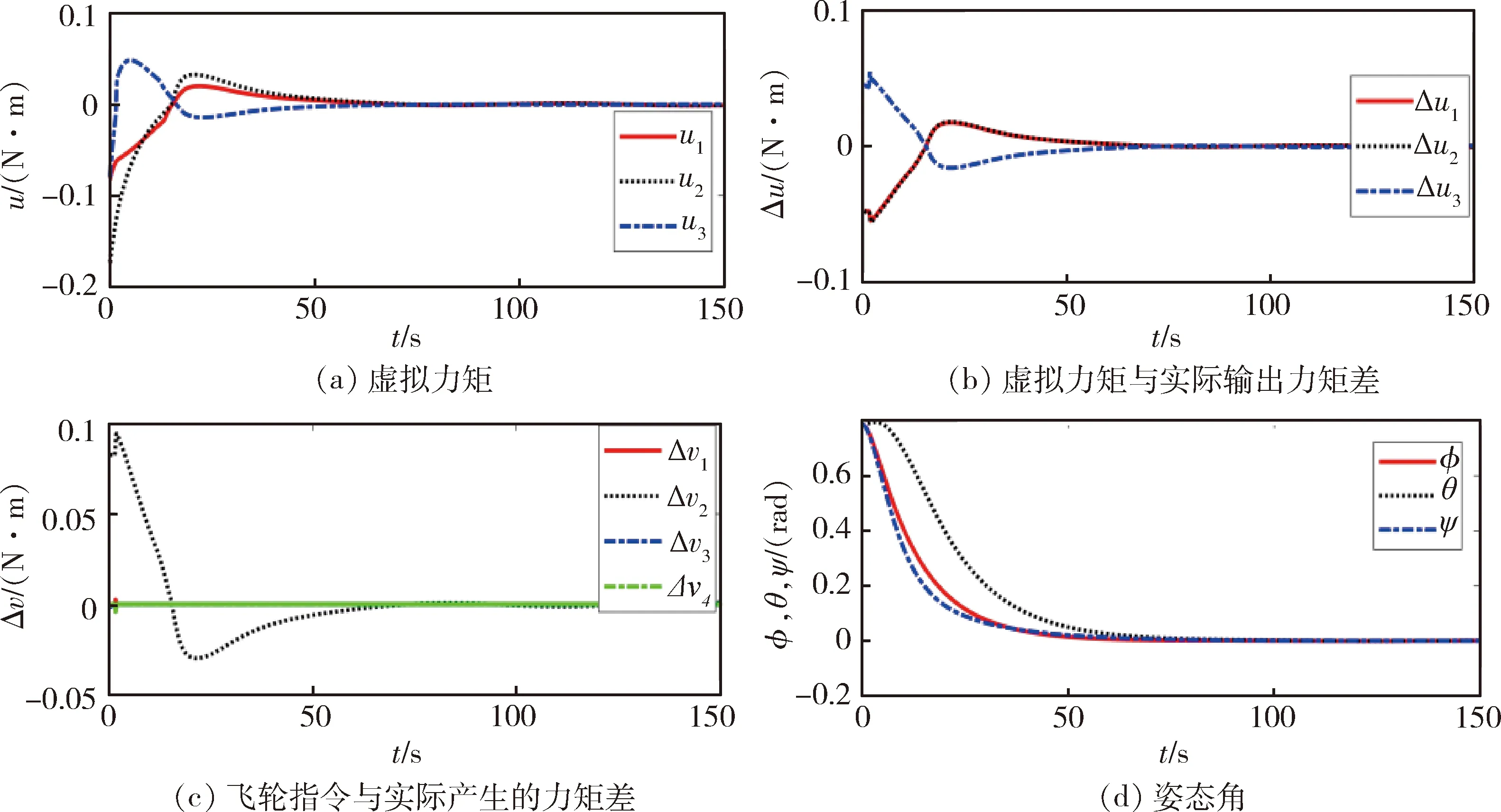
图3 无DAC，无零空间法仿真结果

图4 有DAC，有零空间法仿真结果

5.2 结果分析

通过对比仿真1中的两组实验结果，发现在同样的控制目标下，相对于无DAC时，有DAC时飞轮更好地跟踪了力矩指令，且稳态不存在波动。这是由于无DAC时，违逆法仍然将控制力矩按照安装矩阵的伪逆分配给3号飞轮较大的力矩，但此飞轮无法响应，导致其输出和指令之间的差Δv很大，相应的会造成较大的Δu。有DAC时，失效飞轮对应的W1矩阵对角线元素增大，抑制了向3号飞轮分配较大的力矩，所以，使Δv减小，降低了分配误差。

通过对比仿真2中的两组实验结果，发现有零空间法时，Δu三个分量的绝对值都有所减低，证明了零空间法对饱和影响的抑制作用。这是由于发生饱和时，无零空间法时，超出飞轮限制的力矩会被直接置于饱和值，不做其他处理，造成合成的力矩存在误差;有零空间法时，首先将超出限制的分量置于饱和值，再根据算法计算剩余的分量，循环一定次数，输出调整后的值。相当于将饱和的分量超限部分让剩余未饱和的分量分担，从而降低了控制误差。

在仿真 3中，在干扰、偏差、失效、饱和共同存在时，设计的控制方法仍能有良好的稳态性能，说明了设计的控制律的有效性；对比图3和图4两组实验结果，发现当失效和饱和同时存在时，在DAC和零空间的共同作用下，Δv和Δu都明显降低，使得控制过程得到了改善。所以本文设计的控制方法不仅能使系统最终趋于稳定，还能改善系统的控制过程，有效应对本文中的姿态控制问题。

6 结论

研究了不确定干扰、飞轮安装偏差、故障、饱和同时存在时的卫星姿态控制问题。首先针对卫星姿态在不确定干扰和飞轮存在安装偏差时设计滑模控制律，并验证了其稳定性；而后分别应用动态控制分配和零空间法处理飞轮故障和饱和。最后设计对比仿真，仿真结果与预期一致，证明了设计的控制方法对本文中的姿态控制问题的有效性。并且在降低稳态和动态误差方面都取得了一定的效果。本文设计的控制方法避免了复杂的控制器设计过程，适应性更广，更易于工程应用。